Содержание
- 2. Означення. Випадковою величиною називають величину, яка в результаті випробування набуває одне і тільки одне можливе значення,
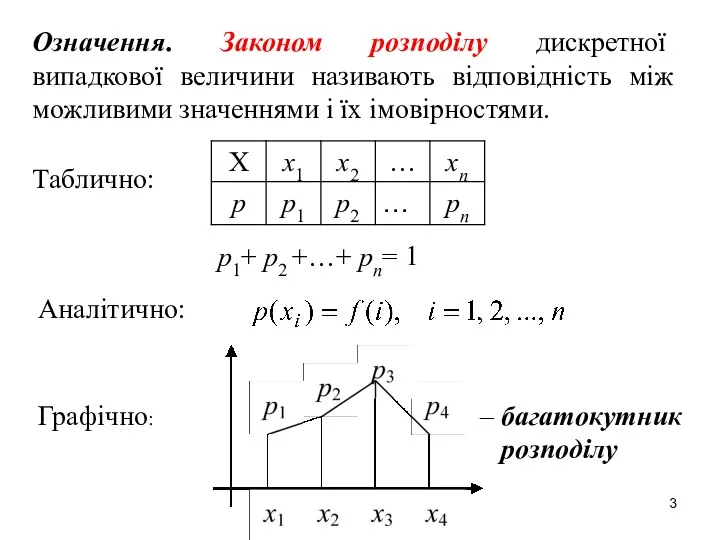
- 3. Означення. Законом розподілу дискретної випадкової величини називають відповідність між можливими значеннями і їх імовірностями. Таблично: Аналітично:
- 4. Означення. Функцією розподілу випадкової величини Х називається функція F(x), що визначає імовірність того, що випадкова величина
- 5. Властивості функції розподілу: 3) 5) Якщо Х – непрерывна випадкова величина, то імовірність того, що вона
- 6. Функцію f(x) називають щільністю імовірності або диференціальною функцією розподілу. Означення. Щільністю розподілу імовірностей неперервної випадкової величини
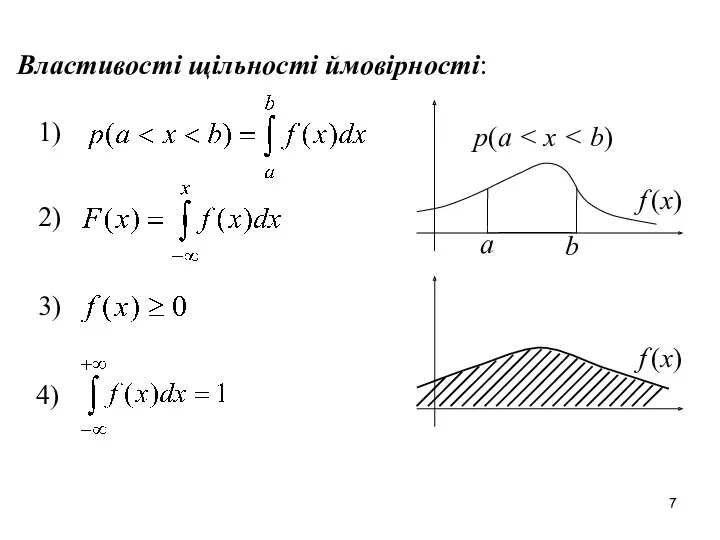
- 7. Властивості щільності ймовірності: a b f (x) p(a f (x)
- 8. Дискретні і неперервні випадкові величини. Дискретна випадкова величина: Неперервна випадкова величина: приймає окремі, ізольовані значення. можливі
- 9. Означення. Математичне сподівання дискретної випадкової величини Х називається сума добутків всіх можливих значень випадкової величина на
- 10. Імовірнісний зміст математичного сподівання: математичне сподівання наближено дорівнює середньому арифметичному значень випадкової величини. Нехай n –
- 12. Властивості математичного сподівання 1. де 2. 3. 4. 5. - тільки для незалежних ВВ ! 6.
- 13. Приклад. , але X і Y сильно відрізняються
- 14. Питання: чи можна оцінити дисперсії можливих значень випадкової величини розрахувавши відхилення кожного з цих значень від
- 16. 1. Дискретна випадкова величина
- 17. 2. Неперервна випадкова величина За означенням Але
- 18. Середнє квадратичне відхилення Означення. Середнім квадратичним відхиленням випадкової величини Х називається корінь з її дисперсії:
- 19. Властивості Середнє квадратичне відхилення 1. , де 2. 3. Дисперсія 1. , де 2. 3. 4.
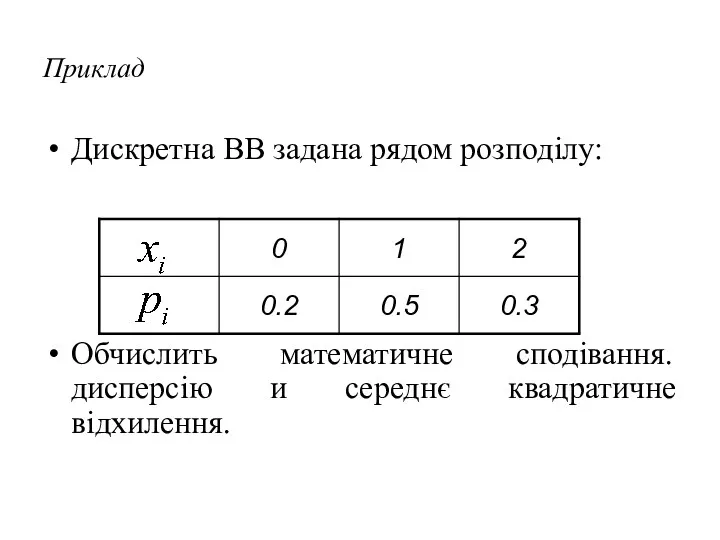
- 20. Приклад Дискретна ВВ задана рядом розподілу: Обчислить математичне сподівання. дисперсію и середнє квадратичне відхилення.
- 21. 1. . 2. . . . 3. .
- 22. Неперервна ВВ задана щільністю імовірності Обчислить математичне сподівання. дисперсію и середнє квадратичне відхилення.
- 23. 1. 2. 3.
- 24. 4. Початковий момент порядку k – дискретна – неперервна Початковий момент першого порядку: – математичне сподівання
- 25. Якщо k = 0, то . Якщо k = 1, то . Якщо k = 2,
- 26. 5. Центральний момент порядку k – дискретна – неперервна Центральний момент другого порядку: – дисперсія
- 27. Якщо k = 0, то ; Якщо k = 1,то ; Якщо k = 2, то
- 28. Вводиться коефіцієнт асиметрії (характеристика скошеності): де – центральний момент 3-го порядку, а – середнє квадратичне відхилення
- 29. Центральний момент 4-го порядку використовується для характеристики положення вершини кривої (крутості кривої) розподілу відносно еталона –
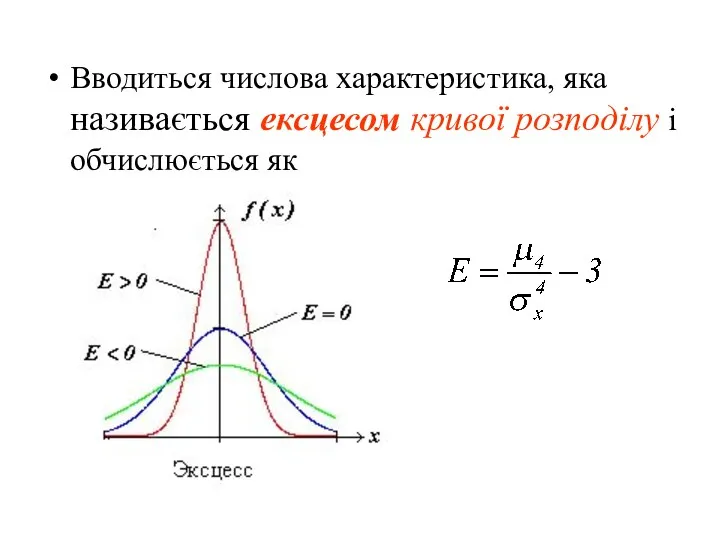
- 30. Вводиться числова характеристика, яка називається ексцесом кривої розподілу і обчислюється як
- 31. 6. Мода Для дискретної випадкової величини мода – це найбільш імовірне значення ВВ. 0,24 0,36 0,20
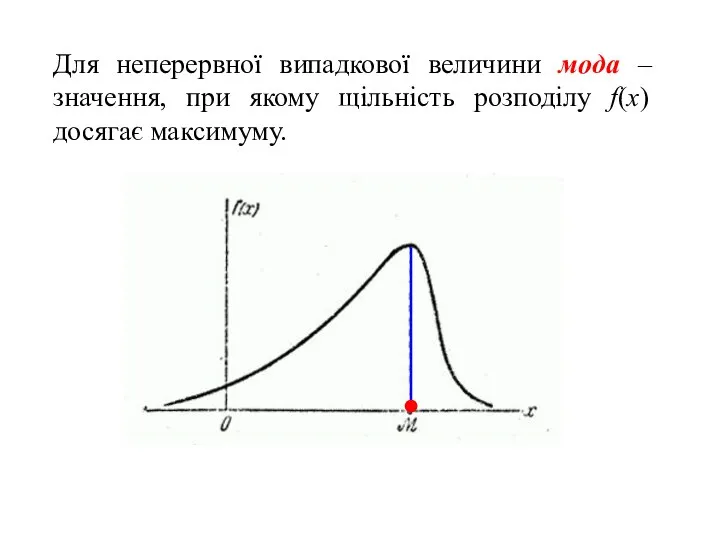
- 32. Для неперервної випадкової величини мода – значення, при якому щільність розподілу f(x) досягає максимуму.
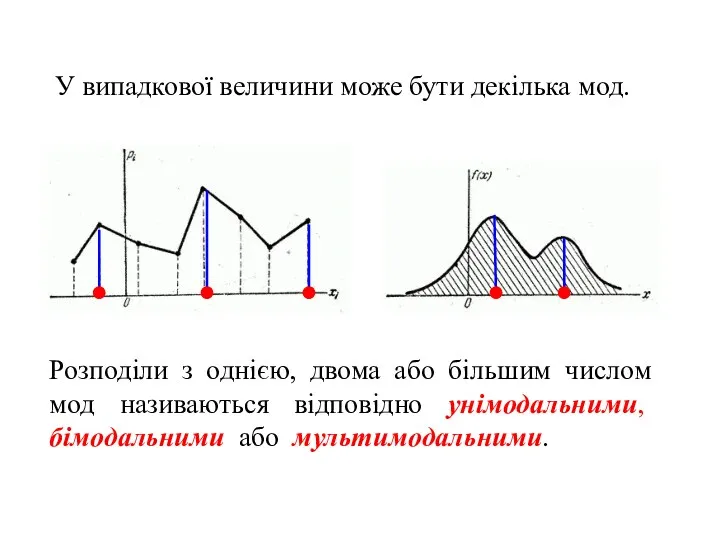
- 33. Розподіли з однією, двома або більшим числом мод називаються відповідно унімодальними, бімодальними або мультимодальними. У випадкової
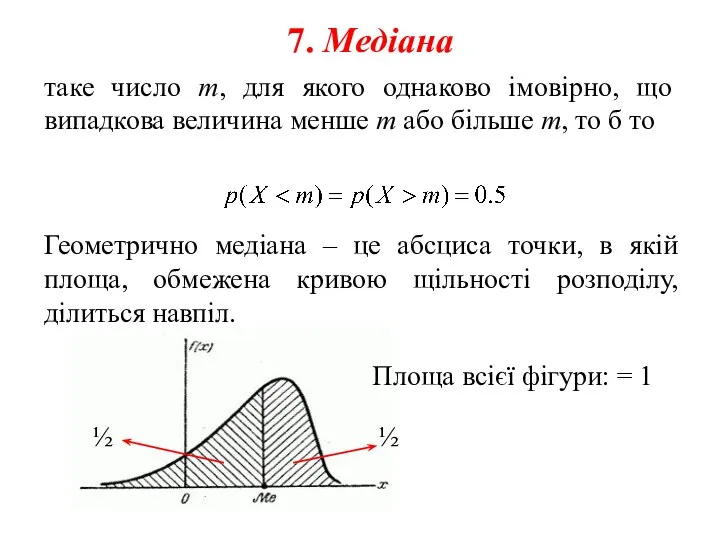
- 34. таке число m, для якого однаково імовірно, що випадкова величина менше m або більше m, то
- 35. 8. Квантіль рівня р F(x) – функція розподілу F-1(x) – функція, обернена до функції розподілу Квантіль
- 36. Основні дискретні розподіли Біноміальний розподіл Розподіл Пуассона Геометричний розподіл Гіпергеометричний розподіл Рівномірний розподіл
- 37. 1. Біноміальний розподіл Х – число появ події А в n незалежних випробуваннях p – імовірність
- 38. 2. Розподіл Пуассона n – дуже велике, p – дуже мале, Можливі значення: k = 0,
- 39. 3. Геометричний розподіл Х – число випробувань, яке необхідно провести до першої появи події А p
- 40. 4. Гіпергеометричний розподіл Х – число стандартних виробів серед відібраних Можливі значення: k = 0, 1,
- 41. 5. Рівномірний розподіл Дискретна випадкова величина має рівномірний розподіл, якщо її функція імовірності на всій області
- 42. Основні неперервні розподіли Рівномірний розподіл Показниковий (експоненціальний) розподіл Нормальний розподіл Розподіл Пірсона Розподіл Стьюдента Розподіл Фішера
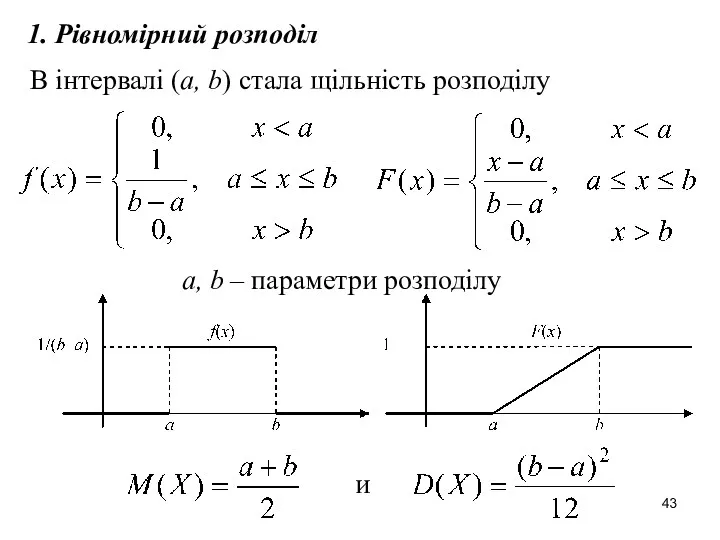
- 43. 1. Рівномірний розподіл В інтервалі (a, b) стала щільність розподілу a, b – параметри розподілу и
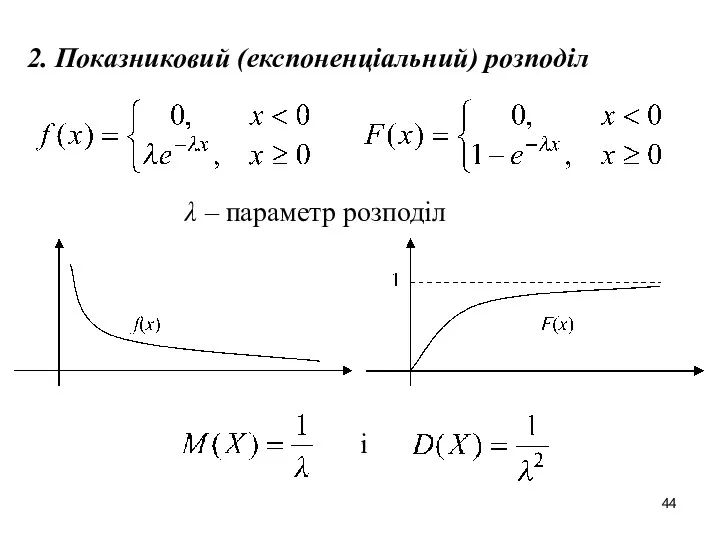
- 44. 2. Показниковий (експоненціальний) розподіл λ – параметр розподіл і
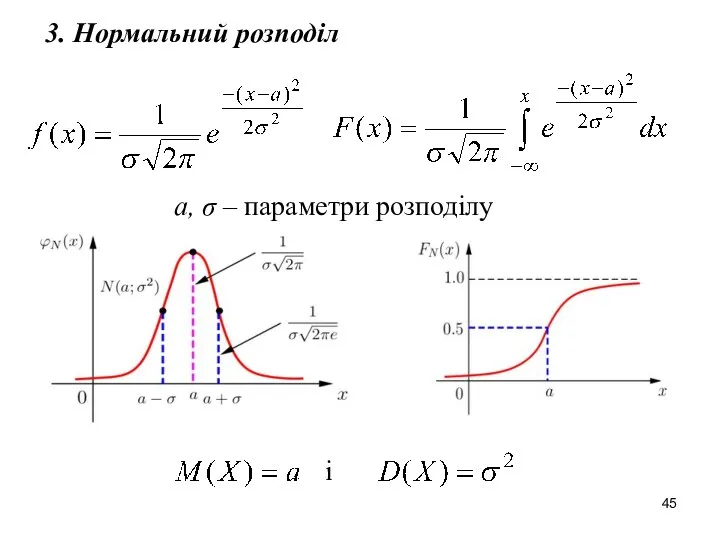
- 45. 3. Нормальний розподіл і a, σ – параметри розподілу
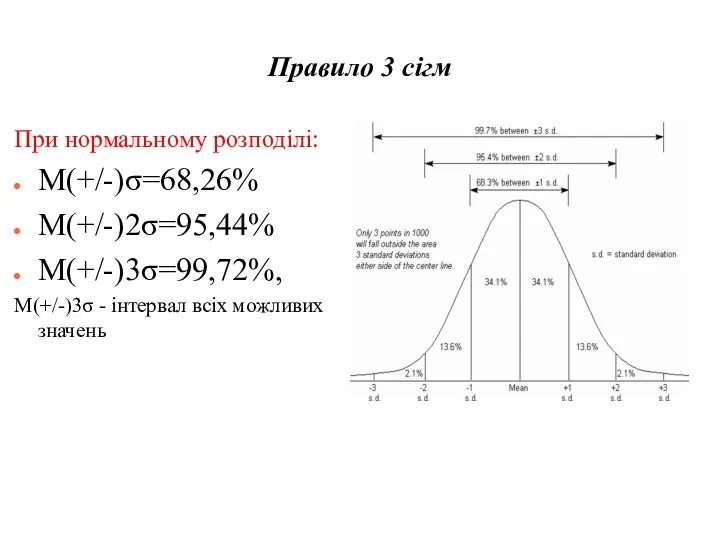
- 47. Правило 3 сігм При нормальному розподілі: M(+/-)σ=68,26% M(+/-)2σ=95,44% M(+/-)3σ=99,72%, M(+/-)3σ - інтервал всіх можливих значень
- 48. Властивості нормального розподілу Правило 3 сігм (99,72% значень лежать в межах M+/-3σ) Розподіл симетричний (А=0), ексцес
- 49. Нехай незалежні випадкові величини Х1, Х2, …, Хk мають нормальний розподіл, до того ж матаматичне сподівання
- 50. 5. Розподіл Стьюдента (t-розподіл) k – параметр розподілу При збільшенні числа ступенів свободи розподіл Стьюдента швидко
- 51. 6. Розподіл Фішера (F-розподіл) k1 і k2 – параметри розподілу Оскільки X ≥ 0 і Y
- 52. Граничні теореми 1. Закон великих чисел. 2. Центральна гранична теорема.
- 54. Теорема Бернуллі. Якщо в кожному з n незалежних випробуваннях імовірність p того, що відбудеться подія A
- 55. Теорема Ляпунова. Якщо випадкова величина X дорівнює сумі великої кількість взаємнонезалежних випадкових величин, усі значення якої
- 58. Скачать презентацию
















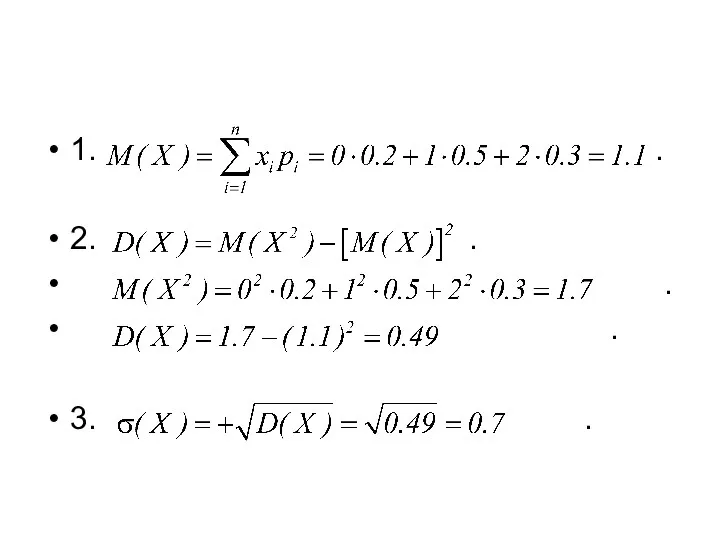

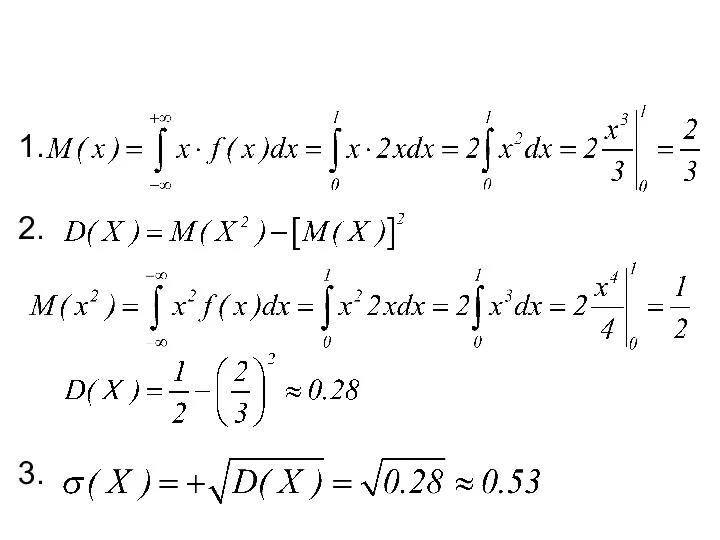



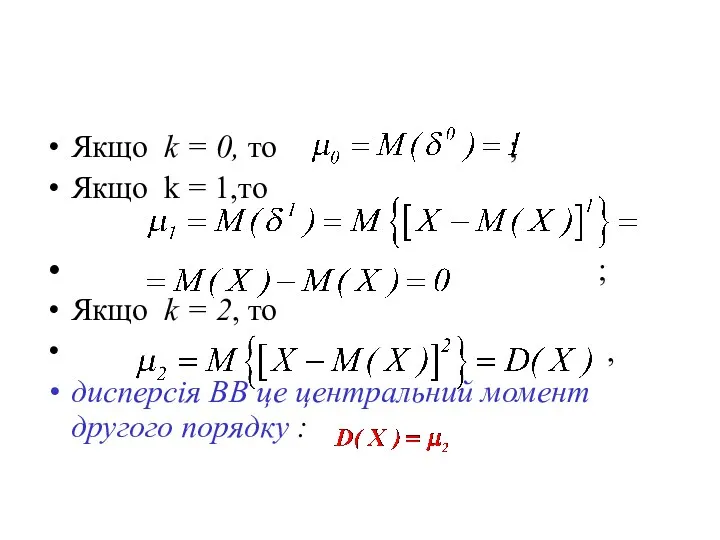





















 Формулы в математике
Формулы в математике Использование игр-головоломок для развития самостоятельности в выборе способов решения в старшем дошкольном возрасте
Использование игр-головоломок для развития самостоятельности в выборе способов решения в старшем дошкольном возрасте Введение в математический анализ
Введение в математический анализ Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Тема 4.1 Нахождение экстремумов функций с одной переменной
Тема 4.1 Нахождение экстремумов функций с одной переменной Число и цифра 5.
Число и цифра 5. Длина окружности. Площадь круга. 6 класс
Длина окружности. Площадь круга. 6 класс Путешествие по океану Математики
Путешествие по океану Математики Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений Перпендикулярные прямые
Перпендикулярные прямые Решение задач в два действия. 1 класс
Решение задач в два действия. 1 класс Закрепление материала
Закрепление материала Текстовые задачи. Теория вероятностей
Текстовые задачи. Теория вероятностей Вычитание из чисел 8 и 9. Состав чисел 8, 9
Вычитание из чисел 8 и 9. Состав чисел 8, 9 Сложение чисел с разными знаками
Сложение чисел с разными знаками Методы экономической статистики и эконометрики (способы стохастического факторного анализа)
Методы экономической статистики и эконометрики (способы стохастического факторного анализа) Задачи на увеличение и уменьшение числа на несколько единиц
Задачи на увеличение и уменьшение числа на несколько единиц Динамическое программирование. (Лекция 3)
Динамическое программирование. (Лекция 3) Действия с обыкновенными дробями. Умножение и деление
Действия с обыкновенными дробями. Умножение и деление Правильный многоугольник
Правильный многоугольник Олимпиада
Олимпиада Математика и космос
Математика и космос таблица умножения и деления, задания тестового характера для интерактивной доски Диск
таблица умножения и деления, задания тестового характера для интерактивной доски Диск Перехід між кутами у правильних пірамідах
Перехід між кутами у правильних пірамідах Свойства функции
Свойства функции Переместительное свойство умножения
Переместительное свойство умножения Переместительное свойство умножения
Переместительное свойство умножения Координатная плоскость. НОД и НОК. 6 класс
Координатная плоскость. НОД и НОК. 6 класс