Содержание
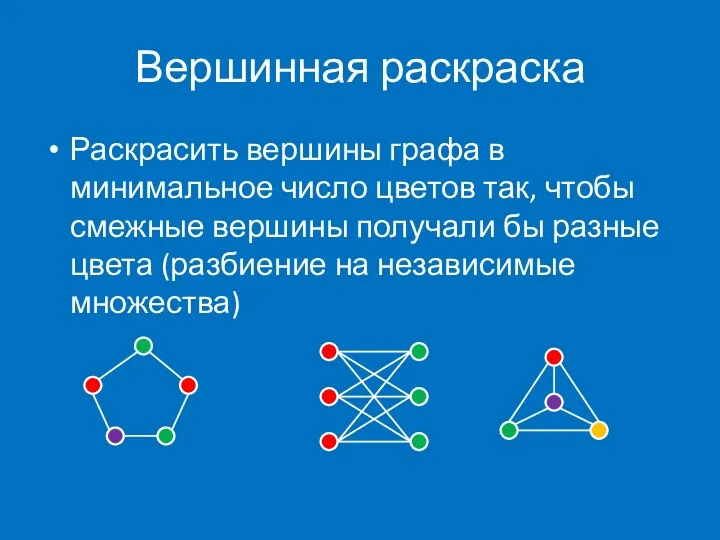
- 2. Вершинная раскраска Раскрасить вершины графа в минимальное число цветов так, чтобы смежные вершины получали бы разные
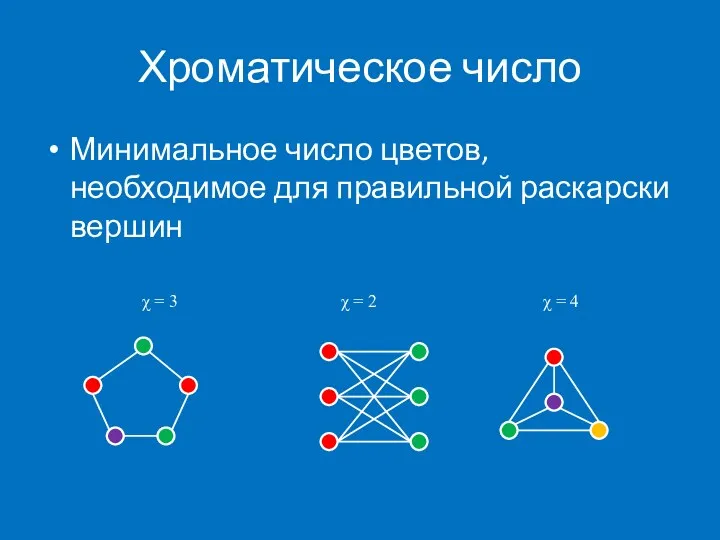
- 3. Хроматическое число Минимальное число цветов, необходимое для правильной раскарски вершин χ = 3 χ = 4
- 4. Нижние оценки для хроматического числа χ ≥ ω, где ω – мощность максимальной клики χ ≥
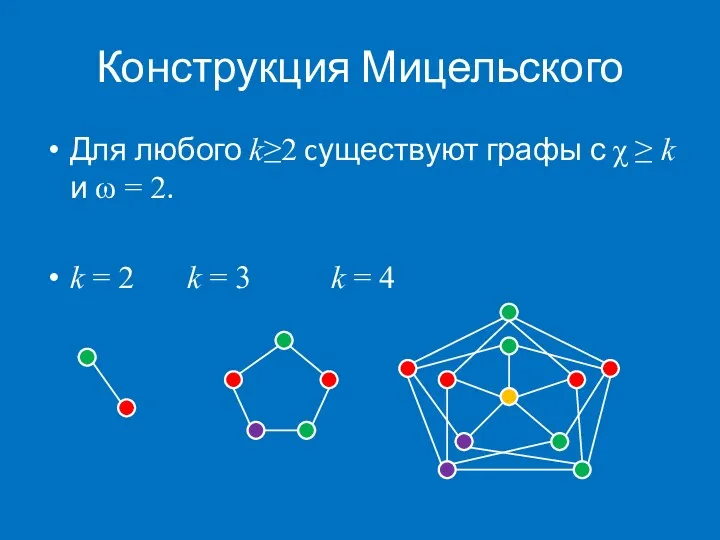
- 5. Конструкция Мицельского Для любого k≥2 cуществуют графы с χ ≥ k и ω = 2. k
- 6. Конструкция Мицельского Граф Mk+1 строится из Mk следующим образом: для каждой вершины v добавим ее копию
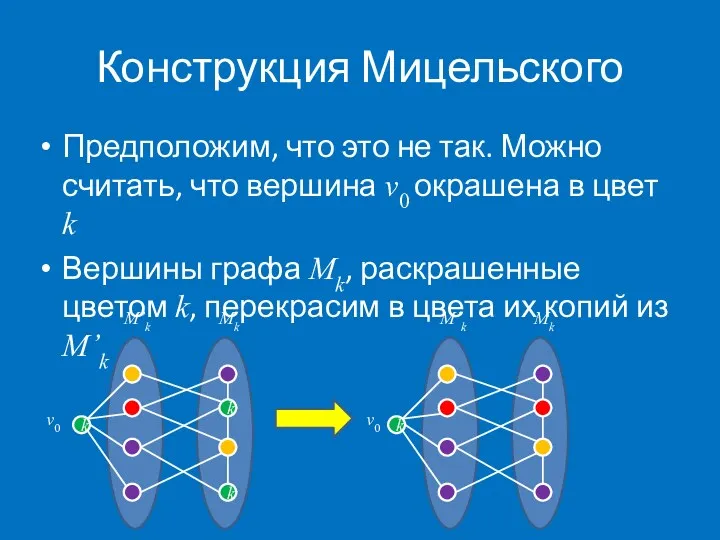
- 7. Конструкция Мицельского Предположим, что это не так. Можно считать, что вершина v0 окрашена в цвет k
- 8. Верхние оценки для хроматического числа Граф называется t-вырожденным, если в любом его подграфе есть вершина степени
- 9. Доказательство Индукция по n: при удалении любой вершины граф остается t-вырожденным Удалим вершину v степени t
- 10. Оценка χ ≤ Δ+1 достигается для нечетных циклов (Δ=2, χ=3) и полных графов (Δ=n–1, χ=n). Теорема
- 11. Доказательство Для Δ≤2 утверждение очевидно. Пусть Δ≥3 Индукция по n. Удалим из G вершину v. Полученный
- 12. Доказательство 1) В любой раскраске графа H все цвета 1,2,…,Δ присутствуют среди цветов соседей вершины v.
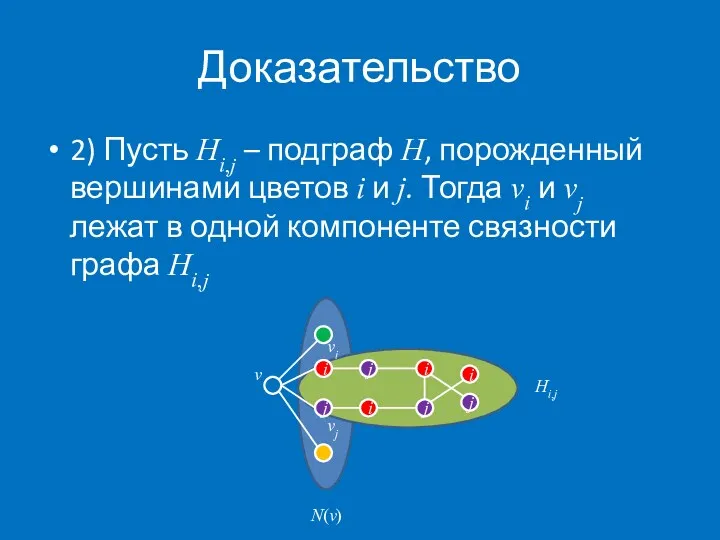
- 13. Доказательство 2) Пусть Hi,j – подграф H, порожденный вершинами цветов i и j. Тогда vi и
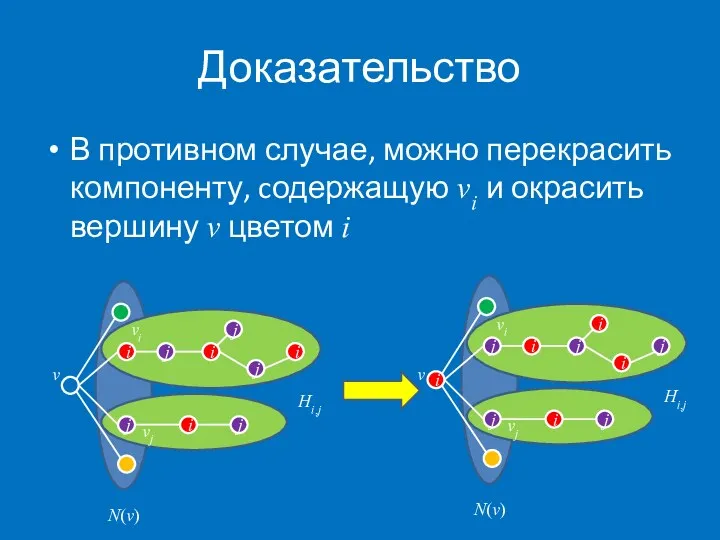
- 14. Доказательство В противном случае, можно перекрасить компоненту, cодержащую vi и окрасить вершину v цветом i j
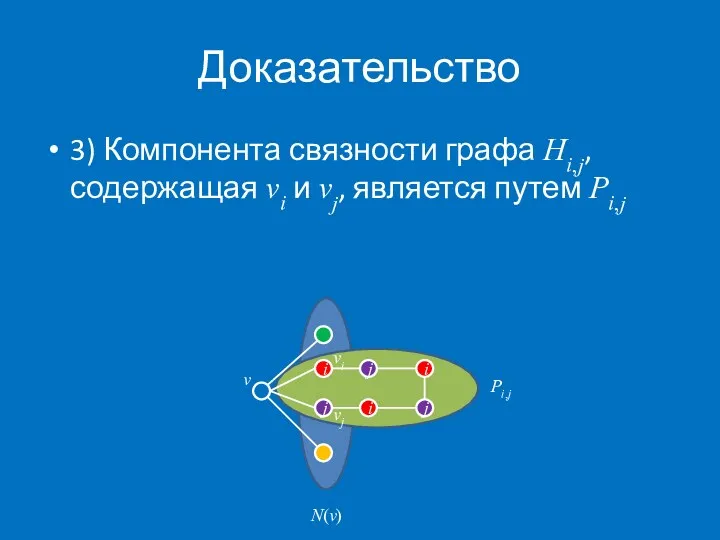
- 15. Доказательство 3) Компонента связности графа Hi,j, содержащая vi и vj, является путем Pi,j j i N(v)
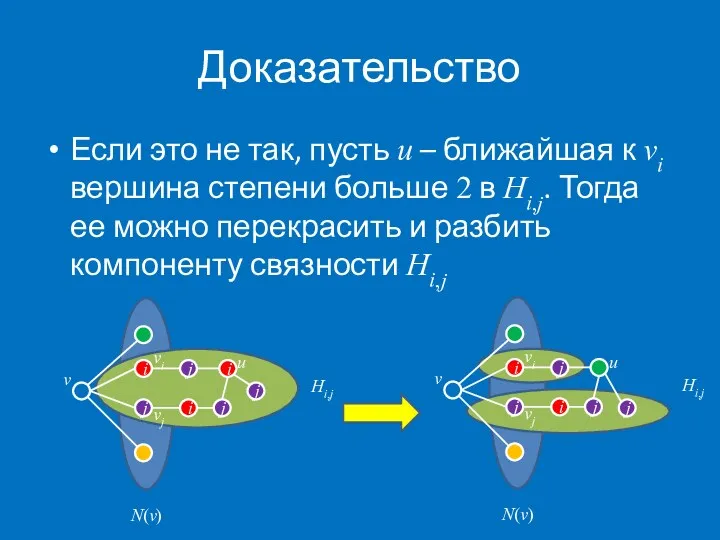
- 16. Доказательство Если это не так, пусть u – ближайшая к vi вершина степени больше 2 в
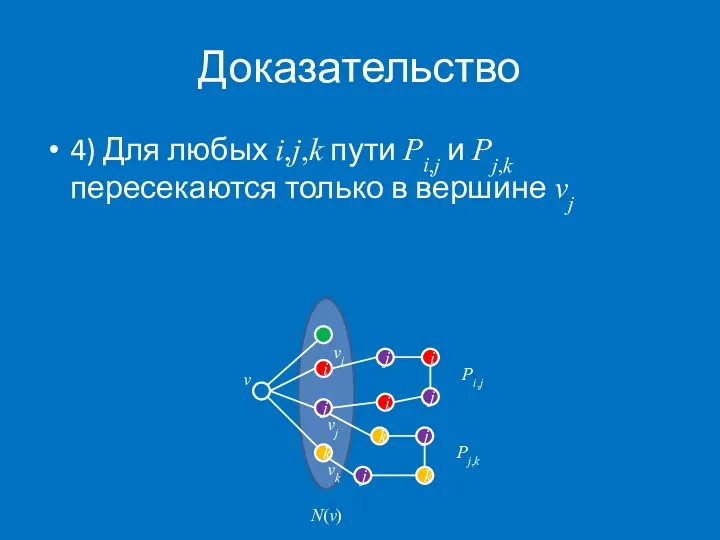
- 17. Доказательство 4) Для любых i,j,k пути Pi,j и Pj,k пересекаются только в вершине vj k j
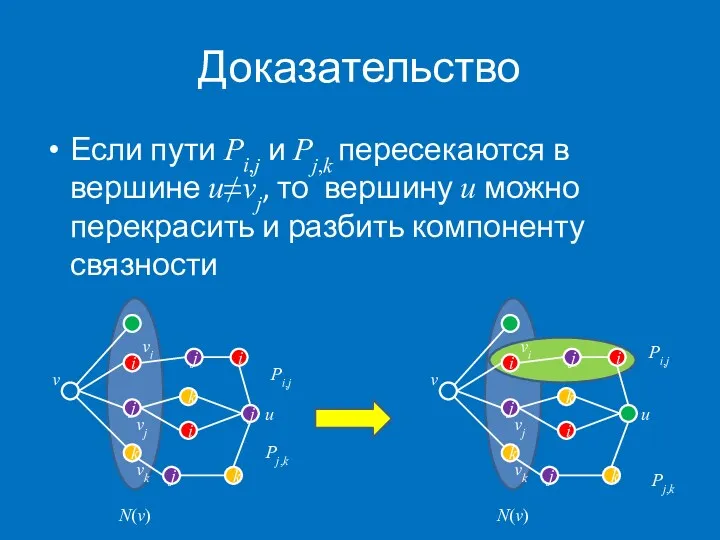
- 18. Доказательство Если пути Pi,j и Pj,k пересекаются в вершине u≠vj, то вершину u можно перекрасить и
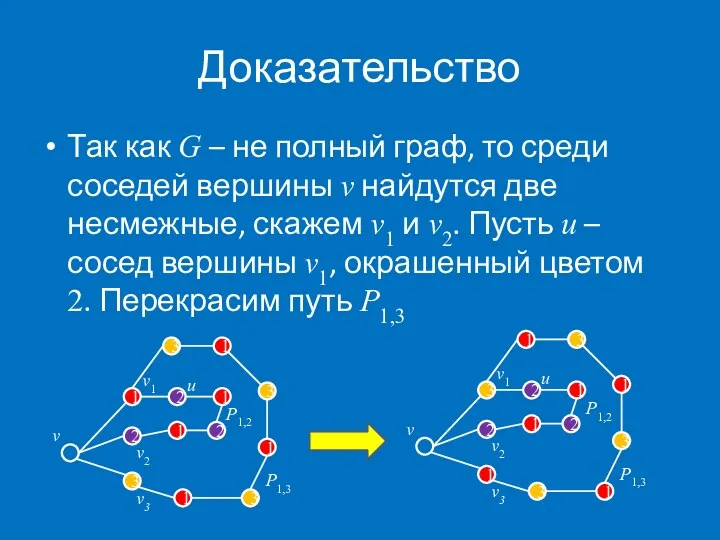
- 19. Доказательство Так как G – не полный граф, то среди соседей вершины v найдутся две несмежные,
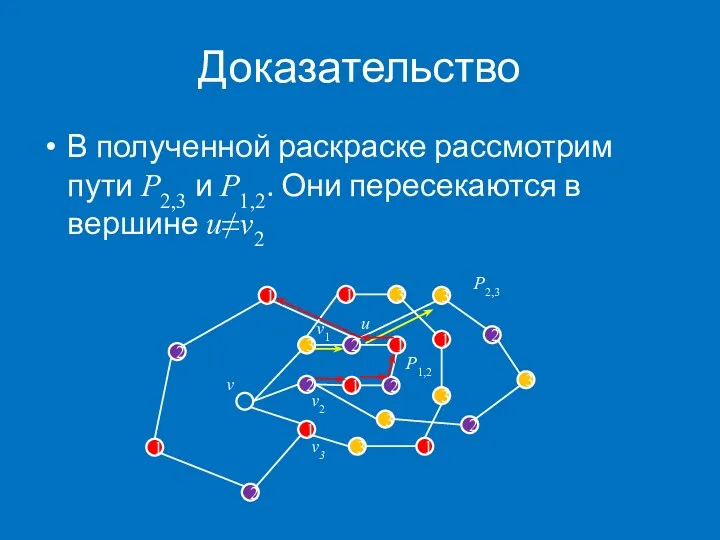
- 20. Доказательство В полученной раскраске рассмотрим пути P2,3 и P1,2. Они пересекаются в вершине u≠v2 1 2
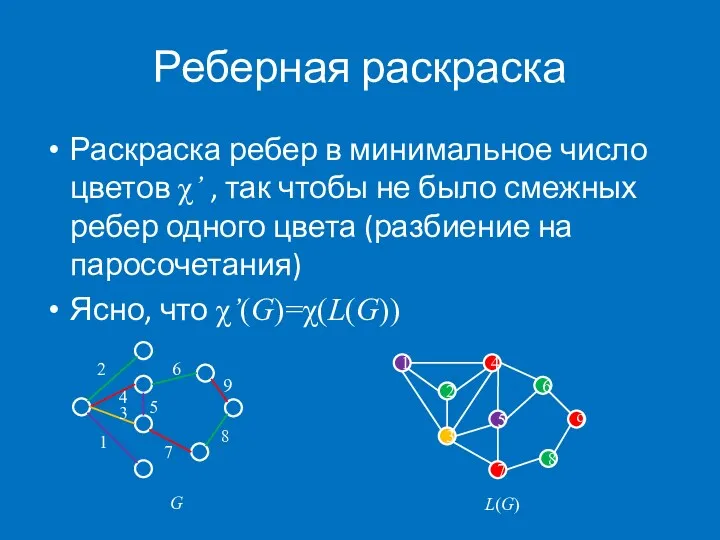
- 21. Реберная раскраска Раскраска ребер в минимальное число цветов χ’ , так чтобы не было смежных ребер
- 22. Очевидно, χ’(G)≥Δ Теорема Кёнига (1916). Если граф G двудольный, то χ’(G)=Δ Нижняя оценка
- 23. Доказательство Индукция по m Удалим ребро xy и раскрасим ребра оставшегося графа в Δ цветов по
- 24. Доказательство Пусть цвет a свободен при вершине x. Если он свободен и при вершине y, то
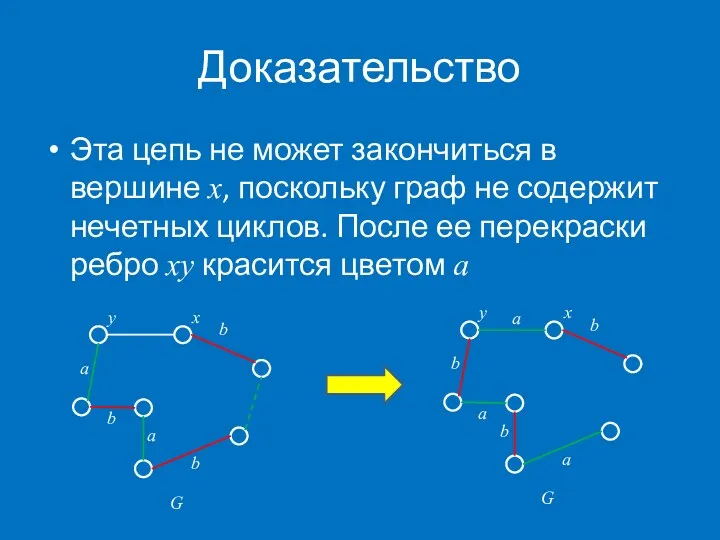
- 25. Доказательство Эта цепь не может закончиться в вершине x, поскольку граф не содержит нечетных циклов. После
- 26. Верхняя оценка Теорема Визинга (1964). Для любого графа G выполнена оценка χ’(G)≤Δ+1
- 27. Доказательство Индукция по m Для любого ребра xy, граф G\xy красится в Δ+1 цвет. Тогда при
- 28. Доказательство Удалим ребро xy0 и раскрасим полученный граф в Δ+1 цвет. Выберем при x и y0
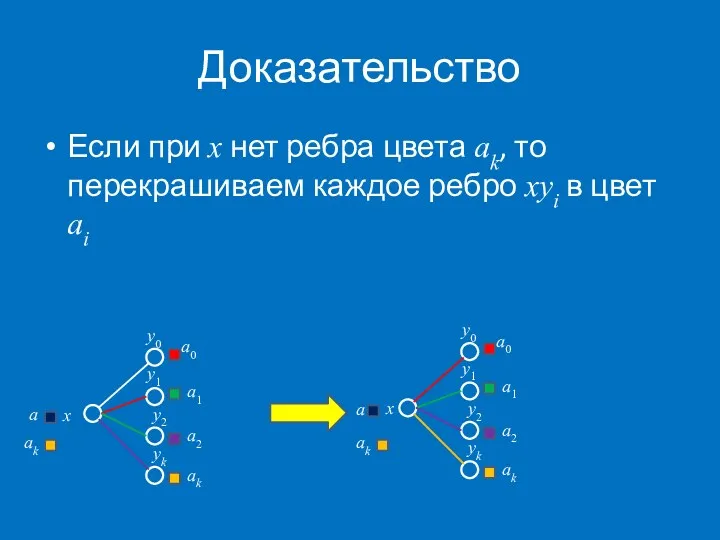
- 29. Доказательство Если при x нет ребра цвета ak, то перекрашиваем каждое ребро xyi в цвет ai
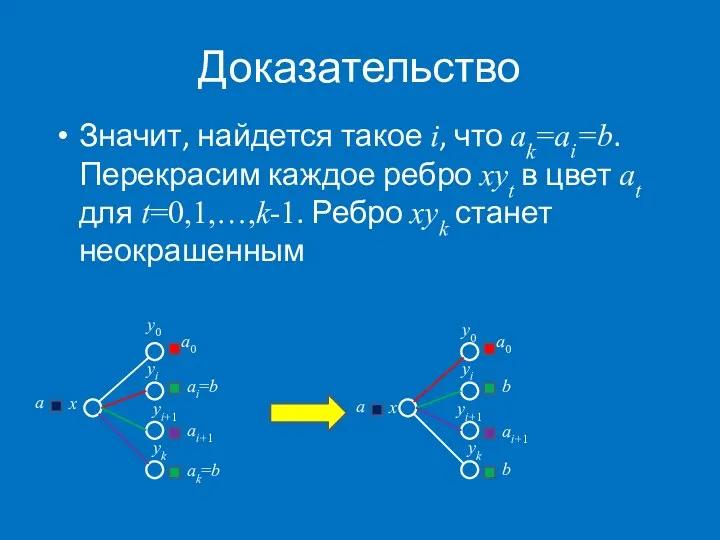
- 30. Доказательство Значит, найдется такое i, что ak=ai=b. Перекрасим каждое ребро xyt в цвет at для t=0,1,…,k-1.
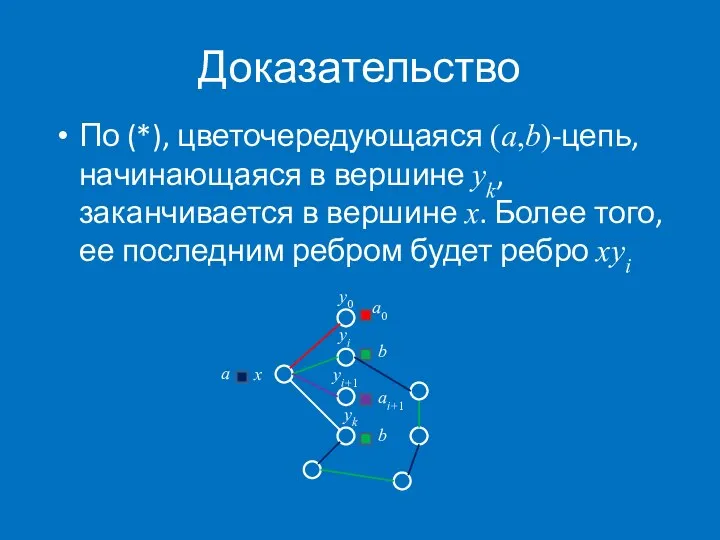
- 31. Доказательство По (*), цветочередующаяся (a,b)-цепь, начинающаяся в вершине yk, заканчивается в вершине x. Более того, ее
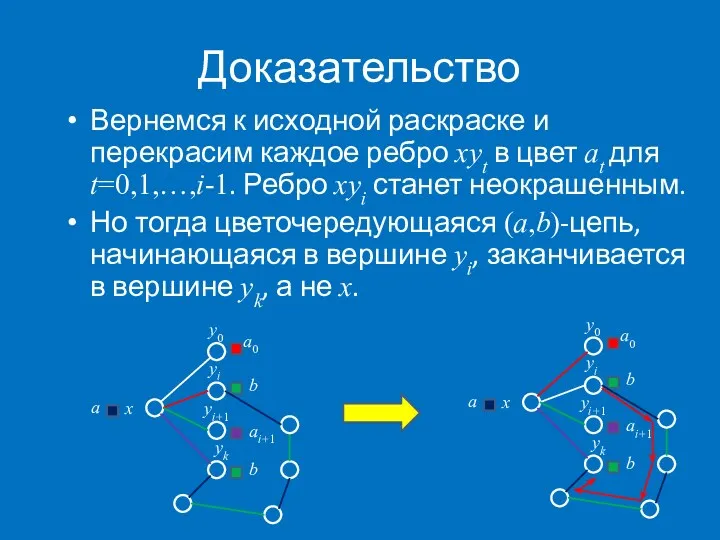
- 32. Доказательство Вернемся к исходной раскраске и перекрасим каждое ребро xyt в цвет at для t=0,1,…,i-1. Ребро
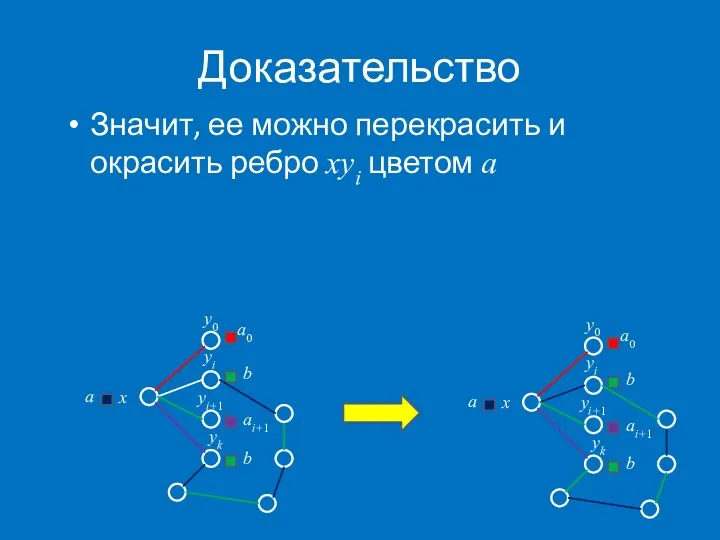
- 33. Доказательство Значит, ее можно перекрасить и окрасить ребро xyi цветом a x y0 yi a0 b
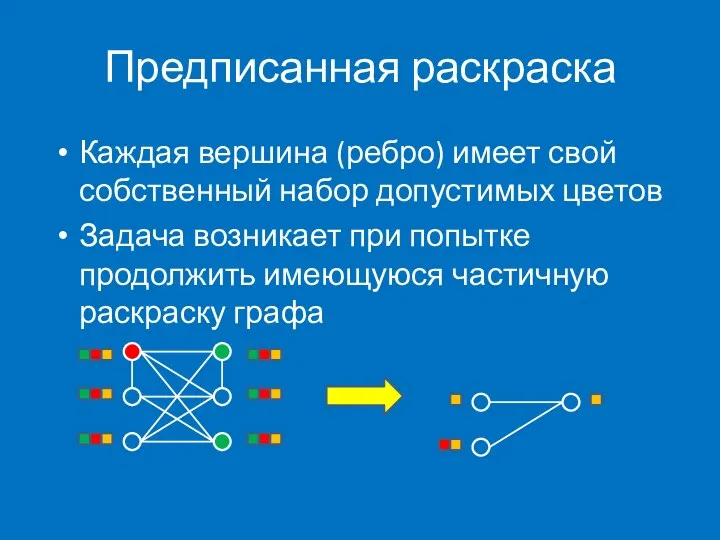
- 34. Предписанная раскраска Каждая вершина (ребро) имеет свой собственный набор допустимых цветов Задача возникает при попытке продолжить
- 35. Предписанное хроматическое число ch(G) Это минимальное k, при котором граф допускает правильную раскраску для любого предписания
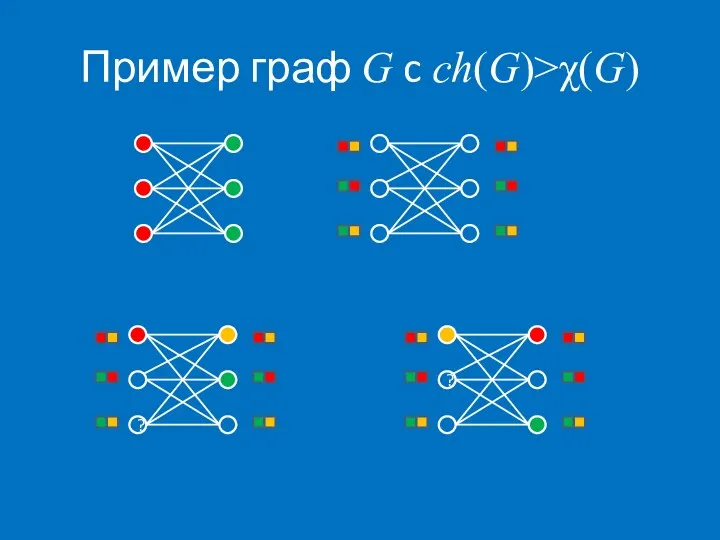
- 36. Пример граф G c ch(G)>χ(G) ? ?
- 37. Теорема. Для любого t≥3 существует двудольный граф G с ch(G)>t. Доказательство. G=Kt,tt Предписания меньшей доли: непересекающися
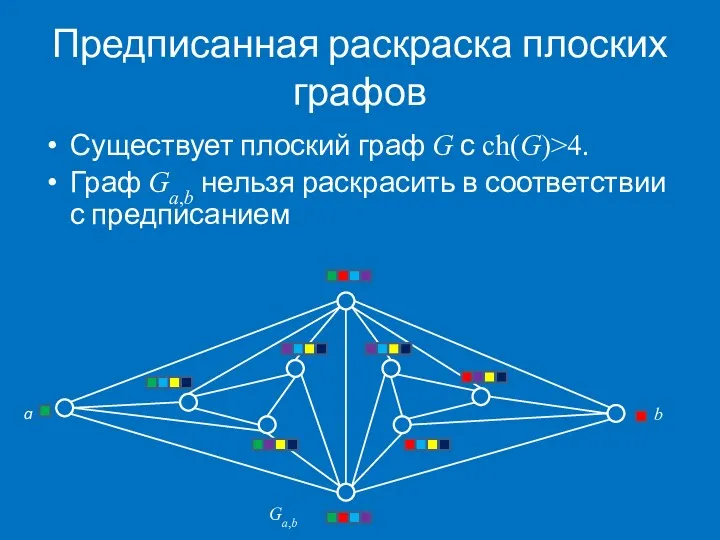
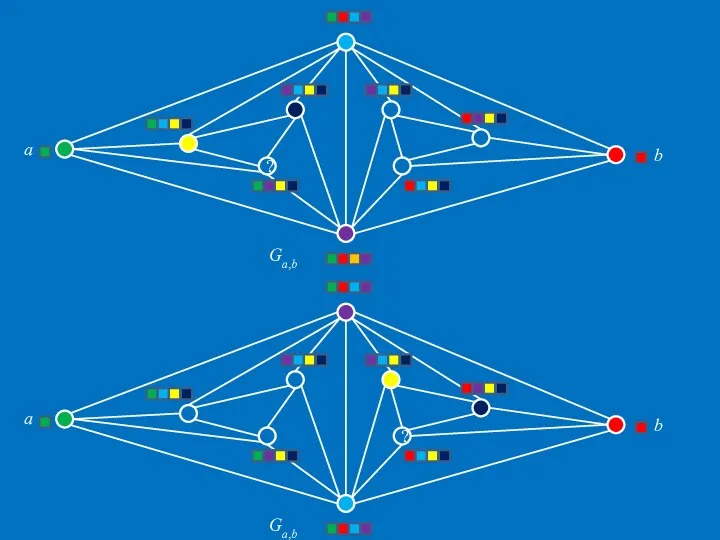
- 38. Предписанная раскраска плоских графов Существует плоский граф G с ch(G)>4. Граф Ga,b нельзя раскрасить в соответствии
- 39. ? b a Ga,b ? b Ga,b a
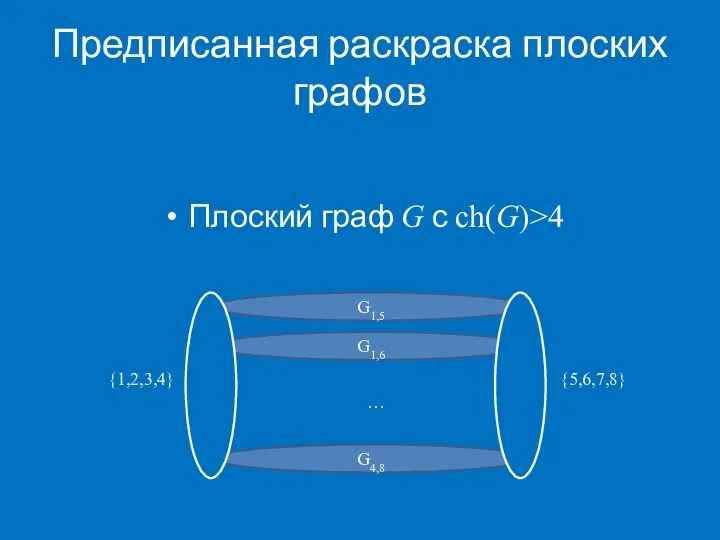
- 40. Предписанная раскраска плоских графов G1,5 G1,6 G4,8 {1,2,3,4} {5,6,7,8} … Плоский граф G с ch(G)>4
- 41. Предписанная раскраска плоских графов Теорема Томассена (1994). Если G – плоский, то ch(G)≤5
- 42. Предписанная раскраска плоских графов Лемма. Пусть в плоском графе G внешняя грань ограничена циклом C=v1v2…vk, а
- 43. Доказательство Индукция по n. Рассмотрим 2 случая Случай 1. В цикле C есть хорда xy. Обозначим
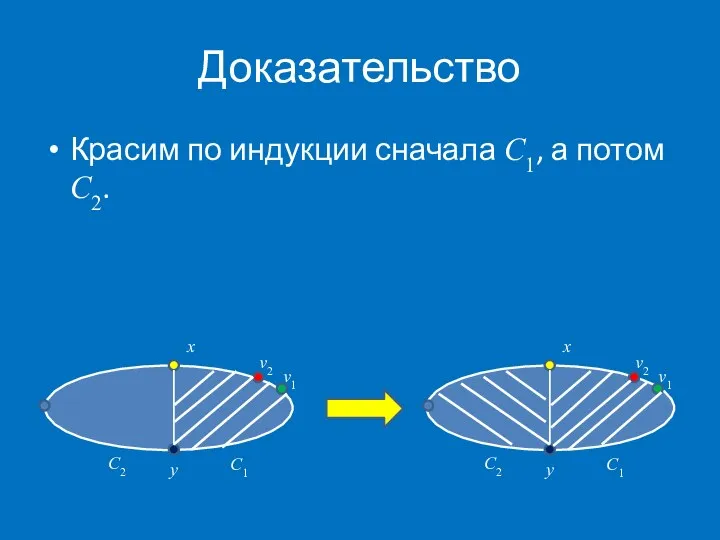
- 44. Доказательство x C2 v1 v2 y C1 x C2 v1 v2 y C1 Красим по индукции
- 45. Доказательство Случай 2. В цикле C нет хорд. Обозначим через u1,u2,…,us соседей вершины vk, лежащих внутри
- 46. Доказательство В предписании вершины vk выберем цвета c и d, отличные от a и удалим их
- 47. Доказательство По индукции раскрасим граф G’ в соответствии с предписанием. Цвета c и d не использовались
- 48. Предписанная раскраска ребер Гипотеза Визинга. Для любого графа G, ch’(G)=χ’(G). Теорема Галвина (1995). Если граф G
- 49. Лемма. Пусть в графе G задано вершинное предписание L. Предположим, ребра G можно ориентировать так, чтобы:
- 50. Доказательство леммы Индукция по n. Выберем цвет a и рассмотрим подграф G’, порожденный вершинами, чьи предписания
- 51. Доказательство теоремы Рассмотрим граф H=L(G). Построим для него ориентацию, удовлетворяющую условиям леммы. Пусть G=(X,Y; E). По
- 52. Доказательство теоремы Пусть e1 и e2 – два смежных в G ребра, причем f(e1)>f(e2). Тогда если
- 53. Доказательство теоремы Ясно, что |d+(v)|≤Δ−1, так как у дуги цвета k есть не более k−1 соседа
- 54. Доказательство теоремы Предположим, условие (2) леммы не выполнено. Рассмотрим минимальный по числу вершин подграф H’, который
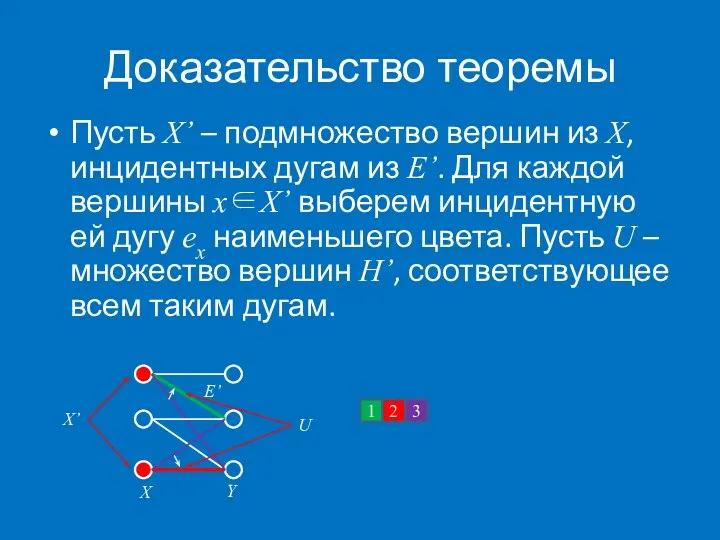
- 55. Доказательство теоремы Пусть X’ – подмножество вершин из X, инцидентных дугам из E’. Для каждой вершины
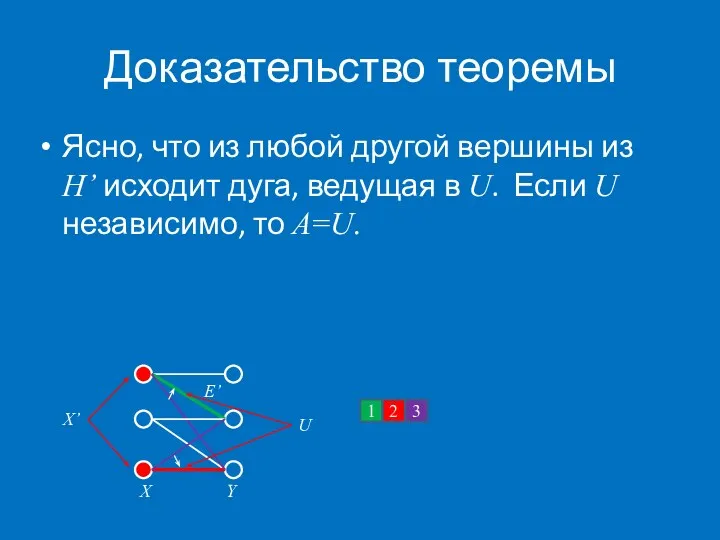
- 56. Доказательство теоремы Ясно, что из любой другой вершины из H’ исходит дуга, ведущая в U. Если
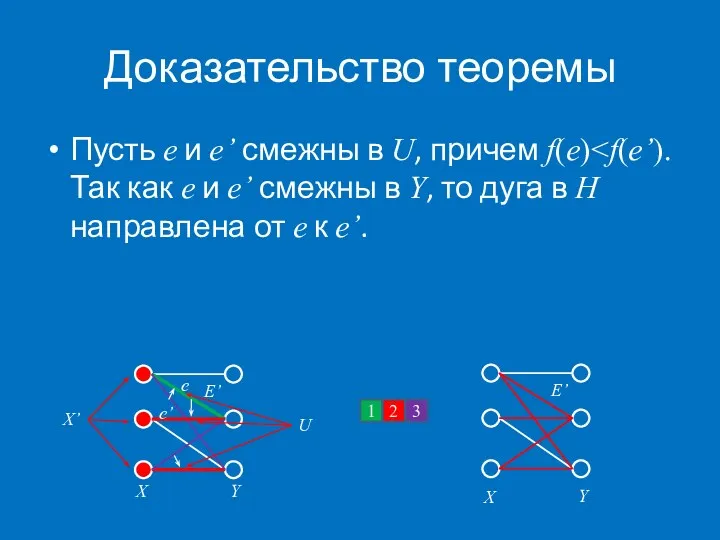
- 57. Доказательство теоремы Пусть e и e’ смежны в U, причем f(e) X E’ X’ 1 3
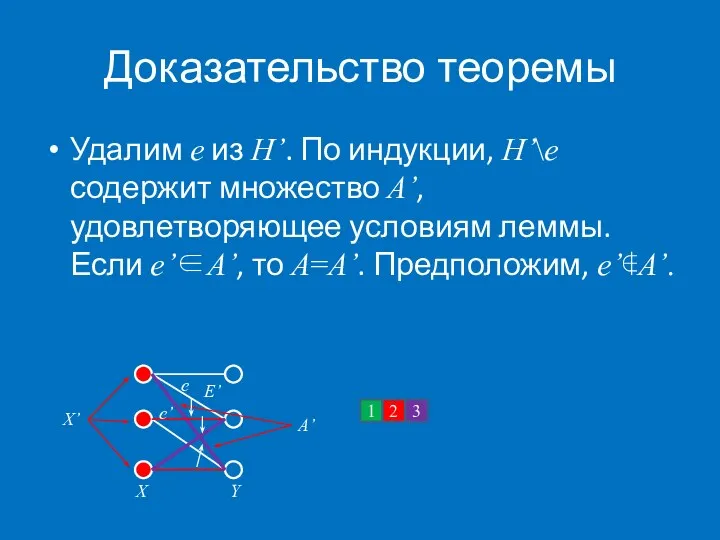
- 58. Доказательство теоремы Удалим e из H’. По индукции, H’\e содержит множество A’, удовлетворяющее условиям леммы. Если
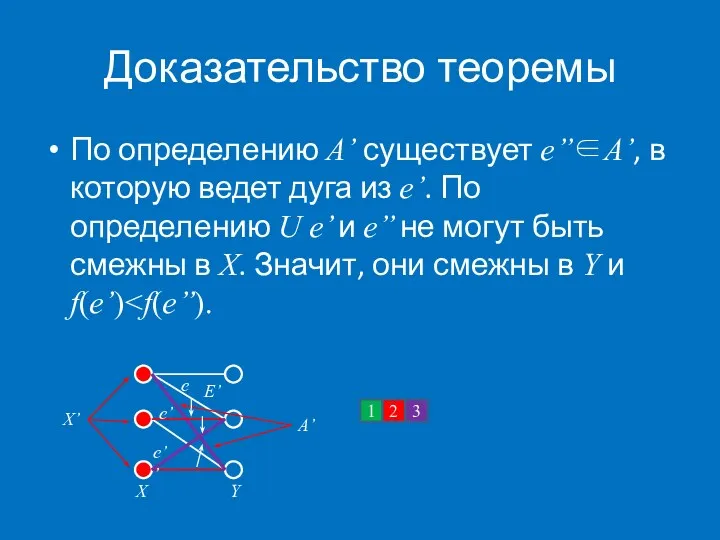
- 59. Доказательство теоремы По определению A’ существует e’’∈A’, в которую ведет дуга из e’. По определению U
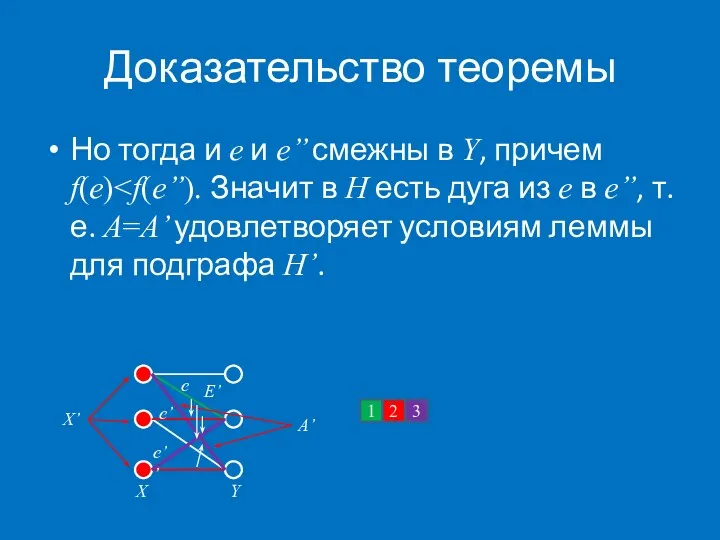
- 60. Доказательство теоремы Но тогда и e и e’’ смежны в Y, причем f(e) X E’ X’
- 61. Упражнения 1. Доказать, что если G’ – это дополнение G, то max{χ(G),χ(G’)}≥n1/2 2. Доказать, что χ(G)≤
- 63. Скачать презентацию





























 Презентация к уроку в 1 классе по теме Килограмм по программе Школа России.
Презентация к уроку в 1 классе по теме Килограмм по программе Школа России. Сложение и вычитание десятичных дробей. Урок математики в 5 классе
Сложение и вычитание десятичных дробей. Урок математики в 5 классе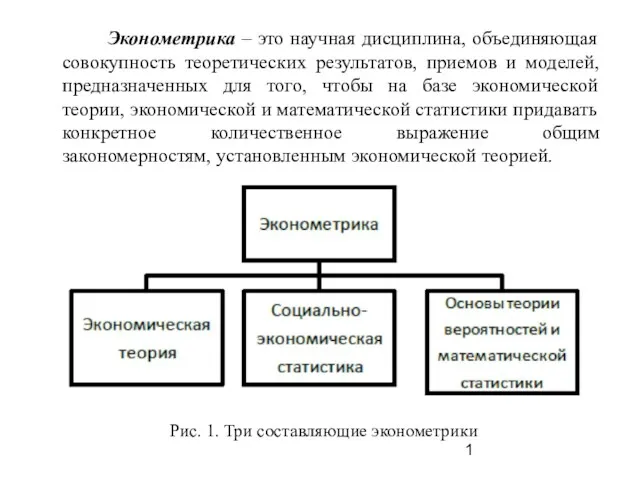 Эконометрика. Три составляющие эконометрики
Эконометрика. Три составляющие эконометрики История возникновения чисел. Главное число человека
История возникновения чисел. Главное число человека Сравнение дробей
Сравнение дробей Различные способы умножения. Проектная работа
Различные способы умножения. Проектная работа Магический квадрат
Магический квадрат Число и цифра 5. Состав Числа 5.
Число и цифра 5. Состав Числа 5. Нитяная геометрия. Внеурочная образовательная занятость обучающихся при изучении математики в 5-6 классах
Нитяная геометрия. Внеурочная образовательная занятость обучающихся при изучении математики в 5-6 классах Методы решения систем уравнений. Метод подстановки
Методы решения систем уравнений. Метод подстановки Обчислення виду 18 – 5. Складання за малюнком задачі на знаходження суми та задачі на різницеве порівняння. Урок №82
Обчислення виду 18 – 5. Складання за малюнком задачі на знаходження суми та задачі на різницеве порівняння. Урок №82 Методы преобразования чертежа. (Лекция 9)
Методы преобразования чертежа. (Лекция 9) Вычитание смешанных чисел с переходом через единицу
Вычитание смешанных чисел с переходом через единицу Сложение чисел с разными знаками. Алгоритм выполнения сложения
Сложение чисел с разными знаками. Алгоритм выполнения сложения Метод экспертных оценок
Метод экспертных оценок Математический диктант. Прямоугольник, ромб, квадрат. Геометрия, 8 класс
Математический диктант. Прямоугольник, ромб, квадрат. Геометрия, 8 класс Среднее арифметическое
Среднее арифметическое Степень числа. Тайны степени
Степень числа. Тайны степени ЕГЭ по математике - 2012. Решаем B13
ЕГЭ по математике - 2012. Решаем B13 Роль математической статистики в медицине и здравоохранении
Роль математической статистики в медицине и здравоохранении Презентация к уроку по математике (старшая группа) по теме: Методический театр- сказка.
Презентация к уроку по математике (старшая группа) по теме: Методический театр- сказка.  Логарифм. Основные свойства логарифмов
Логарифм. Основные свойства логарифмов Таблица умножения и деления на 2. Игра-тренажер
Таблица умножения и деления на 2. Игра-тренажер Число и цифра 9
Число и цифра 9 Длина окружности. Число π. 6 класс
Длина окружности. Число π. 6 класс 1 детская научно-практическая конференция по теме Линия жизни.
1 детская научно-практическая конференция по теме Линия жизни. урок_23
урок_23 Математика в повседневной жизни
Математика в повседневной жизни