Содержание
- 2. 1. ОБЩИЕ ПОЛОЖЕНИЯ Случайное явление — это такое явление, которое при неоднократном воспроизведении одного и того
- 3. Несовместимыми называют два события, если появление одного из них исключает возможность появления другого. Например, отказ и
- 4. Независимыми считают такие события, появление которых не зависит от того, какое событие произошло перед этим (например,
- 5. В качестве единицы измерения вероятности принимают вероятность достоверного события, т. е. такого события, которое в результате
- 6. Случайная величина — это величина, которая в результате опыта может принимать различные значения, причем заранее неизвестно
- 7. Вероятность события изменяется от 0 до 1 или в общем случае определяется по формуле 1: P(a)
- 8. Для независимых событий вероятность произведения равна произведению их вероятностей (теорема умножения) (2)
- 11. 2. Характеристики случайных величин Среднее арифметическое значение — это частное от деления суммы полученных из опытов
- 12. Математическое ожидание — сумма произведений всех возможных значений случайной величины на вероятности этих значений. Между средним
- 13. Мода случайной величины — наиболее вероятное ее значение, т. е. значение, которому соответствует наибольшая частота. Графически
- 15. Размах рассеивания случайной величины — это разность между максимальным и минимальным ее значениями, полученными в результате
- 16. Среднее квадратичное отклонение также является мерой рассеивания и равно корню квадратному из дисперсии. Поскольку среднее квадратичное
- 17. Среднее квадратичное отклонение, выраженное в долях среднего арифметического, носит название коэффициента вариации. или Введение коэффициента вариации
- 18. 3. Основные понятия экспоненциального закона распределения Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными
- 19. Дифференциальная функция экспоненциального закона: λ — параметр распределения (постоянный коэффициент). У экспоненциального распределения математическое ожидание и
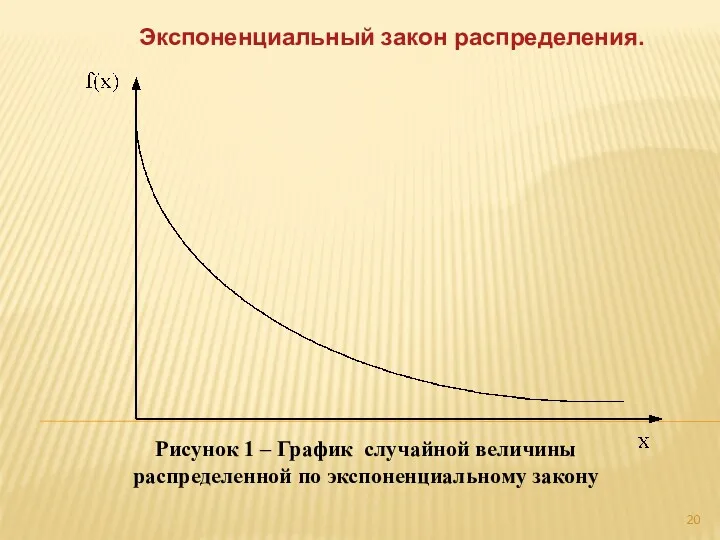
- 20. Экспоненциальный закон распределения. Рисунок 1 – График случайной величины распределенной по экспоненциальному закону
- 21. Графическая интерпретация экспоненциального распределения представлена на рисунке 1. При исследовании надежности автомобиля характеризует интенсивность отказа невосстанавливаемых
- 22. 2. Принципы применения нормального закона распределения Нормальный закон распределения встречается достаточно часто. Плотность распределения его находят
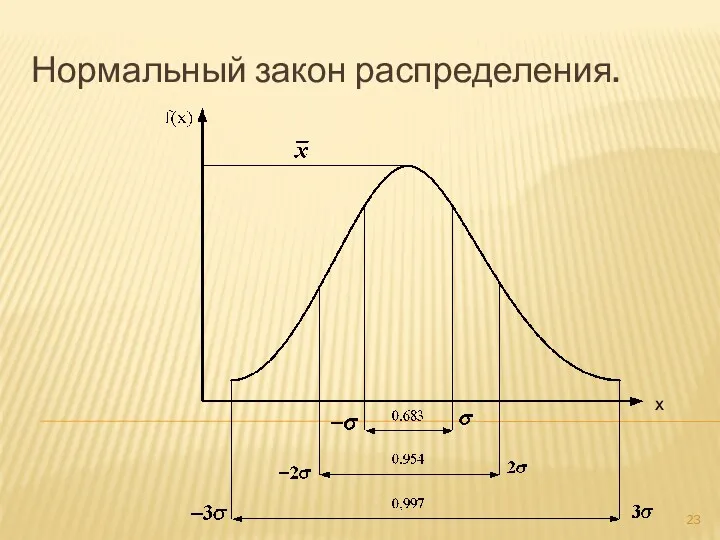
- 23. Нормальный закон распределения. х
- 24. Величина Х (среднее арифметическое) показывает смещение кривой f(х) вдоль оси абсцисс без изменения ее формы, т.
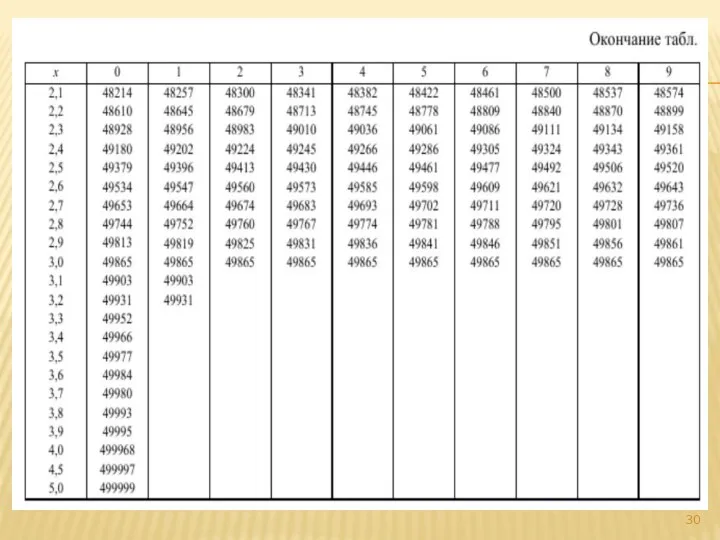
- 25. Если в качестве аргумента в формуле принять безразмерную переменную: получим стандартный закон нормального распределения: Нормальный закон
- 26. Нормальное распределение применяется для описания отказов, вызванных изнашиванием или постепенным накоплением неисправностей, когда доля внезапных отказов
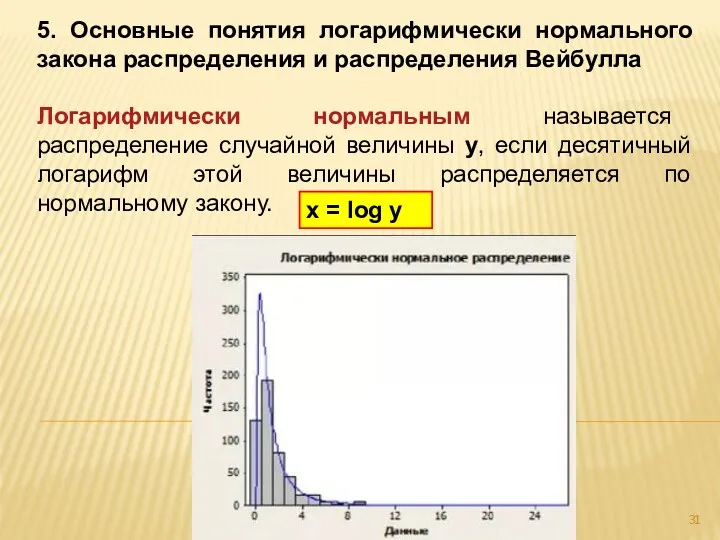
- 31. 5. Основные понятия логарифмически нормального закона распределения и распределения Вейбулла Логарифмически нормальным называется распределение случайной величины
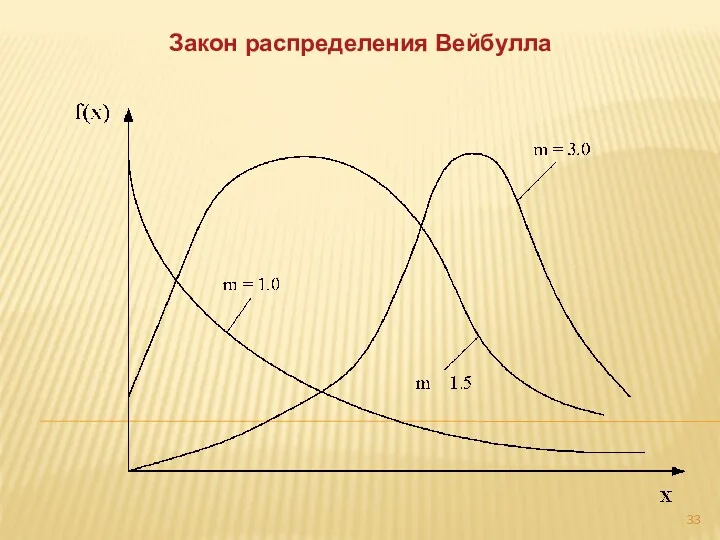
- 32. Закон распределения Вейбулла описывается дифференциальной функцией: m, a — параметры распределения. Значение параметра m зависит от
- 33. Закон распределения Вейбулла
- 34. При m=1 распределение Вейбулла преобразуется в экспоненциальное. При m = 2,5...3,5 и V = 0,3...0,4 —
- 35. Это наиболее распространенный закон распределения при обработке экспериментальных данных по надежности автомобилей в эксплуатации; теоретически начинается
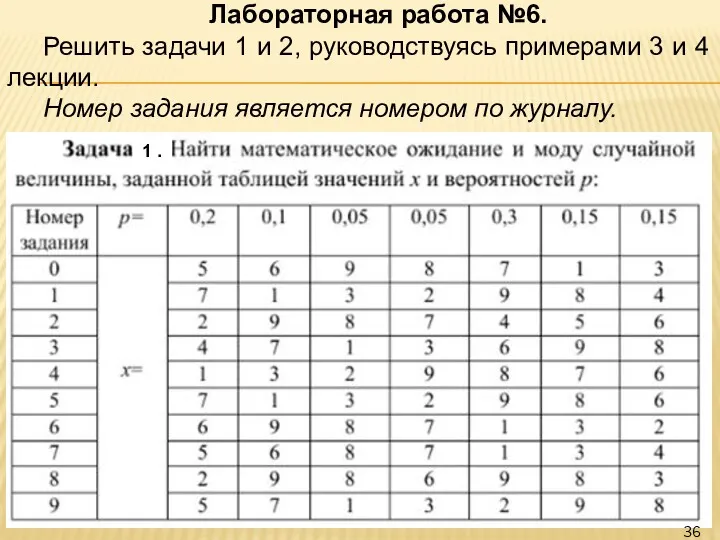
- 36. 1 . Лабораторная работа №6. Решить задачи 1 и 2, руководствуясь примерами 3 и 4 лекции.
- 38. Скачать презентацию





























 Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Конспект урока по математике в 1 классе УМК Гармония
Конспект урока по математике в 1 классе УМК Гармония Перспективная модель ОГЭ-2020 по математике
Перспективная модель ОГЭ-2020 по математике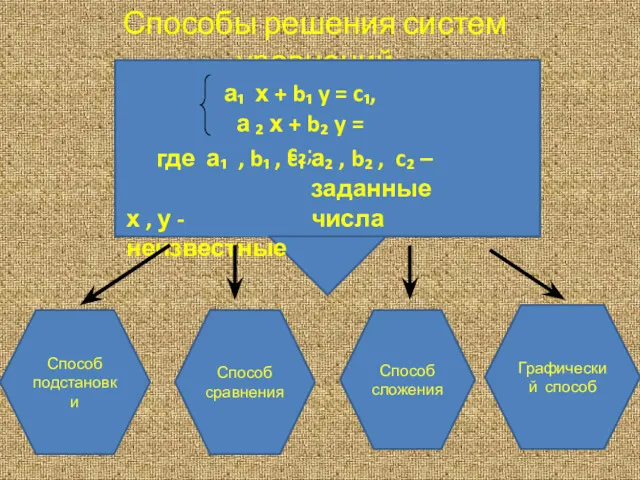 Способы решения систем уравнений (3)
Способы решения систем уравнений (3) Умножение числа 2 и на 2
Умножение числа 2 и на 2 Какова масса самой маленькой птицы наших лесов?
Какова масса самой маленькой птицы наших лесов? Умножение десятичных дробей. Математика. 5 класс
Умножение десятичных дробей. Математика. 5 класс Понятие функции, способы её задания, график функции. Преобразование графиков
Понятие функции, способы её задания, график функции. Преобразование графиков Алгоритмы Брезенхема
Алгоритмы Брезенхема Показательная функция, её свойства и график
Показательная функция, её свойства и график Устный счет
Устный счет Деление отрицательных чисел и чисел с разными знаками
Деление отрицательных чисел и чисел с разными знаками Графический метод решения системы уравнений с двумя переменными. 7 класс
Графический метод решения системы уравнений с двумя переменными. 7 класс Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Делим поровну
Делим поровну Розв'язуємо задачі на різницеве порівняння двох добутків. Урок №81
Розв'язуємо задачі на різницеве порівняння двох добутків. Урок №81 Вписанная окружность
Вписанная окружность Прямая и обратная пропорциональные зависимости. 6 класс
Прямая и обратная пропорциональные зависимости. 6 класс Проценты. 5 класс
Проценты. 5 класс Найди отличия
Найди отличия Қарапайым математикалық түсініктер. Уақытты бағдарлау
Қарапайым математикалық түсініктер. Уақытты бағдарлау методическая разработка по развитию логического мышления у старших дошкольников с использованием блоков Дьенеша
методическая разработка по развитию логического мышления у старших дошкольников с использованием блоков Дьенеша Математика повсюду
Математика повсюду Смежные и вертикальные углы
Смежные и вертикальные углы Решение дробных рациональных уравнений
Решение дробных рациональных уравнений Решение квадратных уравнений
Решение квадратных уравнений презентация по математике Число и цифра 4
презентация по математике Число и цифра 4 Решение уравнений. Урок математики
Решение уравнений. Урок математики