Содержание
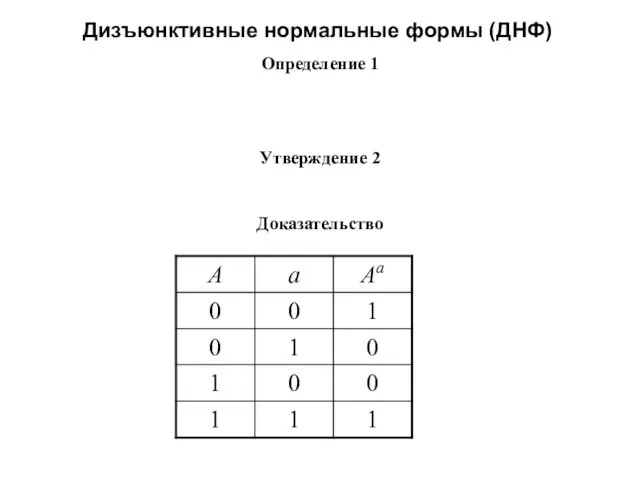
- 2. Дизъюнктивные нормальные формы (ДНФ) Определение 1 Утверждение 2 Доказательство
- 3. Определение 3 Общий вид элементарной конъюнкции: Конъюнкция логических переменных или их отрицаний называется элементарной конъюнкцией (ЭК).
- 4. Примеры
- 5. Теорема Любое высказывание приводимо к ДНФ. Схема приведения высказывания к ДНФ Избавиться от импликации и эквивалентности,
- 6. Пример Привести высказывание к ДНФ
- 7. Построение высказываний по таблице истинности. Совершенные дизъюнктивные нормальные формы (СДНФ) Определение 1 Пусть – некоторое множество
- 8. Определение 2 Дизъюнктивная нормальная форма называется совершенной (СДНФ), если все составляющие ее элементарные конъюнкции являются полными.
- 9. Приведение высказывания к СДНФ Теорема Высказывание, не являющееся тождественно ложным, приводимо к СДНФ. Правило приведения высказывания
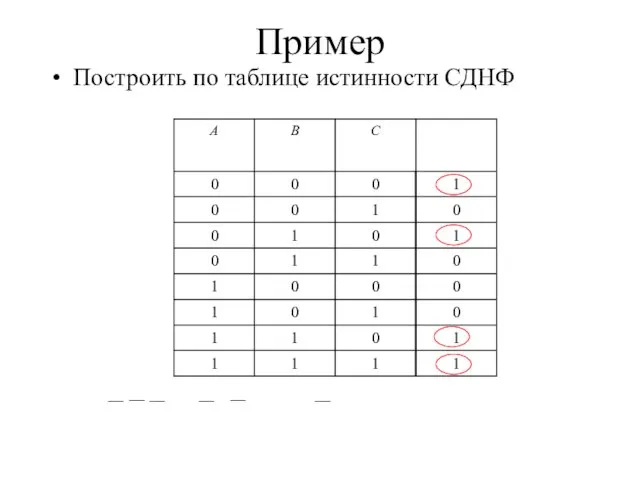
- 10. Пример Построить по таблице истинности СДНФ
- 11. Задача «Вернувшись домой, Мегрэ позвонил на набережную Орфевр. - Говорит Мегрэ. Есть новости? - Да, шеф.
- 12. Решение задачи Пусть P=« Франсуа был пьян» L=«Франсуа лжет» I=«Этьен убийца» U=«Убийство произошло после полуночи» Тогда
- 13. Приложения алгебры высказываний. Исследование переключательных схем Переключательная схема — это схематическое изображение некоторого устройства, состоящего из
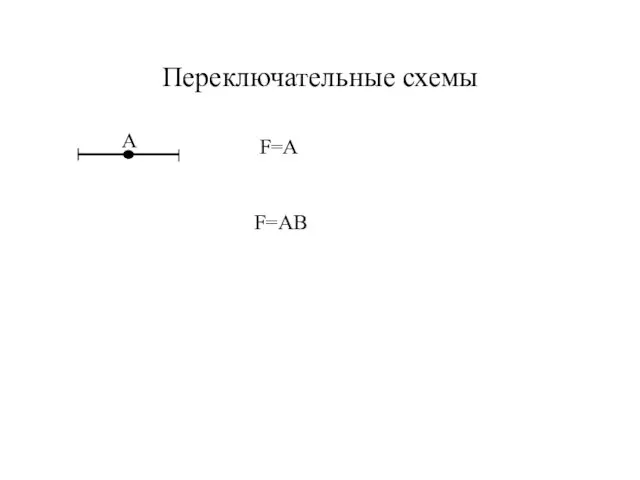
- 14. Переключательные схемы A F=A F=AB
- 15. Переключательные схемы Пример 1
- 16. Переключательные схемы. Пример 1
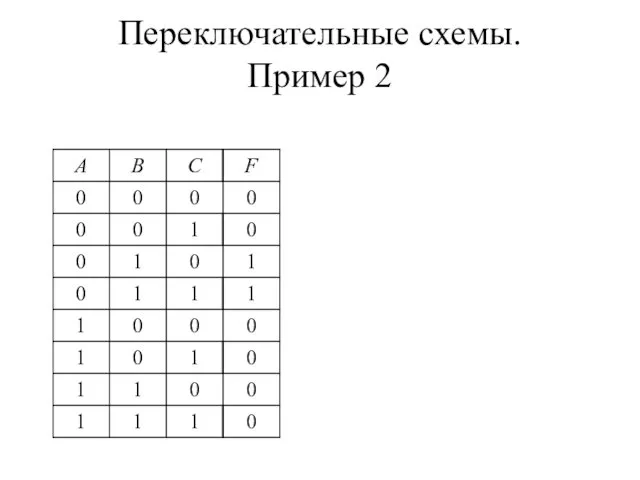
- 17. Переключательные схемы. Пример 2
- 18. Переключательные схемы. Пример 2
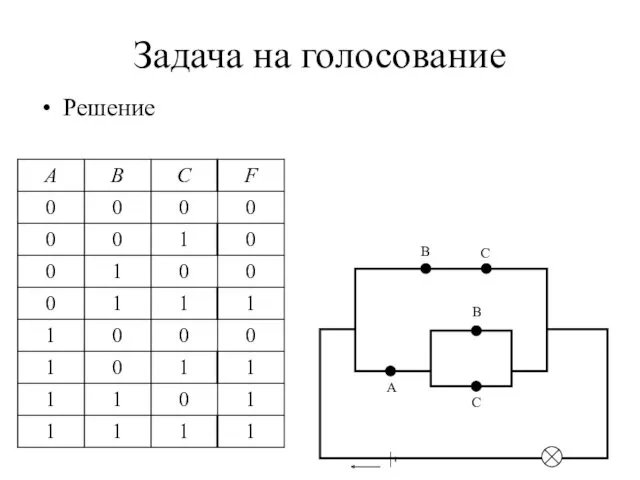
- 19. Задача на голосование Построить контактную схему для оценки результатов спортивного соревнования тремя судьями при условиях: судья
- 20. Задача на голосование Решение
- 21. Задачи 2. Голосуют три человека A, B, C. Предложение принимается большинством голосов, причём C - председатель,
- 23. Скачать презентацию















 Почему мы до сих пор пользуемся клавиатурой
Почему мы до сих пор пользуемся клавиатурой Шумовой оркестр как средство формирования музыкальных способностей детей дошкольного возраста
Шумовой оркестр как средство формирования музыкальных способностей детей дошкольного возраста Ребусы
Ребусы Перспективный план по безопасному поведению детей старшего возраста в детском саду
Перспективный план по безопасному поведению детей старшего возраста в детском саду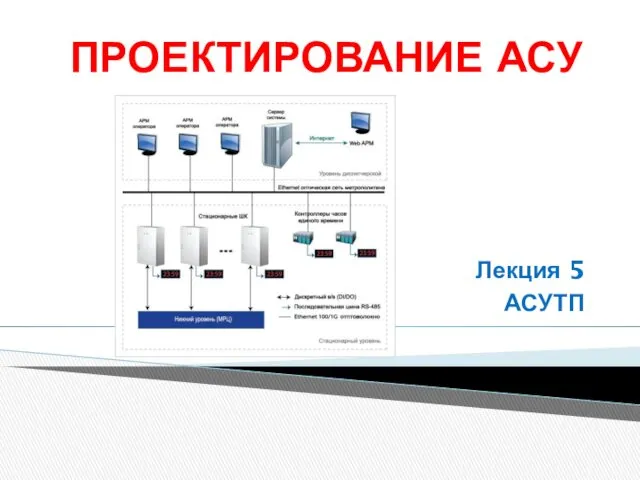 Проектирование АСУ. Определение АСУТП
Проектирование АСУ. Определение АСУТП Консультация для родителей Глаза зеркало души
Консультация для родителей Глаза зеркало души Семейный бюджет. Что такое семейный бюджет
Семейный бюджет. Что такое семейный бюджет Present Simple Tense
Present Simple Tense Prezentatsia_Ermak_URALCHEM1
Prezentatsia_Ermak_URALCHEM1 Презентация к уроку русского языка по теме Омонимы
Презентация к уроку русского языка по теме Омонимы ПОСТРОЕНИЕ РАЗВИВАЮЩЕЙ СРЕДЫ ПО ФГОС
ПОСТРОЕНИЕ РАЗВИВАЮЩЕЙ СРЕДЫ ПО ФГОС Номинация Методические материалы для использования в ООШ, СОШ, УДОД 4 -7 классы Этих дней не смолкнет слава
Номинация Методические материалы для использования в ООШ, СОШ, УДОД 4 -7 классы Этих дней не смолкнет слава The simpsons. Parts of the body
The simpsons. Parts of the body Блюда из мяса
Блюда из мяса Структура современного урока
Структура современного урока Ценностное предложение
Ценностное предложение Презентация Центр познавательно-исследовательской деятельности
Презентация Центр познавательно-исследовательской деятельности Презентация Первоцветы в нашем детском
Презентация Первоцветы в нашем детском Александр Иванович Куприн. Повесть Гранатовый браслет. Смысл спора о бескорыстной любви
Александр Иванович Куприн. Повесть Гранатовый браслет. Смысл спора о бескорыстной любви Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника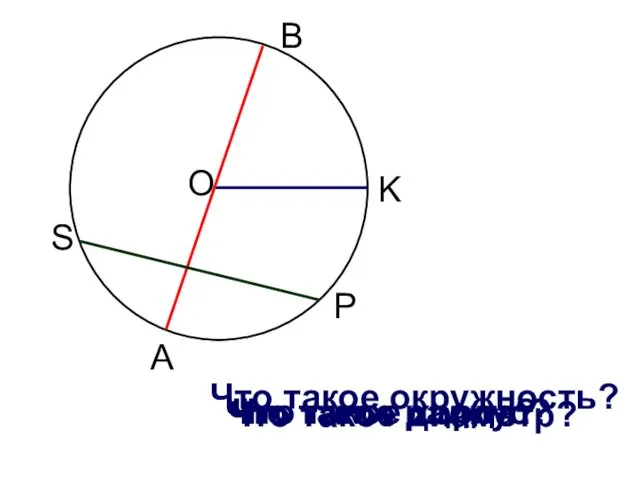 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности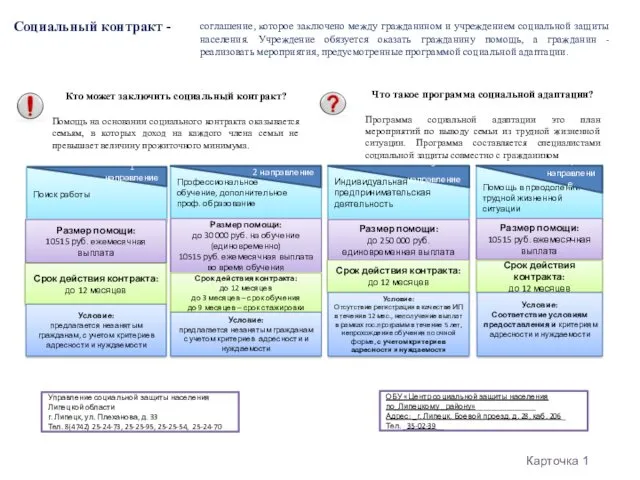 Социальный контракт
Социальный контракт Дивертикулярная болезнь
Дивертикулярная болезнь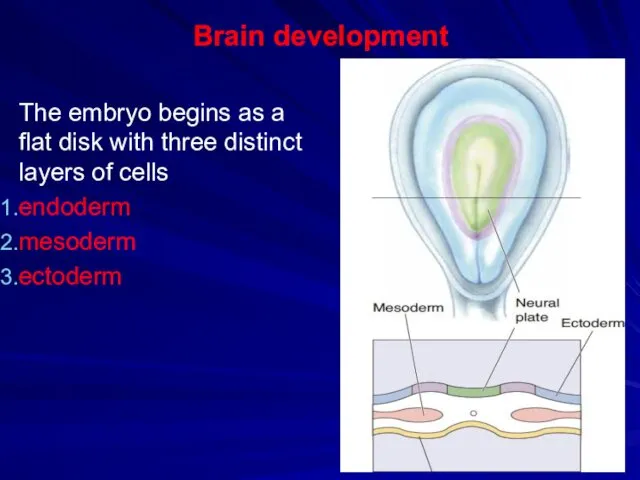 Brain development
Brain development Математические методы в теории надежности
Математические методы в теории надежности Основные сведения о сварке (Тема 6)
Основные сведения о сварке (Тема 6) План и карта
План и карта Перелетные птицы. Для детей старшего дошкольного возраста,
Перелетные птицы. Для детей старшего дошкольного возраста,