Содержание
- 2. Цель лекции – изучить комбинаторные конфигурации «сочетания» и «размещения», свойства и формулы подсчета их количества
- 3. Литература Глускин Л.М., Шор Л.А., Шварц В.Я. Задачи и алгоритмы комбинаторики, и теории графов. Донецк, ДПИ,
- 4. Базовые понятия: Множество Бином Биномиальные коэффициенты и формула для них Перестановка Термины Ключевые слова: Сочетание Размещение
- 5. Сочетания Def: произвольное k-элементное подмножество n-элементного множества называется сочетанием из n элементов по k. В сочетаниях
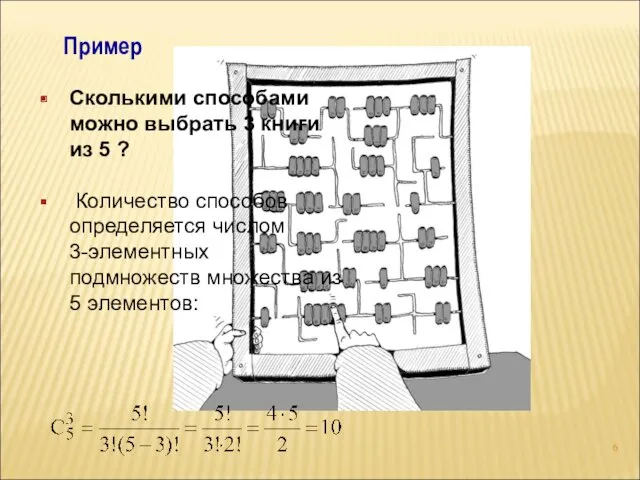
- 6. Пример Сколькими способами можно выбрать 3 книги из 5 ? Количество способов определяется числом 3-элементных подмножеств
- 7. Геометрическая интерпретация чисел Рассмотрим прямоугольную сетку квадратов размерами (“шахматный город“ – Манхеттен) Он состоит из прямоугольных
- 8. Любой кратчайший путь из точки (0; 0) в точку (m; n) состоит из m+n отрезков, из
- 9. Количество подмножеств данного множества – мощность булеана Сколько всего подмножеств имеет множество М, состоящее из n
- 10. TIME-OUT
- 11. Размещения. (Упорядоченные подмножества данного множества) Дано неупорядоченное множество М, состоящее из n элементов: | M |
- 12. Размещения. Определение Def: упорядоченные k-элементные подмножества множества из n элементов называются размещениями из n элементов по
- 13. Количество размещений. Связь с перестановками Теорема Число упорядоченных k-элементных подмножеств множества М, состоящего из n элементов,
- 14. Пример В турнире участвуют 8 команд. Сколько различных предсказаний (прогнозов) относительно первых трех первых мест по
- 15. Размещения с повторениями и их количество Def: любой упорядоченный набор k элементов с повторениями из элементов
- 16. Сочетания с повторениями и их количество Объединим все размещения с повторением из n элементов по k,
- 17. ВЫВОДЫ: СВЯЗЬ РАЗМЕЩЕНИЙ И СОЧЕТАНИЙ Два размещения с повторениями или без принадлежат одному сочетанию с повторениями
- 19. Скачать презентацию














 Мастер-класс Структура логопедического занятия
Мастер-класс Структура логопедического занятия Портфоліо учителя математики Кашенець Тетяни Миколаївни
Портфоліо учителя математики Кашенець Тетяни Миколаївни Introduction to information security
Introduction to information security Жития новомучеников и исповедников Церкви Русской Истринской земли
Жития новомучеников и исповедников Церкви Русской Истринской земли موضوع عن االهداف التعليمية
موضوع عن االهداف التعليمية Академия гражданской защиты МЧС России
Академия гражданской защиты МЧС России презентация Развитие творческих способностей детей раннего возраста в продуктивной (конструктивной) деятельности.
презентация Развитие творческих способностей детей раннего возраста в продуктивной (конструктивной) деятельности. С днем учителя, дорогие и любимые преподаватели
С днем учителя, дорогие и любимые преподаватели Права и свободы человека и гражданина РФ
Права и свободы человека и гражданина РФ Хозяйство Европейского Юга
Хозяйство Европейского Юга Радиоприемные устройства РЛС. Устройства адаптации
Радиоприемные устройства РЛС. Устройства адаптации 2012 год - год истории
2012 год - год истории Состояние мирового уровня энергоменеджмента, международные инструменты стимулирования энергосбережения
Состояние мирового уровня энергоменеджмента, международные инструменты стимулирования энергосбережения Педагогический опыт (презентация)
Педагогический опыт (презентация) 20230923_prilozhenie_2
20230923_prilozhenie_2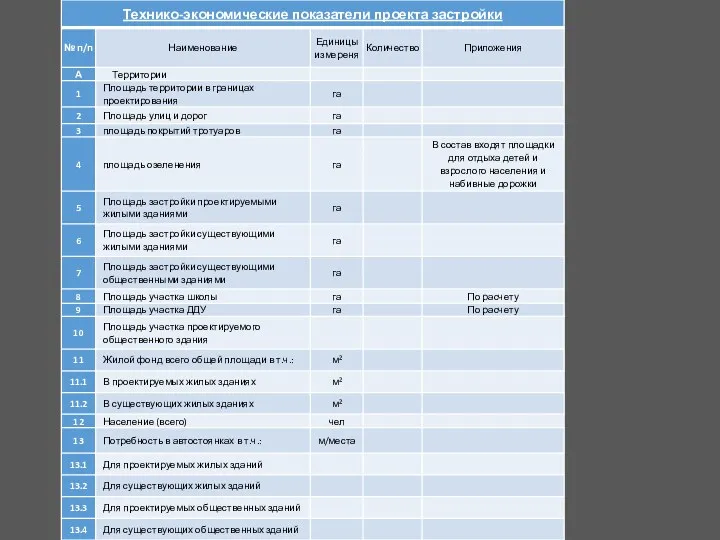 Технико-экономические показатели проекта застройки
Технико-экономические показатели проекта застройки Шизофрения. Основные гипотезы патогенеза. Клинические формы и типы течения. Общие принципы лечения
Шизофрения. Основные гипотезы патогенеза. Клинические формы и типы течения. Общие принципы лечения Загальні поняття про радіоперешкоди. Огляд методів захисту від перешкод. (Тема 6.1)
Загальні поняття про радіоперешкоди. Огляд методів захисту від перешкод. (Тема 6.1) Радіометричні поліпшуючі перетворення. Лабораторна робота №19
Радіометричні поліпшуючі перетворення. Лабораторна робота №19 клас укр яз
клас укр яз Основні засади стандартизації: мета, задачі, принципи
Основні засади стандартизації: мета, задачі, принципи Триггеры в презентации
Триггеры в презентации Концепція об’єктно-орієнтованого програмування: базові поняття та основні принципи
Концепція об’єктно-орієнтованого програмування: базові поняття та основні принципи Жанры изобразительного искусства
Жанры изобразительного искусства Церковь Христова
Церковь Христова Линейные электрические цепи постоянного тока
Линейные электрические цепи постоянного тока Презентация Времена года
Презентация Времена года Факторы и условия, повышающие эффективность тренировочной и соревновательной деятельности
Факторы и условия, повышающие эффективность тренировочной и соревновательной деятельности