Dividing polynomials презентация

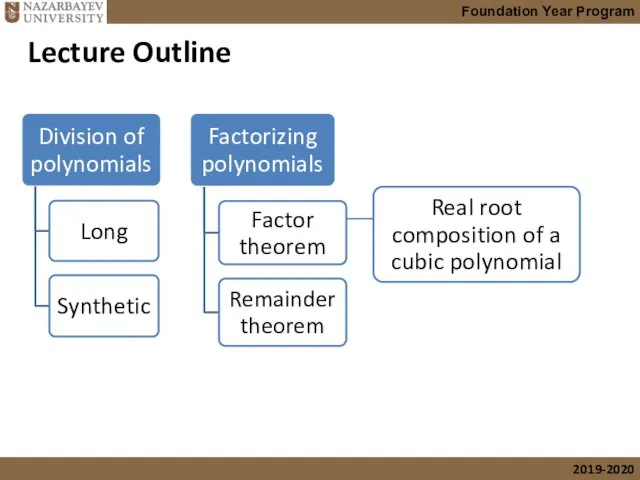
Lecture Outline

Introduction

1.4.1 Divide a polynomial by another polynomial using long division
Dividing polynomials is much like the familiar process of dividing numbers. When we divide 38 by 7, the quotient is 5 and the remainder is 3.
We write 38 = 7 x 5 + 3
or, alternatively,

1.4.1 Divide a polynomial by another polynomial using long division
! The word ‘remainder’ is pronounced as [rɪˈmeɪn.dər]

cont’d

We repeat the process using the last line –2x + 12 as the dividend.
4

The division process ends when the last line is of lesser degree than the divisor. The last line then contains the remainder, and the top line contains the quotient.
The result of the division can be interpreted in either of two ways:
or
cont’d

Solution

1.4.2 Divide a polynomial by a linear polynomial using synthetic division

We will bring down the 2, multiply 3 ● 2 = 6, and write the result in the middle row. Then we add.

cont’d
Multiply: 3 ● 2 = 6
Add: –7 + 6 = –1
We repeat this process of multiplying and then adding until the table is complete.
Multiply: 3(–1) = –3
Add: 0 + (–3) = –3
2 -7 0 5
3
2
6
-1
-3
-3

cont’d
cont’d
Multiply: 3(–3) = –9
Add: 5 + (–9) = –4
2 -7 0 5
3
2
6
-1
-3
-3
-9
-4

cont’d

1.4.3 Apply the factor theorem to factorize polynomials
The next theorem says that zeros of polynomials correspond to factors.

cont’d

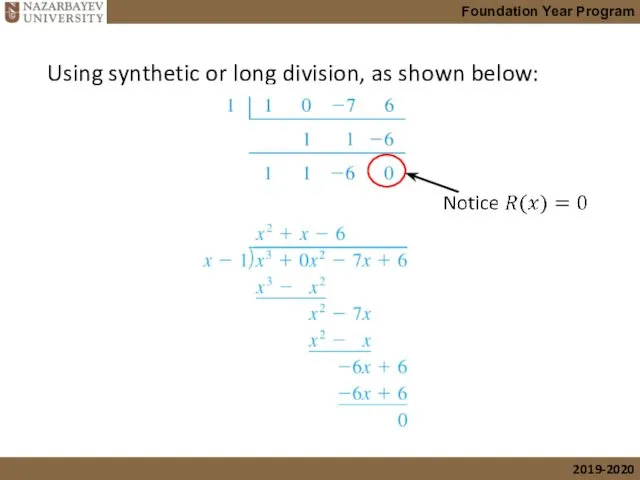
cont’d
Using synthetic or long division, as shown below:
cont’d

cont’d
Given polynomial
Using synthetic
or long division
Factor quadratic
x2 + x – 6

cont’d

cont’d
cont’d

Solution

cont’d
You can use the remainder theorem to find the remainder value:
1.4.4 Apply the remainder theorem to find the remainder

cont’d

cont’d
1 -1 1 5
-1
1
-1
-2
2
3
-3
2

cont’d
cont’d

cont’d
Solution

cont’d

cont’d

cont’d
Based on the previous exercise, we can state the following:
Remainder Theorem – version 2

Solution

Your turn!

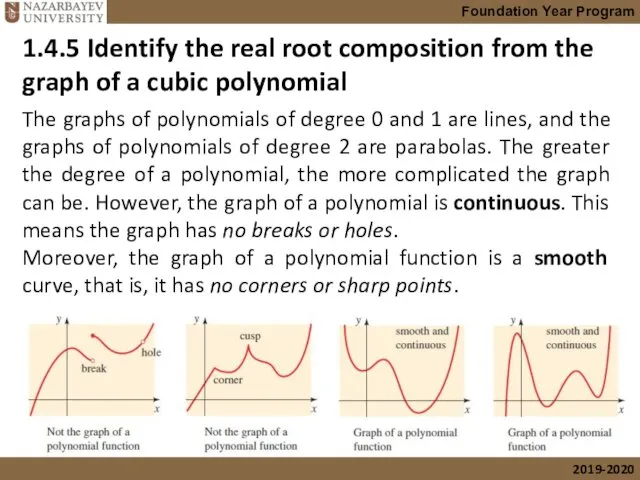
1.4.5 Identify the real root composition from the graph of a cubic polynomial
The graphs of polynomials of degree 0 and 1 are lines, and the graphs of polynomials of degree 2 are parabolas. The greater the degree of a polynomial, the more complicated the graph can be. However, the graph of a polynomial is continuous. This means the graph has no breaks or holes.
Moreover, the graph of a polynomial function is a smooth curve, that is, it has no corners or sharp points.

1.4.5 Identify the real root composition from the graph of a cubic polynomial
In this lecture we want to explore how the zeros of a cubic polynomial and their multiplicity affect the shape of the graph. In the next lecture you will learn basics of sketching a cubic polynomial.

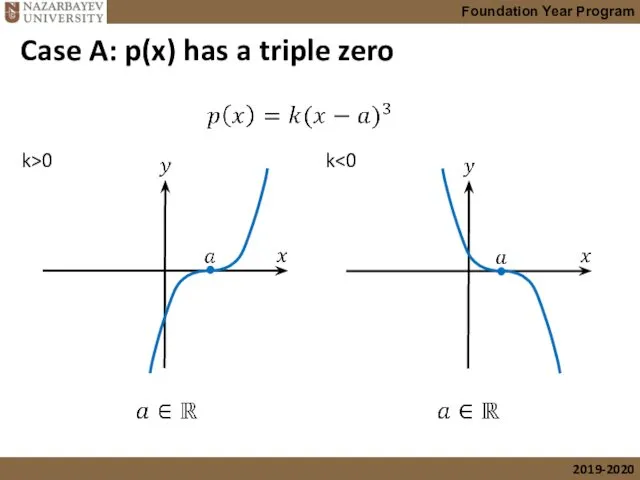
Case A: p(x) has a triple zero
k>0
k<0

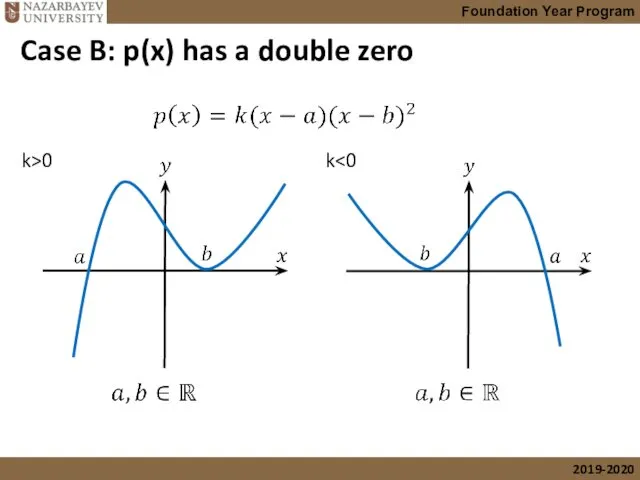
Case B: p(x) has a double zero
k>0
k<0

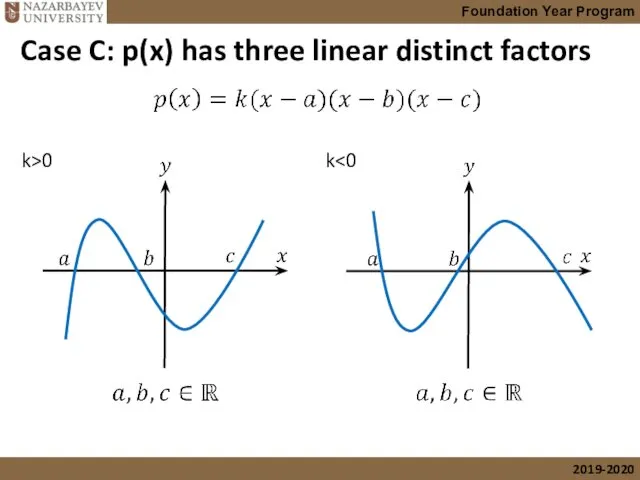
Case C: p(x) has three linear distinct factors
k>0
k<0

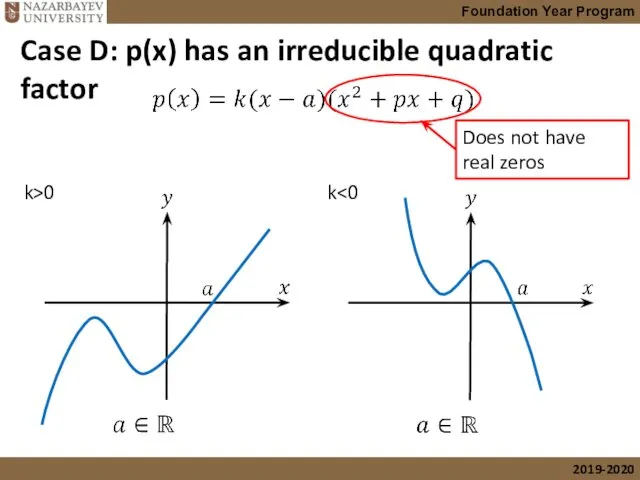
Case D: p(x) has an irreducible quadratic factor
k>0
k<0
Does not have real zeros

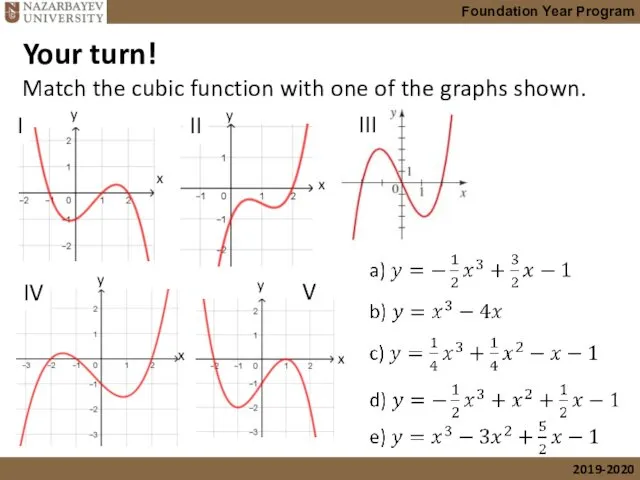
Your turn!
Match the cubic function with one of the graphs shown.
x
y
x
y
x
y
x
y
I
II
III
IV
V

1 -3 5/2 -1
2
1
2
-1
-2
1/2
1
0

Learning outcomes
1.4.1 Divide a polynomial by another polynomial using long division
1.4.2 Divide a polynomial by a linear polynomial using synthetic division
1.4.3 Apply the factor theorem to factorize polynomials
1.4.4 Apply the remainder theorem to find the remainder
1.4.5 Identify the real root composition from the graph of a cubic polynomial

Formulae