Содержание
- 2. Пример. Вычислить площадь фигуры, ограниченной линиями:
- 3. Решение: S
- 4. Находим координаты точки В: Тогда
- 5. 2 Пусть функция y=f(x) – неположительная и непрерывна на [a,b]. Отражая кривую y=f(x) относительно оси абсцисс,
- 6. Пример. Вычислить площадь фигуры, ограниченной линиями:
- 7. Решение:
- 8. SОАВ – это площадь над кривой ОАВ на отрезке [0;2]. Но эта кривая задается не одним
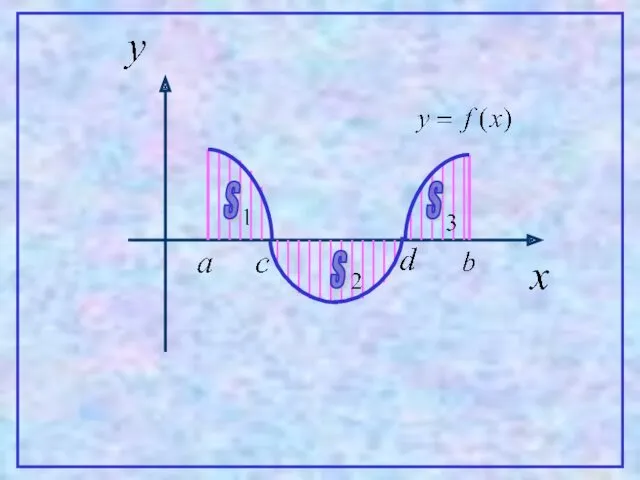
- 9. 3 Пусть функция y=f(x) – непрерывна на [a,b] и исходный отрезок можно разбить на определенное число
- 10. S S S
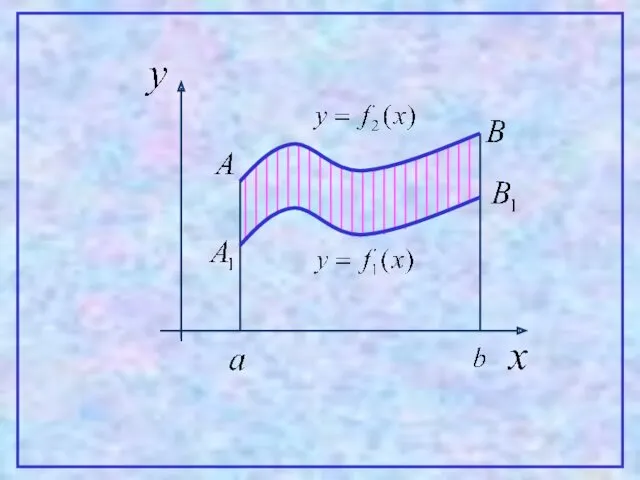
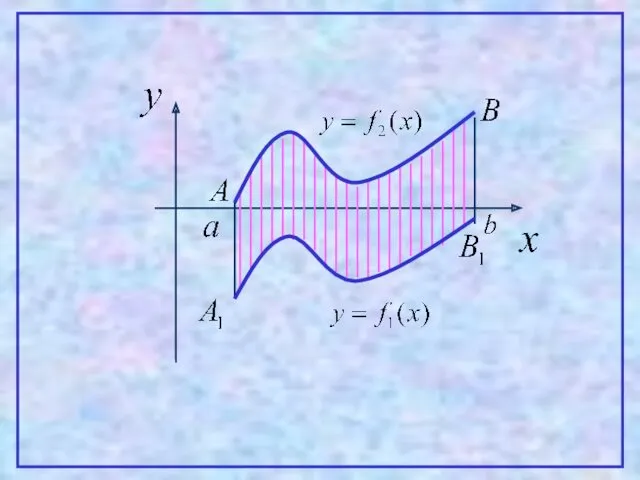
- 12. 4 Теорема. Пусть на [a,b] заданы непрерывные функции y=f1(x) и y=f2(x), такие что Тогда площадь фигуры,
- 13. Проиллюстрируем эту теорему графически. Рассмотрим несколько случаев. 1
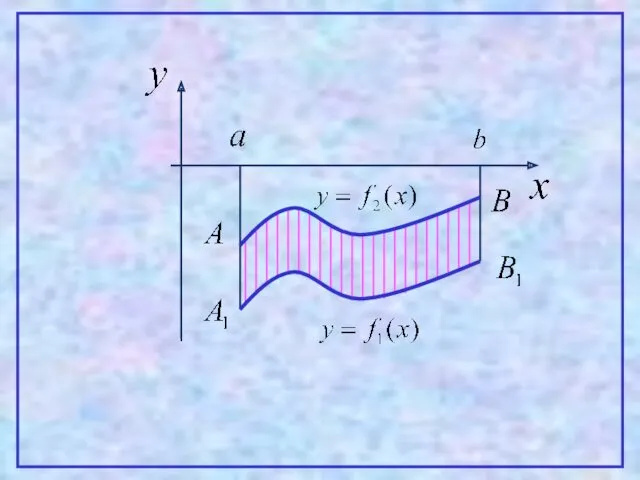
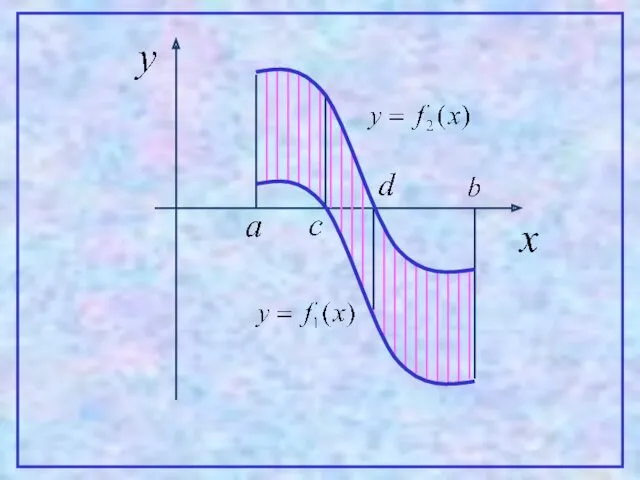
- 16. 2
- 19. 3
- 22. 4 Общий случай. Этот случай сводится к рассмотренным случаям 1-3, если разбить отрезок [a,b] на элементарные
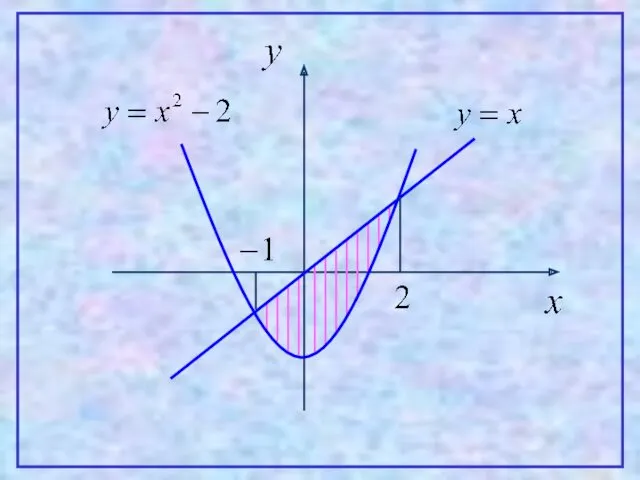
- 24. Пример. Вычислить площадь фигуры, ограниченной линиями:
- 26. Решение: Находим координаты точек пересечения линий: Следовательно, линии пересекаются в точках
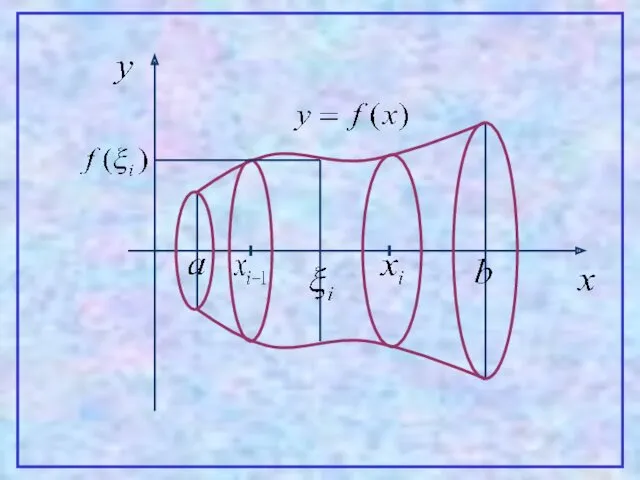
- 27. 2. Вычисление объемов тел вращения Пусть функция y=f(x) –знакопостоянная и непрерывна на [a,b]. Найти объем тела
- 29. Тогда некоторое приближение для искомого объема даст сумма Так как каждое слагаемое это объем цилиндра с
- 30. Правая часть выражения представляет собой предел интегральной суммы функции Поэтому
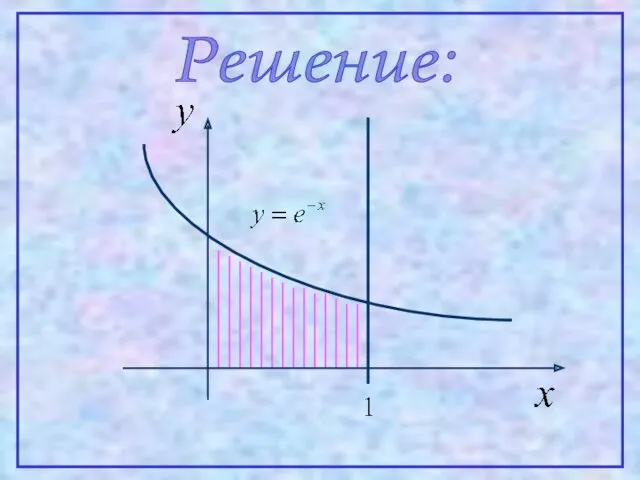
- 31. Пример. Вычислить объем тела, полученного от вращения вокруг оси абсцисс фигуры, ограниченной линиями:
- 32. Решение:
- 34. Если заменить х на у, то получим формулу для вычисления объема тела, полученного от вращения криволинейной
- 35. Пример. Вычислить объем тела, полученного от вращения вокруг оси ординат фигуры, ограниченной линиями:
- 36. Решение:
- 38. Скачать презентацию

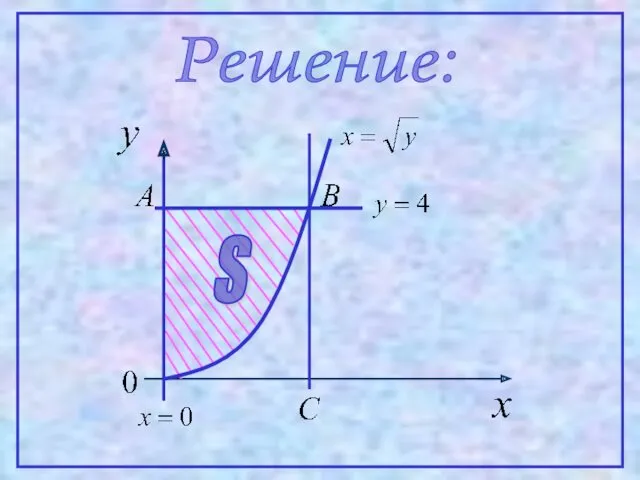

![2 Пусть функция y=f(x) – неположительная и непрерывна на [a,b].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/65191/slide-4.jpg)

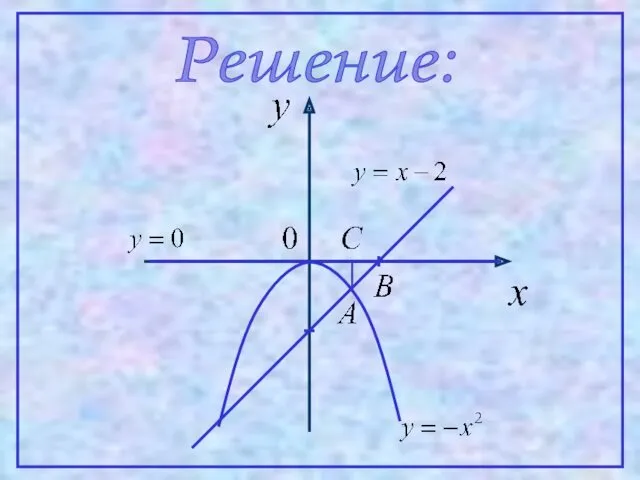
![SОАВ – это площадь над кривой ОАВ на отрезке [0;2].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/65191/slide-7.jpg)
![3 Пусть функция y=f(x) – непрерывна на [a,b] и исходный](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/65191/slide-8.jpg)
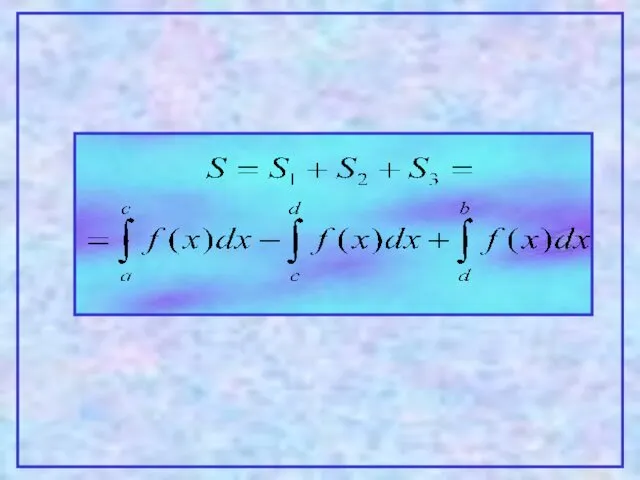
![4 Теорема. Пусть на [a,b] заданы непрерывные функции y=f1(x) и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/65191/slide-11.jpg)

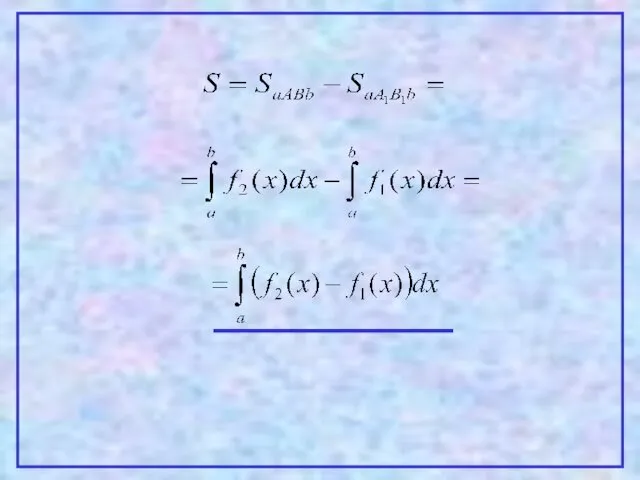

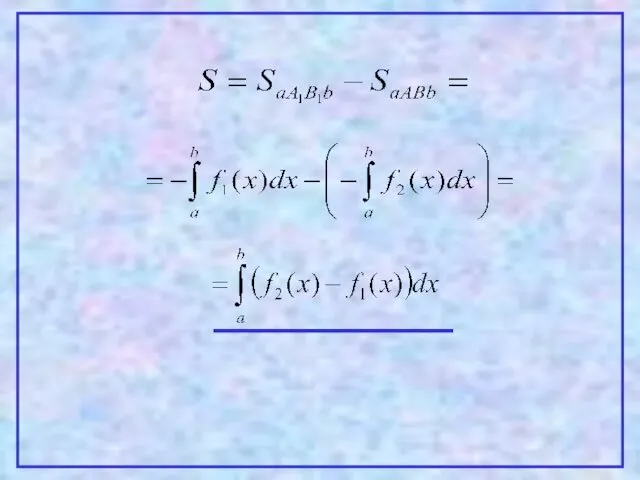

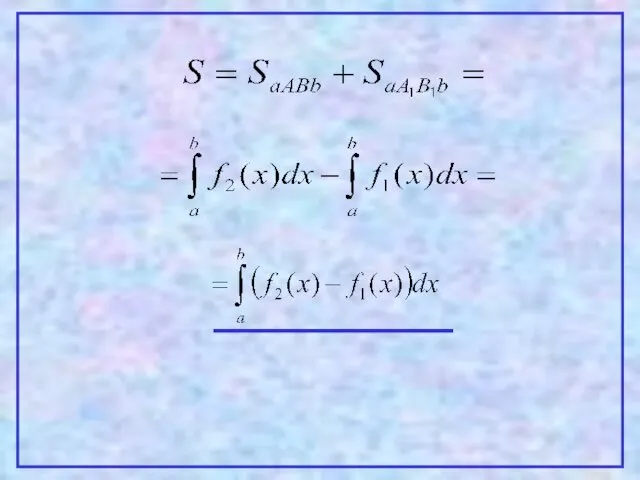







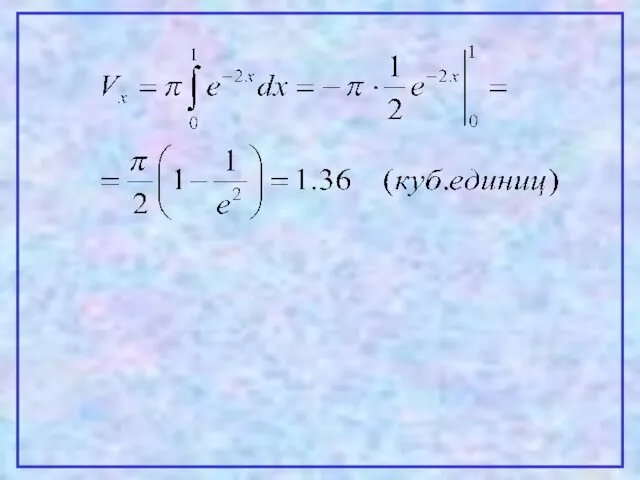


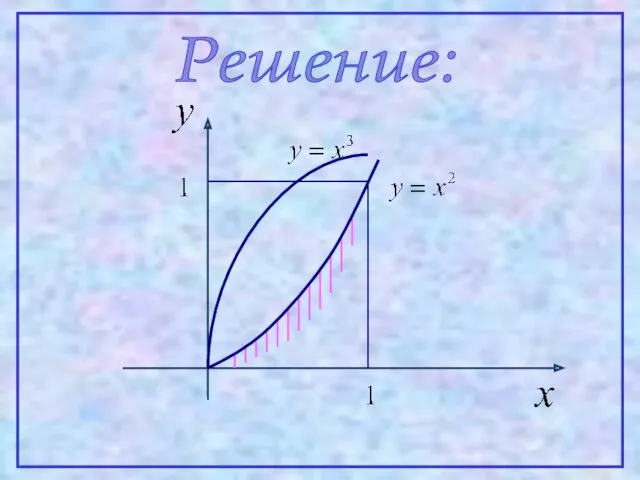
 Электроника
Электроника Гуманизм: абстрактный или классовый, по роману А.А. Фадеева Разгром
Гуманизм: абстрактный или классовый, по роману А.А. Фадеева Разгром Государство на берегу Нила
Государство на берегу Нила Правила безопасности в Интернете
Правила безопасности в Интернете Бурятская полугрубошерстная порода овец
Бурятская полугрубошерстная порода овец Контрольная работа Устройство православного храма
Контрольная работа Устройство православного храма Нормативное регулирование учета денежных средств
Нормативное регулирование учета денежных средств Социальная структура и социальные отношения
Социальная структура и социальные отношения Задание В1. Тренажер
Задание В1. Тренажер Государство и право Российской империи в XVIII веке
Государство и право Российской империи в XVIII веке Татьянин день
Татьянин день Аменорея. Гипоменструалді синдром. Жағдайында диагностикалау және емдеу принциптері
Аменорея. Гипоменструалді синдром. Жағдайында диагностикалау және емдеу принциптері История создания мыла
История создания мыла Storage devices
Storage devices СРС: Составление алгоритмов оказания неотложной доврачебной помощи
СРС: Составление алгоритмов оказания неотложной доврачебной помощи Урок по теме:ГТО
Урок по теме:ГТО Электрические схемы КЭС
Электрические схемы КЭС Анализ вакансий, заявленных работодателями в органы службы занятости населения Ханты-Мансийского автономного округа – Югры
Анализ вакансий, заявленных работодателями в органы службы занятости населения Ханты-Мансийского автономного округа – Югры Правила прийняття інвестиційних рішень. (Тема 7)
Правила прийняття інвестиційних рішень. (Тема 7) Кодирование текстовой информации
Кодирование текстовой информации Жидкокристаллический индикатор (ЖКИ-LCD). Лекция 6
Жидкокристаллический индикатор (ЖКИ-LCD). Лекция 6 Отчет о занятиях по программе Мы – поколение будущего!
Отчет о занятиях по программе Мы – поколение будущего! Речные рыбы. Презентация.
Речные рыбы. Презентация. Роль воды в жизни растений. Проращивание семян
Роль воды в жизни растений. Проращивание семян Тренажер. Сложение в пределах 20 с переходом через разряд № 1
Тренажер. Сложение в пределах 20 с переходом через разряд № 1 Развитие общей выносливости. Средства и методы
Развитие общей выносливости. Средства и методы Трансформаторы
Трансформаторы Энергосбережение в зданиях. Практическое занятие. Системы освещения и нагрузки в системах электроснабжения зданий и сооружений
Энергосбережение в зданиях. Практическое занятие. Системы освещения и нагрузки в системах электроснабжения зданий и сооружений