Содержание
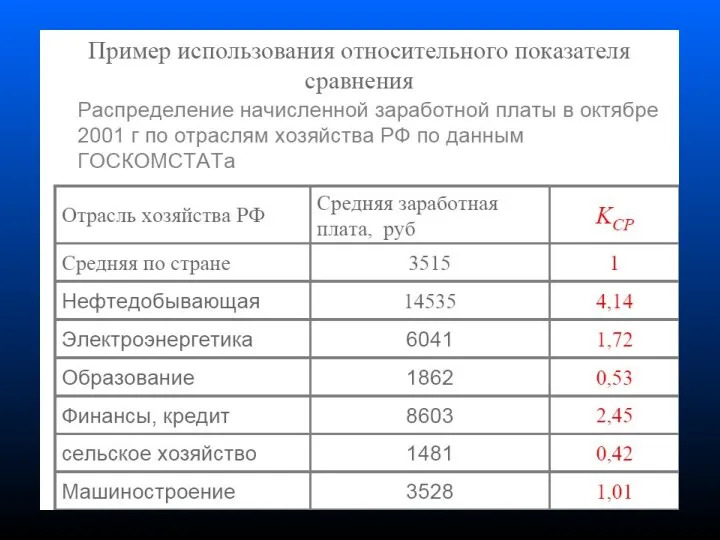
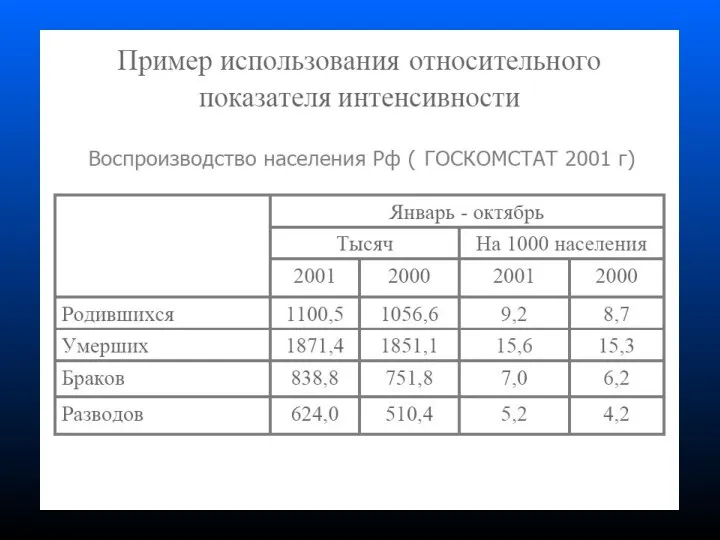
- 16. 1 Относительные и абсолютные показатели
- 35. 2 Статистические показатели, используемые для характеристики рядов распределений. Виды средних.
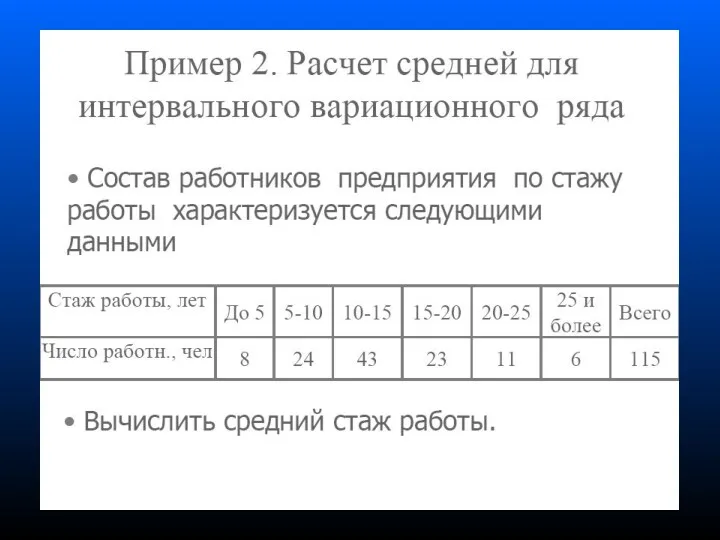
- 36. Статистические показатели вариационного ряда 1. Среднее значение, мода, медиана - характеризуют наиболее типичные значения признака 2.
- 43. xi
- 51. 3 Медиана и мода
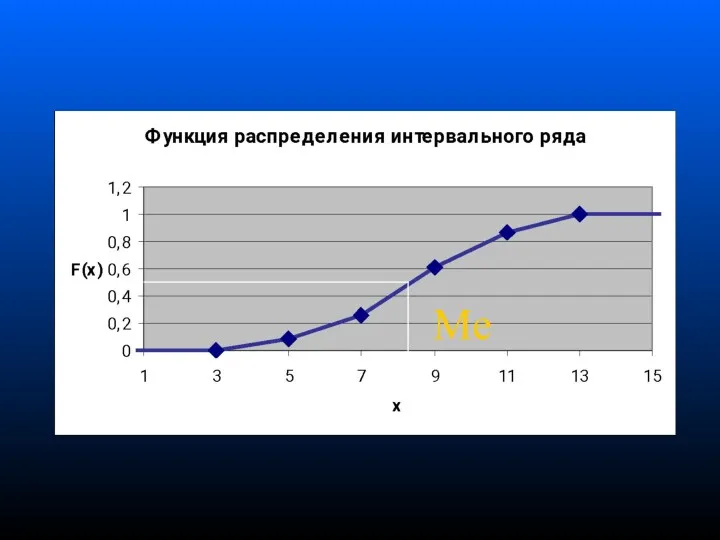
- 52. Медиана распределения - значение признака, которое приходится на середину ранжированной статистической совокупности Признаку, определяющий медиану дискретного
- 53. Me
- 55. Дискретный ряд xi fi Середина совокупности приходится на 48 по счету квартиру (95/2=47.5). В этой квартире
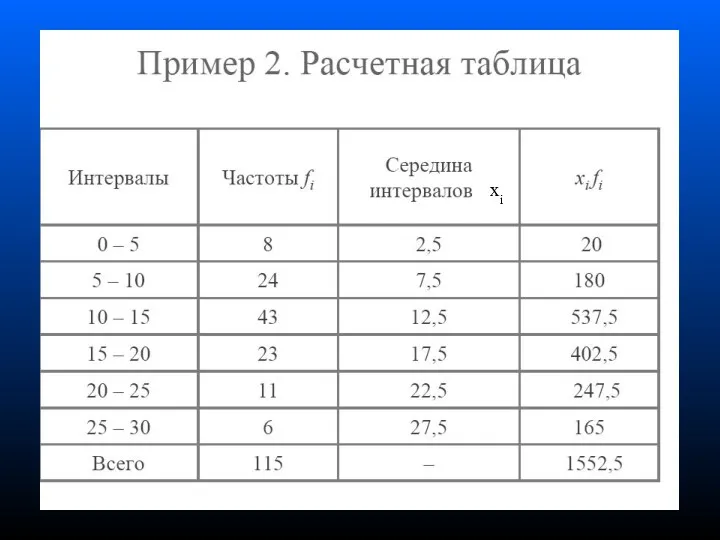
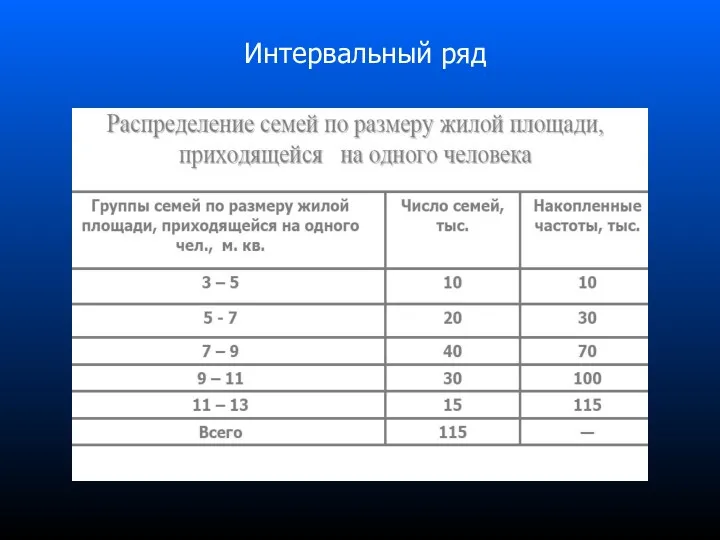
- 56. Интервальный ряд
- 57. Середина совокупности приходится на 57500-ю семью (115/2=57.5). Медианный интервал (на котором накопленная частота впервые превышает 115/2
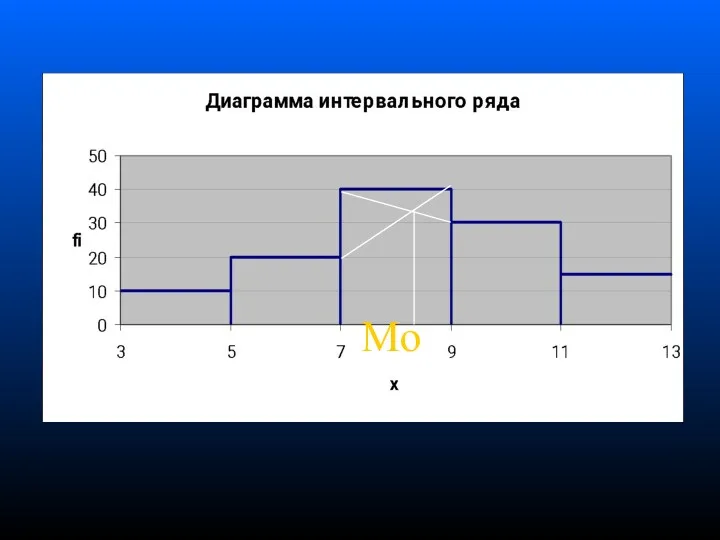
- 59. Mo
- 60. Модальным является интервал (7-9) Mo= 7+(40-20)/(40-20+40-30) .2
- 61. 5.4. Показатели вариации
- 62. Размах вариации Размах вариации R = xmax - xmin показывает, насколько велико различие между максимальным и
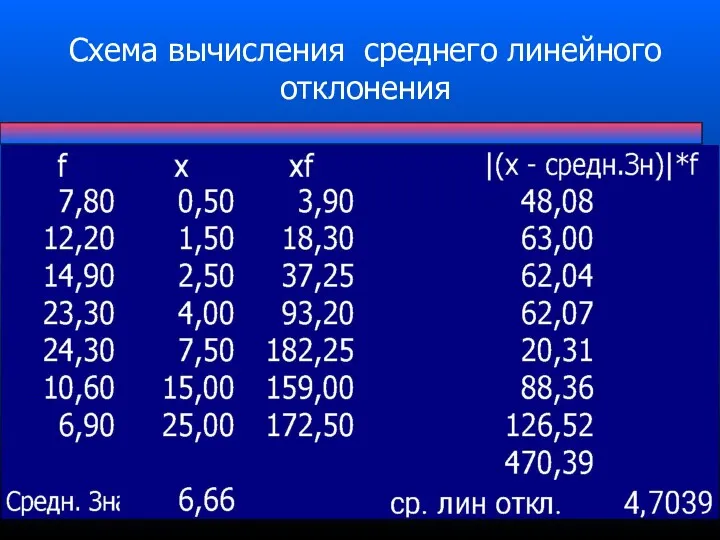
- 63. Среднее линейное отклонение Важной структурной характеристикой вариационного ряда является среднее линейное отклонение, которое вычисляется по формулам
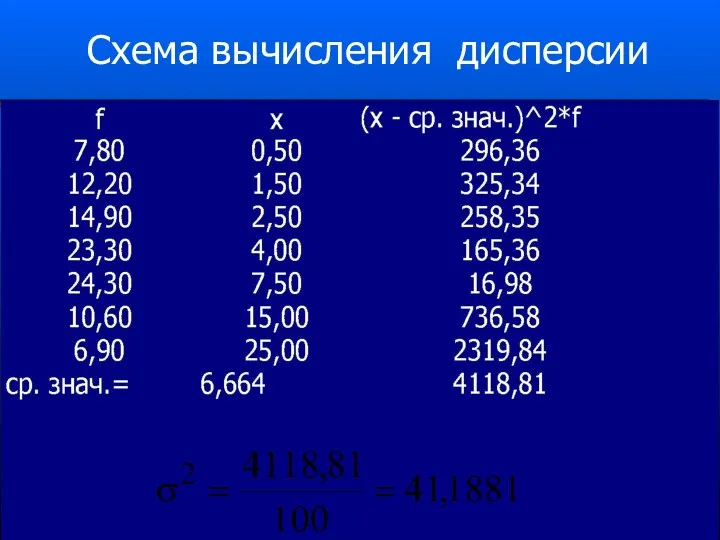
- 64. Дисперсия Дисперсия характеризует степень рассеяния индивидуальных значений признака в совокупности от среднего значения и вычисляется по
- 65. Взвешенная дисперсия В этом случае (взвешенная дисперсия) вариационный ряд предполагается сгруппированным и суммирование ведется по всем
- 66. Среднее квадратическое отклонение Среднее квадратическое отклонение представляет собой характеристику вариационного ряда, которая отражает рассеянность членов совокупности
- 67. Другие показатели вариации Коэффициент осцилляции VR Линейный коэффициент вариации Vd Коэффициент вариации
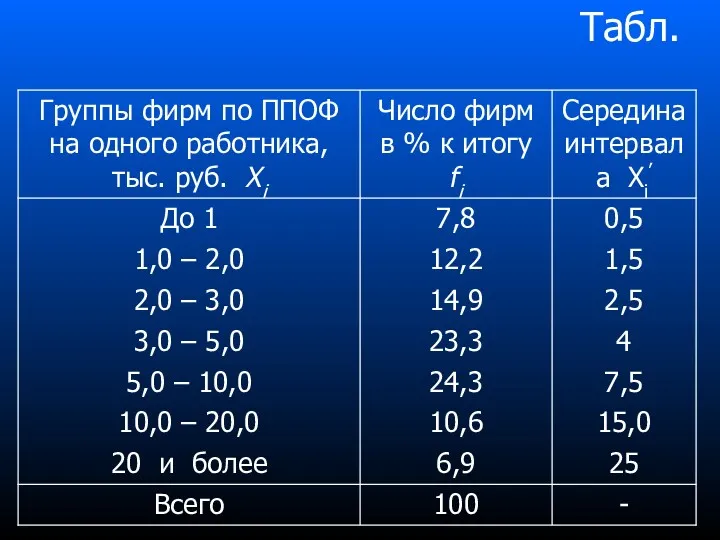
- 68. Пример вычисления показателей вариации Рассмотрим вычисление среднего линейного отклонения, дисперсии и среднеквадратичного отклонения для интервального ряда
- 69. Табл.
- 70. Вычисление дисперсии в случае интервального ряда В случае интервального ряда в качестве значения вариационного признака xi
- 71. Схема вычисления среднего линейного отклонения
- 72. Схема вычисления дисперсии
- 73. 6. Эмпирическое определение тесноты корреляционной связи. Правило сложения дисперсий.
- 74. Рассмотрим аналитическую группировку данных по двум признакам. По первому признаку (группировочный или факторный признак) мы разобьем
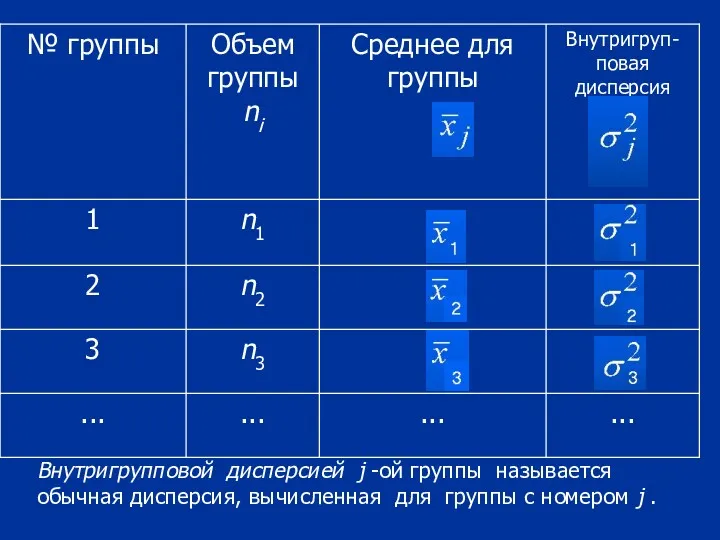
- 75. Внутригрупповой дисперсией j -ой группы называется обычная дисперсия, вычисленная для группы с номером j .
- 76. где xij - значения вариант, fij - частот, - среднее значение , а - объем для
- 77. По имеющимся данным можно вычислить общее среднее:
- 78. Межгрупповая дисперсия Межгрупповой дисперсией называется дисперсия групповых средних, рассчитанная с учетом объема каждой группы nj
- 79. Средняя из групповых дисперсий. Формула сложения дисперсий В математической статистике показано, что между общей дисперсией, межгрупповой
- 80. Эмпирическое корреляционное отношение - количественная характеристика тесноты связи факторного и результативного признаков - равно корню квадратному
- 81. По величине эмпирического корреляционного отношения можно определить, насколько сильно связаны факторный и результативный признаки. 0-0.3 связь
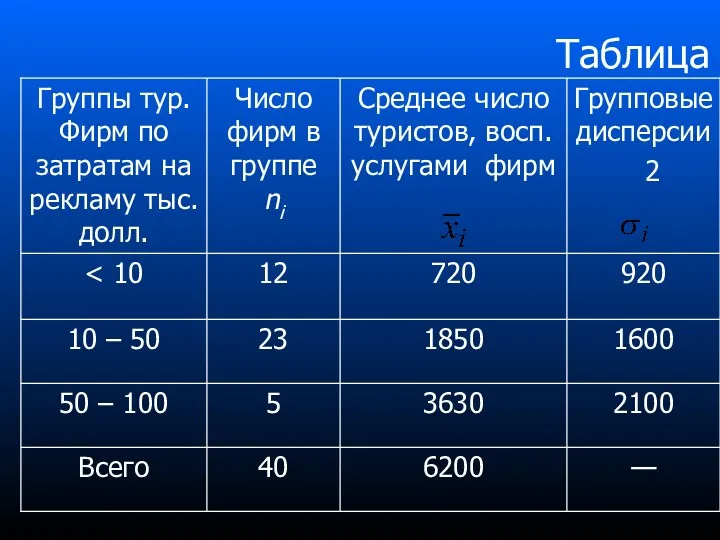
- 82. Пример решения задачи Задача. По данным таблицы (см. след слайд) вычислить общую дисперсию, а также характеризовать
- 83. Таблица
- 84. Решение задачи 1. Вычисляем среднее значение 2. Найдем среднюю групповую дисперсию
- 85. 3. Вычислим межгрупповую дисперсию 4. Общая дисперсия равна
- 86. Сделаем выводы Средняя из групповых дисперсий значительно меньше межгрупповой дисперсии. Это значит, что группы существенно отличаются
- 87. 7. Альтернативный признак. Среднее значение и дисперсия. Эмпирическая оценка тесноты связи в случае альтернативного признака.
- 88. Рассмотрим вариационный ряд с двумя возможными значениями признака (альтернативный признак) Пусть p - доля единиц совокупности,
- 89. Вычисление среднего значения и дисперсии Среднее значение и дисперсия такого ряда вычисляется по формулам:
- 90. Внутригрупповая и межгрупповая дисперсии для альтернативного признака Пусть имеется аналитическая группировка, включающая несколько групп, характеризуемых альтернативным
- 91. Внутригрупповая дисперсия и среднегрупповая дисперсии определяются по формулам:
- 92. Формула межгрупповой дисперсии имеет вид (p - доля признака во всей совокупности, она же - общее
- 93. Общая дисперсия вычисляется по формуле Как и в случае рядов, построенных по количественному признаку, справедлива формула
- 94. Пример вычисления дисперсий доли Данные об удельном весе рабочих основных специальностей в трех цехах предприятия представлены
- 95. Найдем среднюю долю основных рабочих Вычислим общую дисперсию
- 96. Средняя из групповых дисперсий Вычислим внутригрупповые дисперсии
- 97. Проверяем вычисления, используя формулу сложения дисперсии Найдем межгрупповую дисперсию
- 99. Скачать презентацию
















































































 Великие русские химики
Великие русские химики Действие магнитного поля на проводник с током
Действие магнитного поля на проводник с током Саванны и редколесья
Саванны и редколесья Рисуем цветы
Рисуем цветы Виды шовного материала. Техника вязания узлов
Виды шовного материала. Техника вязания узлов Стандартные изделия в строительстве и примеры типизации их размеров
Стандартные изделия в строительстве и примеры типизации их размеров Представление (кодирование) чисел. Информатика для колледжа
Представление (кодирование) чисел. Информатика для колледжа Люди и еда: психологические аспекты пищевого поведения
Люди и еда: психологические аспекты пищевого поведения Профессии, связанные с обработкой древесины. Пороки древесины
Профессии, связанные с обработкой древесины. Пороки древесины TPMS Introduction (v.2)
TPMS Introduction (v.2) Теории и модели перевода. Лекция 3
Теории и модели перевода. Лекция 3 Задачи теории расписаний
Задачи теории расписаний Селищенский центр народного творчества и досуга
Селищенский центр народного творчества и досуга Презентация к мастер-классу
Презентация к мастер-классу Глібчук Руслана. Моє життєве кредо
Глібчук Руслана. Моє життєве кредо Театр сквозь годы и века Третьяк Л.М.2
Театр сквозь годы и века Третьяк Л.М.2 6 класс. Гидросфера 2 урок. Части мирового океана
6 класс. Гидросфера 2 урок. Части мирового океана Урок Реакции ионного обмена
Урок Реакции ионного обмена Организация работы классного руководителя и воспитателя в свете национальной инициативы Наша новая школа
Организация работы классного руководителя и воспитателя в свете национальной инициативы Наша новая школа Результаты диагностики речевого развития учащихся 1х классов.
Результаты диагностики речевого развития учащихся 1х классов. Бытовые приборы
Бытовые приборы Замена пролетных строений консольными кранами
Замена пролетных строений консольными кранами Социальная сфера
Социальная сфера Схема образования облака
Схема образования облака Тренинг Доверие
Тренинг Доверие Материалы мастер-класса ИКТ на уроках в начальной школе
Материалы мастер-класса ИКТ на уроках в начальной школе Расчёт стоимости ремонтных работ спортивного комплекса г. Коркино. Практика
Расчёт стоимости ремонтных работ спортивного комплекса г. Коркино. Практика Презентация для проверки определений по педагогическому речеведению.
Презентация для проверки определений по педагогическому речеведению.