Слайд 2

Karnaugh maps
We will describe a procedure simplifying sum-of-products expansions.
The goal of
this procedure is to produce Boolean sums of Boolean products that represent a Boolean function with the fewest products of literals such that these products contain the fewest literals possible among all sums of products that represent a Boolean function.
Finding such a sum of products is called minimization of the Boolean function.
Слайд 3
Karnaugh maps
The procedure we will introduce, known as Karnaugh maps (or
K-maps), was designed in the 1950s.
Слайд 4

Karnaugh maps
To reduce the number of terms in a Boolean expression
it is necessary to find terms to combine.
There is a graphical method, called a Karnaugh map or K-map, for finding terms to combine for Boolean functions involving a relatively small number of variables.
The method we will describe was introduced by Maurice Karnaugh in 1953.
His method is based on earlier work by E. W. Veitch. (This method is usually applied only when the function involves six or fewer variables.)
Слайд 5

Karnaugh maps
MAURICE KARNAUGH (BORN 1924)
Maurice Karnaugh, born in New York
City, received his B.S. from the City College of New York and his M.S. and Ph.D. from Yale University.
Слайд 6

Karnaugh maps
He was a member of the technical staff at Bell
Laboratories from 1952 until 1966 and Manager of Research and Development at the Federal Systems Division of AT&T from 1966 to 1970.
Слайд 7

Karnaugh maps
In 1970 he joined IBM as a member of the
research staff.
Слайд 8

Karnaugh maps
Karnaugh has made fundamental contributions to the application of digital
techniques in both computing and telecommunications.
His current interests include knowledge-based systems in computers and heuristic search methods.
Слайд 9

Karnaugh maps
K-maps give us a visual method for simplifying sum-of-products expansions;
they are not suited for mechanizing this process.
We will first illustrate how K-maps are used to simplify expansions of Boolean functions in two variables.
We will continue by showing how K-maps can be used to minimize Boolean functions in three variables and then in four variables.
Слайд 10

Karnaugh maps in two variables
Слайд 11

Karnaugh maps in two variables
Слайд 12
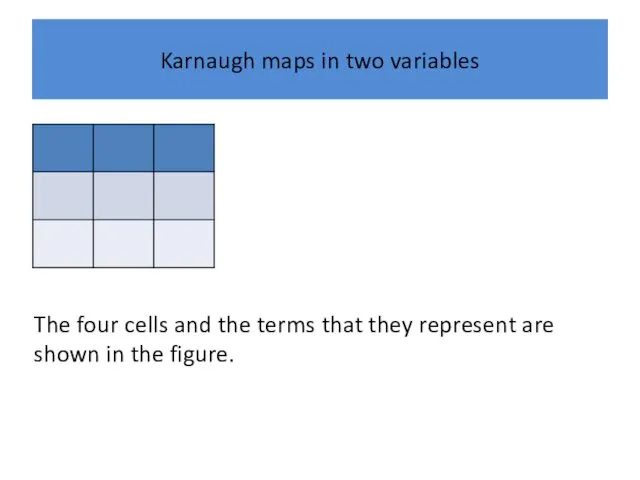
Karnaugh maps in two variables
The four cells and the terms that
they represent are shown in the figure.
Слайд 13
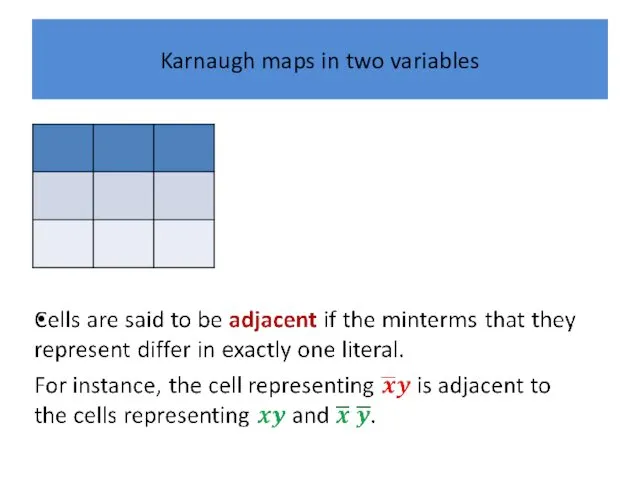
Karnaugh maps in two variables
Слайд 14
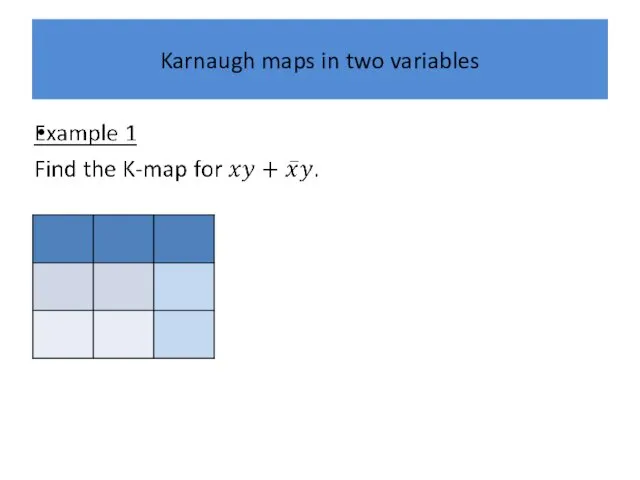
Karnaugh maps in two variables
Слайд 15
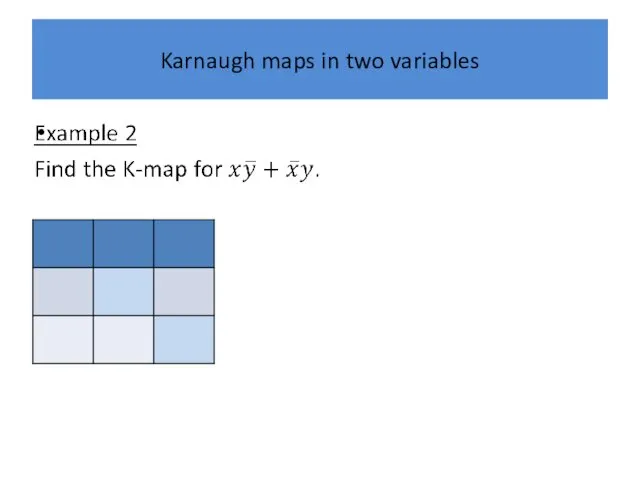
Karnaugh maps in two variables
Слайд 16
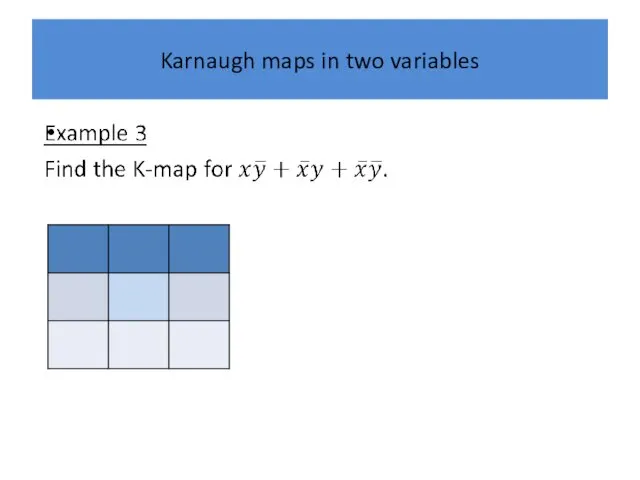
Karnaugh maps in two variables
Слайд 17

Karnaugh maps in two variables
Слайд 18

Karnaugh maps in two variables
Слайд 19
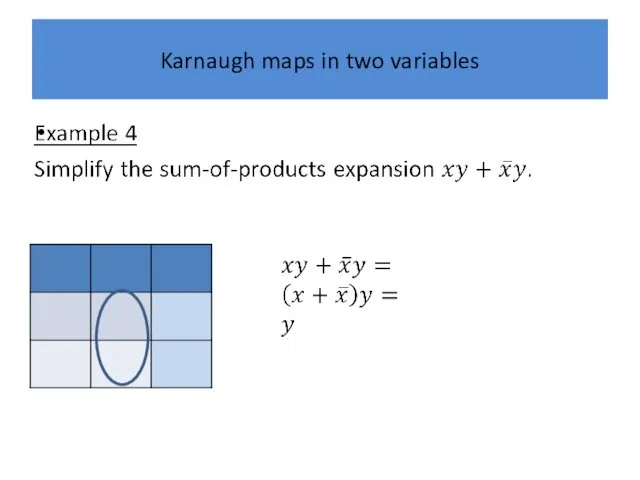
Karnaugh maps in two variables
Слайд 20
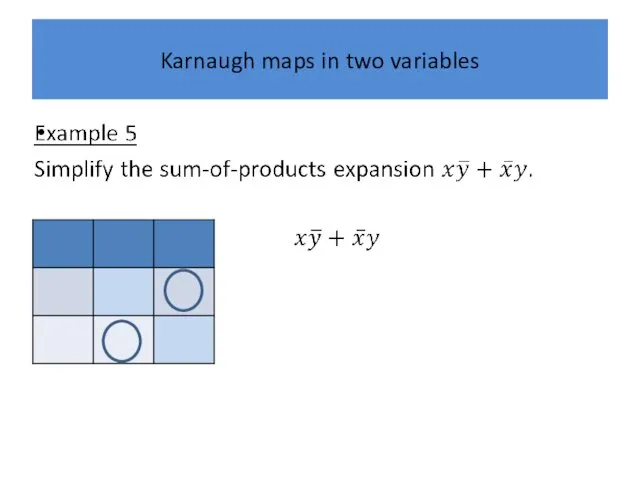
Karnaugh maps in two variables
Слайд 21
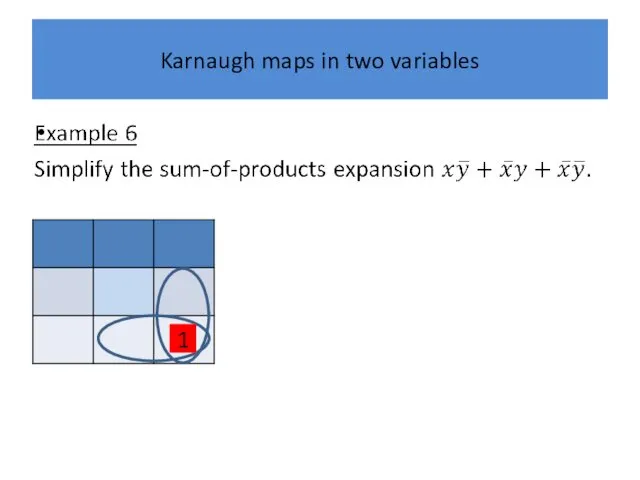
Karnaugh maps in two variables
1
Слайд 22
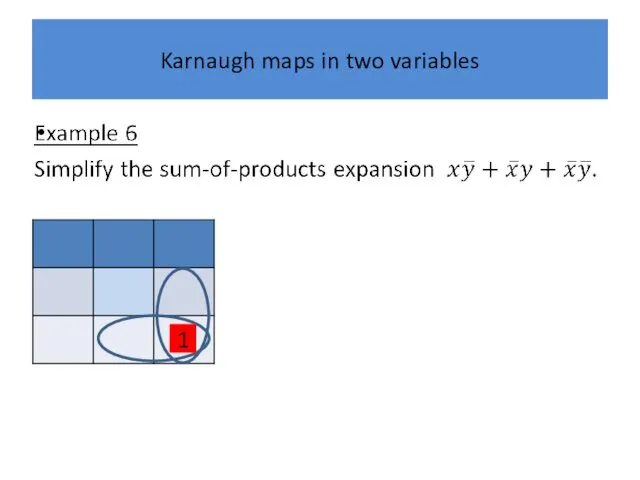
Karnaugh maps in two variables
1
Слайд 23
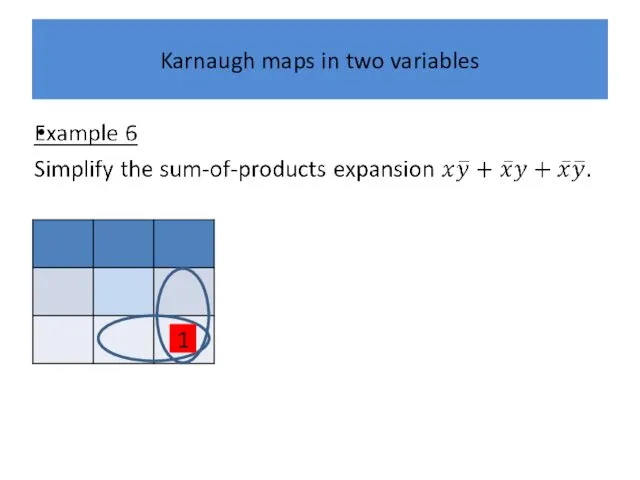
Karnaugh maps in two variables
1
Слайд 24
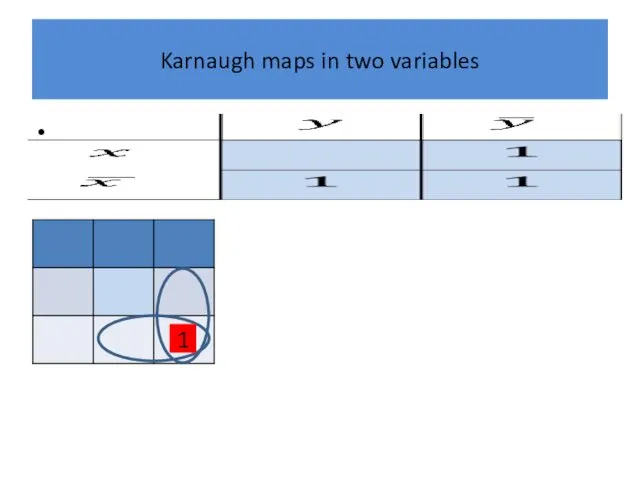
Karnaugh maps in two variables
1
Слайд 25
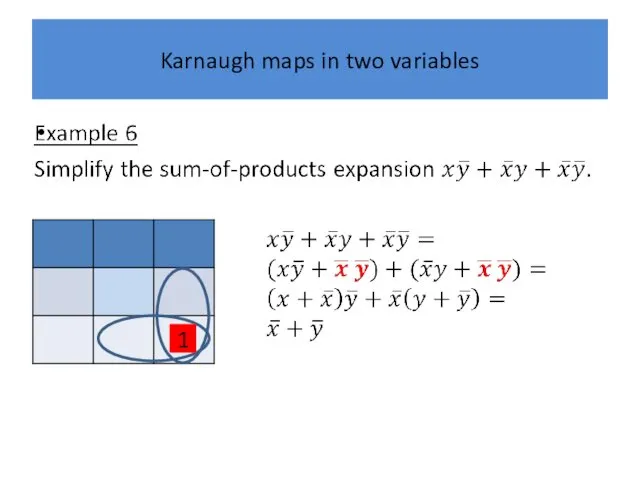
Karnaugh maps in two variables
1
Слайд 26
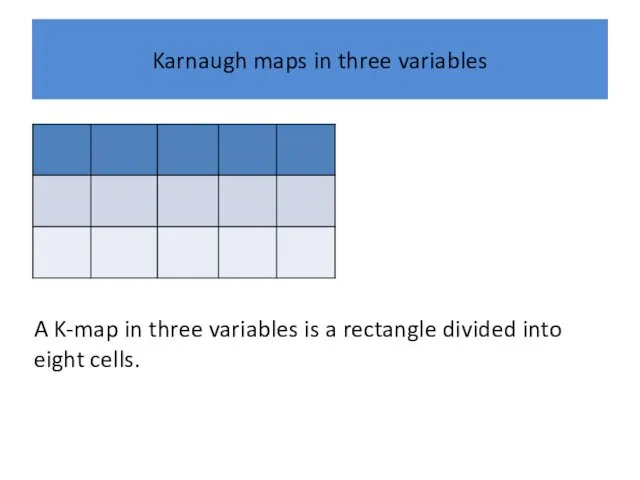
Karnaugh maps in three variables
A K-map in three variables is a
rectangle divided into eight cells.
Слайд 27
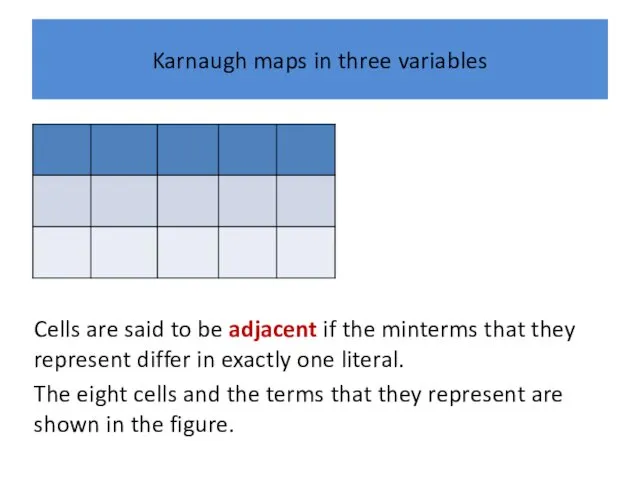
Karnaugh maps in three variables
Cells are said to be adjacent if
the minterms that they represent differ in exactly one literal.
The eight cells and the terms that they represent are shown in the figure.
Слайд 28
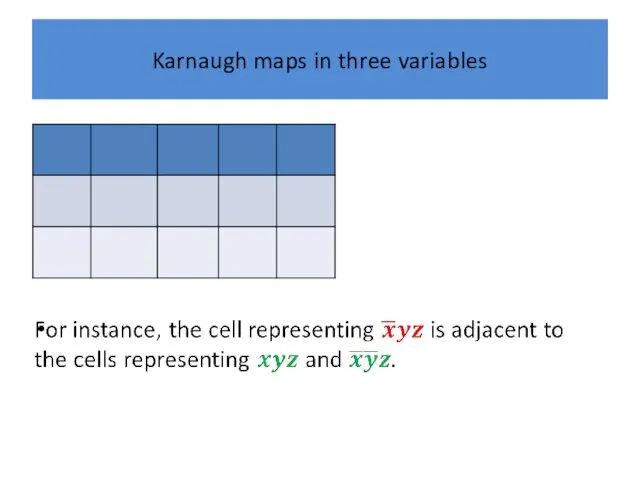
Karnaugh maps in three variables
Слайд 29
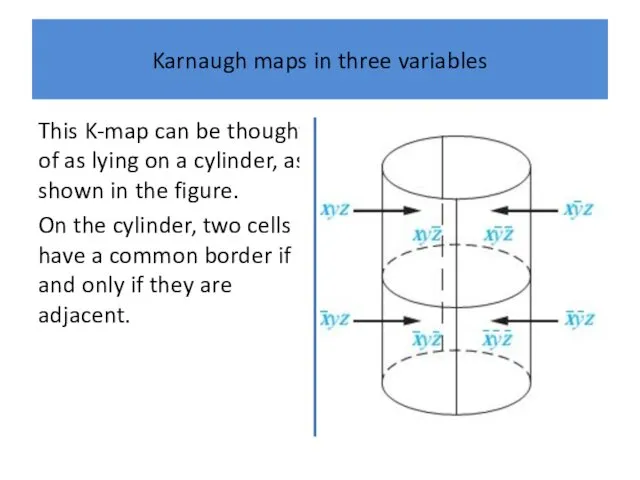
Karnaugh maps in three variables
This K-map can be thought of as
lying on a cylinder, as shown in the figure.
On the cylinder, two cells have a common border if and only if they are adjacent.
Слайд 30
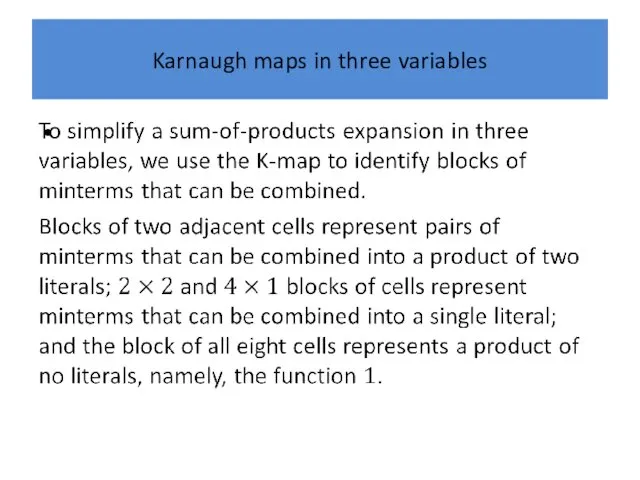
Karnaugh maps in three variables
Слайд 31

Karnaugh maps in three variables
Слайд 32

Karnaugh maps in three variables
Слайд 33

Karnaugh maps in three variables
Слайд 34

Karnaugh maps in three variables
Слайд 35
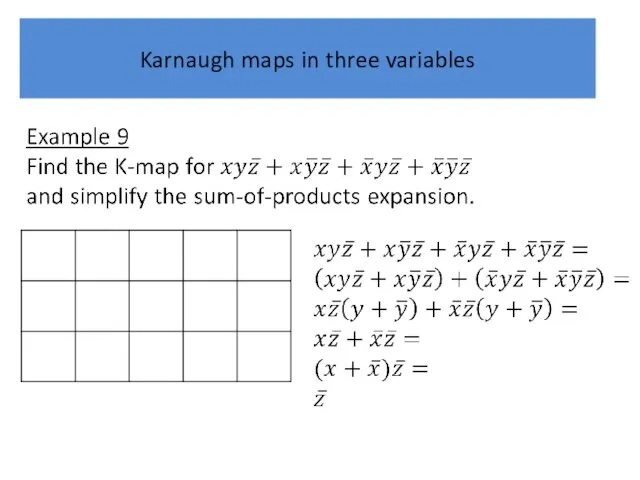
Karnaugh maps in three variables
Слайд 36
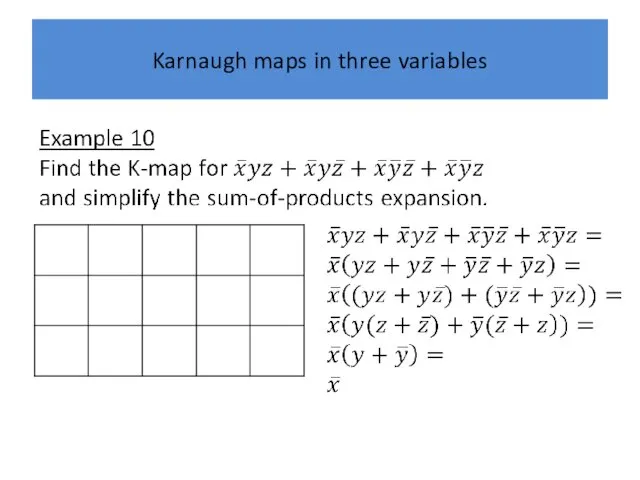
Karnaugh maps in three variables
Слайд 37
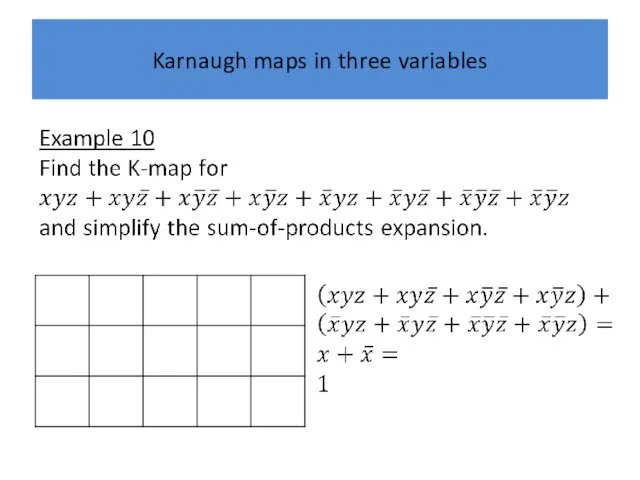
Karnaugh maps in three variables
Слайд 38
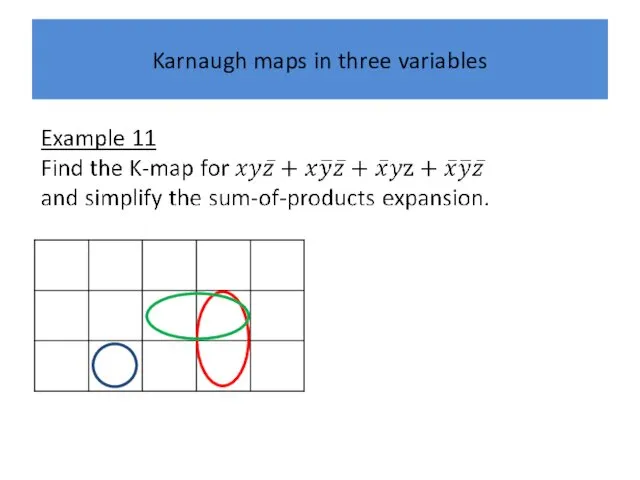
Karnaugh maps in three variables
Слайд 39
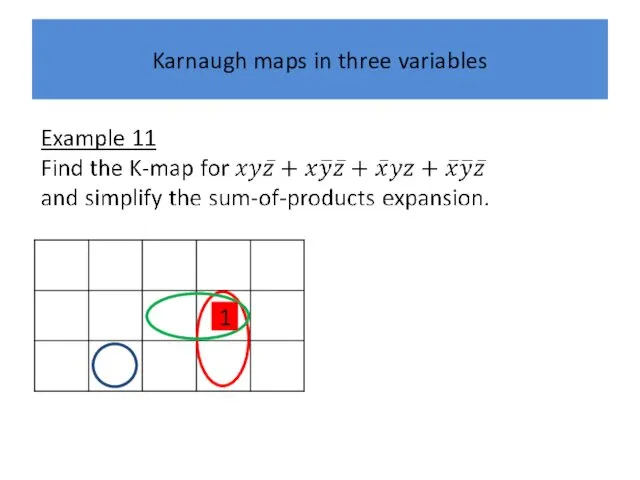
Karnaugh maps in three variables
1
Слайд 40
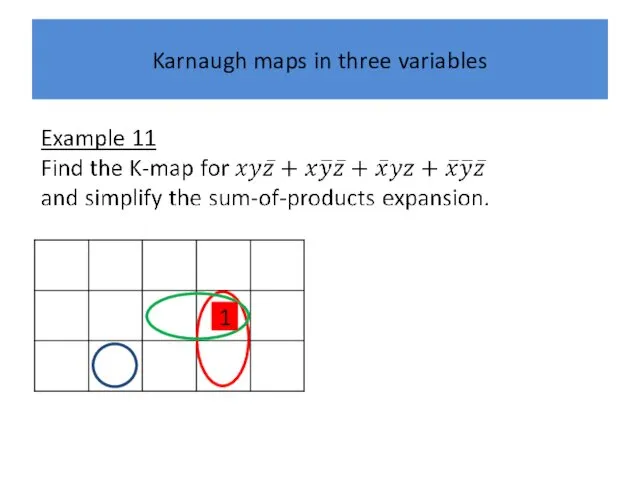
Karnaugh maps in three variables
1
Слайд 41
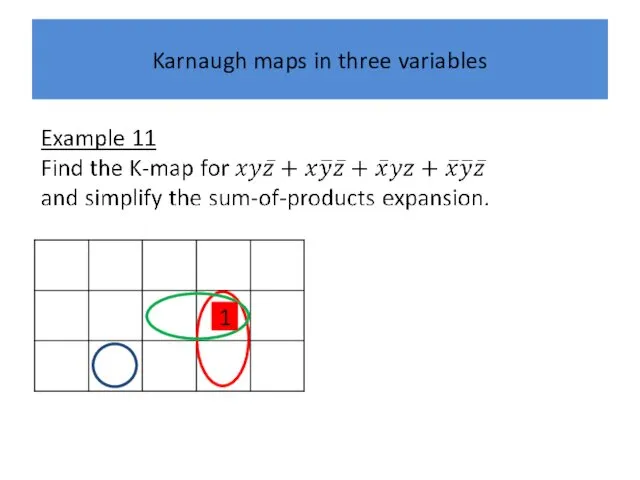
Karnaugh maps in three variables
1
Слайд 42
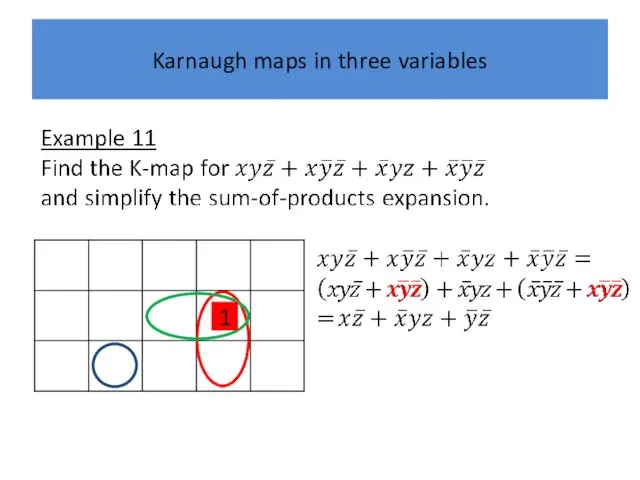
Karnaugh maps in three variables
1
Слайд 43
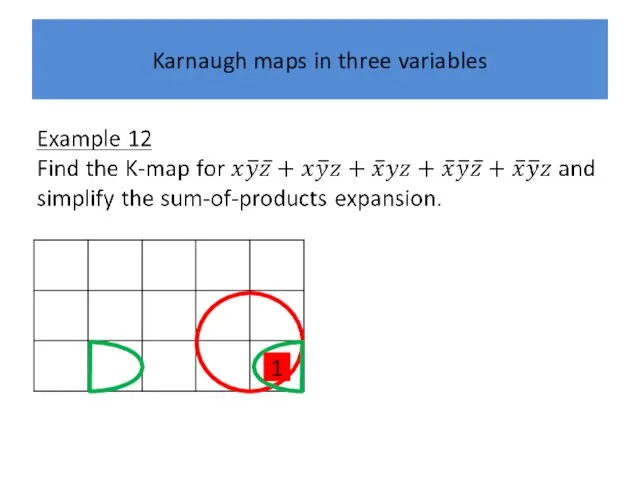
Karnaugh maps in three variables
1
Слайд 44
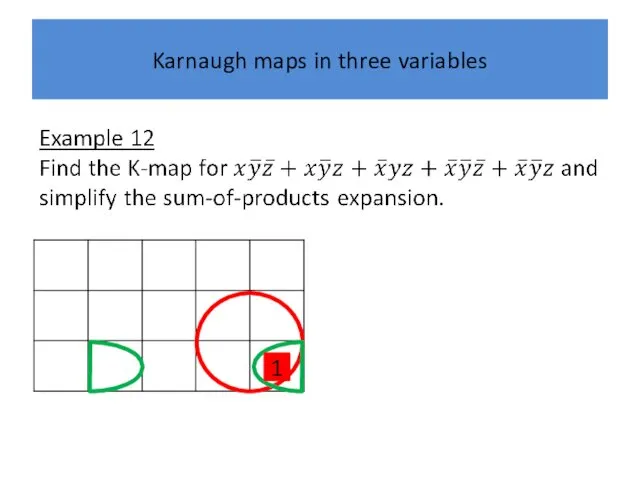
Karnaugh maps in three variables
1
Слайд 45
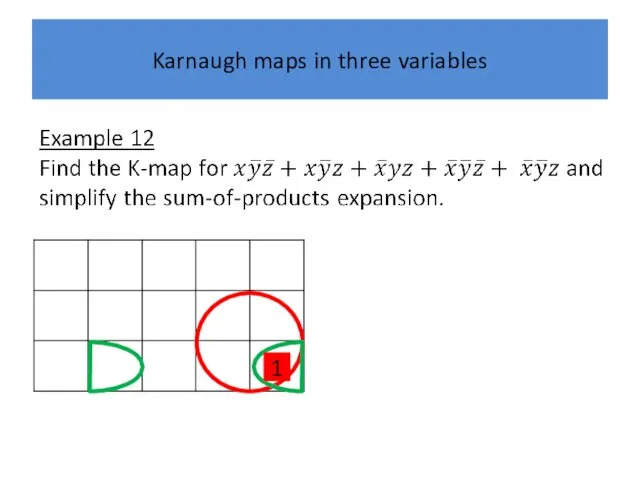
Karnaugh maps in three variables
1
Слайд 46
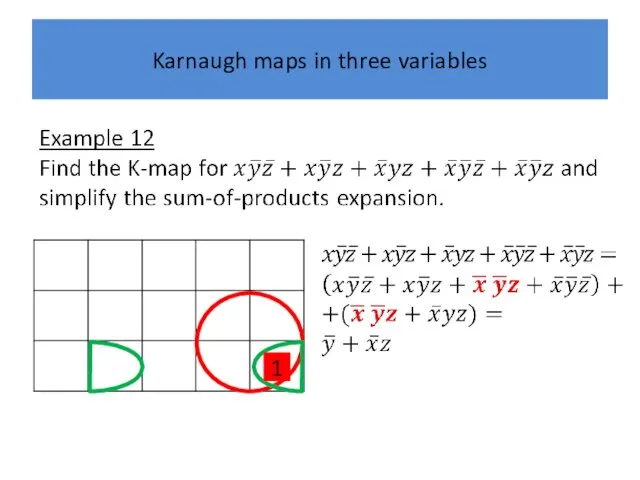
Karnaugh maps in three variables
1
Слайд 47
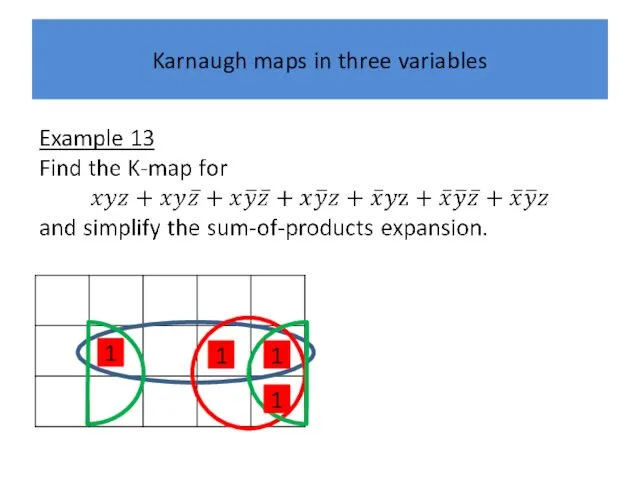
Karnaugh maps in three variables
1
1
1
1
Слайд 48
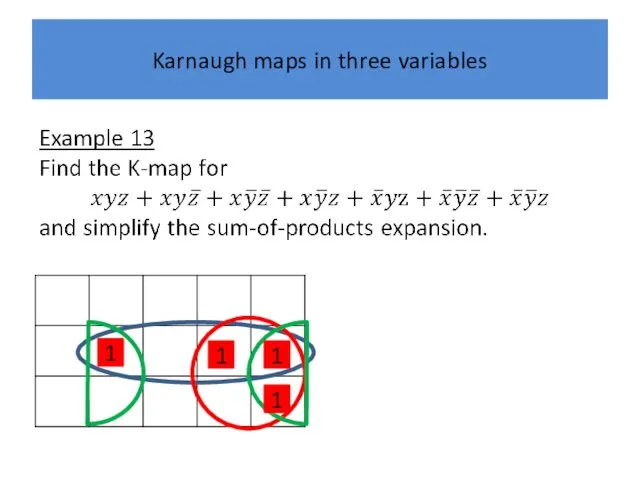
Karnaugh maps in three variables
1
1
1
1
Слайд 49
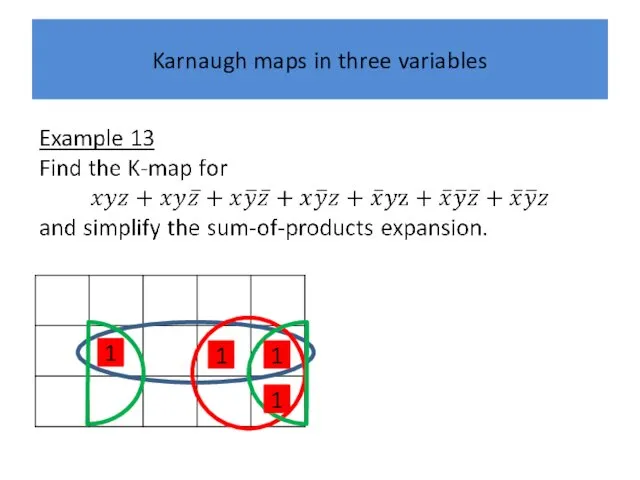
Karnaugh maps in three variables
1
1
1
1
Слайд 50
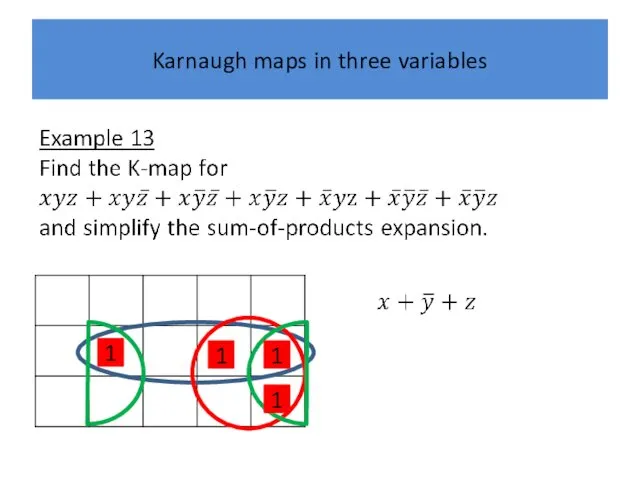
Karnaugh maps in three variables
1
1
1
1
Слайд 51
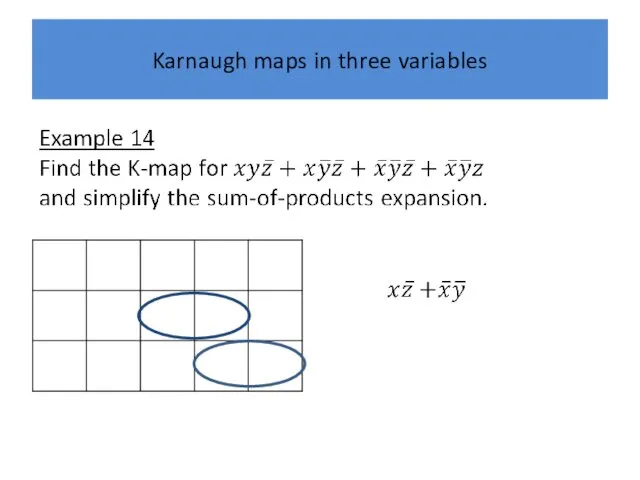
Karnaugh maps in three variables
Слайд 52
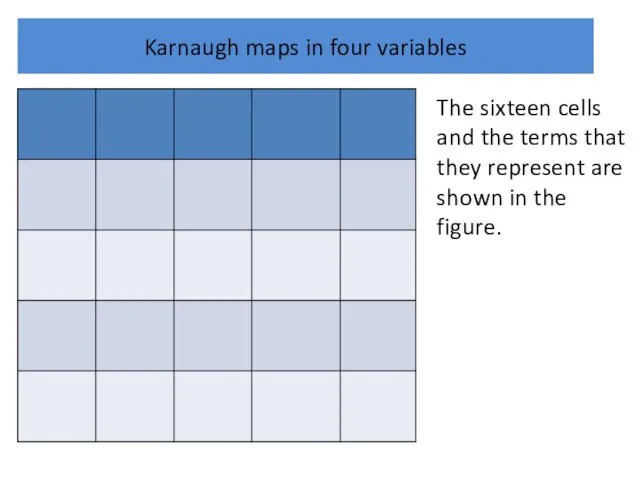
Karnaugh maps in four variables
The sixteen cells and the terms that
they represent are shown in the figure.
Слайд 53
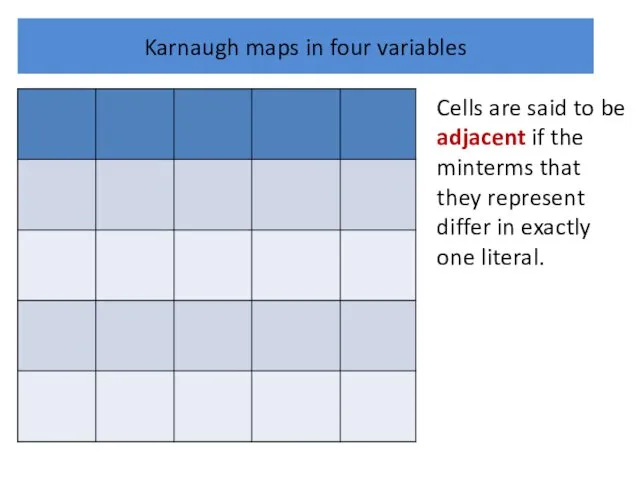
Karnaugh maps in four variables
Cells are said to be adjacent if
the minterms that they represent differ in exactly one literal.
Слайд 54
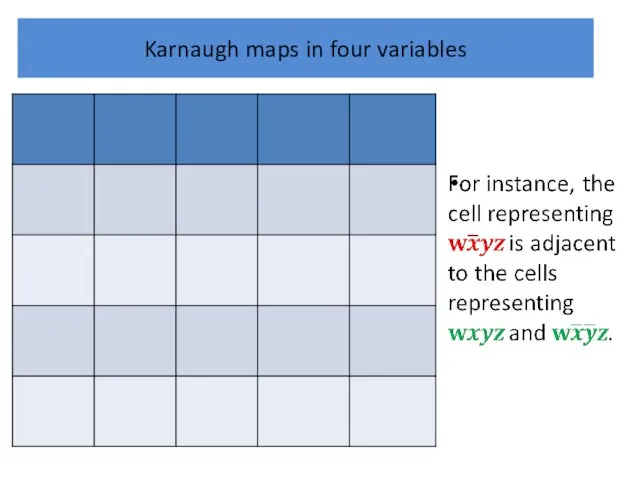
Karnaugh maps in four variables
Слайд 55

Karnaugh maps in four variables
The K-map of a sum-of-products expansion in
four variables can be thought of as lying on a torus, so that adjacent cells have a common boundary.
Слайд 56

Karnaugh maps in four variables
Слайд 57

Karnaugh maps in four variables
Слайд 58

Слайд 59

Слайд 60

Слайд 61

Слайд 62
Example 19 Simplify the sum-of-products expansion
Слайд 63
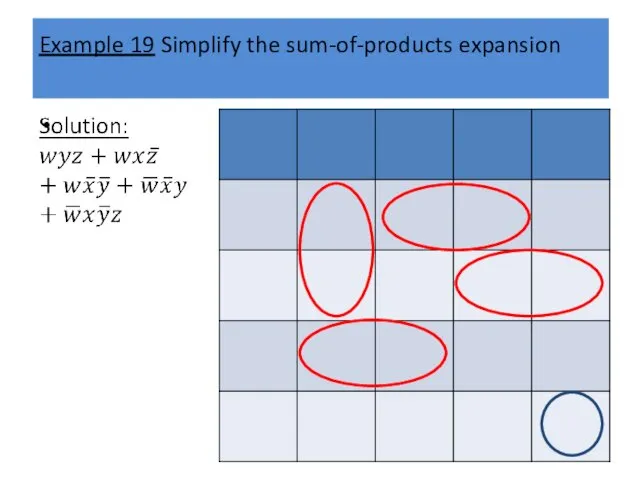
Example 19 Simplify the sum-of-products expansion
Слайд 64
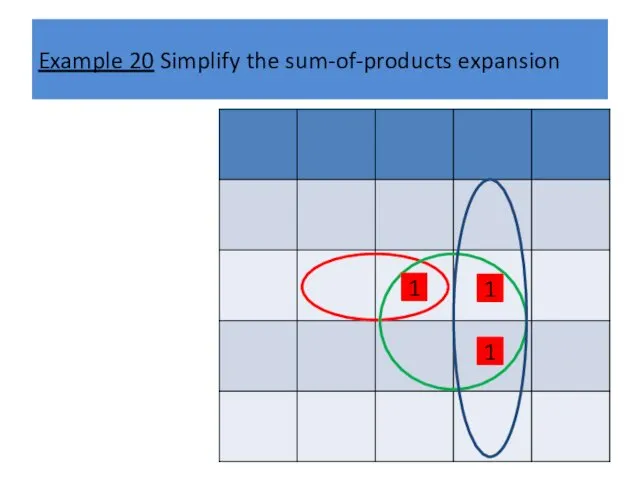
Example 20 Simplify the sum-of-products expansion
1
1
1
Слайд 65
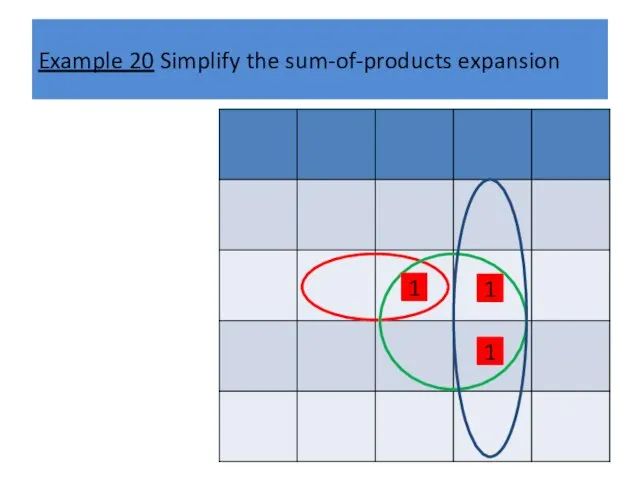
Example 20 Simplify the sum-of-products expansion
1
1
1
Слайд 66
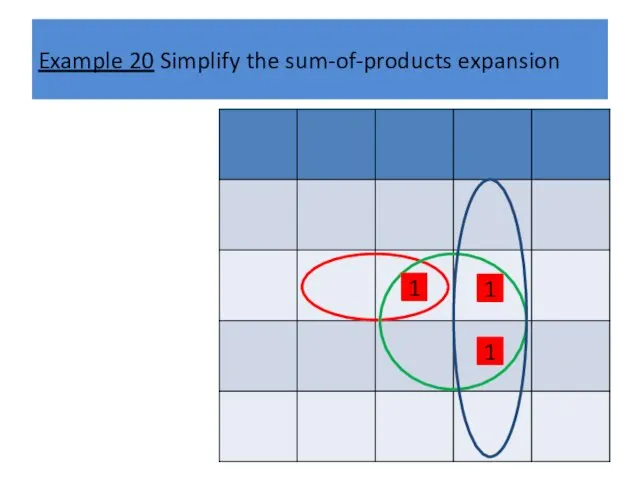
Example 20 Simplify the sum-of-products expansion
1
1
1
Слайд 67
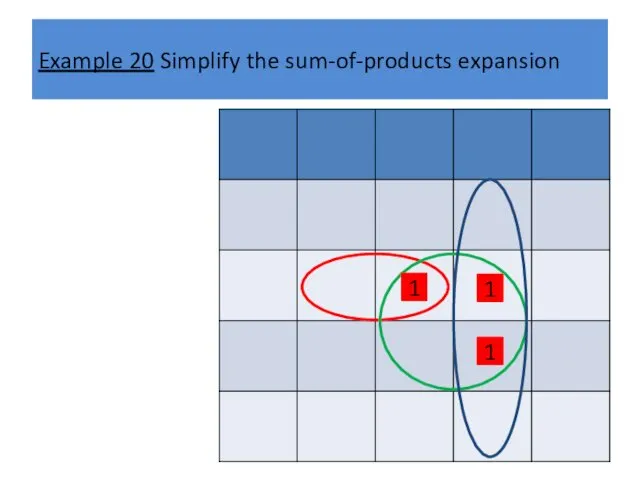
Example 20 Simplify the sum-of-products expansion
1
1
1
Слайд 68
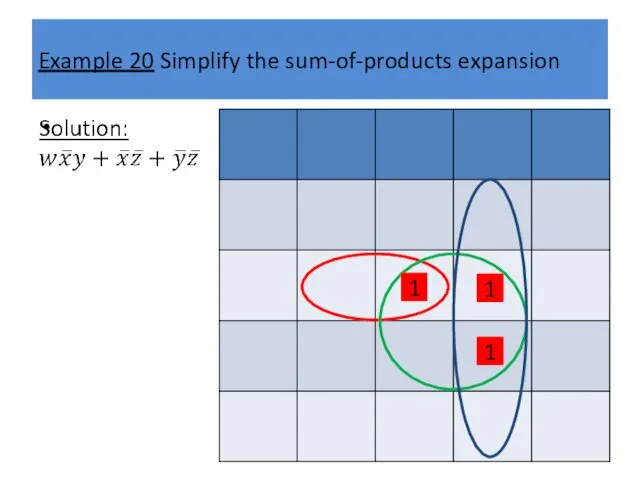
Example 20 Simplify the sum-of-products expansion
1
1
1
Слайд 69
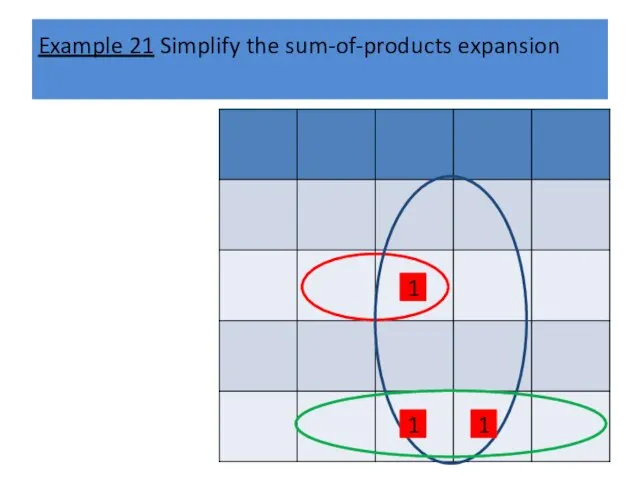
Example 21 Simplify the sum-of-products expansion
1
1
1
Слайд 70
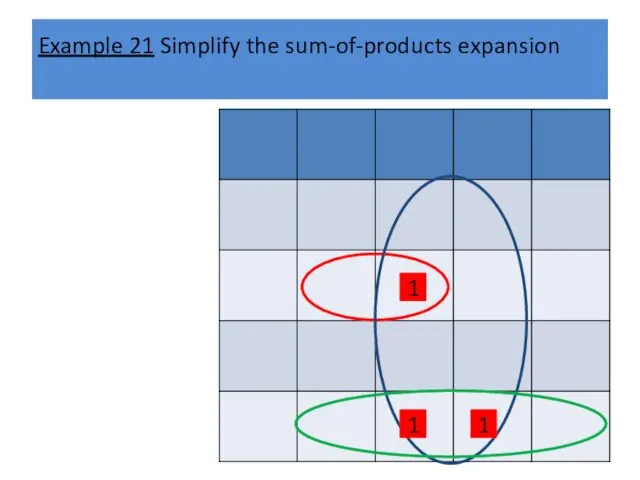
Example 21 Simplify the sum-of-products expansion
1
1
1
Слайд 71
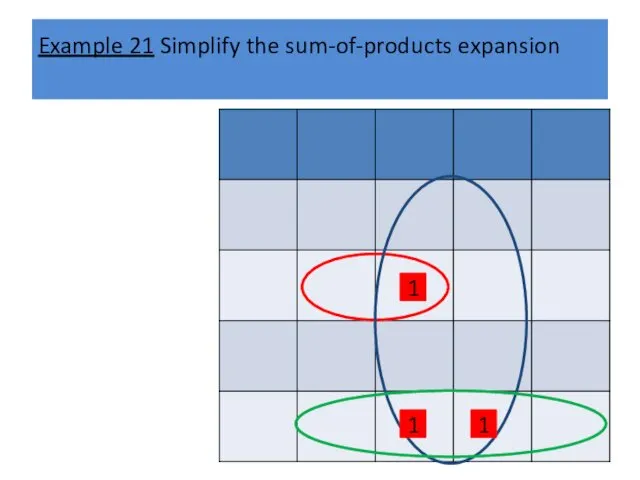
Example 21 Simplify the sum-of-products expansion
1
1
1
Слайд 72
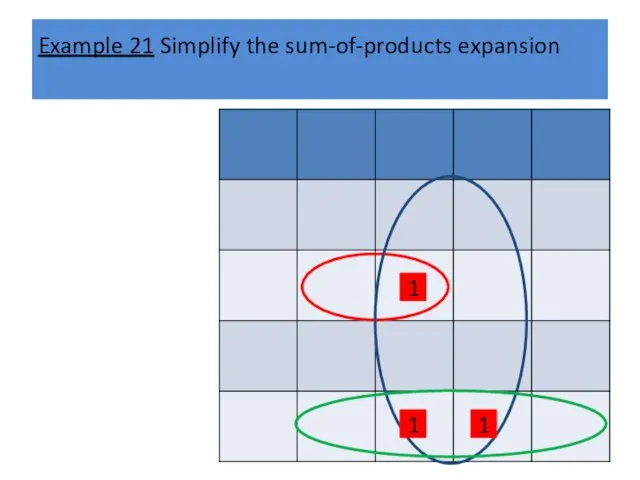
Example 21 Simplify the sum-of-products expansion
1
1
1
Слайд 73
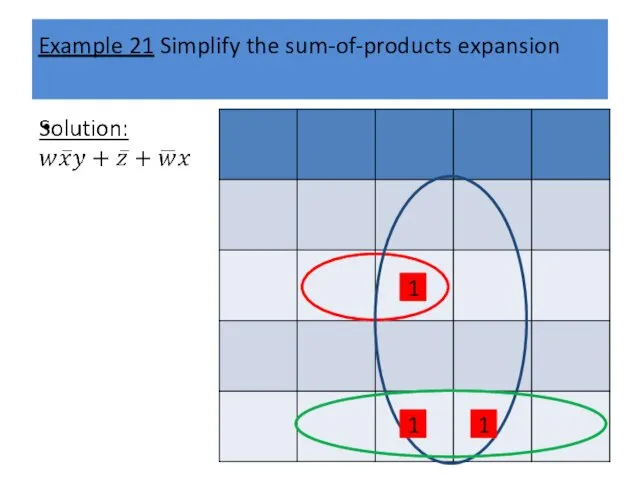
Example 21 Simplify the sum-of-products expansion
1
1
1
Слайд 74

Слайд 75

Circuits
The basic elements of circuits are called gates.
Each type of
gate implements a Boolean operation.
We define several types of gates. Using these gates, we will apply the rules of Boolean algebra to design circuits that perform a variety of tasks.
The circuits that we will study give output that depends only on the input, and not on the current state of the circuit. In other words, these circuits have no memory capabilities.
Such circuits are called combinational circuits or gating networks.
Слайд 76
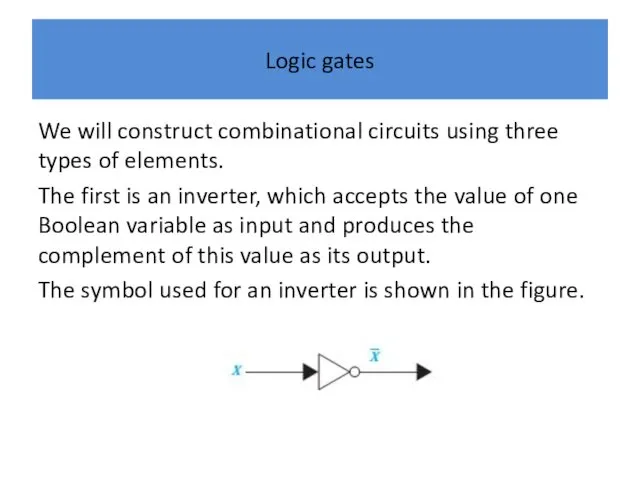
Logic gates
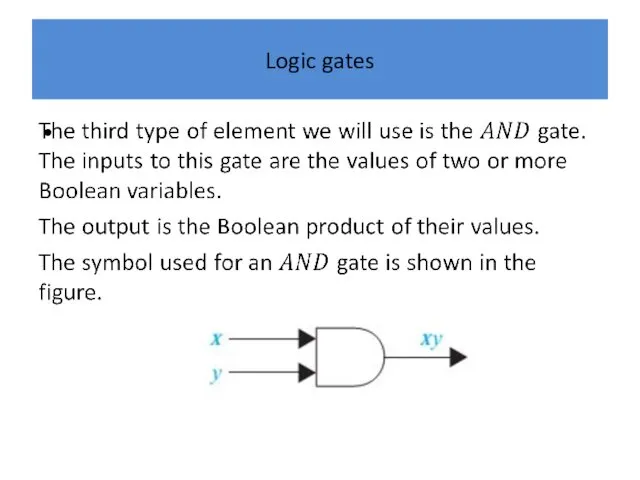
We will construct combinational circuits using three types of elements.
The first is an inverter, which accepts the value of one Boolean variable as input and produces the complement of this value as its output.
The symbol used for an inverter is shown in the figure.
Слайд 77
Слайд 78
Слайд 79

Слайд 80

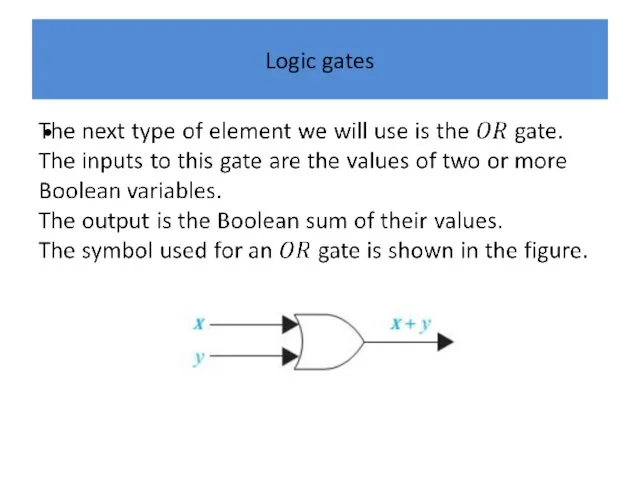
Circuits
The efficiency of a combinational circuit depends on the number and
arrangement of its gates.
The process of designing a combinational circuit begins with the table specifying the output for each combination of input values.
We can always use the sum-of-products expansion of a circuit to find a set of logic gates that will implement this circuit.
Слайд 81

Слайд 82
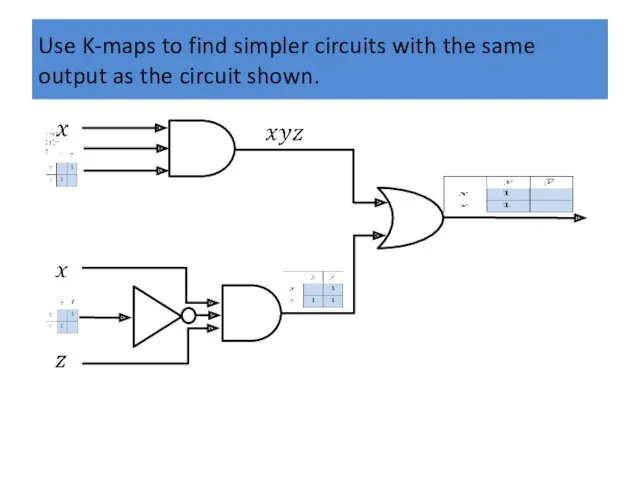
Use K-maps to find simpler circuits with the same output as
Слайд 83
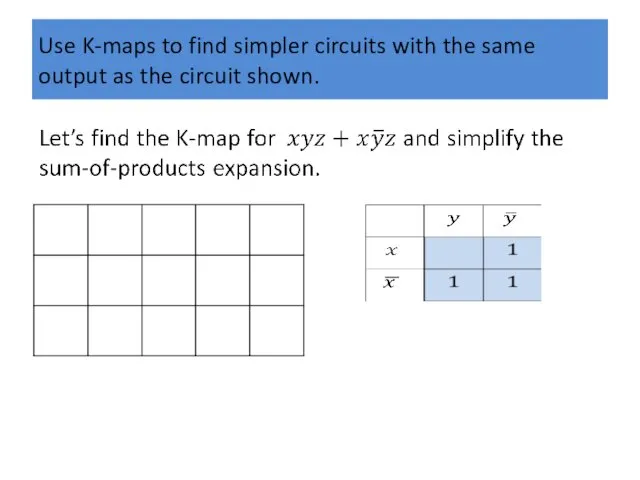
Use K-maps to find simpler circuits with the same output as


















































































 Творческое задание интернет-проекта Путешествие в мир химии
Творческое задание интернет-проекта Путешествие в мир химии Предмет, функции и объект исследования социологии
Предмет, функции и объект исследования социологии Система понятий дисциплины Литературное образование дошкольников
Система понятий дисциплины Литературное образование дошкольников Построение циклограммы. Основы поточной организации работ
Построение циклограммы. Основы поточной организации работ Разработка родительского собрания Наши дети не для насилия
Разработка родительского собрания Наши дети не для насилия Учет кассовых операций
Учет кассовых операций Процесс пищеварения в ротовой полости
Процесс пищеварения в ротовой полости Родительское собрание в подготовительной группе
Родительское собрание в подготовительной группе Проект Уберечь от дурмана
Проект Уберечь от дурмана Перша медична допомога
Перша медична допомога Игры на развитие мышления
Игры на развитие мышления Конвейер проектов – муниципальный конкурс проектов
Конвейер проектов – муниципальный конкурс проектов Спутниковые системы навигации. Угломерные бортовые РНС. Дальномерные РНС и радиовысотомеры
Спутниковые системы навигации. Угломерные бортовые РНС. Дальномерные РНС и радиовысотомеры Строение прокариотичекой клетки Айниятуллин Р.прБ-119
Строение прокариотичекой клетки Айниятуллин Р.прБ-119 Поздравление мамам
Поздравление мамам презентация к мероприятию 9 мая
презентация к мероприятию 9 мая Обогащение полезных ископаемых. Лекция 1-2
Обогащение полезных ископаемых. Лекция 1-2 Презентация День Победы.
Презентация День Победы. Republica de Cuba Cienfuegos y Santiago de Cuba
Republica de Cuba Cienfuegos y Santiago de Cuba Технологическая карта к занятию по теме Первые шаги в космос (Изготовление плоскостной ракеты со щелевидным соединением).
Технологическая карта к занятию по теме Первые шаги в космос (Изготовление плоскостной ракеты со щелевидным соединением). Ұлттық діндер
Ұлттық діндер Строение и работа сердца
Строение и работа сердца презентация по внеурочной деятельности
презентация по внеурочной деятельности Метод проблемного обучения
Метод проблемного обучения Исследовательская работа ученика 1 Б класса Хлапонина Захара Откуда у пчёл мёд?
Исследовательская работа ученика 1 Б класса Хлапонина Захара Откуда у пчёл мёд? Электрохимические технологии неорганических веществ
Электрохимические технологии неорганических веществ Определение соотношения составных частей и массы нетто консервов
Определение соотношения составных частей и массы нетто консервов Белки, жиры и углеводы
Белки, жиры и углеводы