Содержание
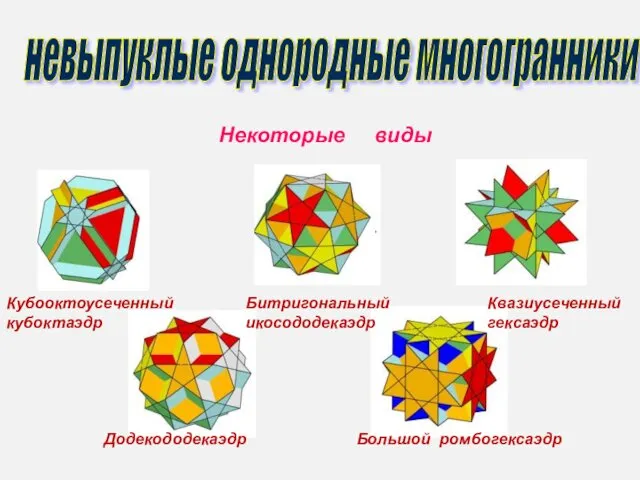
- 2. Кубооктоусеченный кубоктаэдр Битригональный икосододекаэдр Квазиусеченный гексаэдр Додекододекаэдр Большой ромбогексаэдр невыпуклые однородные многогранники Некоторые виды
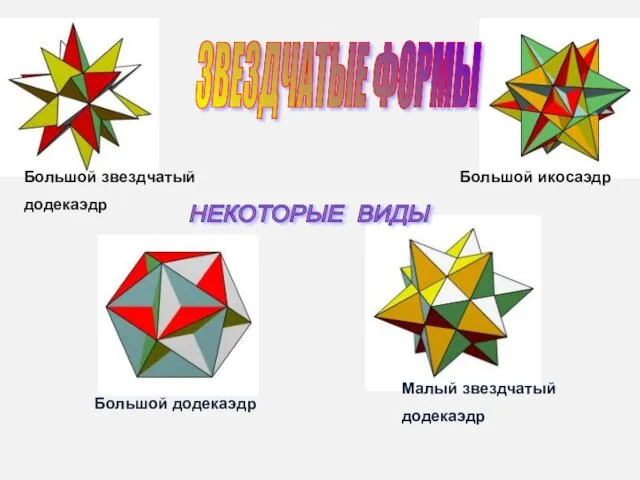
- 3. ЗВЕЗДЧАТЫЕ ФОРМЫ НЕКОТОРЫЕ ВИДЫ Малый звездчатый додекаэдр Большой додекаэдр Большой звездчатый додекаэдр Большой икосаэдр
- 4. Архимедовы тела Архимедовыми телами называются выпуклые многогранники , все многогранные углы которых равны, а грани правильные
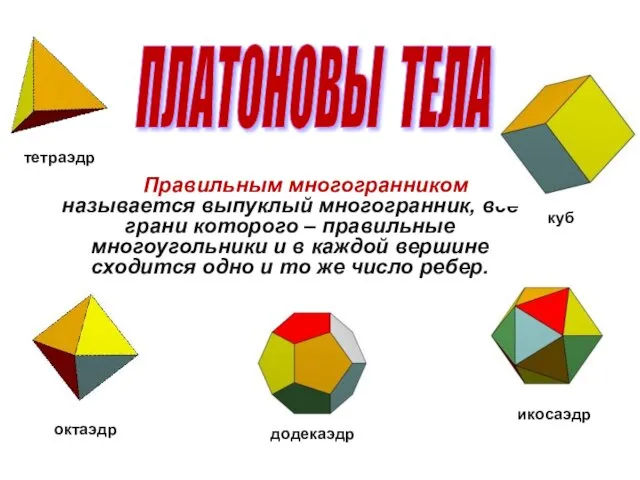
- 5. Правильным многогранником называется выпуклый многогранник, все грани которого – правильные многоугольники и в каждой вершине сходится
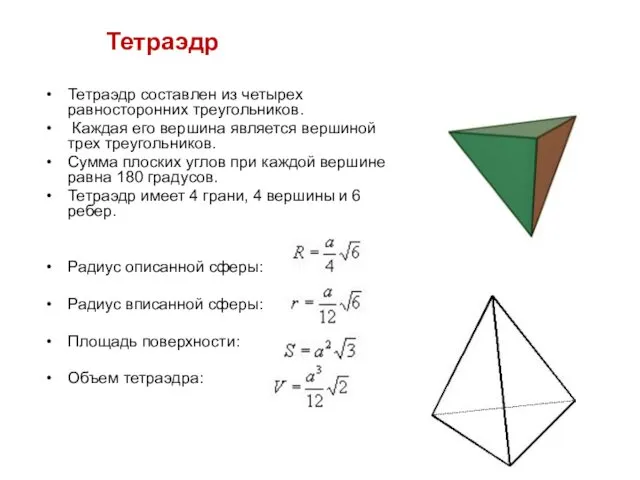
- 6. Тетраэдр
- 7. Куб (гексаэдр)
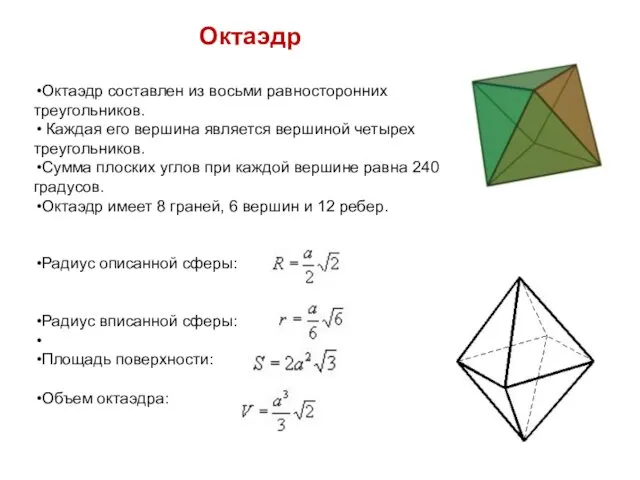
- 8. Октаэдр
- 9. Додекаэдр
- 10. Икосаэдр
- 11. Леонардо да Винчи любил делать из дерева каркасные модели многогранников. Когда его друг Пачоли издал в
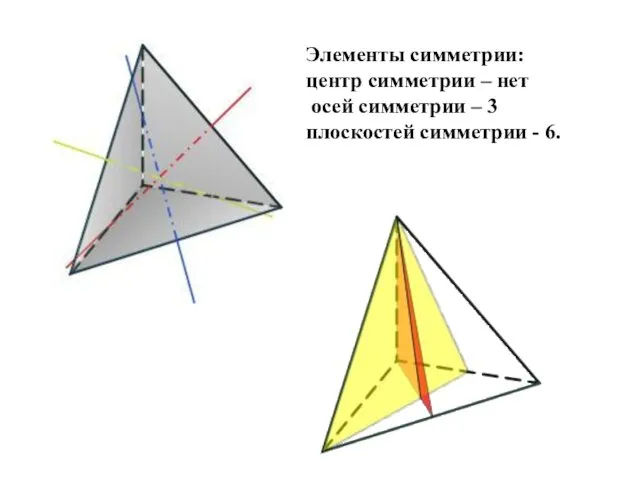
- 12. Тетраэдр Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских
- 13. Элементы симметрии: центр симметрии – нет осей симметрии – 3 плоскостей симметрии - 6.
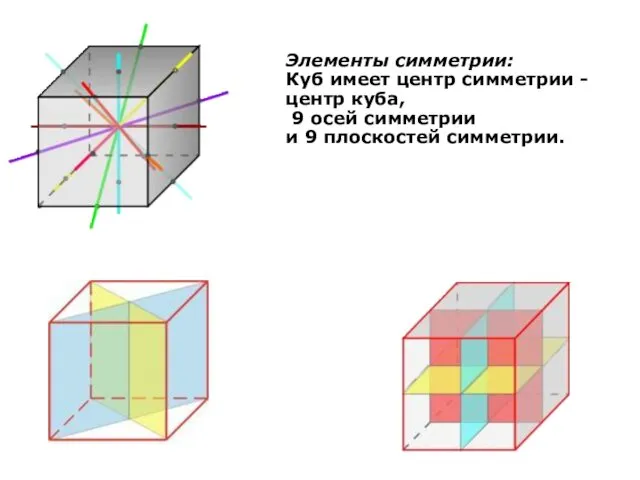
- 14. Куб (гексаэдр) Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских
- 15. Элементы симметрии: Куб имеет центр симметрии - центр куба, 9 осей симметрии и 9 плоскостей симметрии.
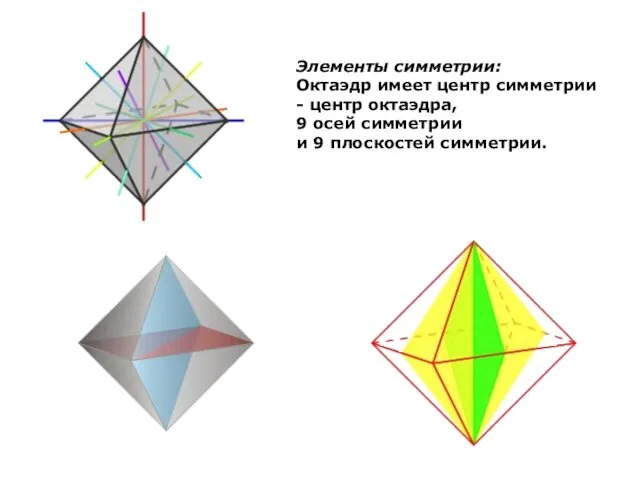
- 16. Октаэдр Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Сумма плоских
- 17. Элементы симметрии: Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
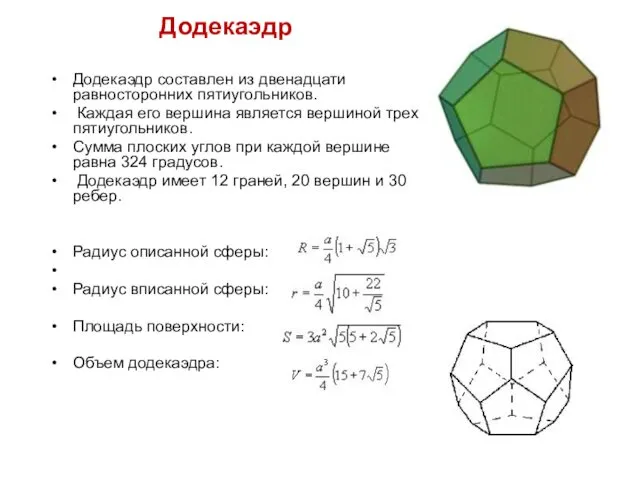
- 18. Додекаэдр Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских
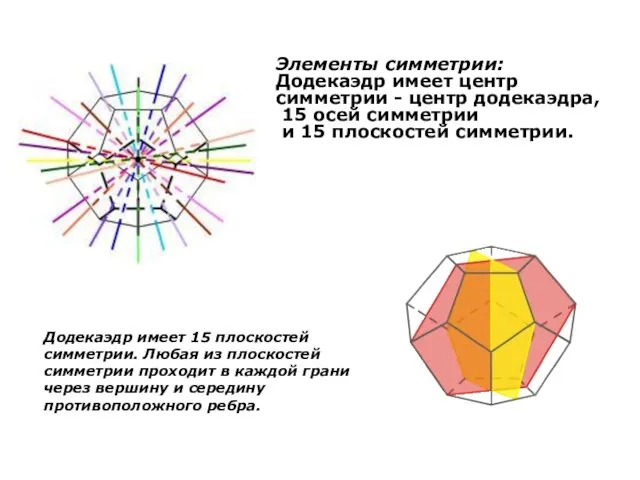
- 19. Элементы симметрии: Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.
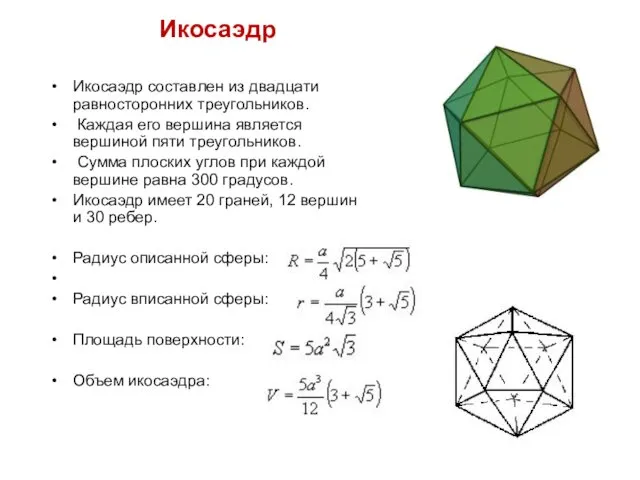
- 20. Икосаэдр Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских
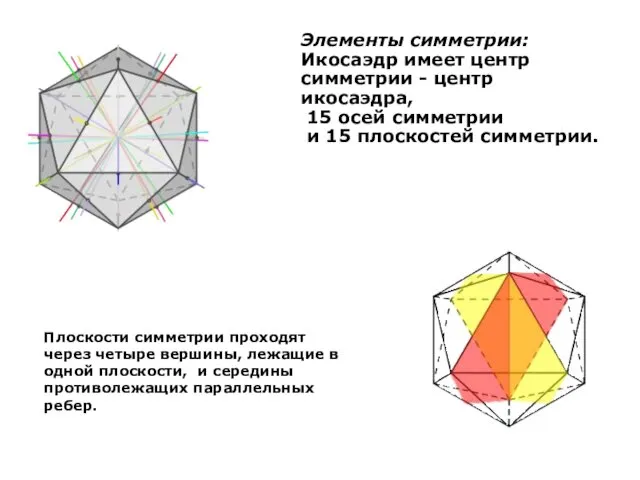
- 21. Элементы симметрии: Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.
- 22. Правильные многогранники существовали на Земле задолго до появления на ней человека- кубы поваренной соли, тетраэдры сурьмянистого
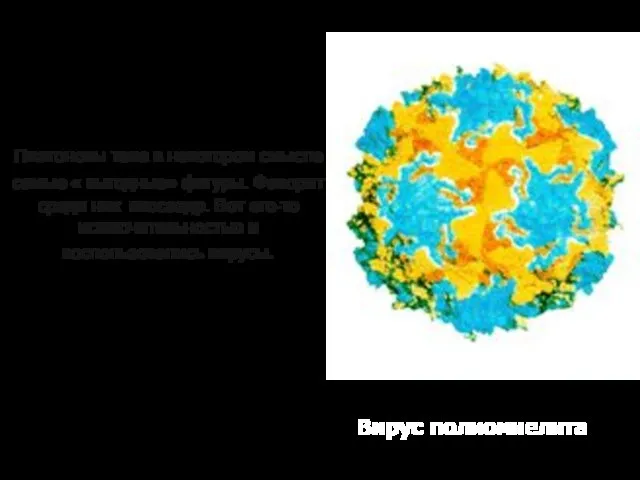
- 23. Платоновы тела в некотором смысле самые « выгодные» фигуры. Фаворит среди них икосаэдр. Вот его-то исключительностью
- 24. На гравюре "Четыре тела" (Эшер) изображено пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме
- 25. ДРУГОЙ МИР
- 26. Если вы услышите, что кто-то не любит математику, не верьте. Её нельзя не любить- она и
- 28. Скачать презентацию












 MDI tech. Комплекс услуг по проектированию и мелкосерийному производству различных видов продукции
MDI tech. Комплекс услуг по проектированию и мелкосерийному производству различных видов продукции Сосудисто-тромбоцитарное звено системы гемостаза
Сосудисто-тромбоцитарное звено системы гемостаза Проектирование отделения асбестообогатительной фабрики для ведения технологического процесса
Проектирование отделения асбестообогатительной фабрики для ведения технологического процесса Народные восстания в эпоху Петра I
Народные восстания в эпоху Петра I Тип плоские черви
Тип плоские черви Десять основных положений нового закона Об образовании в РФ
Десять основных положений нового закона Об образовании в РФ Триединое единство. Презентация по курсу Брак и семья
Триединое единство. Презентация по курсу Брак и семья Строительство жилого трехэтажного кирпичного дома
Строительство жилого трехэтажного кирпичного дома химические свойства бензола
химические свойства бензола История болезни
История болезни Районный экологический фотоконкурс Мой родной Каширский край зимой
Районный экологический фотоконкурс Мой родной Каширский край зимой Обработка спинки женского пальто
Обработка спинки женского пальто Разработка технологических процессов и проектирование изделий
Разработка технологических процессов и проектирование изделий ФГТ В ДОУ
ФГТ В ДОУ Скелет человека
Скелет человека 20231008_maslenitsa1
20231008_maslenitsa1 Классный уголок
Классный уголок Водный орех (чилим)
Водный орех (чилим) Тепломассообмен в биосфере. Введение, некоторые математические понятия
Тепломассообмен в биосфере. Введение, некоторые математические понятия Реализация приоритетного проекта Формирование комфортной городской среды на территории МО Заостровское на 2018 год
Реализация приоритетного проекта Формирование комфортной городской среды на территории МО Заостровское на 2018 год Настольные игры
Настольные игры konflikt_prezentatsiya
konflikt_prezentatsiya Авиакомпания Аэрофлот
Авиакомпания Аэрофлот Я - воспитатель
Я - воспитатель Назначение разъездов и их классификация
Назначение разъездов и их классификация Викторина
Викторина Система отношений власти и бизнеса. (Лекция 2)
Система отношений власти и бизнеса. (Лекция 2) Акция 7+1 Петровская Слобода
Акция 7+1 Петровская Слобода