Содержание
- 2. Сигналы Периодические – непериодические Непрерывные - дискретные
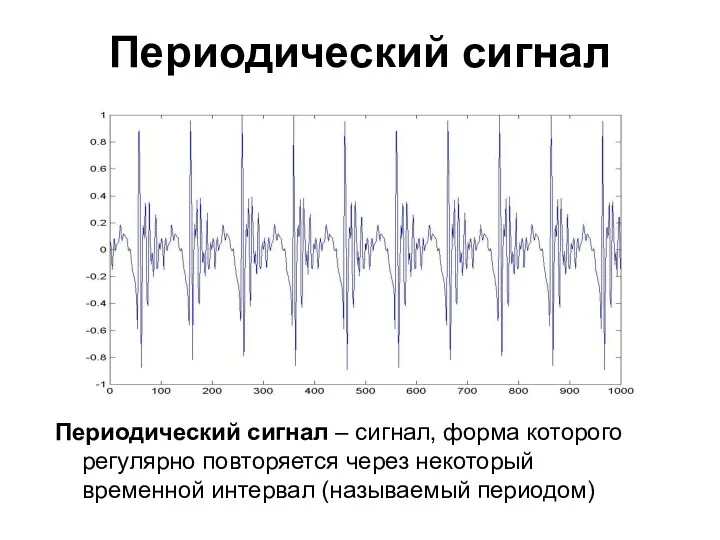
- 3. Периодический сигнал Периодический сигнал – сигнал, форма которого регулярно повторяется через некоторый временной интервал (называемый периодом)
- 4. Математическое определение Сигнал x(t) называется периодическим с периодом Т, если x(t + T) = x(t) для
- 5. Свойства Если Т – период колебания, то 2T, 3T, 4T, …, а также -T, -2T, -3T,
- 6. Вывод Строго говоря, периодическое колебание – абстракция, которой в реальности нет (хотя бы потому, что в
- 7. Частота Если Т – период колебания, то частотой колебания называется величина F = 1/T Частота измеряется
- 8. Круговая частота Если F – частота колебания, то круговой частотой того же колебания называют ω =
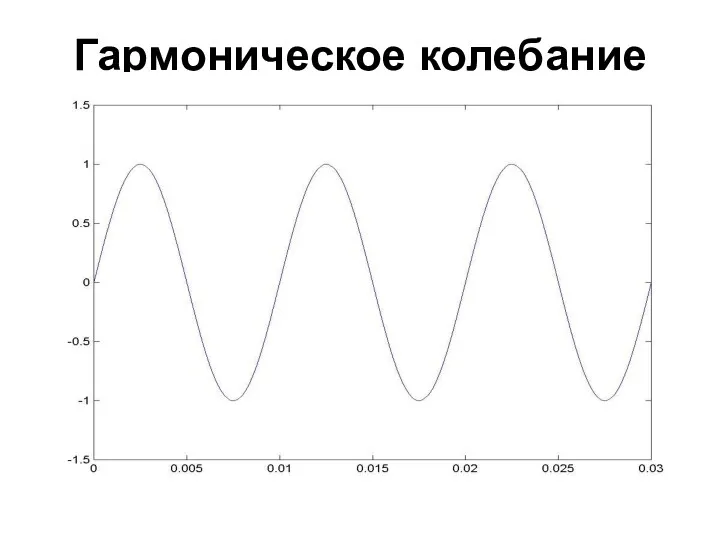
- 9. Гармоническое колебание
- 10. Физические примеры гармонических колебаний Маятник Грузик на пружинке
- 11. Общая запись x(t) = A*sin(2*π*F + ϕ) A – амплитуда гармонического колебания F – частота гармонического
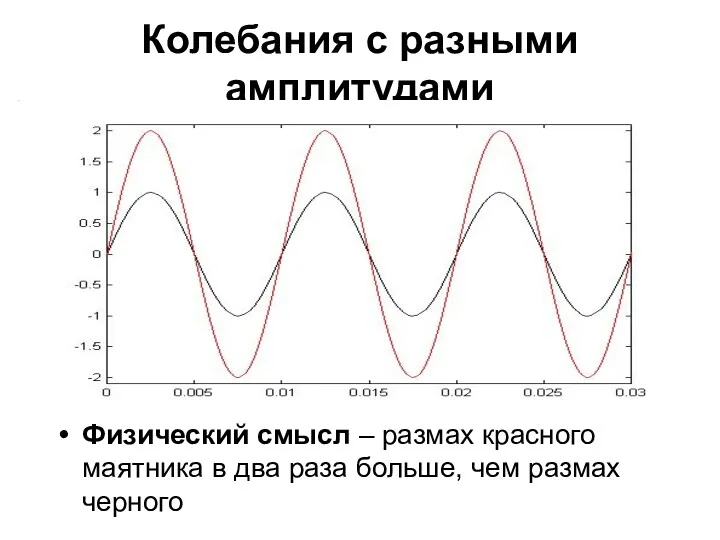
- 12. Колебания с разными амплитудами Физический смысл – размах красного маятника в два раза больше, чем размах
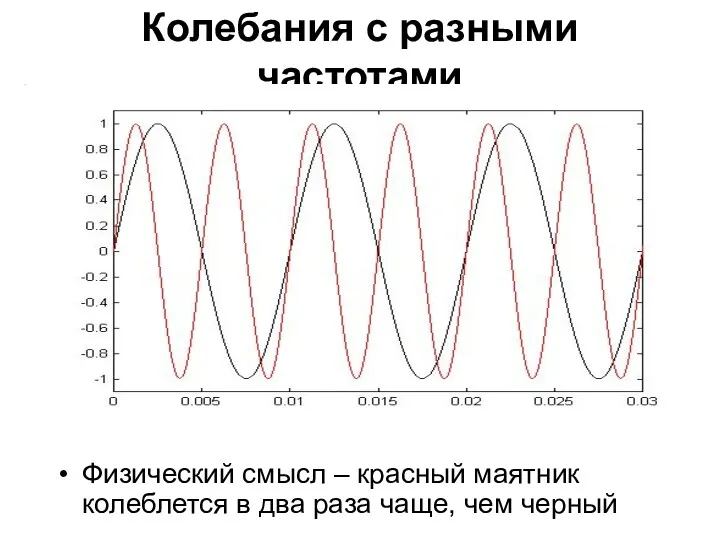
- 13. Колебания с разными частотами Физический смысл – красный маятник колеблется в два раза чаще, чем черный
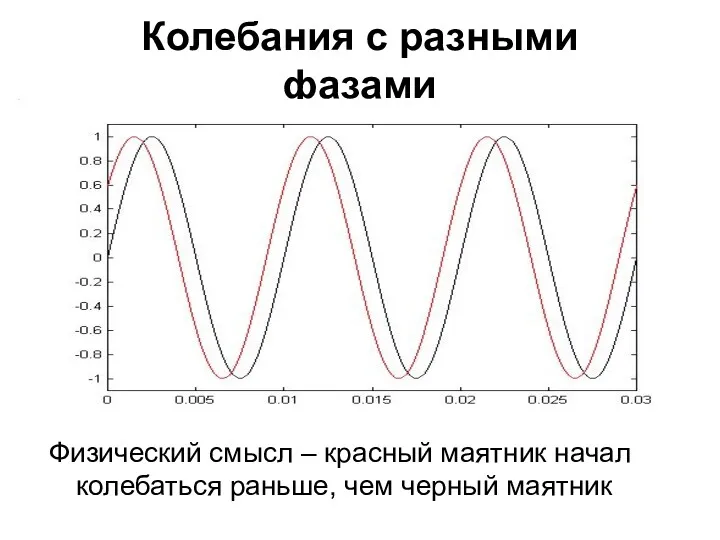
- 14. Колебания с разными фазами Физический смысл – красный маятник начал колебаться раньше, чем черный маятник
- 15. Можно собирать периодические колебания, суммируя гармонические с разными частотами, амплитудами и фазами
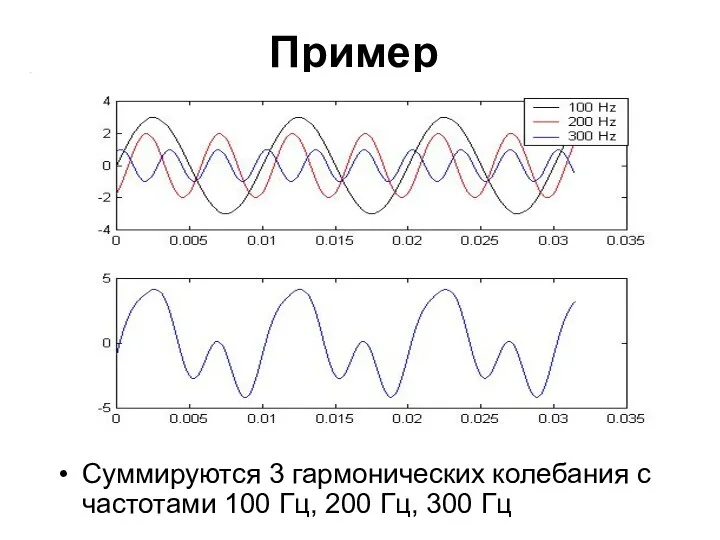
- 16. Пример Суммируются 3 гармонических колебания с частотами 100 Гц, 200 Гц, 300 Гц
- 17. Функция sum_3harmonics – суммирует и рисует 3 гармоники с частотами 100 Гц, 200 Гц, 300 Гц
- 18. Пример sum_3harmonics([3,2,1],[0,0,0])
- 19. Можно ли произвольное периодическое колебание разложить на сумму гармонических?
- 20. Теорема Фурье Всякое периодическое колебание частоты F можно получить в результате суммирования бесконечного числа гармоник с
- 21. Терминология Гармоника с частотой F называется основной гармоникой Гармоники с частотами 2F, 3F, 4F, …, называются
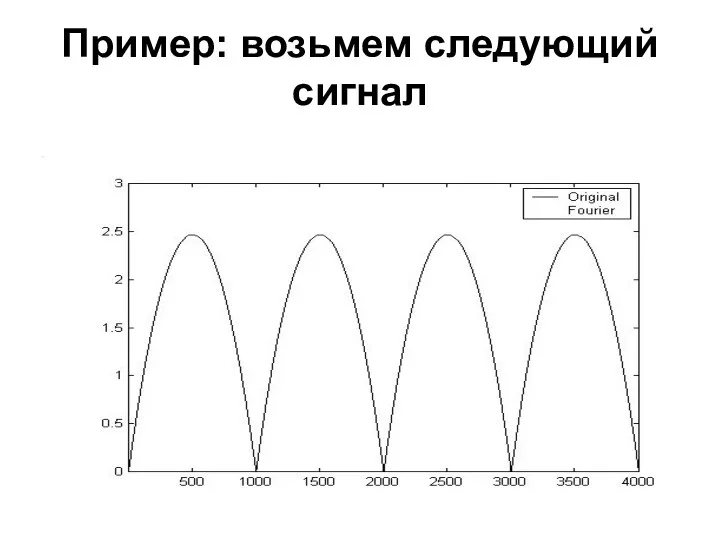
- 22. Пример: возьмем следующий сигнал
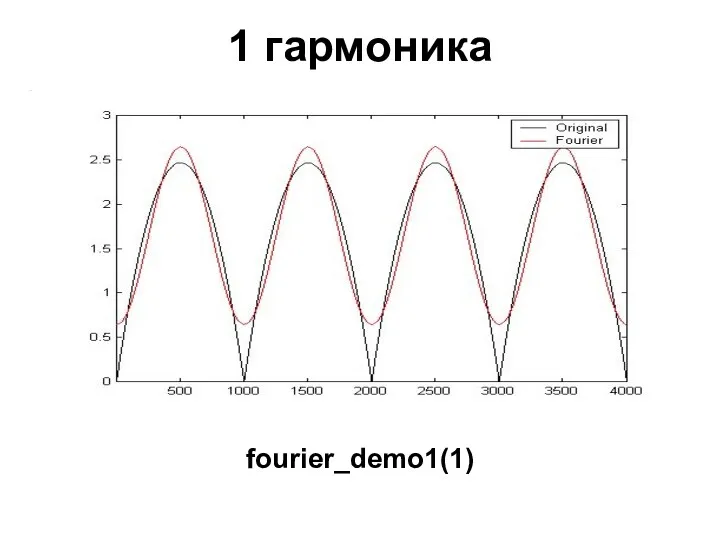
- 23. 1 гармоника fourier_demo1(1)
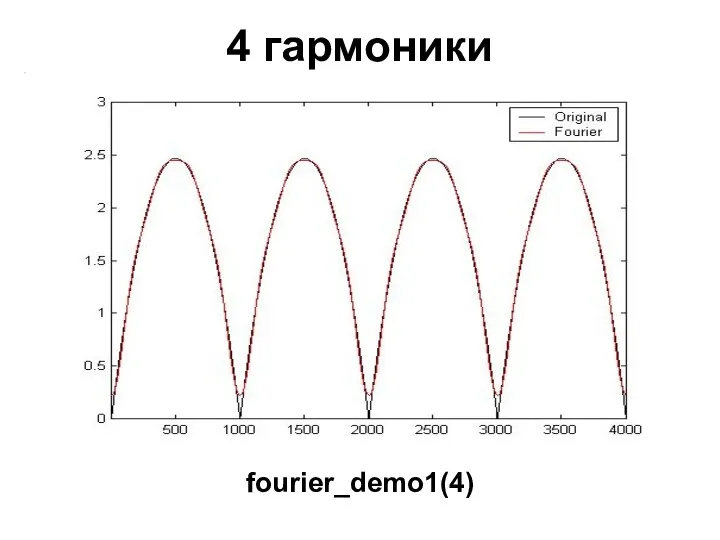
- 24. 4 гармоники fourier_demo1(4)
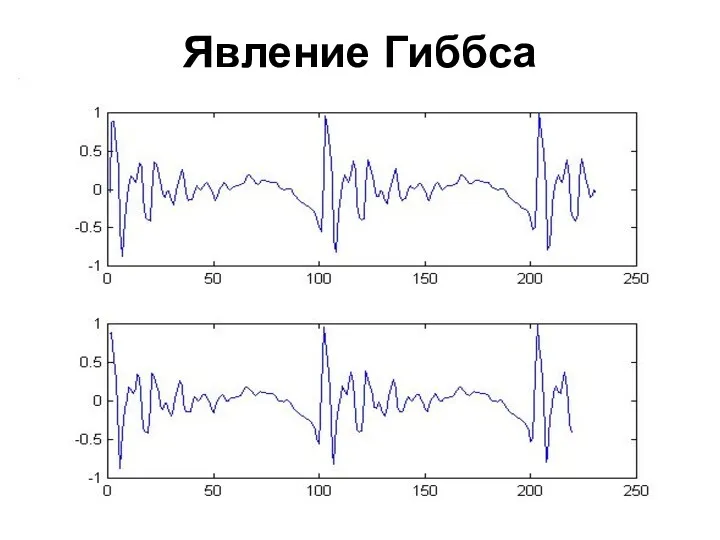
- 25. Явление Гиббса
- 26. Пример
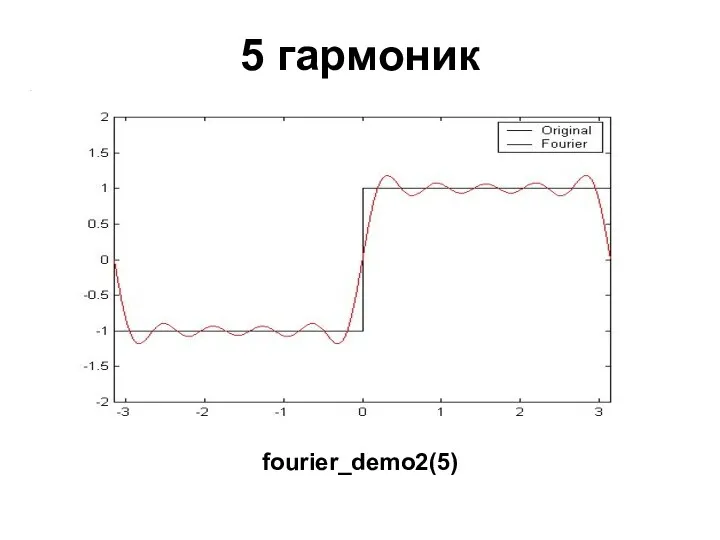
- 27. 5 гармоник fourier_demo2(5)
- 28. 20 гармоник fourier_demo2(20)
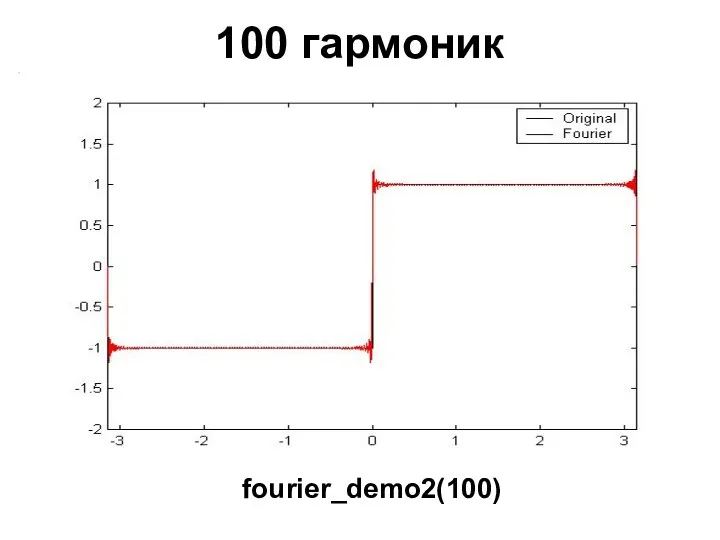
- 29. 100 гармоник fourier_demo2(100)
- 30. Явление Гиббса Явление Гиббса – появление пульсаций значительной амплитуды в окрестности скачкообразного изменения сигнала При этом
- 31. Явление Гиббса Таким образом, если в сигнале есть скачки, то в окрестности этих скачков разложение Фурье
- 32. В чем опасность явления Гиббса?
- 33. Явление Гиббса
- 34. Аналого-цифровое преобразование Передача голоса через цифровую сеть Для преобразования используется КОДЕК (кодер-декодер) Аналоговый сигнал Цифровой сигнал
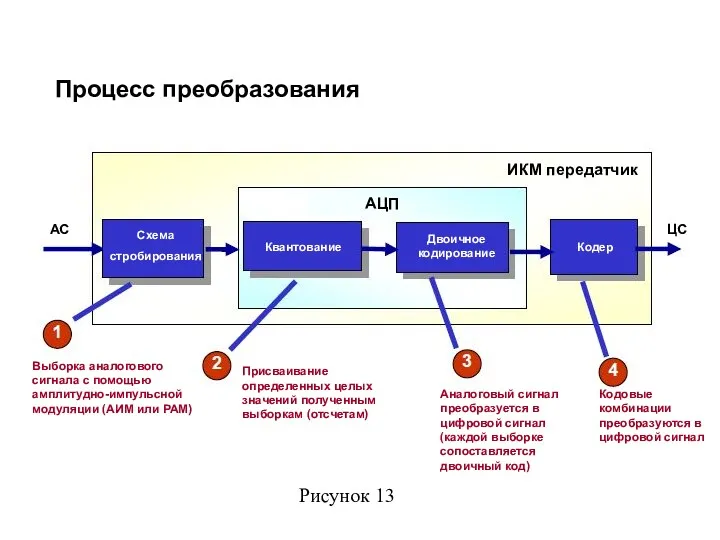
- 35. Процесс преобразования АС ИКМ передатчик АЦП ЦС Выборка аналогового сигнала с помощью амплитудно-импульсной модуляции (АИМ или
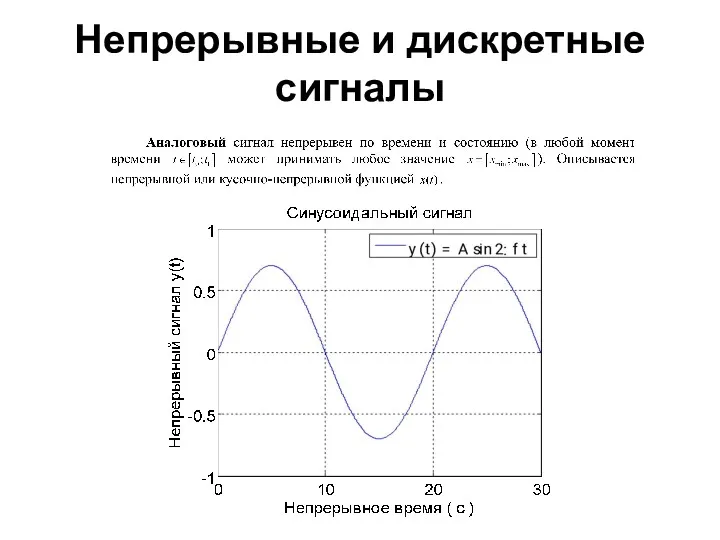
- 36. Непрерывные и дискретные сигналы
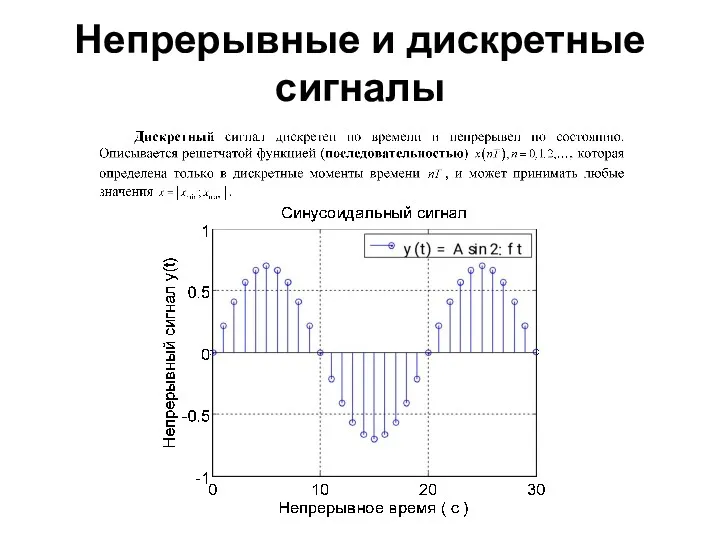
- 37. Непрерывные и дискретные сигналы
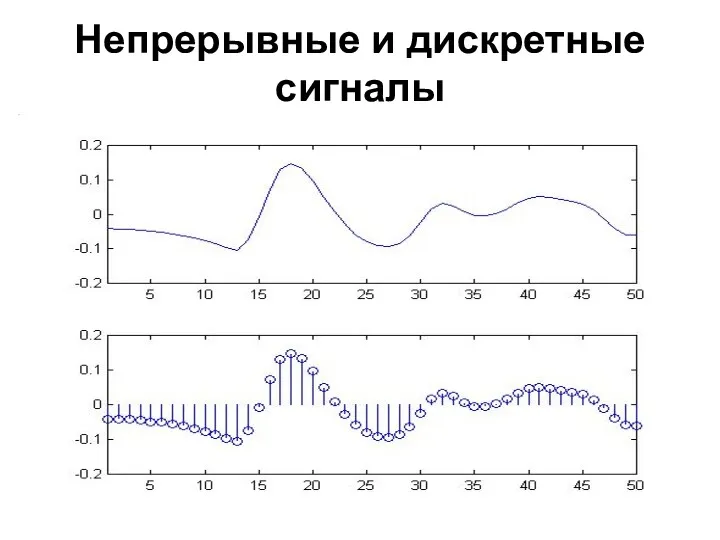
- 38. Непрерывные и дискретные сигналы
- 39. Дискретизация и квантование При вводе непрерывного сигнала в компьютер сигнал дискретизируется и квантуется Фонетист всегда имеет
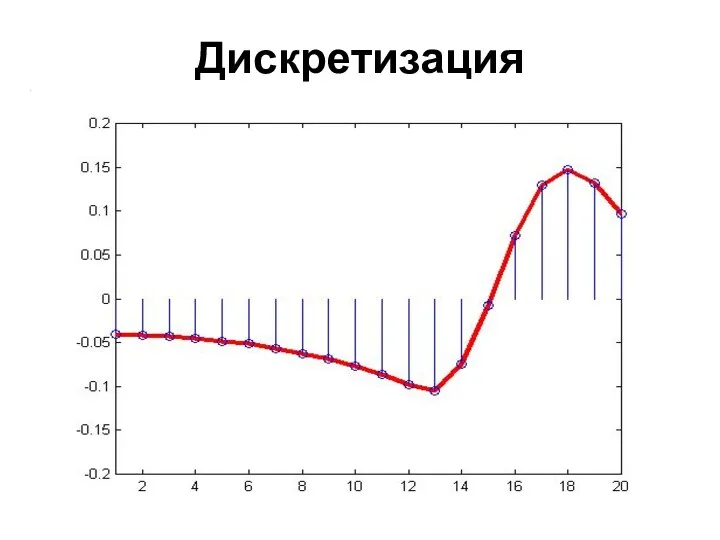
- 40. Дискретизация
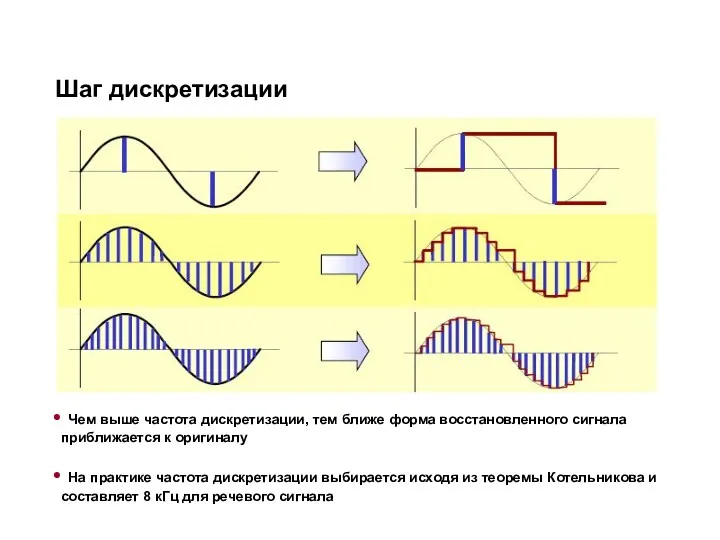
- 41. Шаг дискретизации Чем выше частота дискретизации, тем ближе форма восстановленного сигнала приближается к оригиналу На практике
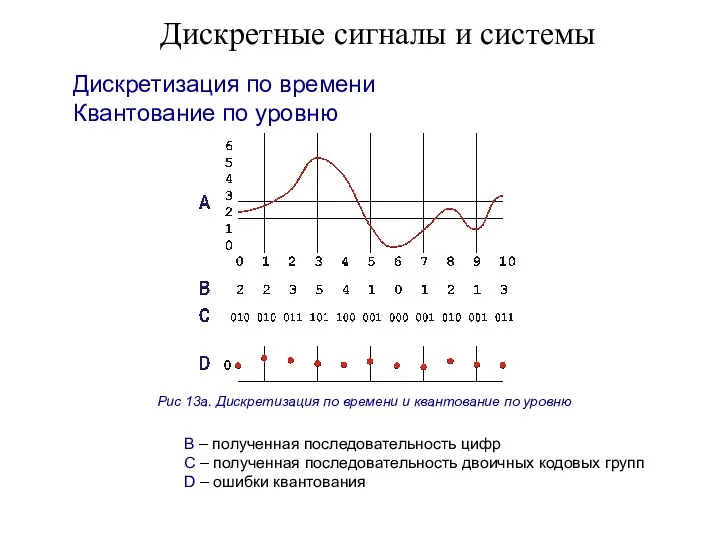
- 42. Дискретные сигналы и системы Дискретизация по времени Квантование по уровню Рис 13а. Дискретизация по времени и
- 43. Частота дискретизации
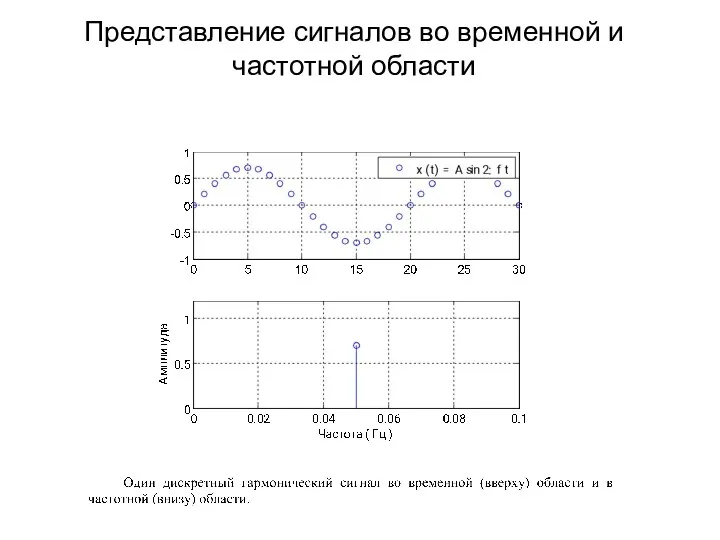
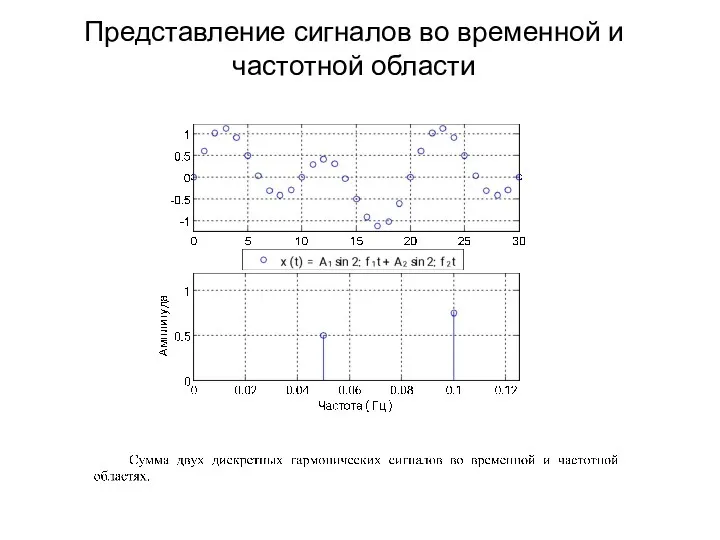
- 44. Представление сигналов во временной и частотной области
- 45. Представление сигналов во временной и частотной области
- 46. Частота дискретизации Интервал дискретизации (sampling period) Δt – интервал времени между двумя соседними временными отсчетами Частота
- 47. Пример Если частота дискретизации сигнала = 16 кГц, то это означает, что за 1 секунду запоминаются
- 48. Насколько часто нужно запоминать отсчеты непрерывного сигнала?
- 49. Теорема Котельникова Если спектр непрерывного сигнала не содержит информации выше частоты F, то частота дискретизации должна
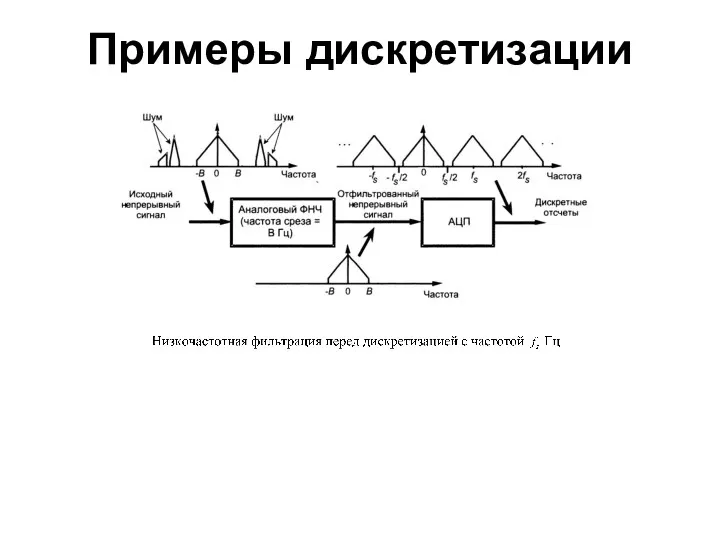
- 50. Применительно к речи Считается, что спектральные компоненты выше 3400 Гц не влияют на разборчивость речи Поэтому
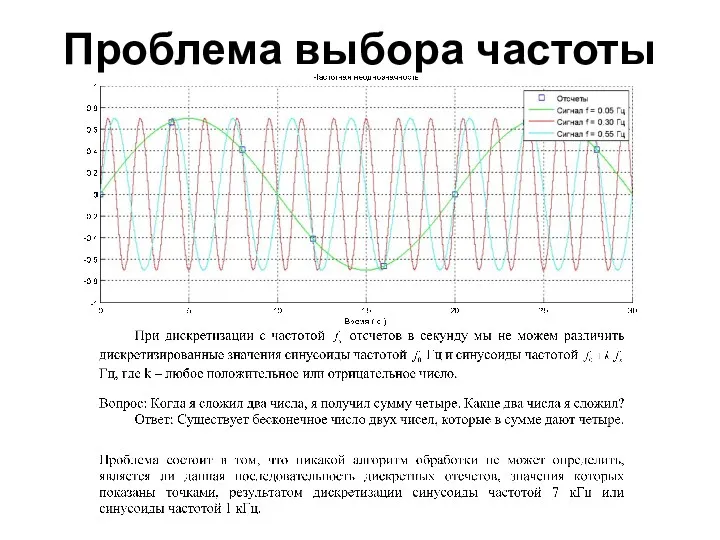
- 51. Проблема выбора частоты
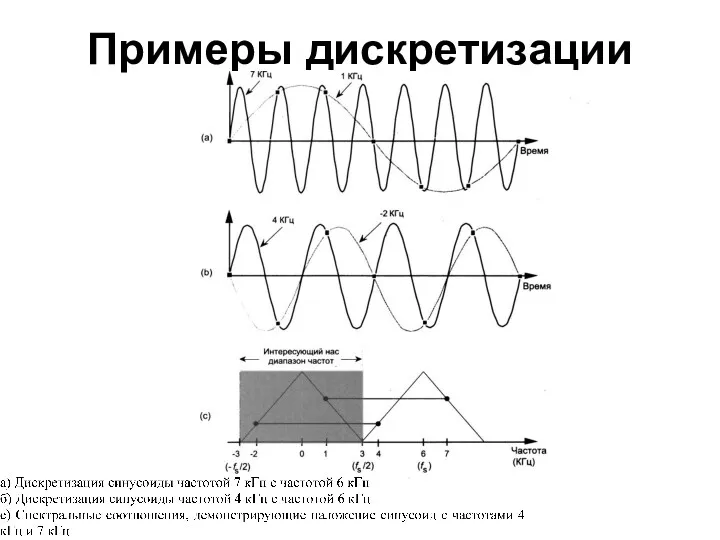
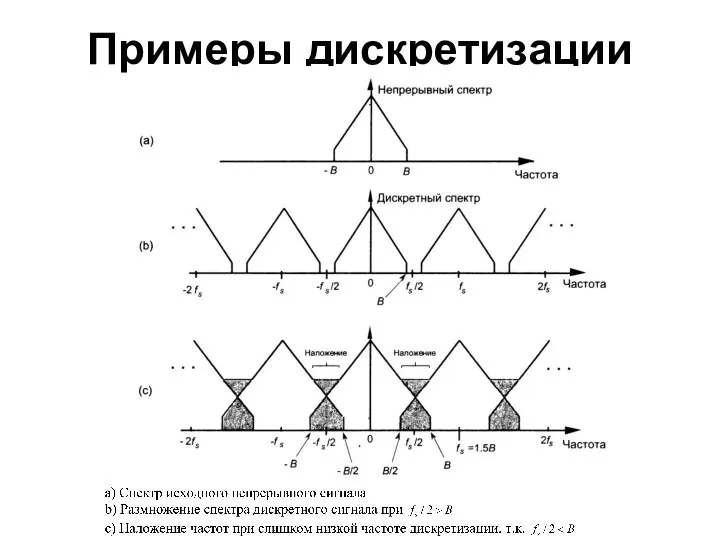
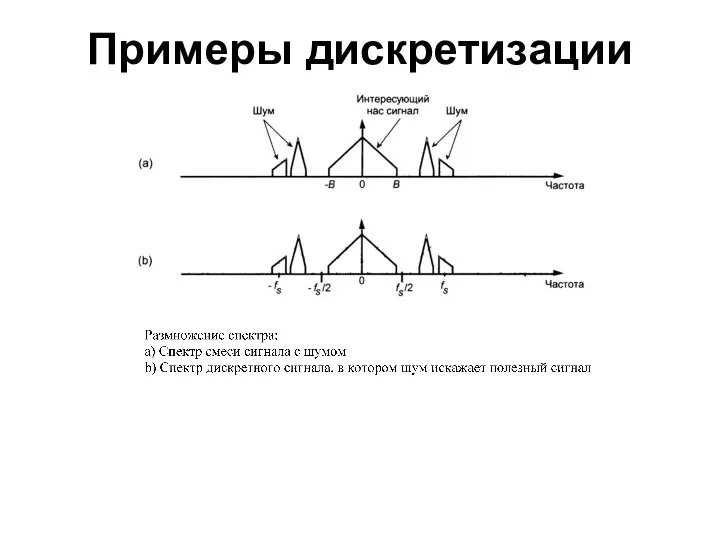
- 52. Примеры дискретизации
- 53. Примеры дискретизации
- 54. Примеры дискретизации
- 55. Примеры дискретизации
- 56. Примеры дискретизации
- 57. Примеры дискретизации
- 58. Ресэмплирование Ресэмплирование (resampling) – переход от одной частоты дискретизации к другой
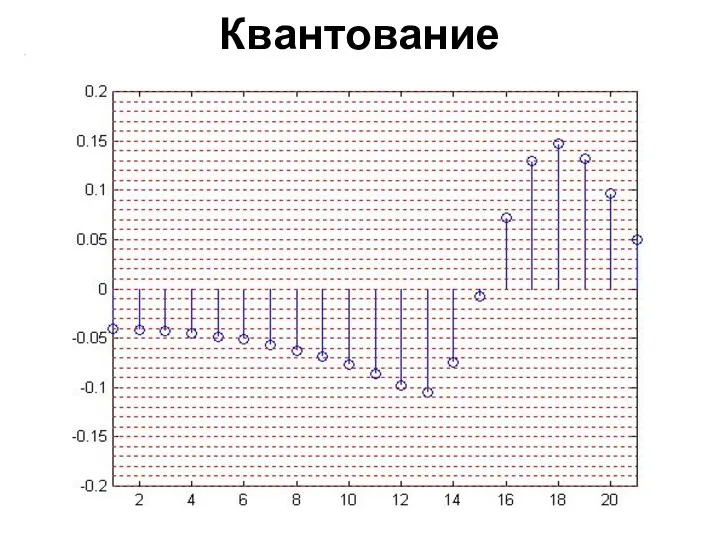
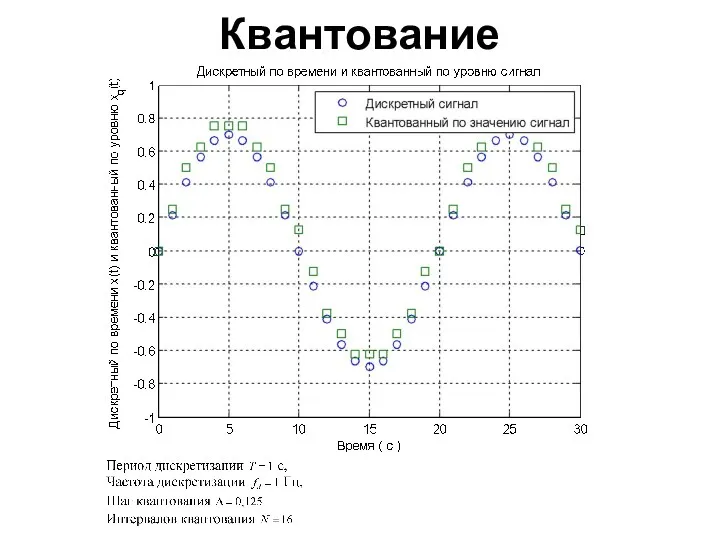
- 59. Квантование
- 60. Квантование
- 61. Квантование Исходно имеется дискретный набор возможных значений амплитуд (уровней квантования) Квантование сводится к тому, что значение
- 62. Квантование Чем больше уровней квантования, тем меньше ошибка, возникающая из-за округления (т.наз. шум квантования) Количество уровней
- 63. Пример Пусть используется квантование 16 бит / отсчет (16 бит на отсчет) Это означает, что общее
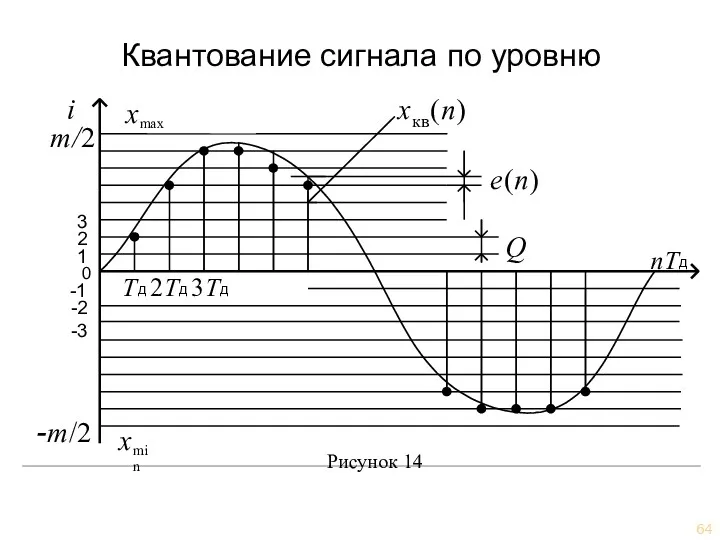
- 64. Погрешность квантования eкв(n) = хкв(n) − x(n) Квантование сигнала по уровню Рисунок 14
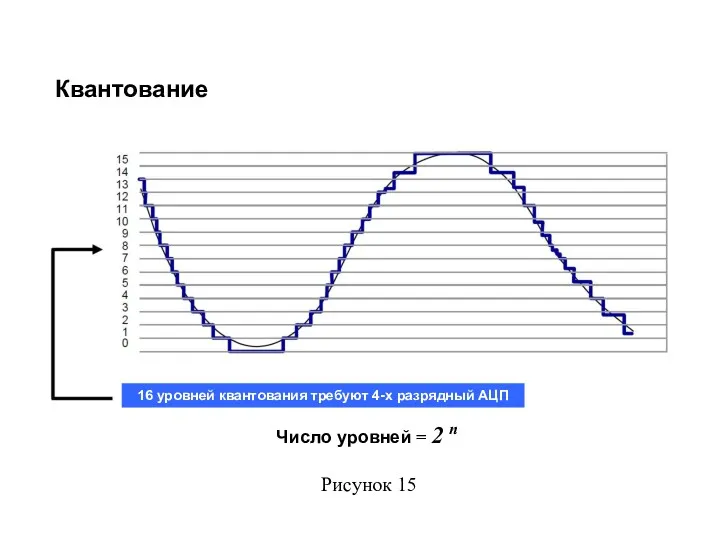
- 65. Квантование 16 уровней квантования требуют 4-х разрядный АЦП Число уровней = 2 n Рисунок 15
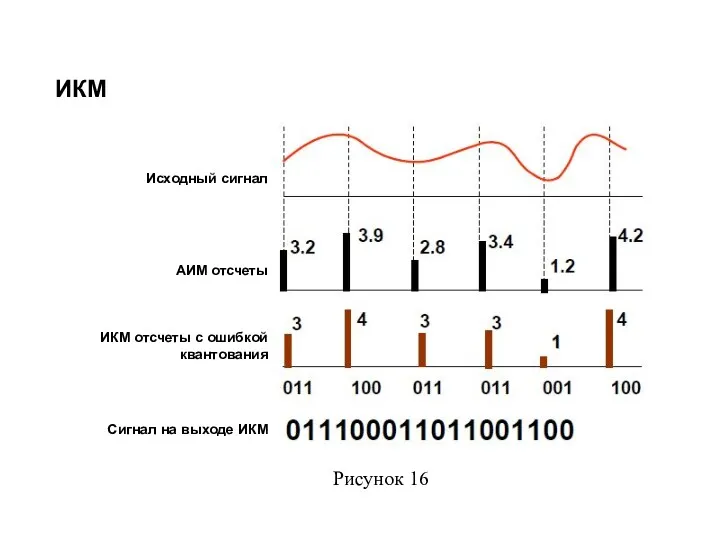
- 66. ИКМ Исходный сигнал АИМ отсчеты ИКМ отсчеты с ошибкой квантования Сигнал на выходе ИКМ Рисунок 16
- 67. Ошибки квантования Преобразование непрерывного по уровню сигнала в цифровой - это операция квантования (quantization). Термин "квантование"
- 68. Дискретные сигналы и системы Квантование по уровню Рис 17 - Получение двоичных кодовых групп
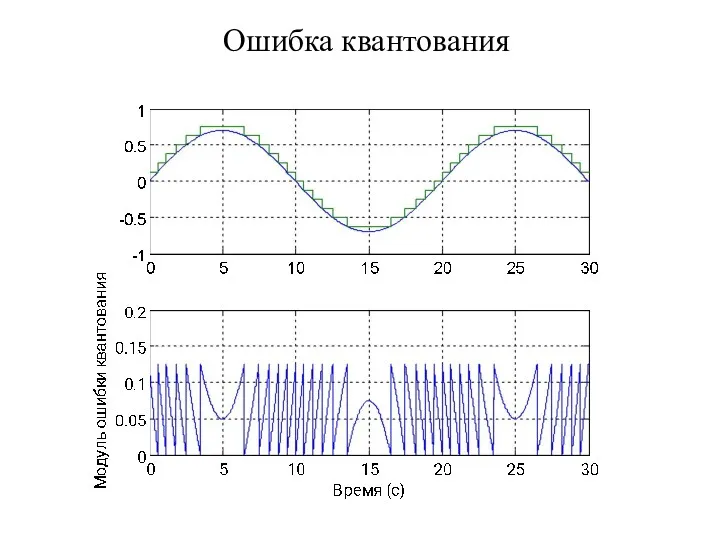
- 69. Ошибка квантования
- 70. Теорема Фурье Всякое периодическое колебание частоты F можно получить в результате суммирования бесконечного числа гармоник с
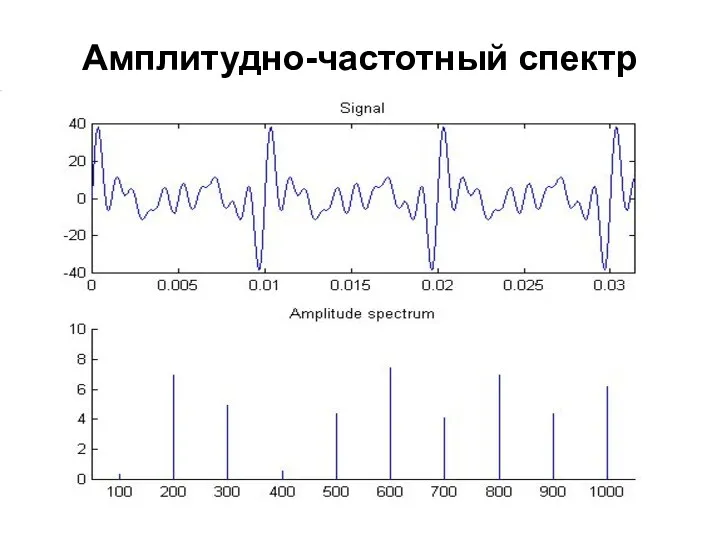
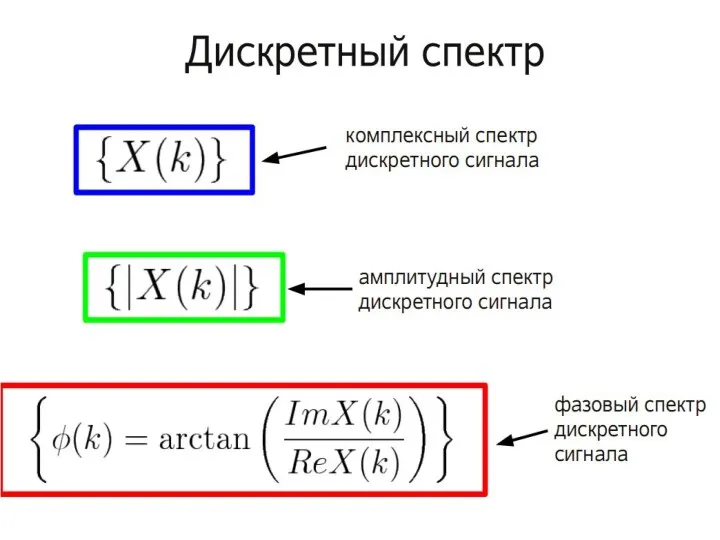
- 71. Амплитудно-частотный спектр
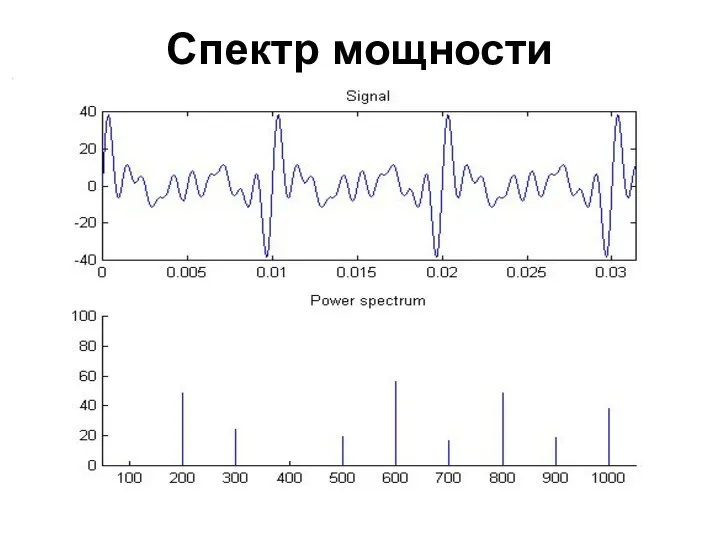
- 72. Спектр мощности
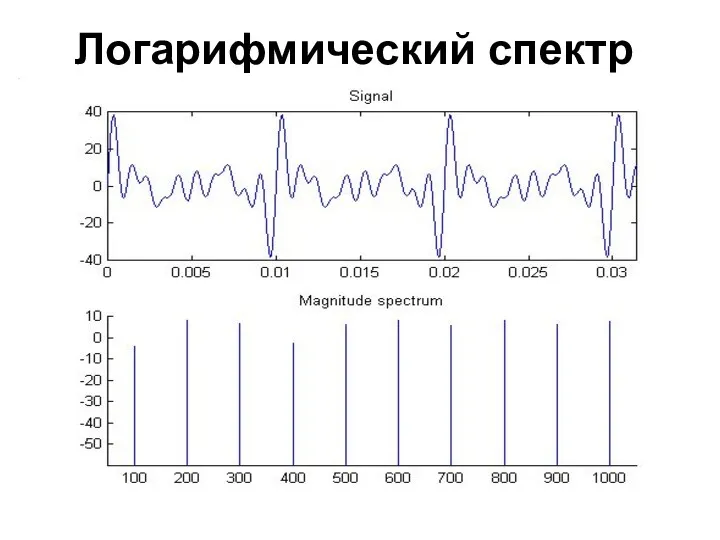
- 73. Логарифмический спектр
- 74. Перевод в децибеллы Имеем дискретный набор гармоник Для каждой гармоники считаем десятичный логарифм от амплитуды данной
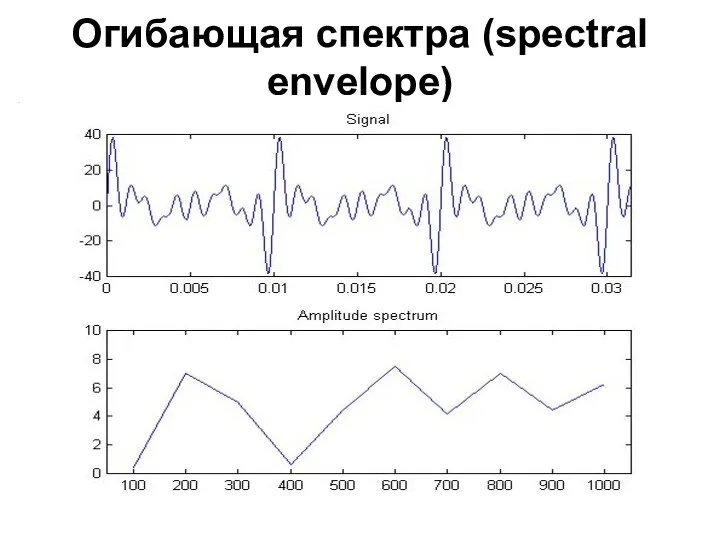
- 75. Огибающая спектра (spectral envelope)
- 76. Периодическое продолжение С точки зрения спектрального анализа дискретных сигналов, ЛЮБОЙ дискретный сигнал считается периодически продолженным
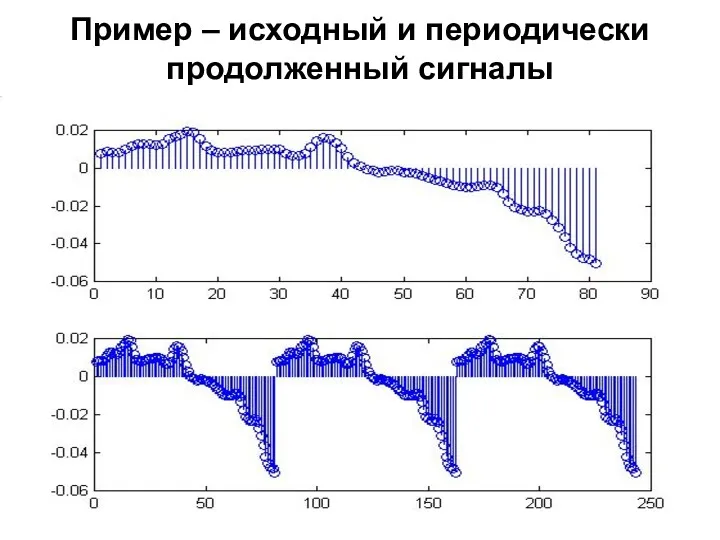
- 77. Пример – исходный и периодически продолженный сигналы
- 78. Периодическое продолжение Любой сигнал (вне зависимости от того, является ли он физически периодически или нет) рассматривается
- 79. Теорема Фурье Раз любой дискретный сигнал рассматривается как периодический (с периодом Т, равным длительности сигнала), то
- 80. Пример Пусть длительность Т анализируемого сигнала = 20 миллисекунд (0.02 секунд). Тогда сигнал может быть представлен
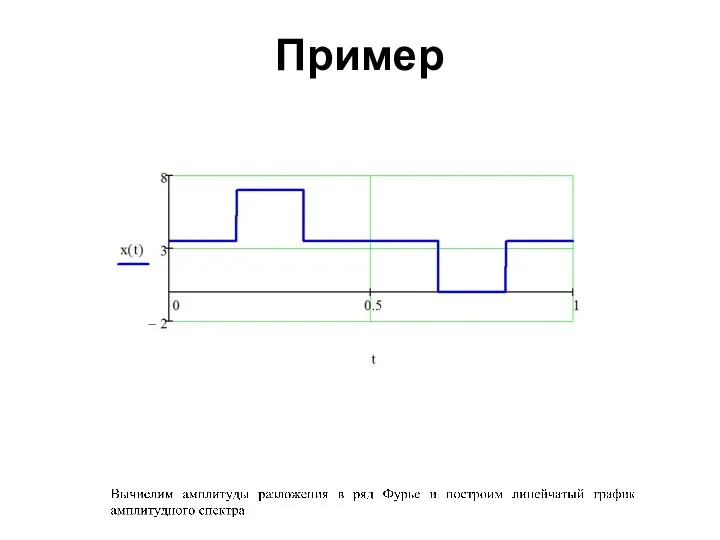
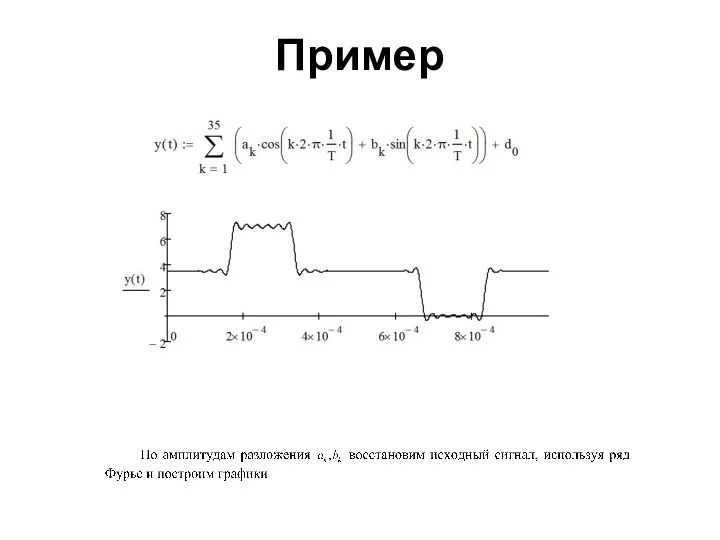
- 81. Пример
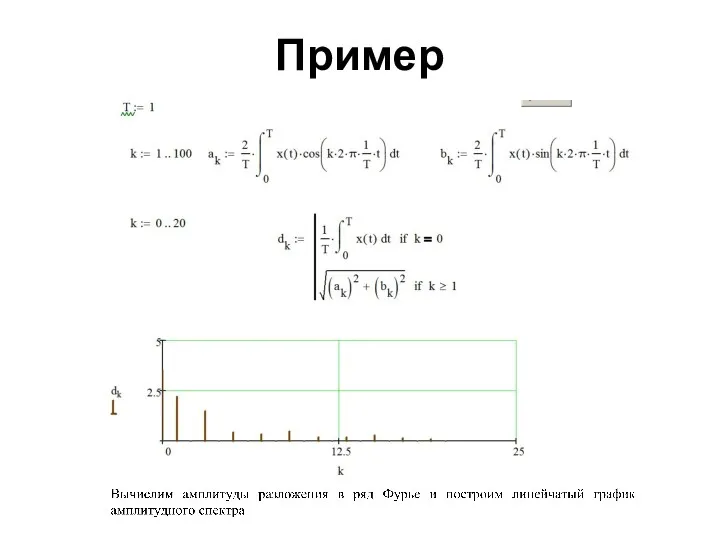
- 82. Пример
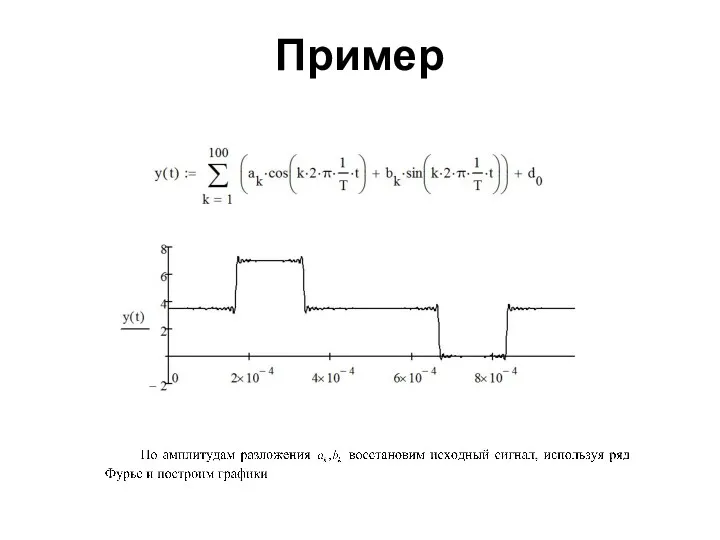
- 83. Пример
- 84. Пример
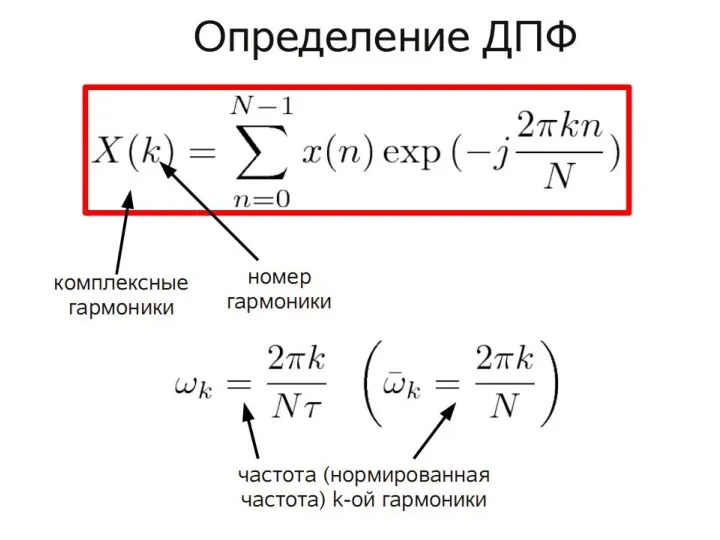
- 85. Дискретное преобразование Фурье Дискретное преобразование Фурье (ДПФ) (Discrete Fourier Transform, DFT) – результат применения теоремы Фурье
- 86. Дискретное преобразование Фурье (discrete Fourier transform, DFT) Имеем исходную последовательность N комплексных чисел (например, значения сигнала
- 87. Дискретное преобразование Фурье (discrete Fourier transform, DFT) Нормировочный множитель 1/N и знаки экспонент в DFT и
- 91. Пример ДПФ Пример: На интервале Т= [0,99], N=100, задан дискретный сигнал s(k) = δ(k-i) - прямоугольный
- 92. Быстрое преобразование Фурье Быстрое преобразование Фурье (БПФ) (Fast Fourier Transform, FFT) – способ «быстрого» вычисления ДПФ
- 93. Быстрое преобразование Фурье (БПФ) БПФ есть математически эквивалентный, но более быстрый алгоритм вычисления ДПФ. Основная идея
- 94. В чем трюк? Если длина сигнала в отсчетах есть степень двойки (например, 256 отсчетов = ,
- 95. БПФ Таким образом, для эффективного использования БПФ длина сигнала в отсчетах должна быть 64 или 128
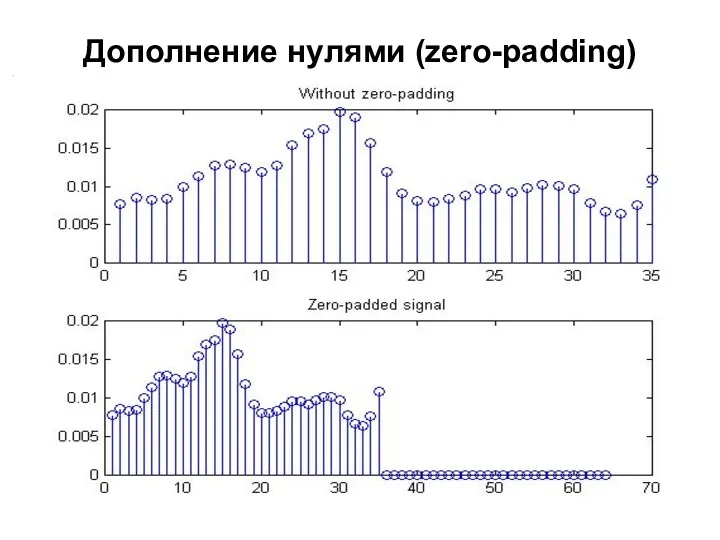
- 96. Дополнение нулями (zero-padding)
- 97. MATLAB Y = fft(x) - без дополнения нулями (может вычислять ОЧЕНЬ медленно, если длина сигнала x
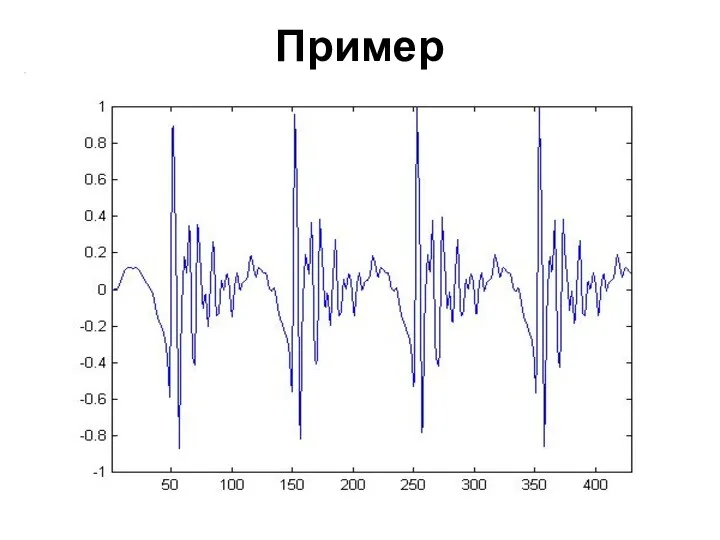
- 98. Пример
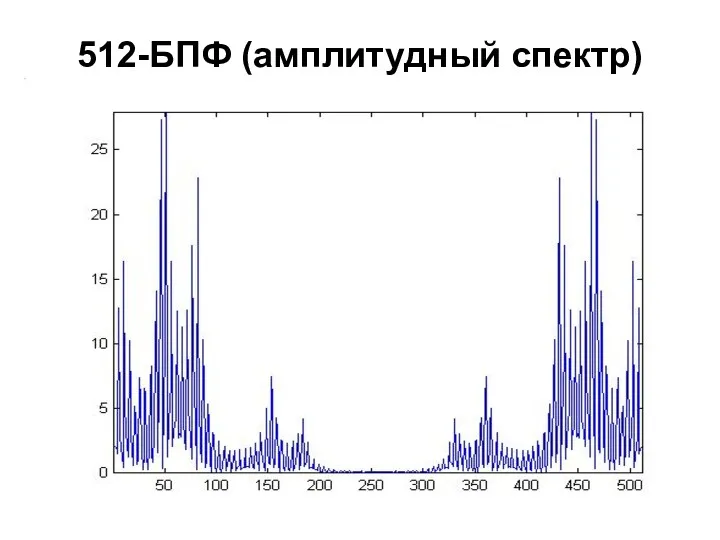
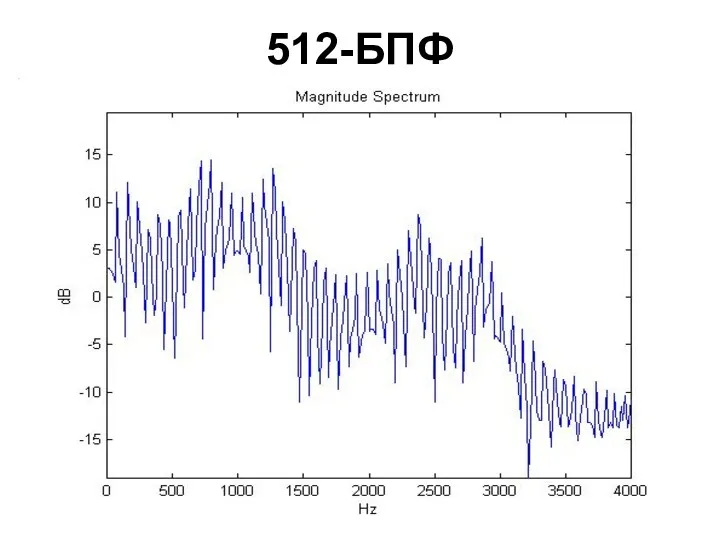
- 99. 512-БПФ (амплитудный спектр)
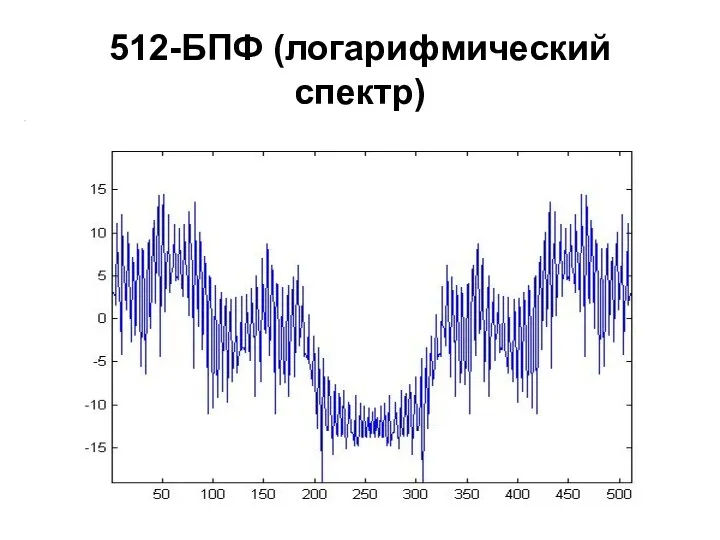
- 100. 512-БПФ (логарифмический спектр)
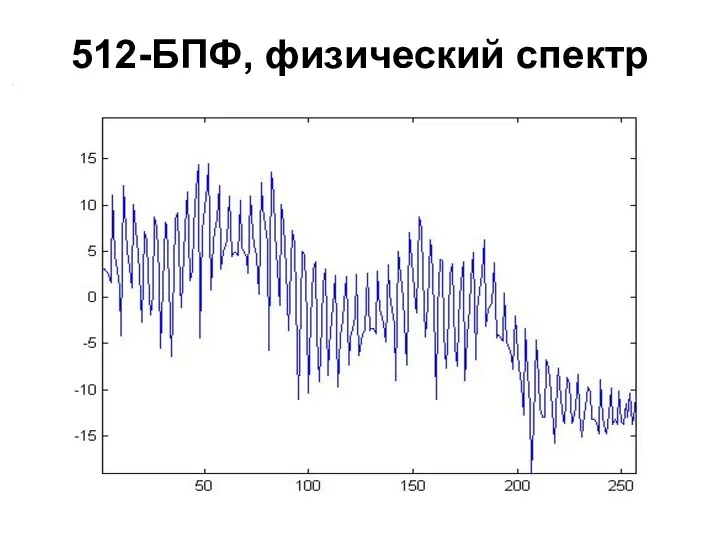
- 101. Свойство 3 БПФ-спектр симметричен относительно срединной гармоники (например, 256-й гармоники для 512-точечного БПФ) Соответствующая частота =
- 102. 512-БПФ, физический спектр
- 103. 512-БПФ
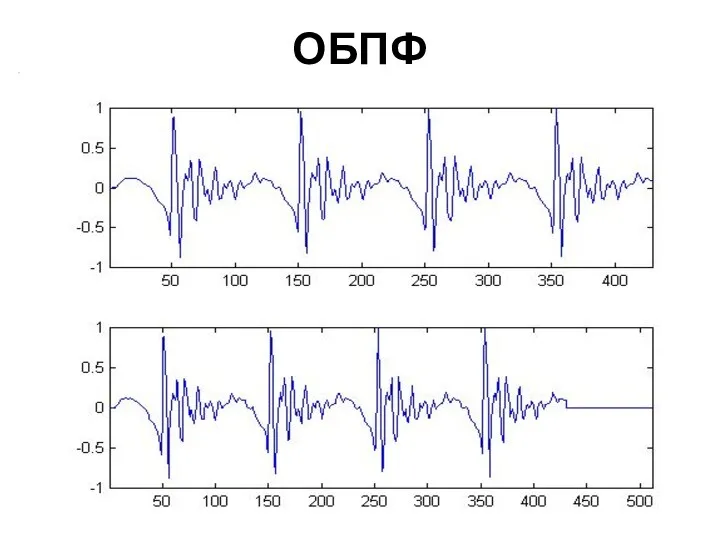
- 104. ОБПФ
- 105. Что нужно помнить Если длина сигнала в отсчетах = N, в секундах = Т, то сигнал
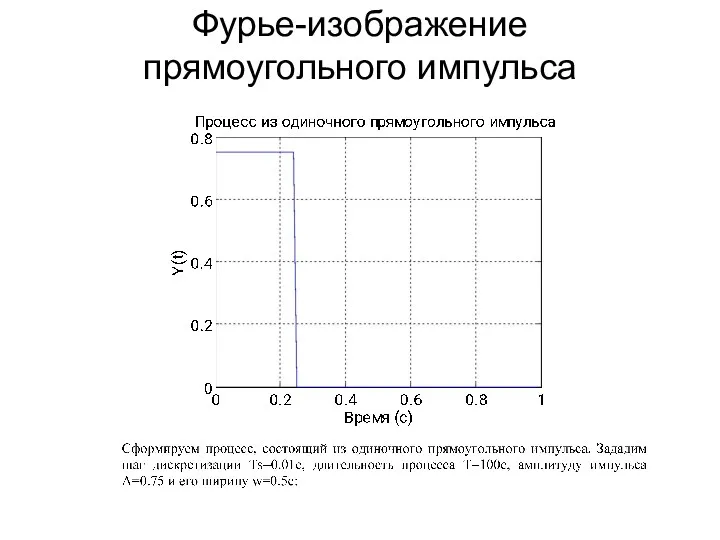
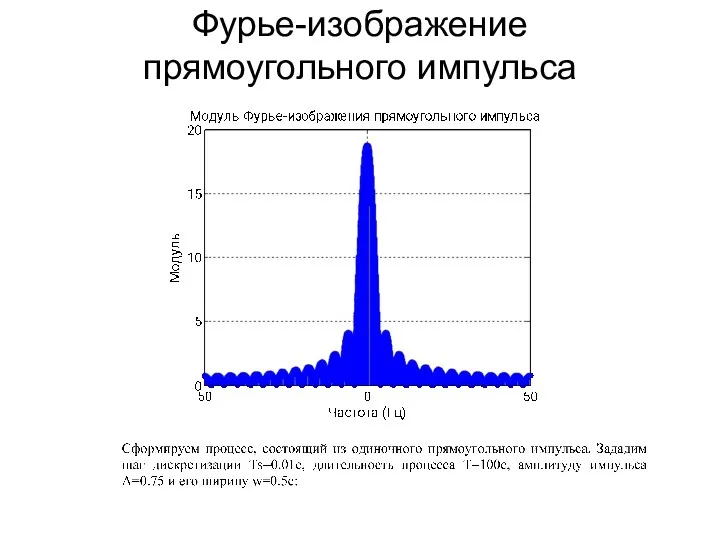
- 106. Фурье-изображение прямоугольного импульса
- 107. Фурье-изображение прямоугольного импульса
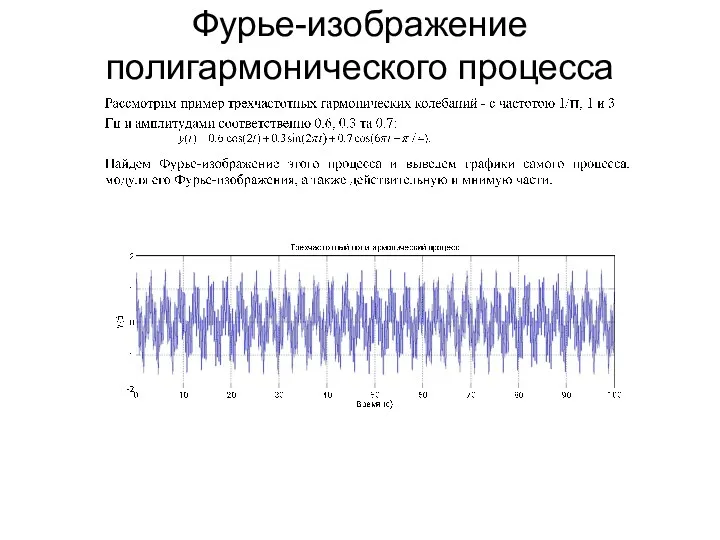
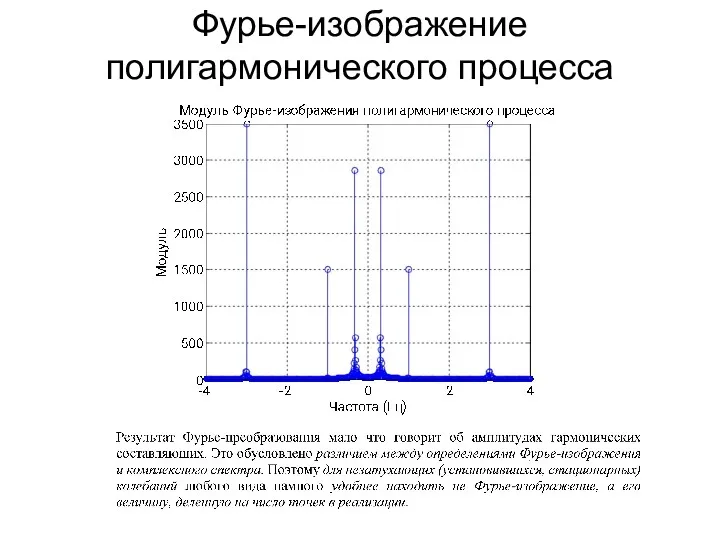
- 108. Фурье-изображение полигармонического процесса
- 109. Фурье-изображение полигармонического процесса
- 111. Скачать презентацию










![Пример sum_3harmonics([3,2,1],[0,0,0])](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/22212/slide-17.jpg)



































![Пример ДПФ Пример: На интервале Т= [0,99], N=100, задан дискретный](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/22212/slide-90.jpg)







 Ислам. Символ ислама. Молитва в исламе. Мечеть
Ислам. Символ ислама. Молитва в исламе. Мечеть fb-5fa0bf70
fb-5fa0bf70 олимпиада 2014
олимпиада 2014 Диоды Ганна
Диоды Ганна Физиология почки
Физиология почки Цикл уроков по теме Размножение
Цикл уроков по теме Размножение lesson 29
lesson 29 Физкультминутка
Физкультминутка Сказочный мир Гофмана Э. Т
Сказочный мир Гофмана Э. Т Искусственный интеллект в военном деле
Искусственный интеллект в военном деле Родительское собрание Как помочь ребенку стать внимательным? 2 класс
Родительское собрание Как помочь ребенку стать внимательным? 2 класс Край мой родной.
Край мой родной. Закаливание организма
Закаливание организма Давай откроем Мир друг другу
Давай откроем Мир друг другу Сценарий игры Большие маневры, посвященной Дню защитника Отечества
Сценарий игры Большие маневры, посвященной Дню защитника Отечества Дисциплина
Дисциплина Instagram. Как создать и продвинуть бренд с нуля
Instagram. Как создать и продвинуть бренд с нуля 9 класс. Электив. Уравнения.
9 класс. Электив. Уравнения. Стратегическое управление стоматологической клиникой на основе сбалансированной системы показателей эффективности. Часть 1
Стратегическое управление стоматологической клиникой на основе сбалансированной системы показателей эффективности. Часть 1 Microsoft Paint
Microsoft Paint Презентация Глиняная игрушка
Презентация Глиняная игрушка Музыка Возрождения (XV-XVI вв.)
Музыка Возрождения (XV-XVI вв.) Centrum logistyczne to jest wyspecjalizowana struktura
Centrum logistyczne to jest wyspecjalizowana struktura Боевое знамя воинской части
Боевое знамя воинской части Правоохранительные органы
Правоохранительные органы Время
Время Электронды техника ќўраушылары. Заттыѕ ќўрылысы туралы негізгі тїсініктер
Электронды техника ќўраушылары. Заттыѕ ќўрылысы туралы негізгі тїсініктер Наш кабинет - самый лучший кабинет России!
Наш кабинет - самый лучший кабинет России!