Содержание
- 2. Тематика курса Тема 1. Матрицы и операции над ними. Тема 2. Определители. Миноры и алгебраические дополнения.
- 3. Тематика курса Тема 6. Векторы и операции над ними. Координаты точек и векторов. Тема 7. Скалярное,
- 4. Матрицы и операции над ними Тема 1
- 5. План Определение матрицы. Виды матриц. Операции над матрицами. Свойства матричных операций. Транспонирование матрицы. Свойства операции транспонирования.
- 6. Определение матрицы. Виды матриц
- 11. Операции над матрицами
- 14. Свойства матричных операций 1) А+В=В+А 2) (А+В)+С=А+(В+С) 3) А+О=О+А=А 4) 1А=А1=А 5) 0А=А0=О; λО=Оλ=О 6) λ(μА)=(λμ)А
- 15. Свойства матричных операций 10) (А+В)С=АС+ВС 11) А(В+С)=АВ+АС 12) А(ВС)=(АВ)С 13) АЕ=ЕА=А 14) Если произведение АВ существует,
- 16. Транспонирование матрицы
- 18. Свойства операции транспонирования
- 19. Резюме Представлены основные определения и операции над матрицами и их свойства, являющиеся базовыми в теории матриц.
- 20. Определители. Миноры и алгебраические дополнения. Обратная матрица Тема 2
- 21. План Определитель квадратной матрицы. Свойства определителей. Миноры и алгебраические дополнения. Теорема о разложении определителя по строке
- 22. Определитель квадратной матрицы
- 27. Свойства определителей
- 30. Миноры и алгебраические дополнения
- 32. Теорема о разложении определителя по строке (столбцу)
- 35. Обратная матрица и её свойства
- 38. Матричные уравнения
- 41. Резюме Введены понятия определителя, минора, алгебраического дополнения и их свойства, играющие важную роль при решении систем
- 42. Системы линейных уравнений и методы их решения Тема 3
- 43. План Системы линейных алгебраических уравнений (СЛАУ) и их решения. Однородная система линейных уравнений. Метод Крамера для
- 44. Системы линейных алгебраических уравнений (СЛАУ) и их решения
- 46. Однородная система линейных уравнений
- 47. Метод Крамера для решения СЛАУ
- 54. Матричный метод решения СЛАУ
- 58. Эквивалентные системы
- 59. Элементарные преобразования систем 1. Перемена мест двух уравнений в системе; 2. Умножение обеих частей уравнения на
- 60. Ступенчатая система Система называется ступенчатой, если каждое уравнение имеет хотя бы 1 отличный от 0 коэффициент
- 61. Метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть
- 64. При этом система будет несовместной, если в процессе преобразований мы получим уравнение, в котором коэффициенты при
- 68. Резюме Рассмотрены основные методы решения системы линейных алгебраических уравнений, использующиеся в линейной алгебре и некоторых вопросах
- 69. Комплексные числа Тема 4
- 70. План Алгебраическая форма комплексного числа. Геометрическое изображение и тригонометрическая форма комплексного числа. Действия над комплексными числами,
- 71. Алгебраическая форма комплексного числа
- 75. Геометрическое изображение и тригонометрическая форма комплексного числа
- 79. Действия над комплексными числами, записанными в тригонометрической форме. Формула Муавра
- 83. Извлечение корня п-ой степени из комплексного числа. Корни из единицы. Первообразные корни
- 93. Показательная форма комплексного числа
- 96. Резюме Приведены основные результаты, касающиеся комплексных чисел, дана их алгебраическая и геометрическая интерпретация.
- 97. Многочлены степени п Тема 5
- 98. План Основные определения. Деление многочленов с остатком. Делимость многочленов. Свойства делимости. НОД. Алгоритм Евклида. Корни многочленов.
- 99. Основные определения
- 104. Деление многочленов с остатком
- 105. Делимость многочленов. Свойства делимости
- 108. НОД. Алгоритм Евклида
- 111. Корни многочленов. Теорема Безу. Схема Горнера
- 116. Кратные корни. Основная теорема алгебры
- 118. Резюме Приведены основные свойства, касающиеся делимости многочленов, даны основные результаты, связанные с нахождением корней многочленов.
- 119. Векторы и операции над ними. Координаты точек и векторов Тема 6
- 120. План Линейные операции над векторами. Базисы. Прямоугольные системы координат. Свойства координат точек и векторов. Полярная система
- 121. Вектор – это направленный отрезок, т.е. отрезок прямой, у которого указано, какой конец отрезка является началом,
- 122. Длиной вектора называется длина отрезка, изображающего этот вектор, направление определяется указанием начала и конца вектора. Параллельным
- 123. Два вектора а и b называются сонаправленными (или одинаково направленными), если при приложении к одной точке
- 124. Сонаправленные и противоположно направленные векторы образуют совокупность коллинеарных векторов; таким образом, векторы коллинеарны, если при приложении
- 125. Вектор а компланарен плоскости π ( ), если при приложении к какой-либо точке плоскости π вектор
- 126. Отношением двух коллинеарных векторов а и b, , называется число, определяемое так: Осью называется прямая, на
- 127. Пусть вектор а лежит на оси (или на прямой, параллельной оси), т.е. . Координатой вектора а
- 128. Приложим вектор к точке О, получим вектор , приложим вектор b к точке А, получим вектор
- 129. Замечания. 1) Всегда λа || а, если , то . 2) Пусть a|| b ), тогда
- 130. Противоположным к вектору а называется вектор (– а), имеющий такую же, как и вектор а длину,
- 131. Первая ось с единичным вектором называется осью абсцисс ОХ, вторая ось с единичным вектором – осью
- 132. Возьмём произвольную точку А и построим её проекцию на ось ОХ, для чего проведём через точку
- 133. При этом, если проекция лежит на положительной (отрицательной) полуоси ОХ, то ( ). Аналогично для ординаты
- 134. Проекцией на ось ОХ будет вектор , на ось ОY – вектор . Координатами вектора назовём
- 135. Основные свойства координат. 1) Пусть , ⇒ . 2)Пусть ⇒ . . Замечание. Если мы приложим
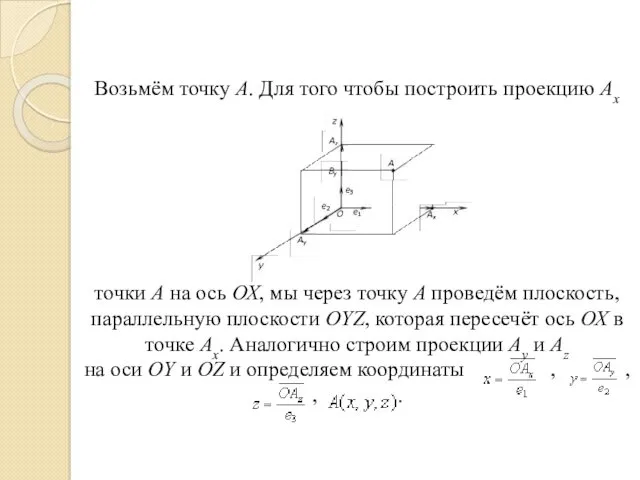
- 136. Возьмём точку А. Для того чтобы построить проекцию Ах точки А на ось ОХ, мы через
- 137. Для того чтобы построить проекции вектора , строим проекции его начала и конца и получаем на
- 138. Предложение 1. Пусть , , тогда . Рассмотрим задачу о делении отрезка в данном отношении. Пусть
- 139. Предложение 2. Пусть , ⇒ искомая точка М имеет координаты . Замечание. Особый интерес представляет случай,
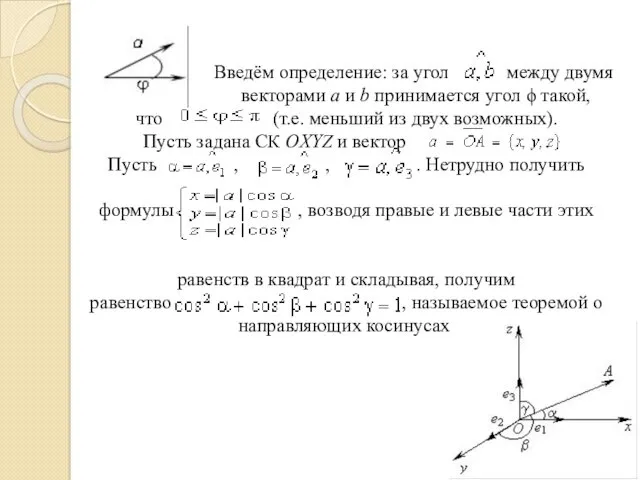
- 140. Введём определение: за угол между двумя векторами а и b принимается угол ϕ такой, что (т.е.
- 141. Замечание. На плоскости с системой координат ОХY, где и , мы получим формулы . Полезным для
- 142. Пусть , приложив его к началу координат О, имеем , , – проекции вектора а на
- 143. Замечание 2. Легко получить и формулу длины отрезка с концами и . Очевидно, что , учитывая,
- 144. Наряду с прямоугольными системами координат рассматриваются и другие системы координат. Наиболее важная из них – полярная
- 145. Положение каждой точки А определяется полярным радиусом и полярным углом ϕ – положительного поворота вокруг полюса
- 146. И наоборот: для прямоугольной СК ОХY определяем полярную СК, где ось ОХ совпадает с полярной осью,
- 147. Резюме Изучаются векторы и основные операции над ними. Определяются прямоугольные системы координат, вводятся координаты точек и
- 148. Скалярное, векторное и смешанное произведение векторов Тема 7
- 149. План Скалярное произведение векторов. Ориентация плоскости, пространства. Векторное произведение векторов. Смешанное произведение векторов. Объём ориентированного параллелепипеда.
- 150. Введём операцию скалярного произведения векторов. Скалярным произведением любых двух векторов а и b называется число ,
- 151. Предложение 1. . Доказательство. Представим тогда и с учётом свойств скалярного произведения, получим: Так как векторы
- 154. Будем вводить понятие ориентации плоскости и пространства. Рассмотрим на плоскости упорядоченную пару неколлинеарных векторов а и
- 155. В пространстве рассмотрим упорядоченную тройку некомпланарных векторов а, b, с. тройка векторов а, b, с будет
- 156. Определим операцию векторного произведения векторов. Пусть имеется упорядоченная пара векторов а и b. Векторным произведением [a,
- 159. Если векторы а и b заданы координатами: то вектор , где для вычисления которых можно использовать
- 160. Зная координаты векторного произведения, можно получить формулу для вычисления площади параллелограмма, построенного на векторах а и
- 161. Смешанное произведение векторов
- 162. Объём ориентированного параллелепипеда
- 164. Свойства смешанного произведения. 1) Смешанное произведение не меняется при круговой перестановке векторов: , т.к. при этом
- 165. 4) ⇔ векторы a,b,c компланарны – только в этом случае мы получим параллелепипед нулевого объёма. В
- 166. Введём прямоугольную СК ОXYZ. Получим формулы, выражающие смешанное произведение векторов через их прямоугольные координаты. Пусть по
- 167. Резюме Скалярное, векторное и смешанное произведения векторов, их свойства, представление в прямоугольных координатах представляют собой основной
- 168. Прямая на плоскости Тема 8
- 169. План Линии первого порядка. Теорема о линиях первого порядка. Различные уравнения прямой. Параллельность вектора и прямой
- 170. Напомним определение. Пусть на плоскости (или в пространстве) задана CK OXY (соответственно OXYZ). Будем говорить, что
- 171. Уравнение вида Ax+By+C=0 (Ax+By+Cz+D=0), называются уравнениями 1-го порядка, если (соответственно ), а линии (поверхности), которые они
- 173. Теорема о линиях первого порядка
- 174. Наоборот, если имеется прямая d, проходящая через точку и имеющая направляющий вектор , то для любой
- 175. Замечание 2. Отметим характеристики прямой d в зависимости от значений коэффициентов А, В, С в её
- 176. Рассмотрим различные уравнения прямой. Пусть прямая задана точкой и направляющим вектором , для любой точки на
- 179. Если прямая задана общим уравнением , то взяв за направляющий вектор , получим, что угловой коэффициент
- 180. Если задана точка А на оси ОХ (В на оси OY), то величиной отрезка ОА (ОВ)
- 181. Пусть теперь – точки пересечения прямой с осями ОХ и ОY соответственно, подставляя координаты точек А
- 182. Параллельность вектора и прямой, нормали прямой
- 183. Действительно, вектор будет перпендикулярен прямой тогда, когда он перпендикулярен какому-либо направляющему вектору этой прямой. Возьмём направляющий
- 184. Пусть прямая задана общим уравнением , вектор называется нормалью прямой. Прямая делит плоскость на две полуплоскости.
- 185. Предложение 3. Если , то точка М лежит в положительной полуплоскости; – точка М лежит в
- 186. Расположение двух прямых и углы между ними
- 188. Следствие. Для двух параллельных прямых всегда можно довести их общие уравнения до вида, отличающегося только свободными
- 190. Резюме Доказывается теорема о том, что линии первого порядка - прямые и только они. Рассматриваются различные
- 191. Прямая в пространстве Тема 9
- 192. План Основные уравнения прямой в пространстве. Расстояние от точки до прямой. Расположение двух прямых в пространстве.
- 193. Основные уравнения прямой в пространстве
- 194. Расстояние от точки до прямой
- 195. Расположение двух прямых в пространстве
- 198. Расстояние между двумя прямыми в пространстве
- 200. Резюме Изучаются различные уравнения прямой в пространстве. Получены формулы расстояния от точки до прямой, между двумя
- 201. Плоскость в пространстве Тема 10
- 202. План Теорема о поверхностях первого порядка. Уравнения плоскости при различных её заданиях. Параллельность вектора и плоскости,
- 203. Теорема о поверхностях первого порядка
- 204. Теорема 1. Поверхности первого порядка – плоскости и только они. Плоскость в пространстве можно задавать различными
- 205. Уравнения плоскости при различных её заданиях
- 209. Параллельность вектора и плоскости, нормали плоскости
- 214. Условием перпендикулярности плоскостей будет равенство Каждая плоскость делит пространство на два полупространства: положительное – то, куда
- 218. Резюме Доказывается теорема о том, что поверхности первого порядка – плоскости и только они. Рассмотрены различные
- 219. Смешанные задачи на прямую и плоскость в пространстве Тема 11
- 220. План Углы между прямой и плоскостью. Расположение прямой и плоскости в пространстве. Литература Александров П.С. Лекции
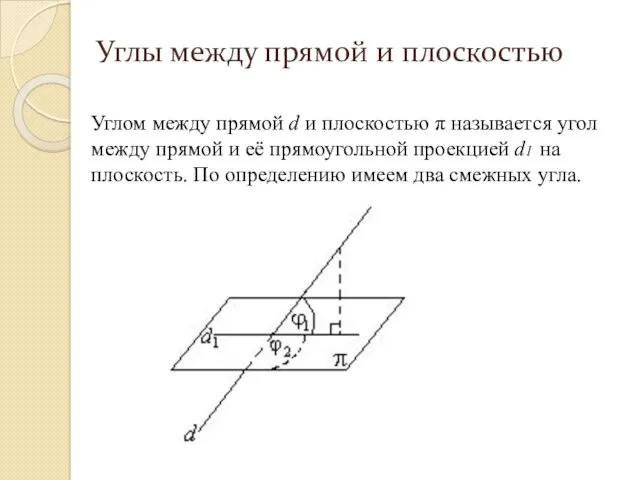
- 221. Углом между прямой d и плоскостью π называется угол между прямой и её прямоугольной проекцией d1
- 223. Доказательство.
- 224. Расположение прямой и плоскости в пространстве
- 226. Резюме Получены формулы, позволяющие судить о расположении прямой и плоскости, вычислять углы между прямой и плоскостью.
- 227. Кривые второго порядка, заданные канонически Тема 12
- 228. План Каноническое уравнение эллипса и его свойства. Каноническое уравнение гиперболы и её свойства. Каноническое уравнение параболы
- 229. Каноническое уравнение эллипса и его свойства
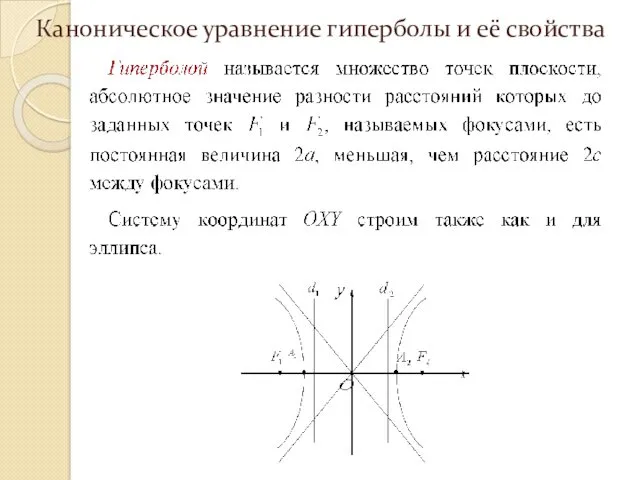
- 235. Каноническое уравнение гиперболы и её свойства
- 241. Каноническое уравнение параболы и её свойства
- 248. Скачать презентацию























































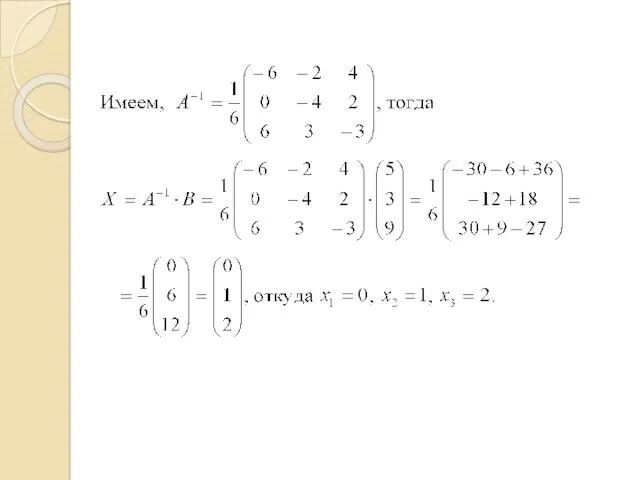
























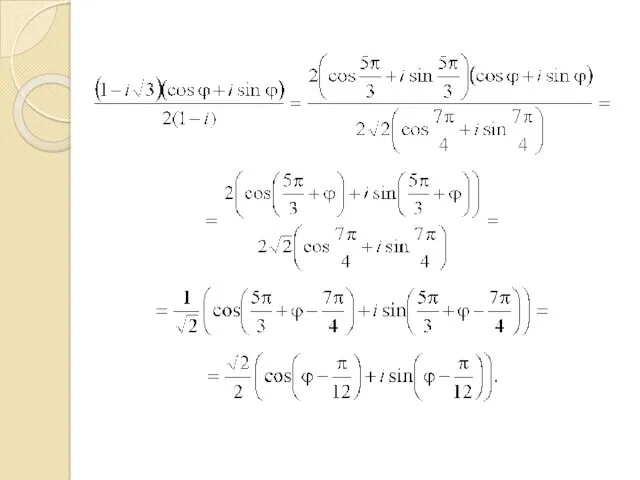



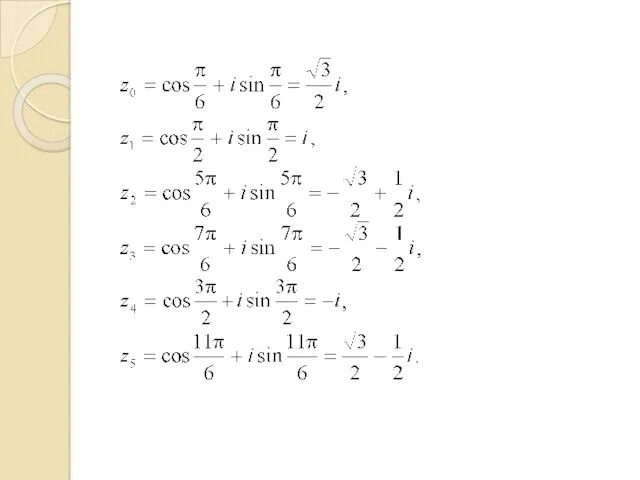




























































































































































 Пётр Ильич Чайковский (1840–1893)
Пётр Ильич Чайковский (1840–1893) 1917 год: от февраля к октябрю
1917 год: от февраля к октябрю Опорно-двигательная система человека. Скелет головы
Опорно-двигательная система человека. Скелет головы Презентация Лащенко
Презентация Лащенко Оксиды серы (IV) и (VI). Производство серной кислоты
Оксиды серы (IV) и (VI). Производство серной кислоты Государственный фонд развития промышленности Московской области
Государственный фонд развития промышленности Московской области Наблюдение за насекомыми
Наблюдение за насекомыми 16 ноября- Международный день толерантности
16 ноября- Международный день толерантности Занятие по дополнительной образовательной программе Микробиология для школьников по теме: Водоросли, их строение. Биологические особенности
Занятие по дополнительной образовательной программе Микробиология для школьников по теме: Водоросли, их строение. Биологические особенности Загрязнение гидросферы. Материалы к урокам географии и экологии.
Загрязнение гидросферы. Материалы к урокам географии и экологии. Л_1_СТ_Фізико_технічні_основи_променевої_діагностики_
Л_1_СТ_Фізико_технічні_основи_променевої_діагностики_ Конфликты и способы их разрешения.
Конфликты и способы их разрешения. Мораль. Человек и общество
Мораль. Человек и общество Периодический закон и периодическая система химических элементов.
Периодический закон и периодическая система химических элементов. Точность, взаимозаменяемость деталей и узлов столярных изделий
Точность, взаимозаменяемость деталей и узлов столярных изделий Podstawy finansów. Rachunek wyników
Podstawy finansów. Rachunek wyników Михаил Юрьевич Лермонтов 15 октября 1814 года – 27 июля 1841 года. Русский поэт, прозаик, драматург, художник
Михаил Юрьевич Лермонтов 15 октября 1814 года – 27 июля 1841 года. Русский поэт, прозаик, драматург, художник Денсаулық сақтауды жоспарлаудың, қаржыландырудың қазіргі кездегі проблемалары
Денсаулық сақтауды жоспарлаудың, қаржыландырудың қазіргі кездегі проблемалары Проект по строительству завода по производству высококачественных нефтепродуктов на территории Свердловской области
Проект по строительству завода по производству высококачественных нефтепродуктов на территории Свердловской области Згурський Петро. Студентський парламент
Згурський Петро. Студентський парламент Psikhologia_organizatsii_1
Psikhologia_organizatsii_1 Информационная система ЖИВУ.РФ
Информационная система ЖИВУ.РФ Отчёт о прохождении производственной практики в строительной компании ООО СК УРАЛПОЛ
Отчёт о прохождении производственной практики в строительной компании ООО СК УРАЛПОЛ Где логика? Интерактивная игра
Где логика? Интерактивная игра Роль и назначение международных стандартов финансовой отчетности (МСФО). Порядок создания МСФО
Роль и назначение международных стандартов финансовой отчетности (МСФО). Порядок создания МСФО Семь мудрецов Древней Греции
Семь мудрецов Древней Греции История престольного праздника День Святых Первоверховных апостолов Петра и Павла
История престольного праздника День Святых Первоверховных апостолов Петра и Павла Биологические науки. Интерактивный кроссворд
Биологические науки. Интерактивный кроссворд