Содержание
- 2. Литература: Карпелевич и Садовский. Элементы линейной алгебры и линейного программирования Красс и Чупрынов. Основы математики и
- 3. Системы линейных уравнений и неравенств
- 5. Пусть r = rank A = rank A Определение базисного решения
- 6. Метод Гаусса. Пример Прямой ход метода Гаусса
- 7. Обратный ход метода Гаусса
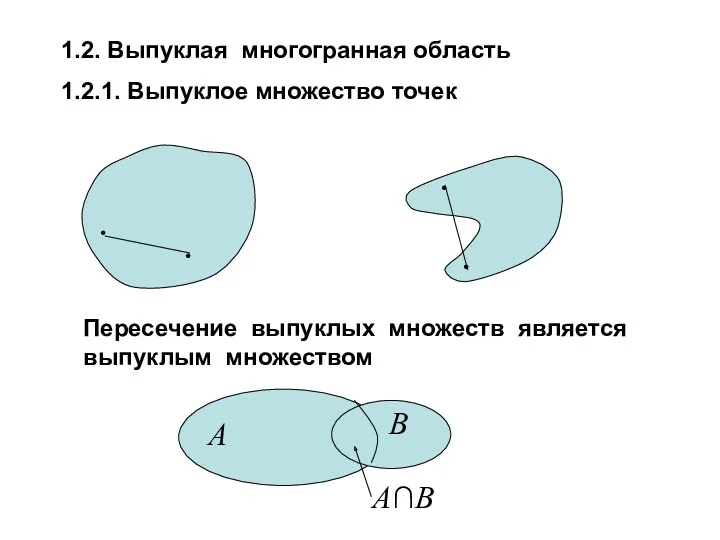
- 8. 1.2. Выпуклая многогранная область 1.2.1. Выпуклое множество точек • • • • Пересечение выпуклых множеств является
- 9. 1.2.3. Гиперплоскость, полупространство Примеры: 1. n=2 -- прямая -- полуплоскость
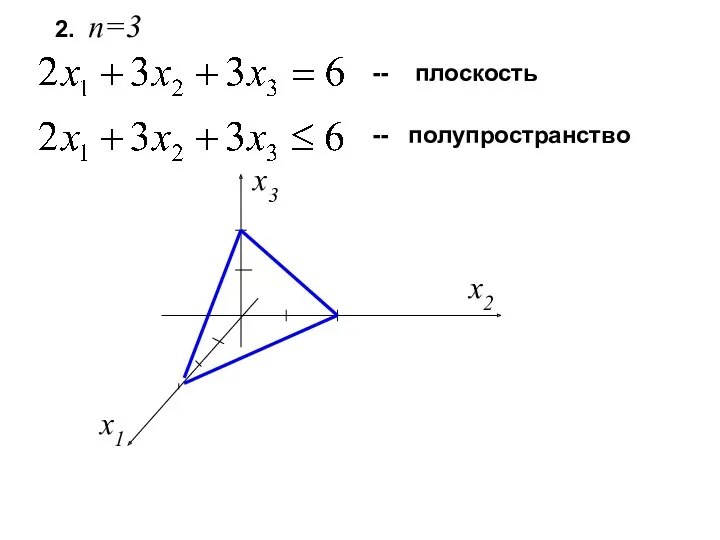
- 10. 2. n=3 -- плоскость -- полупространство x1 x2 x3
- 11. Полупространство является выпуклым множеством. Пересечение полупространств является выпуклым множеством. Система линейных неравенств задает в n-мерном пространстве
- 12. 1.3. Крайние (опорные) точки множества
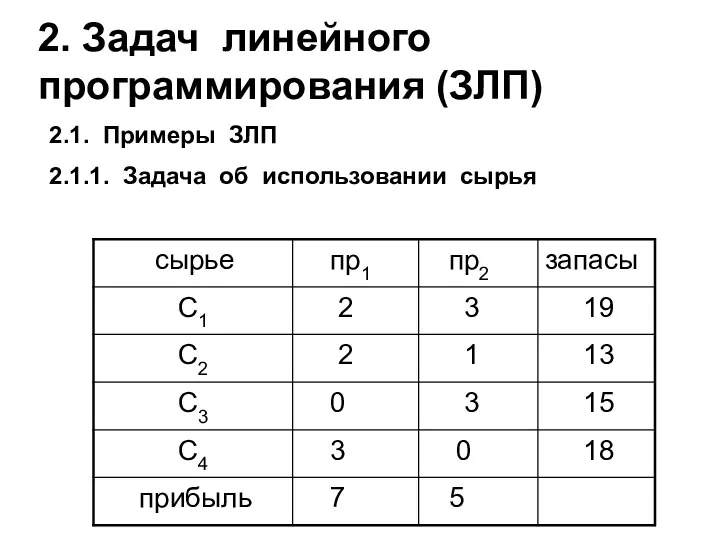
- 13. 2. Задач линейного программирования (ЗЛП) 2.1. Примеры ЗЛП 2.1.1. Задача об использовании сырья
- 14. Пусть x1 и x2 -- планируемый выпуск продукции Пр1 и Пр2 соответственно. Тогда
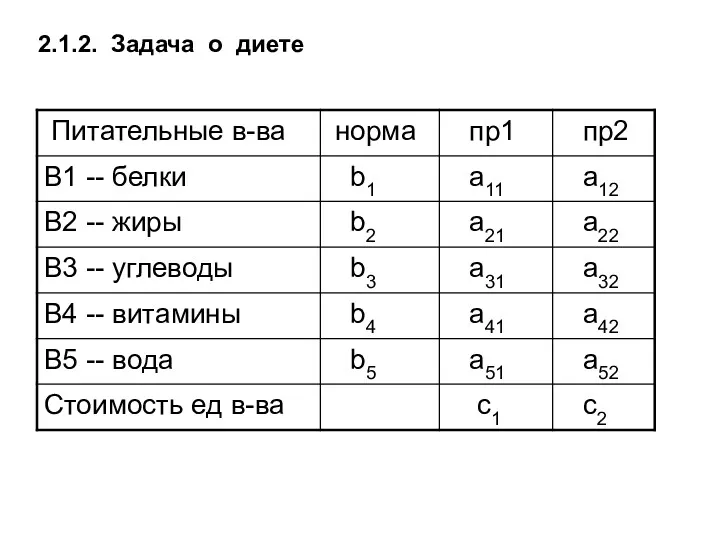
- 15. 2.1.2. Задача о диете
- 16. aij -- количество i-го питательного в-ва в 1 j-го продукта Пусть x1 и x2 -- планируемый
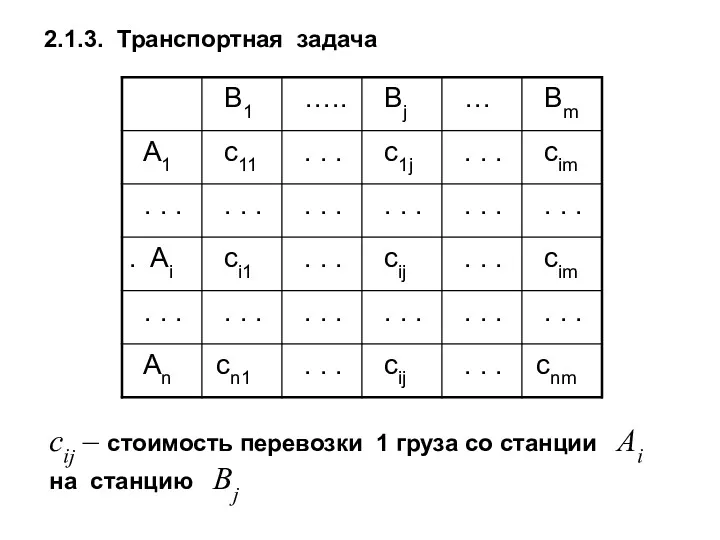
- 17. 2.1.3. Транспортная задача cij – стоимость перевозки 1 груза со станции Ai на станцию Bj
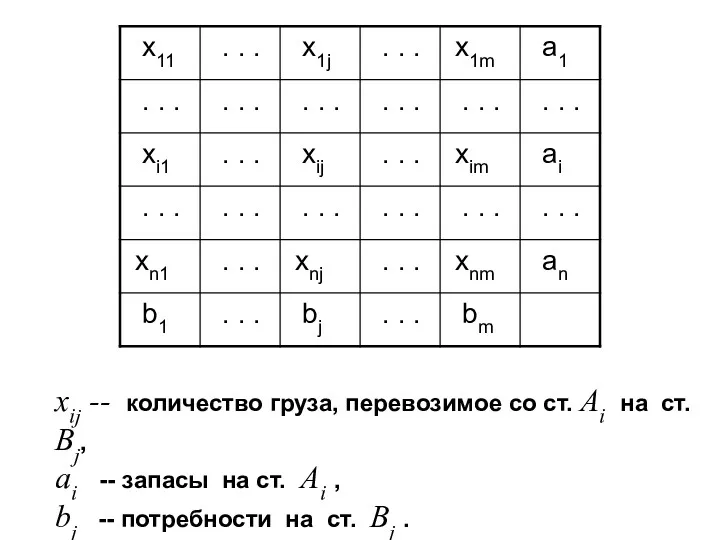
- 18. xij -- количество груза, перевозимое со ст. Ai на ст. Bj, ai -- запасы на ст.
- 19. Все запасы должны быть вывезены, и все потребности должны быть удовлетворены
- 20. 2.2. Виды ЗЛП 2.2.1. Общая ЗЛП (ОбЗЛП)
- 21. 2.2.2. Основная ЗЛП (ОсЗЛП)
- 22. 2.2.3. Каноническая ЗЛП (КЗЛП) 2.2.4. Переход от одного вида ЗЛП к другому КЗЛП → ОсЗЛП
- 23. Опуская левые неравенства, получим систему линейных уравнений
- 24. Пример
- 25. Опуская левые неравенства, получим систему линейных уравнений
- 26. ОсЗЛП → КЗЛП
- 27. Пусть r – ранг матрицы системы уравнений п.2.2.2. и имеется решение системы ограничений Опуская равенства слева,
- 28. Пример
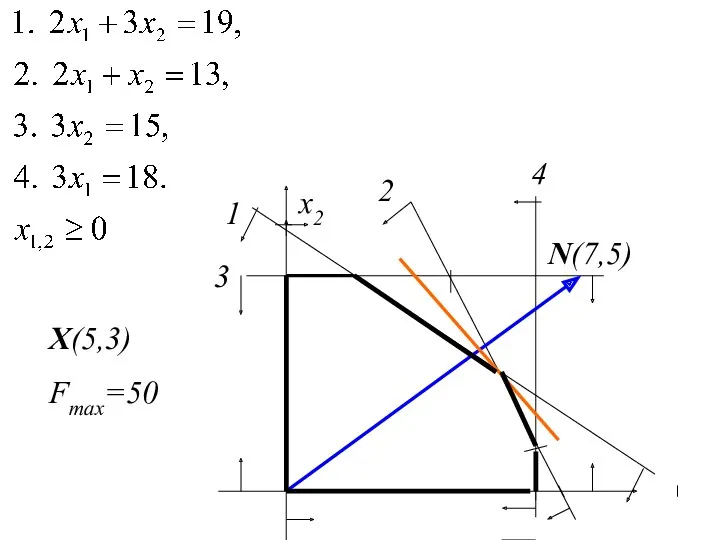
- 32. 3. Геометрический смысл ЗЛП и геометрический способ ее решения Рассмотрим КЗЛП. Среди всех точек замкнутой выпуклой
- 34. x2 1 2 3 4 N(7,5) X(5,3) Fmax=50
- 35. 4. Симплекс-метод 4.1. Перебор базисных решений Рассмотрим ОсЗЛП -- задачу об использовании сырья.
- 36. Увеличивая x1, мы уменьшаем F(x) x3, x4 ,x6 при этом уменьшаются и раньше всех обращается в
- 37. Увеличивая x2, мы уменьшаем F(x) x3, x4 ,x5 при этом уменьшаются и раньше всех обращается в
- 38. Увеличивая x6, мы уменьшаем F(x) x1, x3 ,x5 при этом уменьшаются и раньше всех обращается в
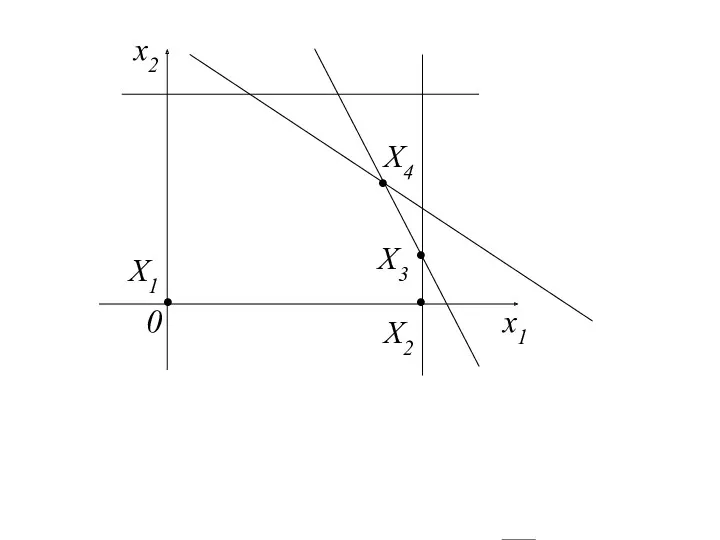
- 39. x2 0 x1 X1 X2 X3 X4 • • • •
- 40. 4.2. Алгоритм симплекс-метода 4.2.1. Найти исходное допустимое базисное решение 4.2.2. Выбрать свободную неизвестную, которая входит в
- 41. 4.3. Алгебра симплекс-метода. Симплекс-таблица 1. Записать исходное базисное решение и целевую функцию в стандартном виде
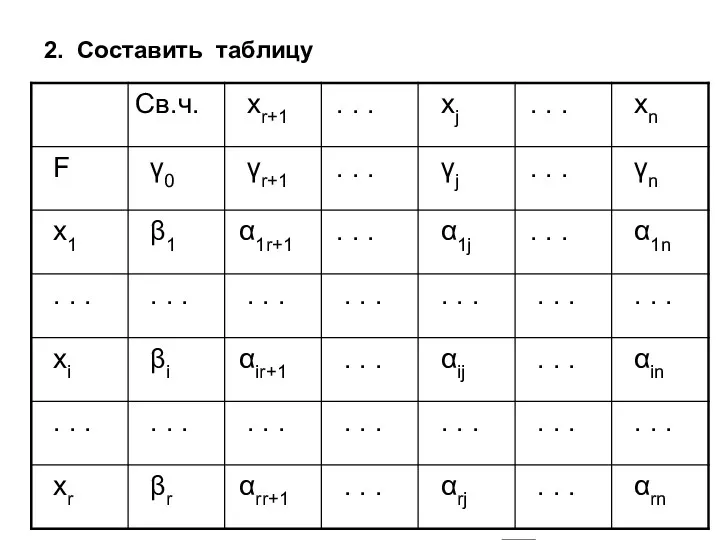
- 42. 2. Составить таблицу
- 43. Столбец xj называется генеральным столбцом, строка xi -- генеральной строкой, элемент αij -- генеральным элементом Правило
- 46. Правила пересчета симплекс-таблицы: • на месте генерального элемента пишется величина, ему обратная • все элементы генеральной
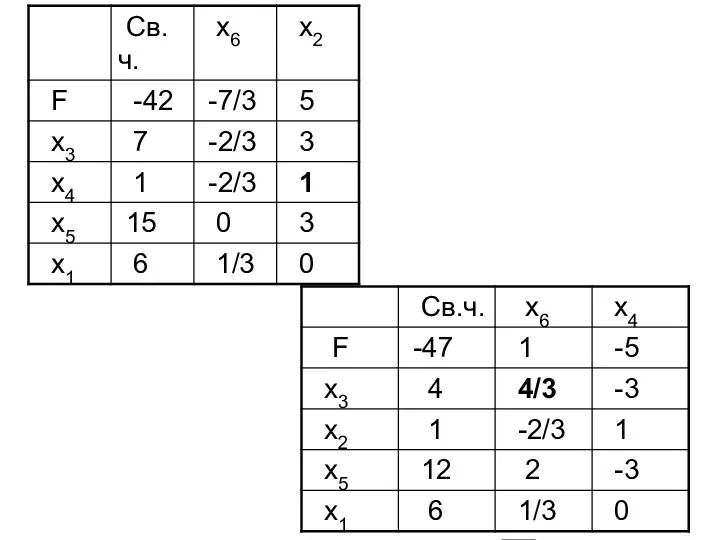
- 47. 4.4. Порядок работы по симплекс-методу 4.4.1. Найти исходное допустимое базисное решение. 4.4.2. Записать найденное решение в
- 48. Пример: Задача об использования сырья
- 50. 4.5. Теорема. При решении ОсЗЛП симплекс-методом за конечное число шагов мы приходим либо к оптимальному решению,
- 51. 5. М-метод (метод искусственного базиса) Пусть имеется ОсЗЛП Рассмотрим систему уравнений Можно считать, что все правые
- 52. Введем новые переменные И рассмотрим следующую ОсЗЛП M -- достаточно большое положительное число
- 53. Построенная задача называется M—задачей. 5.1. Основные теоремы Теорема 1. Если M—задача имеет оптимальное решение, в котором
- 54. Теорема 3. Если M—задача оптимального решения не имеет, то исходная задача также оптимального решения не имеет.
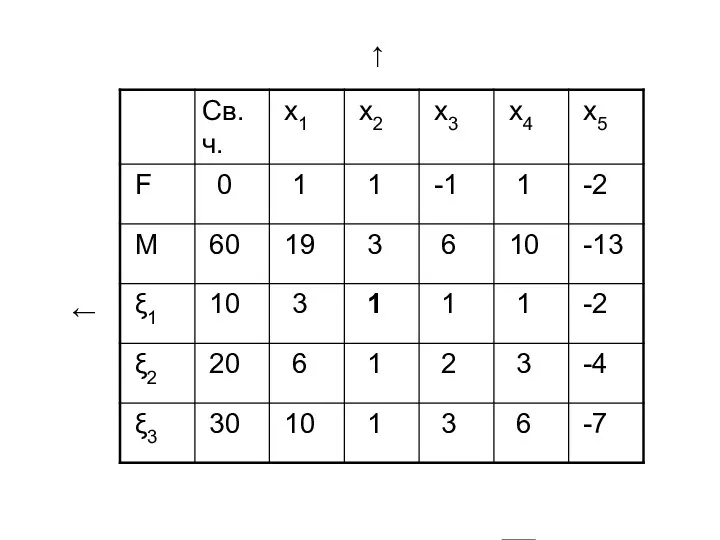
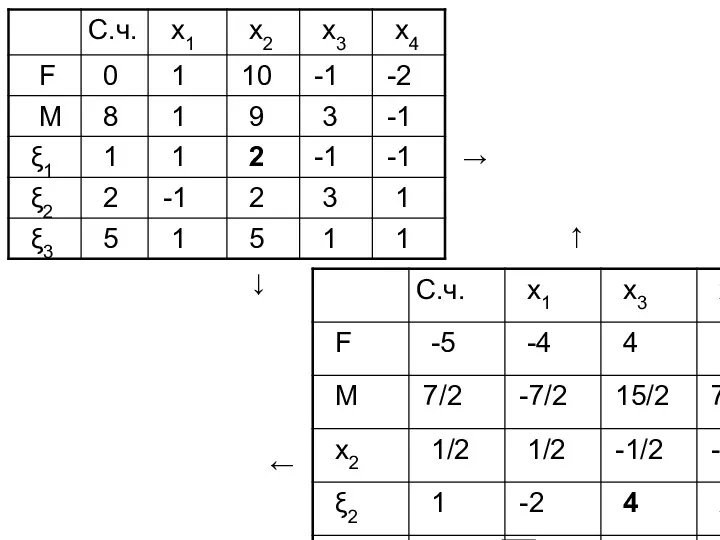
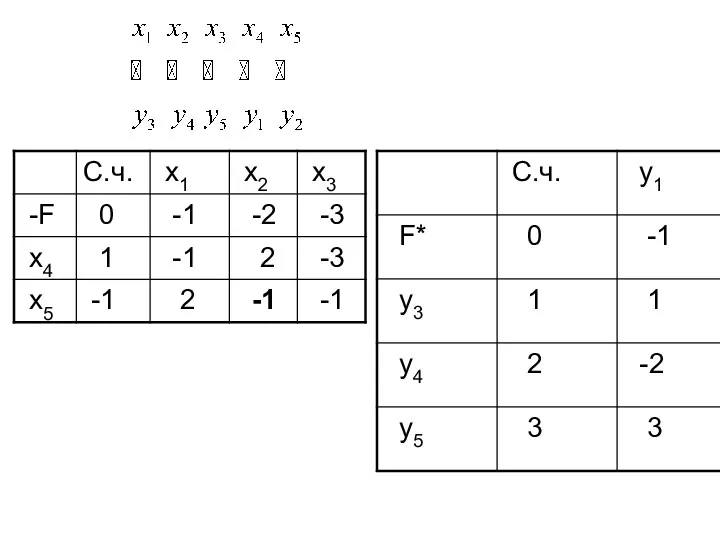
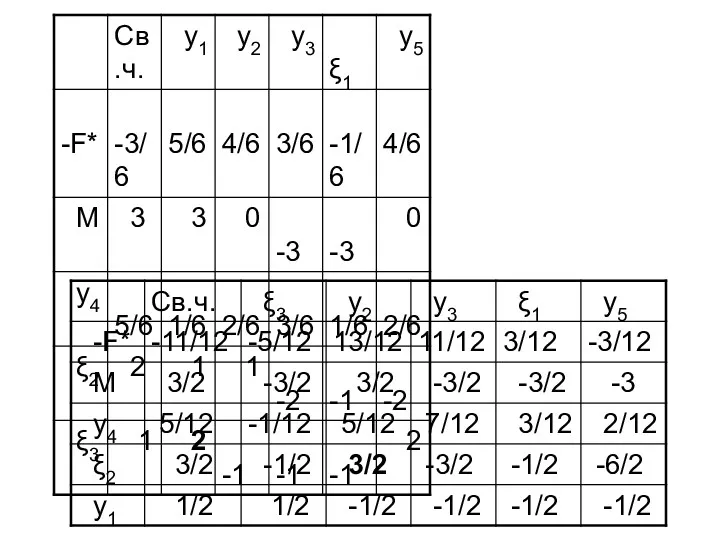
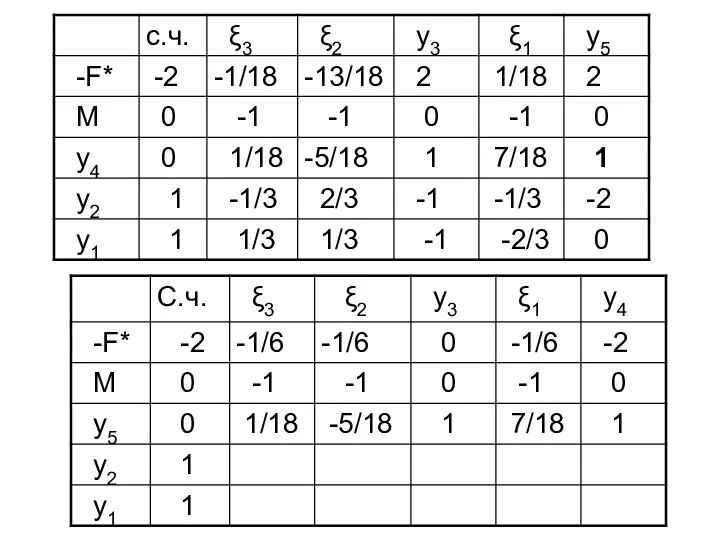
- 55. Составим M--задачу Симплекс-таблица:
- 56. ← ↑
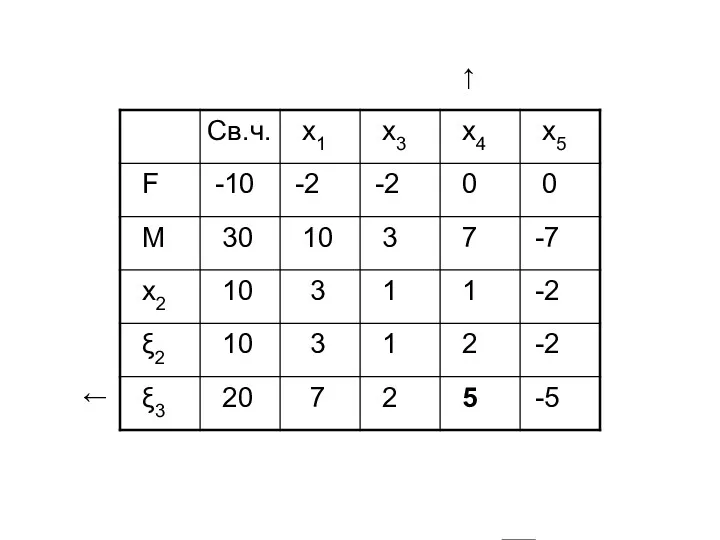
- 57. ← ↑
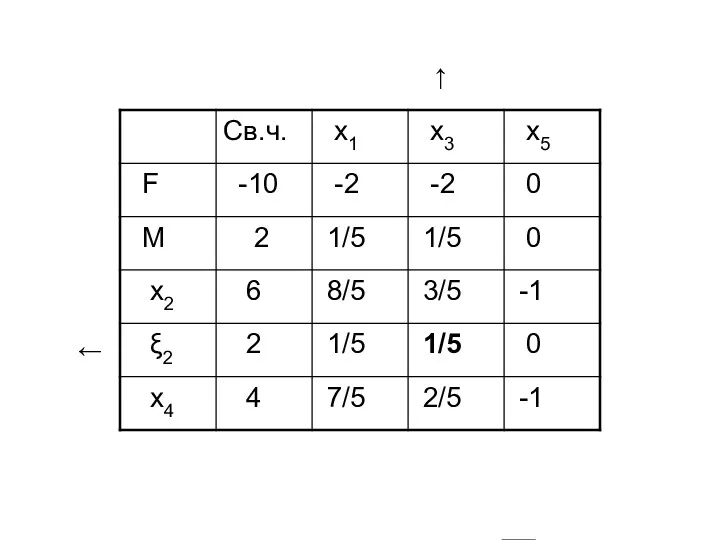
- 58. ← ↑
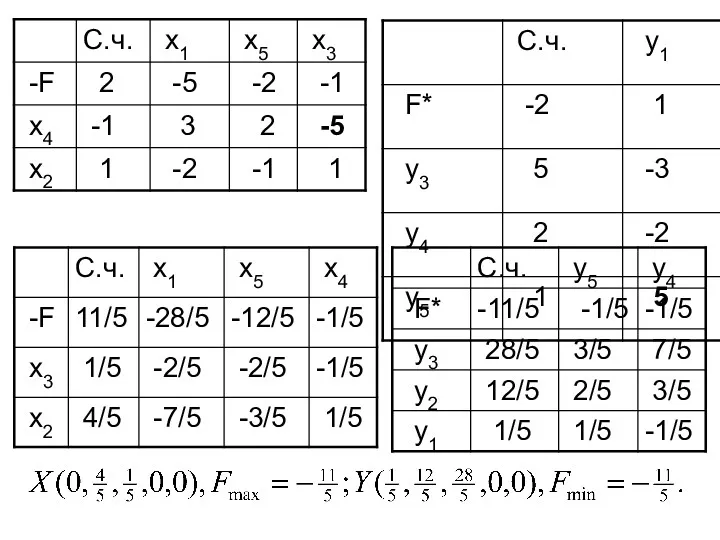
- 60. 2. Составим M—задачу и симплекс-таблицу
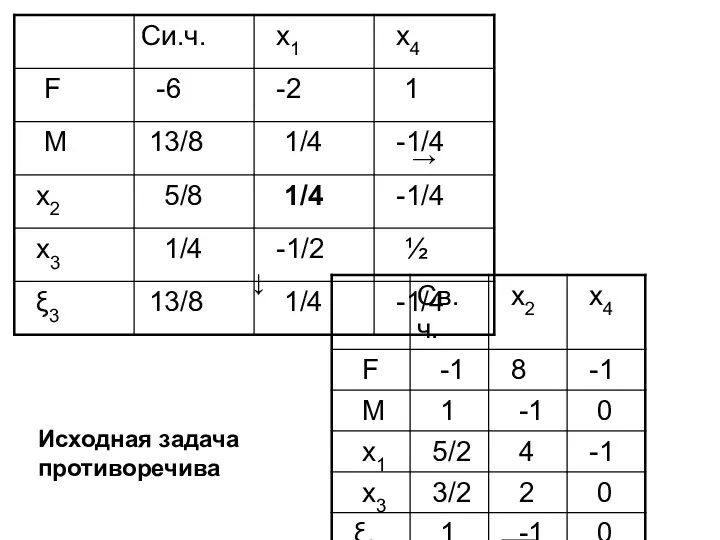
- 62. → ↓ ← ↑
- 63. → ↓ Исходная задача противоречива
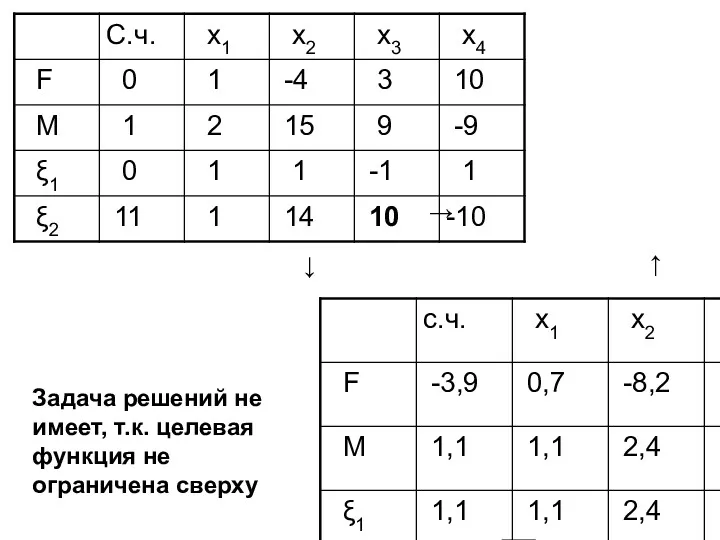
- 64. 3. M-задача
- 65. ↓ → ↑ Задача решений не имеет, т.к. целевая функция не ограничена сверху
- 66. 6. Теория двойственности
- 68. 6.1. Задача, двойственная к КЗЛП По определению 1. Каждой переменной исходной задачи соответствует ограничение двойственной задачи
- 69. 7. Коэффициенты при неизвестных в целевой функции двойственной задачи совпадают с правыми частями системы ограничений исходной
- 70. Исходная КЗЛП Двойственная задача Двойственная КЗЛП
- 71. Двойственная к двойственной КЗЛП
- 72. 6.2. Задача, двойственная к ОбЗЛП 1. Все ограничения-неравенства согласованы со способом оптимизации целевой функции, а именно,
- 73. 6. Ограничения, соответствующие неотрицательным переменным исходной задачи должны иметь вид неравенств противоположного смысла по сравнению с
- 74. Пример:
- 76. 6.3. Теоремы теории двойственности Первая теорема двойственности 2. Основное неравенство теории двойственности Если, например, F(x) →
- 78. 3. Вторая теорема двойственности Пусть имеются два допустимых решения двух взаимно двойственных задач. Для того, чтобы
- 79. 6.3. Решение двух взаимно двойственных задач 1. Составить двойственную задачу, решить ее и Восстановить решение исходной
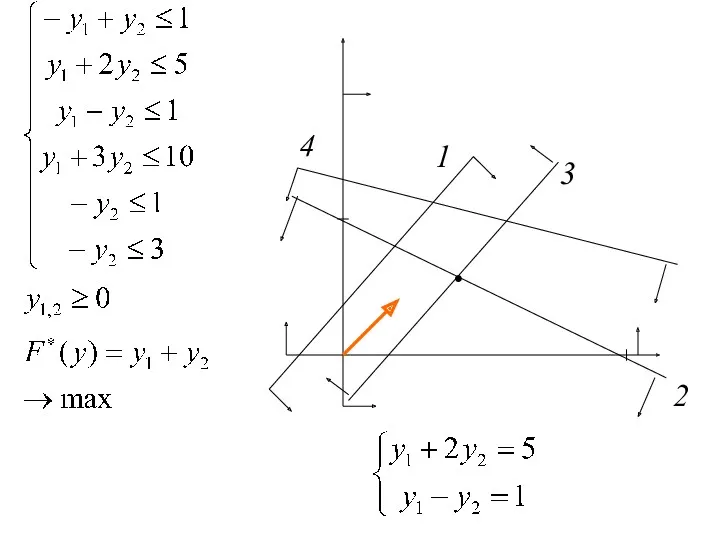
- 80. • 4 1 3 2
- 82. 2. Двойственный симплекс-метод
- 85. 3. Двойственный М-метод
- 91. Скачать презентацию


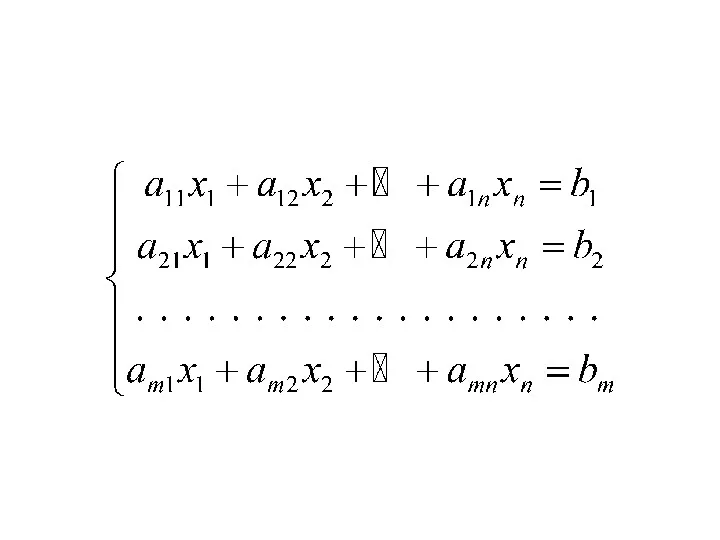













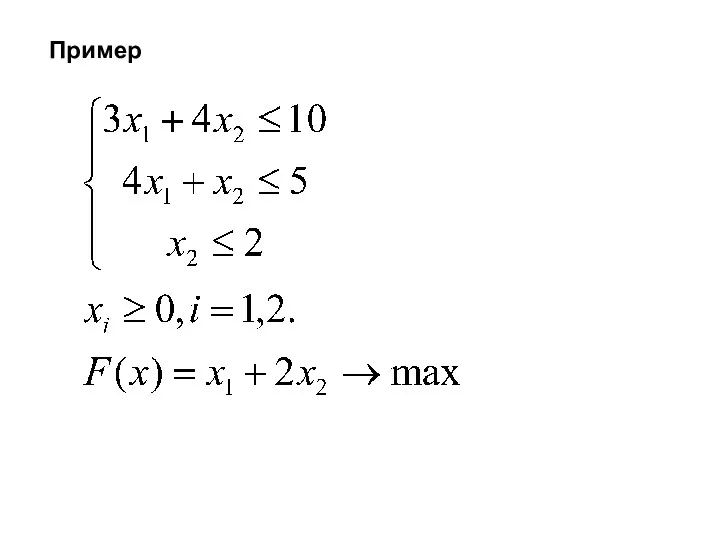

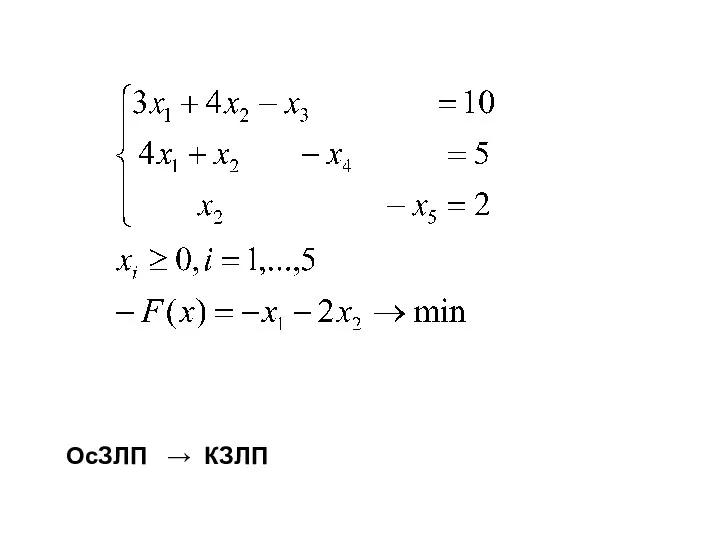

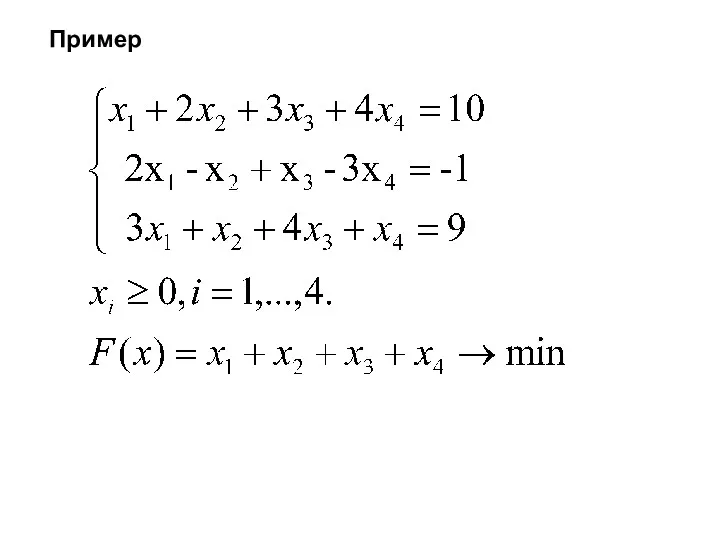
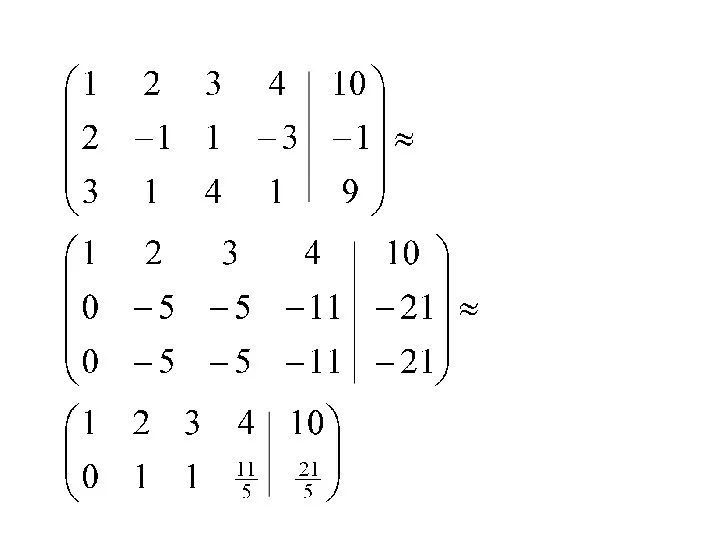
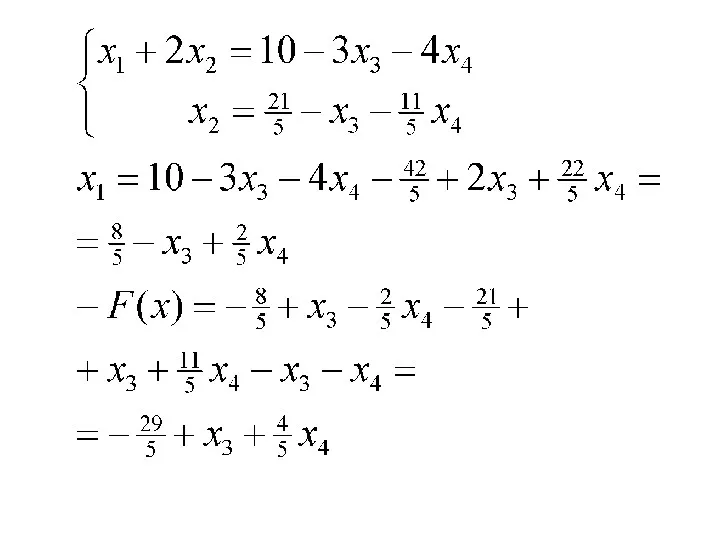
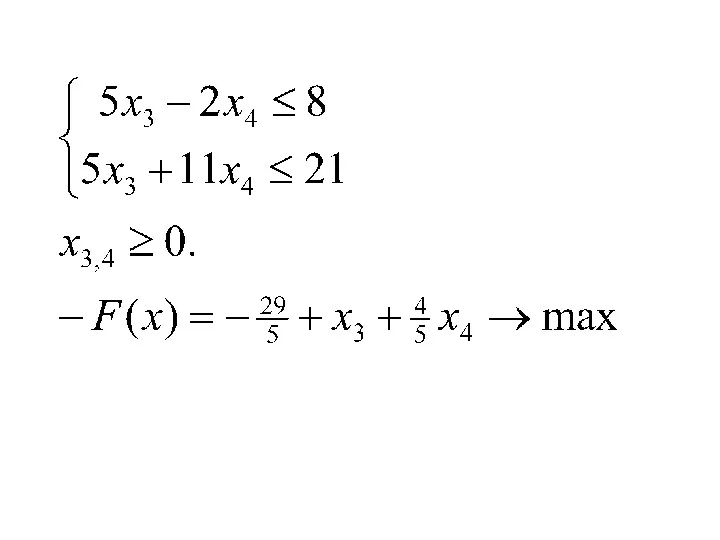

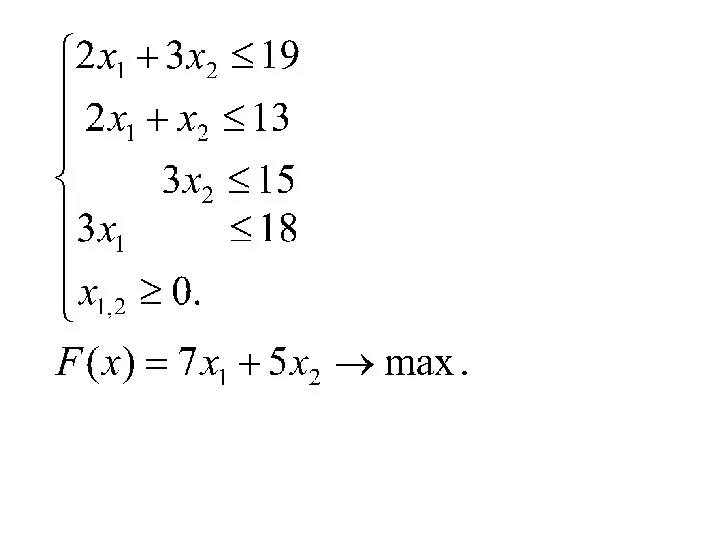







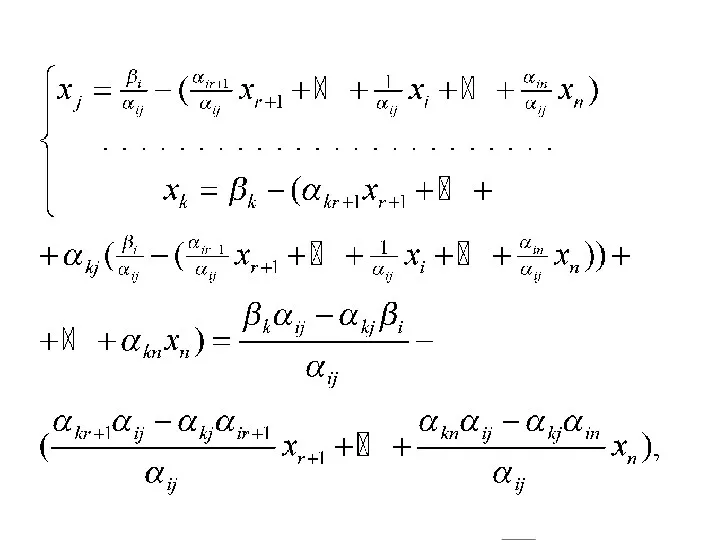
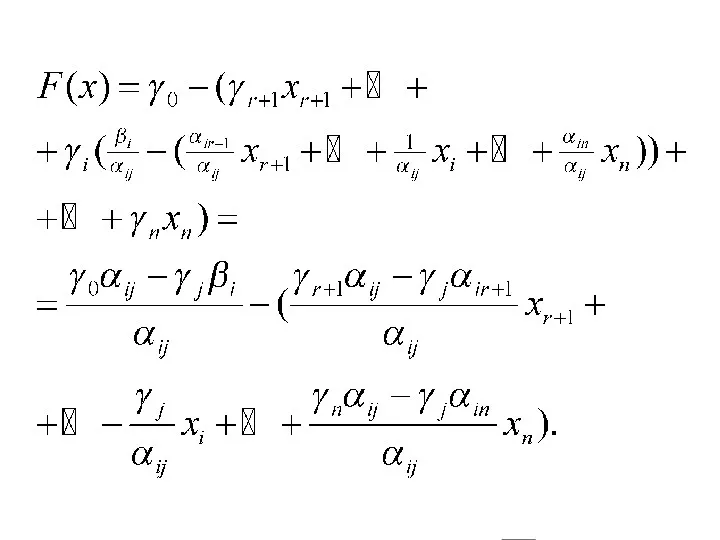











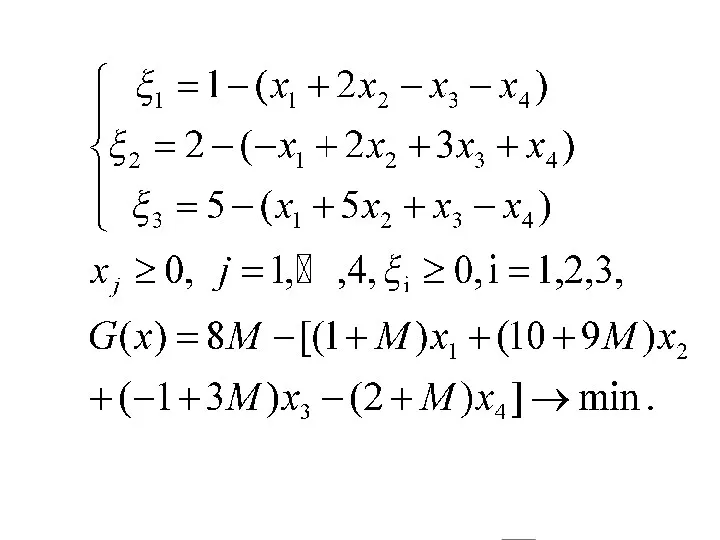
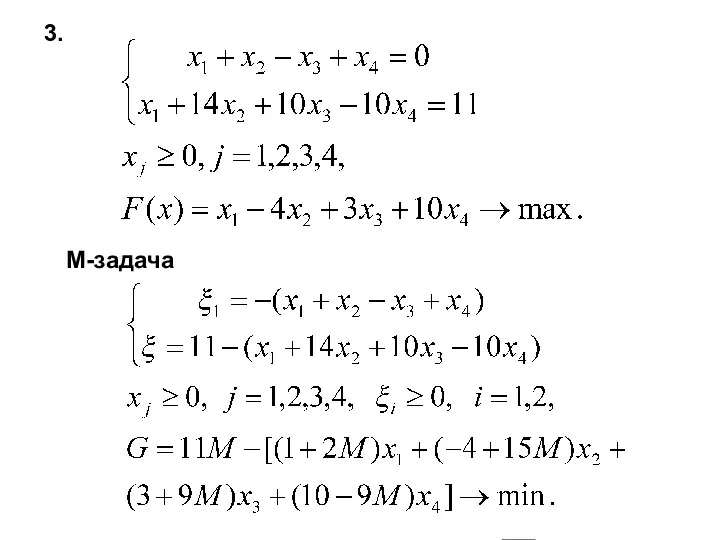








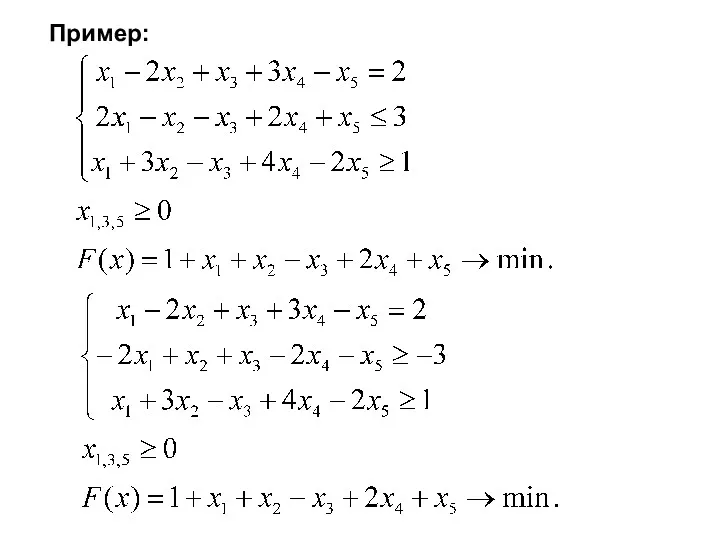
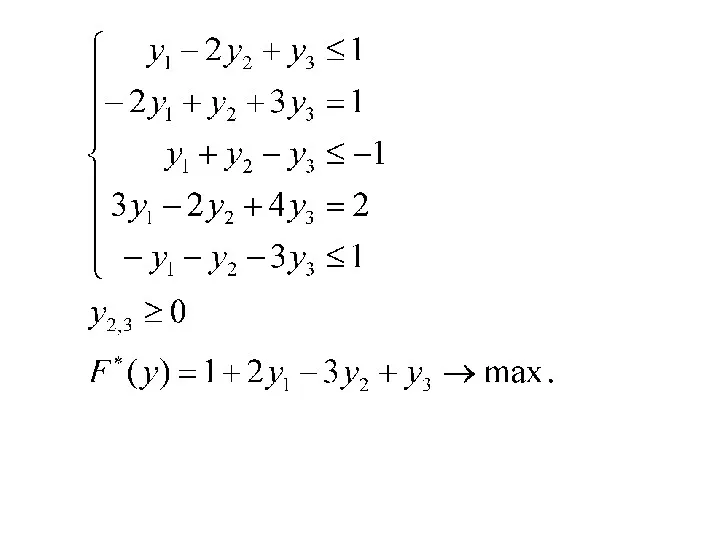

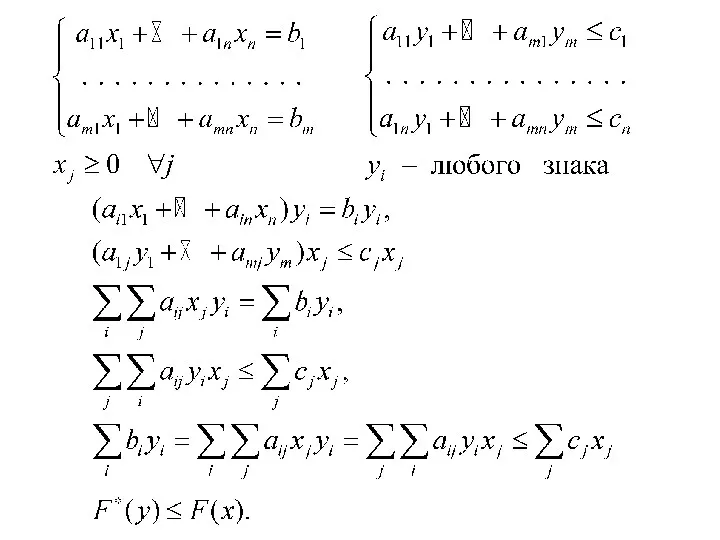


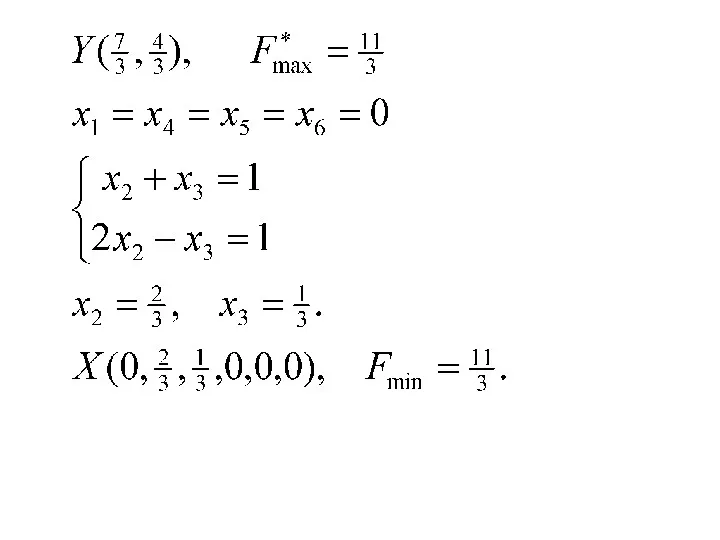


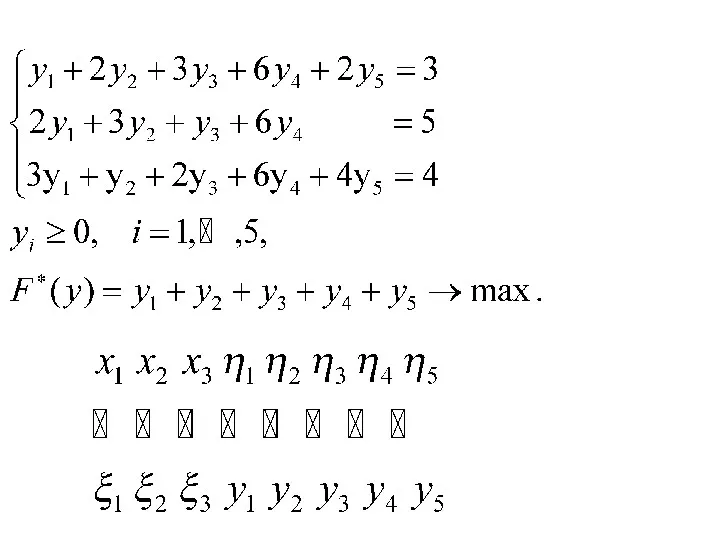

 Финансовое планирование
Финансовое планирование Интерактивная экскурсия Пирамиды Гизы (Египетские пирамиды)
Интерактивная экскурсия Пирамиды Гизы (Египетские пирамиды) Взаимодействие семьи и школы (презентация)
Взаимодействие семьи и школы (презентация)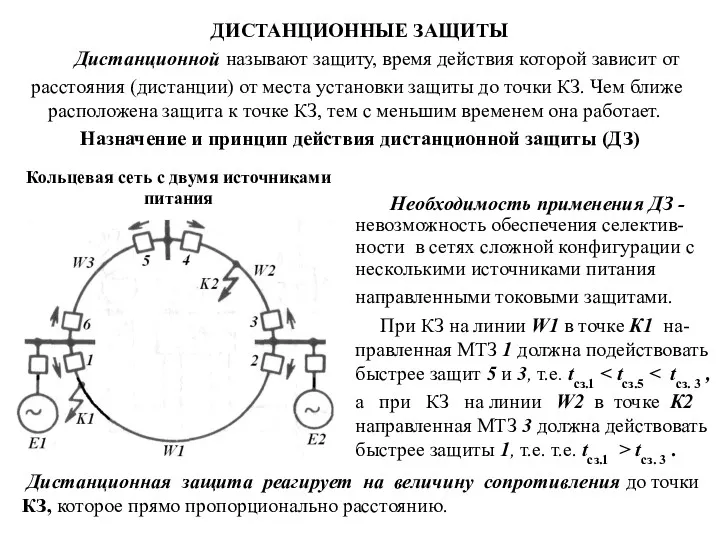 Дистанционные защиты
Дистанционные защиты Послание к Ефесянам
Послание к Ефесянам Презентация. Организация ситуации успеха в учебно - воспитательном процессе.
Презентация. Организация ситуации успеха в учебно - воспитательном процессе.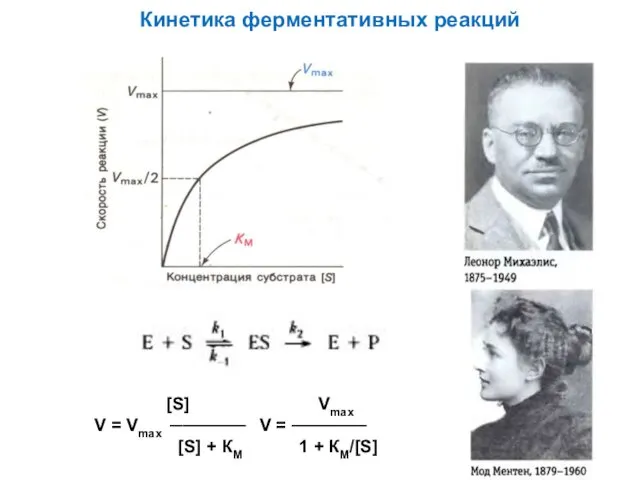 Кинетика ферментативных реакций
Кинетика ферментативных реакций Моделирование фотоэлектрических характеристик твердотельных фотоприемников
Моделирование фотоэлектрических характеристик твердотельных фотоприемников Николай Рубцов
Николай Рубцов Neural Networks
Neural Networks Новая линейка дебетовых карт для зарплатных клиентов
Новая линейка дебетовых карт для зарплатных клиентов Онкология. Отличия доброкачественных опухолей от злокачественных
Онкология. Отличия доброкачественных опухолей от злокачественных 20230329_dlya_izucheniya_v_penii_1
20230329_dlya_izucheniya_v_penii_1 Внеклассное мероприятие Звёздный час
Внеклассное мероприятие Звёздный час Көру мүшелерінің құрылысы. Көрудің маңызы. Көру қызметінің бұзылуы. Көру гигиенасы
Көру мүшелерінің құрылысы. Көрудің маңызы. Көру қызметінің бұзылуы. Көру гигиенасы ЛПД с pin-структурой
ЛПД с pin-структурой Obuchenie_KTs_i_TsI
Obuchenie_KTs_i_TsI Строение и классификация плодов
Строение и классификация плодов Александрийский маяк
Александрийский маяк Составляющие и функции операционной системы Linux
Составляющие и функции операционной системы Linux Сако-скифская цивилизация
Сако-скифская цивилизация Конспект урока по технологии 2 класс Я- парикмахер
Конспект урока по технологии 2 класс Я- парикмахер Государственный строй стран мира
Государственный строй стран мира Презентация Детство, опаленное войной
Презентация Детство, опаленное войной Классификация сталей. Термическая обработка сталей
Классификация сталей. Термическая обработка сталей Адаптируем технологии сами.
Адаптируем технологии сами. Физические свойства нефти и газа
Физические свойства нефти и газа Основные свойства кристаллов
Основные свойства кристаллов