Слайд 2

1.1. Многочлены
Выражение вида:
называется многочленом степени n одного аргумента (переменной).
Будем обозначать многочлен одной
переменной через
, , …
Слайд 3

Степенью многочлена называется наивысшая степень аргумента многочлена.
Для указания степени многочлена
будем использовать нижний индекс заглавной буквы: .
Слайд 4

Запись
представляет собой стандартный вид многочлена одной переменной х степени n,
где
– коэффициенты
степеней переменной х.
Слайд 5

Определение 1.
Два многочлена
и ,
называются равными,
если их коэффициенты
при соответствующих степенях
х равны,
Слайд 6
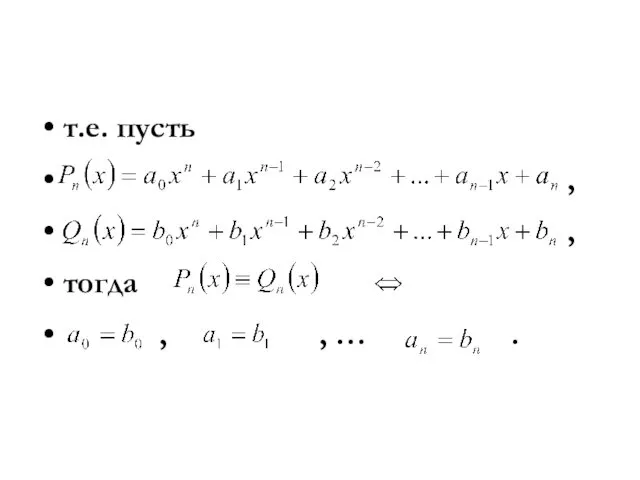
т.е. пусть
,
,
тогда
, , … .
Слайд 7

Многочлен
называется многочленом степени
выше чем многочлен ,
если наивысший показатель
степени х многочлена
больше наивысшего показателя степени х многочлена
т. е.
Слайд 8

Многочлены
и
называются многочленами одинаковой степени, если
.
Слайд 9

Основные формулы сокращенного умножения:
;
;
;
;
;
;
;
Слайд 10

1.2. Деление многочлена на многочлен
Любой многочлен может быть представлен в виде:
,
где
– делитель многочлена ,
– частное от деления многочлена
на многочлен ,
Слайд 11

– остаток от деления многочлена
на многочлен .
Причем, сумма
степеней делителя и частного равна степени делимого,
т. е. ,
степень остатка меньше степени делителя.
Слайд 12

Определение 1.
Многочлен
делится на многочлен ,
если остаток от деления
равен нулю,
т.е. .
Слайд 13

Пример 1.
Найти частное и остаток от деления многочлена
на
.
Слайд 14

Деление столбиком.
x4 + 3x3 - 5x2 + 6x – 1 -x2 +
3x + 2
x4 - 3x3 - 2x2 - x2 - 6 x - 15 = G2(х)
6x3 - 3x2 + 6x
6x3 -18x2 - 12x
15x2 + 18x - 1
15x2 - 45x - 30
63 x + 29 = R(x)
Слайд 15

1.3. Деление многочлена на двучлен
Слайд 16

Теорема Безу
При делении многочлена
на двучлен
остаток от деления равен значению
многочлена при ,
т. е. .
Слайд 17

Доказательство.
Пусть при делении многочлена
на двучлен
имеем
.
Слайд 18

Подставим в полученное выражение значение ,
получим ,
или ,
или ,
что
и требовалось доказать.
Слайд 19

Определение 1.
Корнем многочлена называется такое значение аргумента, при котором значение многочлена
обращается в нуль.
Слайд 20

Таким образом,
является корнем многочлена ,
если .
Слайд 21

Следствия из теоремы Безу
Слайд 22

1.
Многочлен
делится на двучлен
тогда и только тогда, когда число α
является корнем многочлена .
Слайд 23

Другими словами,
если при делении многочлена
на двучлен
остаток R(x)
от деления равен нулю,
то значение
– корень многочлена.
Слайд 24

Доказательство.
По теореме Безу ,
если ,
то следовательно .
По определению корня
многочлена имеем, что
– корень многочлена, что и требовалось доказать.
Слайд 25

Слайд 26

Слайд 27

Слайд 28

Слайд 29

Слайд 30

Слайд 31

Слайд 32

Слайд 33

Слайд 34

Слайд 35

Слайд 36

Слайд 37

Слайд 38

Слайд 39

Слайд 40

Слайд 41

Слайд 42

Слайд 43

1. 4. Корни многочлена. Теорема о корнях многочлена.
Слайд 44





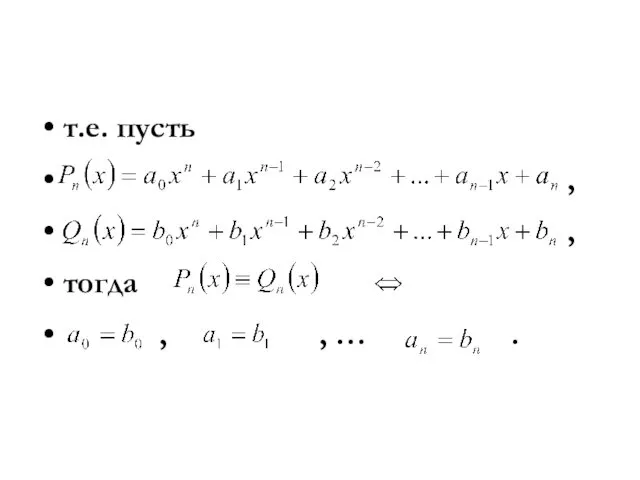






































 Телевизоры TCL
Телевизоры TCL 20231019_proizvedenie_vektora_na_chislo
20231019_proizvedenie_vektora_na_chislo Компьютерная игра как современное средство подготовки ребенка к школе
Компьютерная игра как современное средство подготовки ребенка к школе Food and fertilizers. Outline
Food and fertilizers. Outline Современные средства поражения и их поражающие факторы. Ядерное оружие и его боевые свойства
Современные средства поражения и их поражающие факторы. Ядерное оружие и его боевые свойства Цукерки. Технологія виготовлення
Цукерки. Технологія виготовлення Роль биологии в формировании современной научной картины мира, практическое значение биологических знаний
Роль биологии в формировании современной научной картины мира, практическое значение биологических знаний Новогодняя викторина
Новогодняя викторина Перелетные птицы
Перелетные птицы Религиозные объединения и организации в Российской Федерации
Религиозные объединения и организации в Российской Федерации Оптичне й лазерне випромінювання. Оптичні властивості тканин організму
Оптичне й лазерне випромінювання. Оптичні властивості тканин організму Фонд содействия гражданскому обществу Республики Башкортостан. Конкурс грантов главы РБ для НКО
Фонд содействия гражданскому обществу Республики Башкортостан. Конкурс грантов главы РБ для НКО Основные положения тектоники литосферных плит
Основные положения тектоники литосферных плит Предистория науки. Преднаука
Предистория науки. Преднаука Защита информации от несанкционированного доступа. Лекция 1
Защита информации от несанкционированного доступа. Лекция 1 Тағамдық концентраттардың класификациясы,тұтынушылық қасиеттері
Тағамдық концентраттардың класификациясы,тұтынушылық қасиеттері Правила приема в 2021 году
Правила приема в 2021 году Анимированный кроссворд Первоначальные химические понятия
Анимированный кроссворд Первоначальные химические понятия Кто хочет стать миллионером. Игра для учеников 7 класса
Кто хочет стать миллионером. Игра для учеников 7 класса Document Object Model (объектная модель документа). Browser Object Model (объектная модель браузера)
Document Object Model (объектная модель документа). Browser Object Model (объектная модель браузера) Архитектура компьютера. Виды памяти
Архитектура компьютера. Виды памяти Презентация к открытому уроку
Презентация к открытому уроку Я и моя семья. 1 класс
Я и моя семья. 1 класс Отборочный тур муниципальной игры Юный пешеход – друг дорог!
Отборочный тур муниципальной игры Юный пешеход – друг дорог! Родительское собрание на тему Воспитание самостоятельности
Родительское собрание на тему Воспитание самостоятельности Познавательное пособие История гитары
Познавательное пособие История гитары Лучистый теплообмен. Основные свойства и характеристики. Законы лучистого теплообмена. (Занятие 11)
Лучистый теплообмен. Основные свойства и характеристики. Законы лучистого теплообмена. (Занятие 11) Философия, ее роль в культуре человечества
Философия, ее роль в культуре человечества