Содержание
- 2. Модели в нашей жизни
- 3. Что такое модель? Модель – это объект, который обладает некоторыми свойствами другого объекта (оригинала) и используется
- 4. Что можно моделировать? Модели объектов: уменьшенные копии зданий, кораблей, самолетов, … модели ядра атома, кристаллических решеток
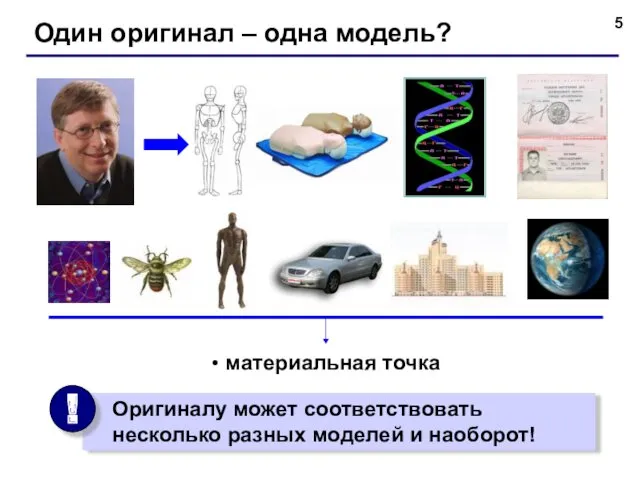
- 5. Один оригинал – одна модель? материальная точка
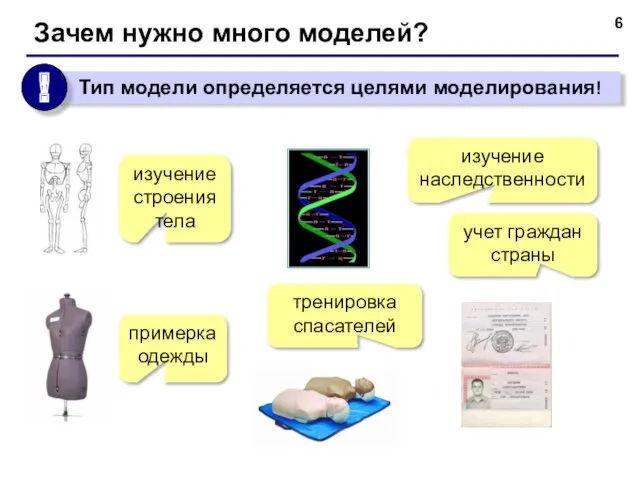
- 6. Зачем нужно много моделей? изучение строения тела примерка одежды изучение наследственности тренировка спасателей учет граждан страны
- 7. Природа моделей материальные (физические, предметные) модели: информационные модели представляют собой информацию о свойствах и состоянии объекта,
- 8. Модели по области применения учебные (в т.ч. тренажеры) опытные – при создании новых технических средств научно-технические
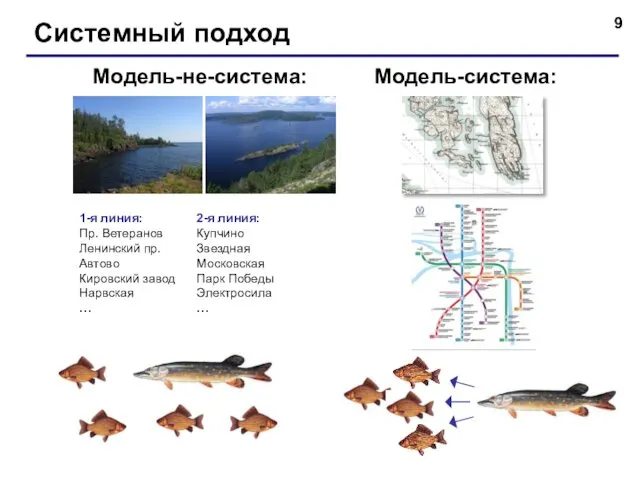
- 9. Системный подход Модель-система: Модель-не-система: 1-я линия: Пр. Ветеранов Ленинский пр. Автово Кировский завод Нарвская … 2-я
- 10. V. Проверка практикой, анализ результатов Возможные выводы: задача решена, модель адекватна необходимо изменить алгоритм или условия
- 11. Пример. Задача. Обезьяна хочет сбить бананы на пальме. Как ей надо кинуть кокос, чтобы попасть им
- 12. I. Постановка задачи Допущения: кокос и банан считаем материальными точками расстояние до пальмы известно рост обезьяны
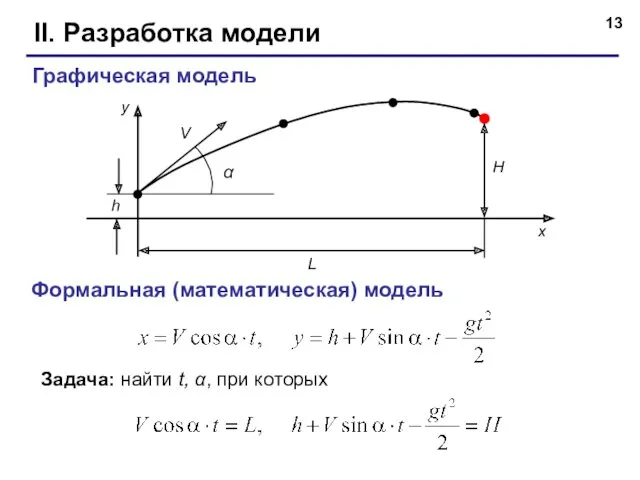
- 13. II. Разработка модели Графическая модель h Формальная (математическая) модель Задача: найти t, α, при которых
- 14. III. Тестирование модели при нулевой скорости кокос падает вертикально вниз при t=0 координаты равны (0,h) при
- 15. IV. Эксперимент Метод I. Меняем угол α. Для выбранного угла α строим траекторию полета ореха. Если
- 16. V. Анализ результатов Всегда ли обезьяна может сбить банан? Что изменится, если обезьяна может бросать кокос
- 17. Модели и моделирование © К.Ю. Поляков, 2007-2011 Тема 3. Модели биологических систем (по мотивам учебника А.Г.
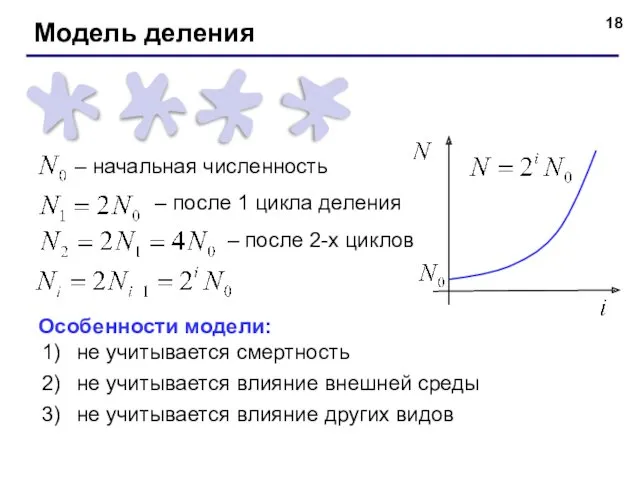
- 18. – начальная численность – после 1 цикла деления – после 2-х циклов Особенности модели: не учитывается
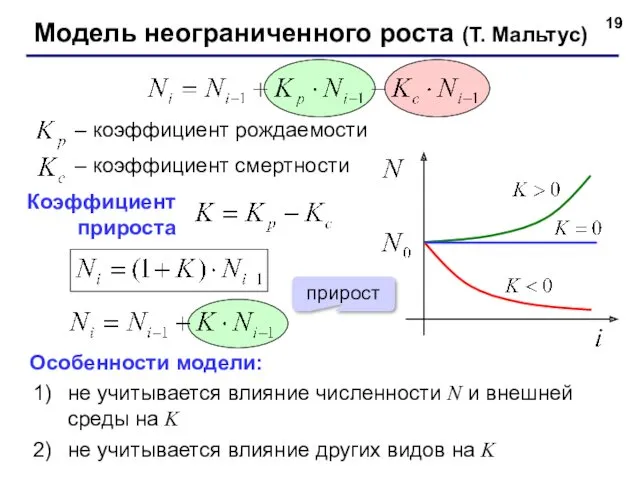
- 19. – коэффициент рождаемости – коэффициент смертности Особенности модели: не учитывается влияние численности N и внешней среды
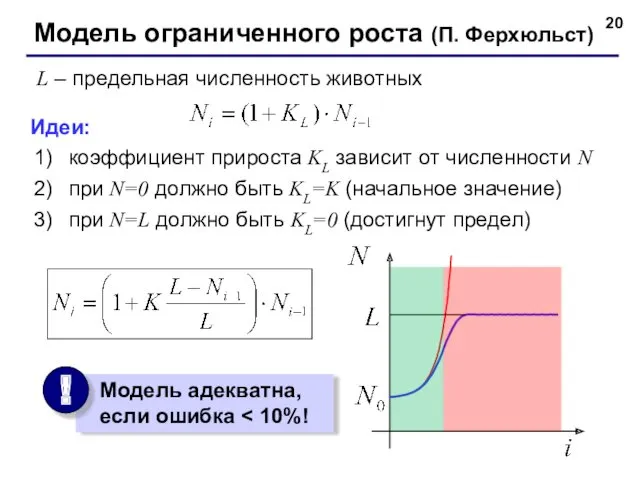
- 20. Модель ограниченного роста (П. Ферхюльст) L – предельная численность животных Идеи: коэффициент прироста KL зависит от
- 21. Модель с отловом Примеры: рыбоводческое хозяйство, разведение пушных зверей и т.п.
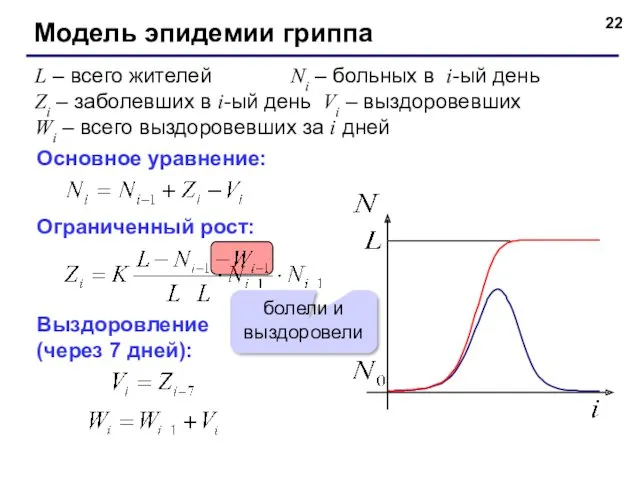
- 22. Модель эпидемии гриппа L – всего жителей Ni – больных в i-ый день Zi – заболевших
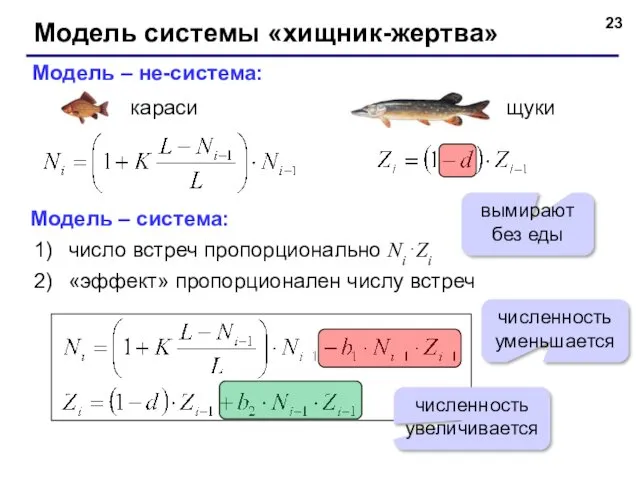
- 23. Модель системы «хищник-жертва» Модель – не-система: Модель – система: число встреч пропорционально Ni⋅Zi «эффект» пропорционален числу
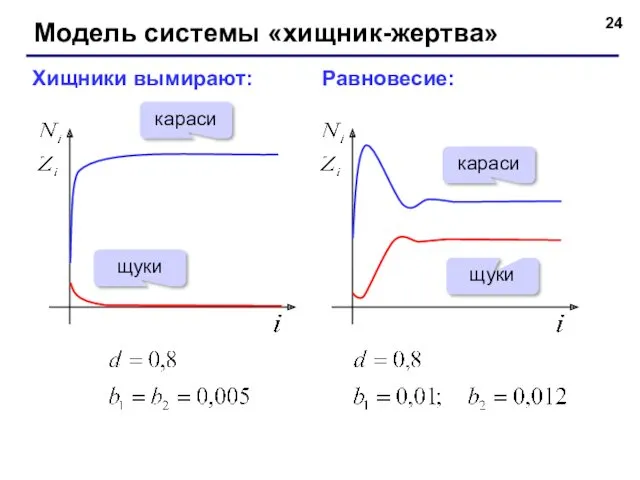
- 24. Модель системы «хищник-жертва» Хищники вымирают: Равновесие: караси щуки караси щуки
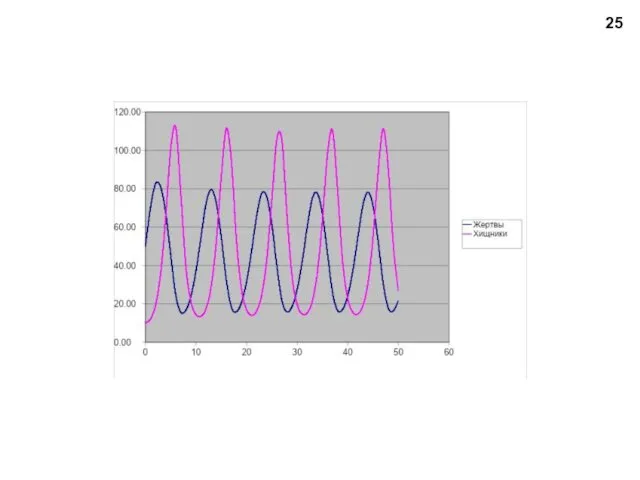
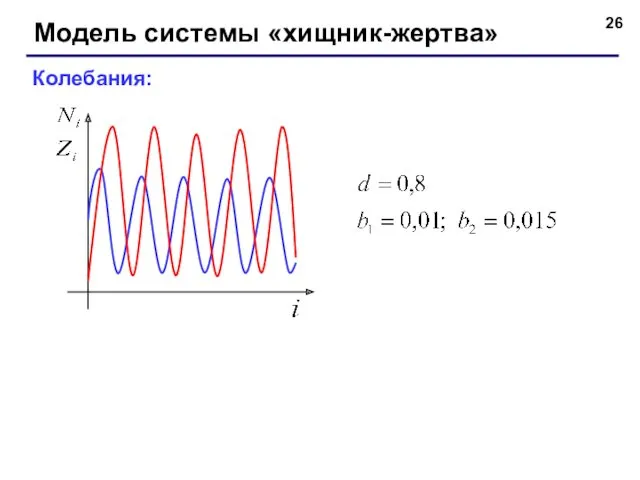
- 26. Модель системы «хищник-жертва» Колебания:
- 28. Скачать презентацию













 Основы педагогического мастерства и Формирование информационной компетентности участников образовательного процесса
Основы педагогического мастерства и Формирование информационной компетентности участников образовательного процесса Coca-Cola Format Template
Coca-Cola Format Template Учимся жить дружно
Учимся жить дружно Приемы устного счета
Приемы устного счета Тиристоры
Тиристоры Биогаз - экологически чистое топливо
Биогаз - экологически чистое топливо Районный семинар школьных библиотекарей
Районный семинар школьных библиотекарей Уголовная ответственность несовершеннолетних
Уголовная ответственность несовершеннолетних Виртуальная экскурсия на Соколовую гору г.Саратова
Виртуальная экскурсия на Соколовую гору г.Саратова Татар теле 4 класс
Татар теле 4 класс Процессы в неживой природе. 6 класс
Процессы в неживой природе. 6 класс МАИ – ведущий аэрокосмический вуз России
МАИ – ведущий аэрокосмический вуз России Паспорт мини-музея Хлеба
Паспорт мини-музея Хлеба Работа с одарёнными детьми
Работа с одарёнными детьми Обеспечение и поддержание инфекционной безопасности при выполнении трудовых действий
Обеспечение и поддержание инфекционной безопасности при выполнении трудовых действий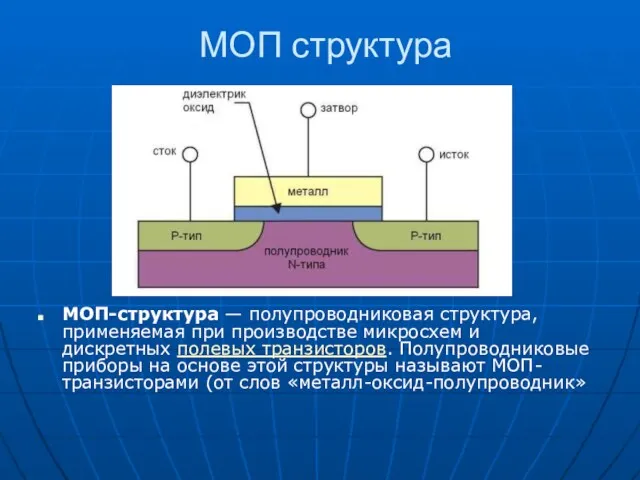 МОП и КМОП структуры
МОП и КМОП структуры Профессиональный стресс. Проявление хронической усталости и психического выгорания
Профессиональный стресс. Проявление хронической усталости и психического выгорания Моя семья
Моя семья Калібрування аналогових вольтметрів (тема № 2, заняття № 1)
Калібрування аналогових вольтметрів (тема № 2, заняття № 1) Симптомы и методы обследования в пульмонологии
Симптомы и методы обследования в пульмонологии Проблемы реализации принципа презумпции невиновности на досудебных стадиях
Проблемы реализации принципа презумпции невиновности на досудебных стадиях Урок развития речи в 6 классе
Урок развития речи в 6 классе Устройство компьютера
Устройство компьютера Здоровый образ жизни
Здоровый образ жизни Как заставить себя учиться
Как заставить себя учиться Основные составляющие шрифта
Основные составляющие шрифта The Martian
The Martian Препроцессор. Роль препроцессора при компиляции программы
Препроцессор. Роль препроцессора при компиляции программы