Содержание
- 2. 1. Фиктивные объясняющие переменные До сих пор рассматривались модели, в которых в качестве объясняющих переменных выступали
- 3. Примерами таких признаков могут слу-жить: образование (начальное, среднее, выс-шее), пол человека (мужской, женский) и т.д. Чтобы
- 4. Такие переменные приводят к скачкооб-разному изменению параметров регрессион-ных моделей и в этом случае говорят об ис-следовании
- 5. где , если й персоналий не имеет высшего образования и в противном случае. Нетрудно видеть, что
- 6. Такие модели называют ANCOVA-моделями (модели ковариационного анализа). Обычно в качестве фиктивных перемен-ных выступают бинарные переменные, т.е.
- 7. где , если служащий является муж-чиной, и , если служащий явля-ется женщиной, количественные приз-наки (стаж работы,
- 8. Если рассматриваемый качественный признак имеет более чем два уровня, напри-мер, их число равно , то в
- 9. В данной модели
- 10. Как видим, третьей фиктивной переменной не требуется, так как при = =0 следует, что служащий имеет
- 11. 2. Модели с дискретными зависимыми переменными Нередко зависимая переменная по своей природе является дискретной, например, если
- 12. Номинальные переменные. Рассмотрим следующие примеры. 1. Семейное положение мужчины можно выразить следующими категориями: холост, женат, разведен,
- 13. Выбор значения осуществляется из двух или более альтернатив. Если имеется только две возможности, то наблюдения обычно
- 14. Главная особенность приведённых при-меров состоит в том, что имеющиеся альтер-нативы нельзя естественным образом упорядочить, их нумерация
- 15. 1. Доход семьи: низкий, средний, высокий, очень высокий. 2. Уровень образования: начальное, незакон-ченное среднее, среднее, незаконченное
- 16. Количественные целочисленные переменные. Примерами таких переменных служат: 1. Число предприятий страны, обанкро-тившихся в текущем году. 2.
- 17. Для моделей с описанными дискретными зависимыми переменными возможно форма-льное применение МНК для оценки их коэф-фициентов. Однако
- 18. Если зависимая переменная является номинальной и количество альтернатив бо-лее двух, то результаты оценивания МНК вообще теряют
- 19. Рассмотрим вначале простейшие модели бинарного выбора, когда результирующий показатель может принимать только два значения: 0 и
- 20. На решение о покупке автомобиля влияют различные факторы: доход семьи, количес-тво членов семьи, их возраст, место
- 21. Выдвигая различные предположения о характере зависимости переменной от вектора и случайного фактора , можно получить различные
- 22. Поскольку , как случайная величина, принимает только два значения ( 0 и 1), а по предпосылке
- 23. В итоге модель (2) может быть записана в следующем виде и поэтому её называют линейной моделью
- 24. может находиться вне отрезка , что не поддается разумной интерпретации, поско-льку левая часть уравнения (3) представ-ляет
- 25. От указанного недостатка, связанного с предположением о линейной зависимости вероятности от вектора , можно избавиться, если
- 26. В частности, в качестве можно взять функцию распределения вероятностей не-которой случайной величины. Наиболее распространенными функци-ями такого
- 27. 2. Если в качестве выбирают логисти-ческую функцию то говорят о logit-модели. Для оценивания коэффициентов probit- и
- 28. В том случае, когда номинальная зависимая переменная имеет более двух альтернатив, т.е. требуется построить модель множест-венного
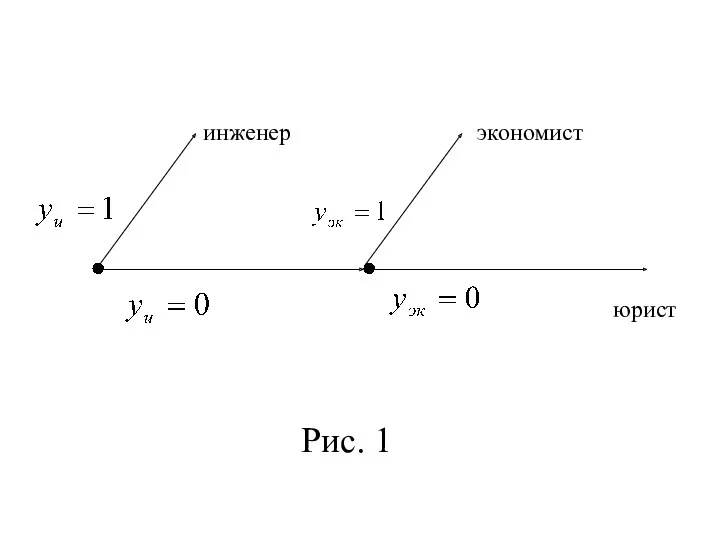
- 29. Тогда выбор одного из трёх вариантов про-фессий можно описать в виде графа после-довательных действий, в вершинах
- 30. Рис. 1
- 31. 3. Тесты Гуйарати и Чоу Пусть требуется оценить парную регрессию, в которой в качестве объясняющей переменной
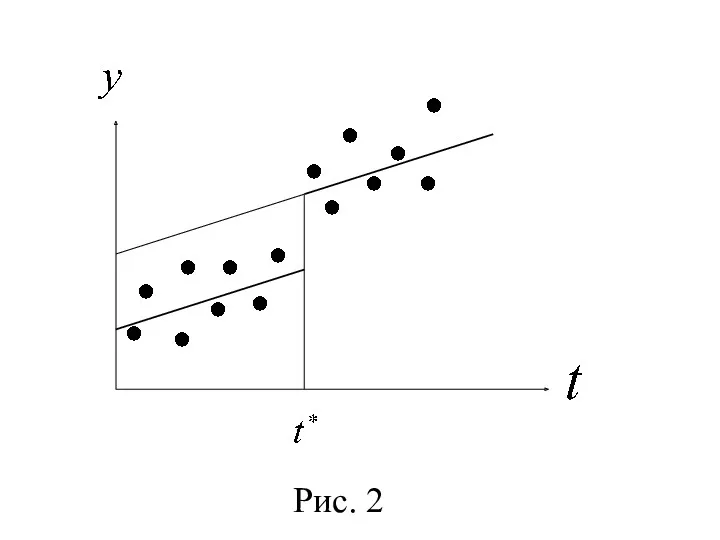
- 32. Пусть до момента было произведено наблюдений показателя , а после этого момента - . В итоге
- 33. Если же структурные изменения незна-чительно повлияли на характер динамики , то её описывают единым по всей
- 34. где В итоге для каждого промежутка времени получаются следующие оценки уравнения регрессии: для : ; для
- 35. С помощью критерия Стьюдента проверяют значимость полученных оценок коэффициентов регрессии (5). Здесь возможны следующие случаи. 1°.
- 36. Рис. 2
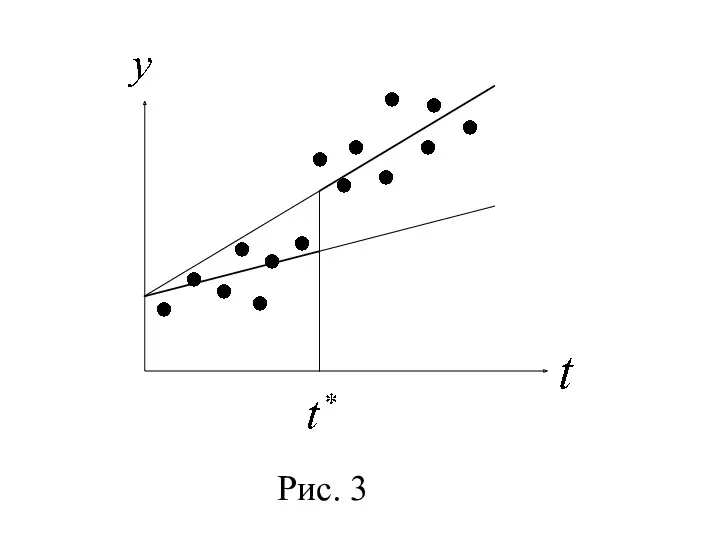
- 37. Рис. 3
- 38. 2°. Если параметр статистически значим, а не является значимым, то различаются коэффициенты регрессии кусочно-линейной модели (рис.
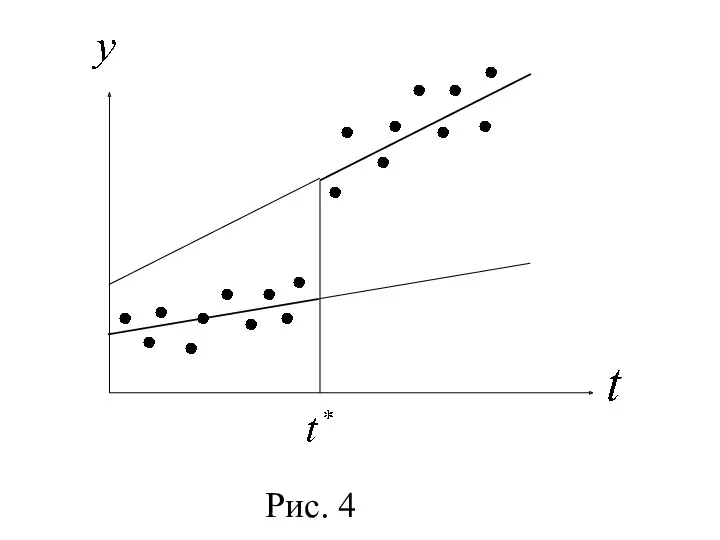
- 39. Рис. 4
- 40. 4°. Если оба параметра и статистически незначимы, то используется единая по всей совокупности данных линейная регрессия,
- 41. Выдвигается гипотеза о незначительном влиянии структурных изменений в экономи-ке. Согласно тесту Чоу гипотеза отвер-гается на уровне
- 42. больше , найденного по таблицам по заданному уровню значимости и числу степеней свободы В формуле (6)
- 44. Скачать презентацию





































 Arduino. Что это такое?
Arduino. Что это такое? Моё хобби
Моё хобби Хочу стать палеонтологом
Хочу стать палеонтологом Работа над ошибками в комплексной работе 3 класс.Осень в лесу.(И.Соколов –Микитов )
Работа над ошибками в комплексной работе 3 класс.Осень в лесу.(И.Соколов –Микитов ) Аппликация Собачка из кругов
Аппликация Собачка из кругов Закрепляем звук [л]
Закрепляем звук [л] Обобщение сведений о классах соединений
Обобщение сведений о классах соединений Методика развития речи как педагогическая наука
Методика развития речи как педагогическая наука Культура Беларуси
Культура Беларуси Сайт Strahovka59.ru
Сайт Strahovka59.ru Использование техники оригами во внеурочной деятельности как средство развития конструкторских умений учащихся
Использование техники оригами во внеурочной деятельности как средство развития конструкторских умений учащихся Пневмонии у детей
Пневмонии у детей Основы микробиологии и иммунологии
Основы микробиологии и иммунологии Чрезвычайные ситуации химического характера
Чрезвычайные ситуации химического характера Алтай - уникальный природный район Восточной Сибири
Алтай - уникальный природный район Восточной Сибири Кинезиологические упражнения как средство помощи детям с проблемами в развитии
Кинезиологические упражнения как средство помощи детям с проблемами в развитии Гепард. Места обитания. Основная причина вымирания
Гепард. Места обитания. Основная причина вымирания Система управления безопасностью полетов эксплуатанта. Управление факторами риска
Система управления безопасностью полетов эксплуатанта. Управление факторами риска культура профессионального общения педагога
культура профессионального общения педагога Презентация Работа с жанром притча как один способов формирования УУД на уроках ОРКСЭ
Презентация Работа с жанром притча как один способов формирования УУД на уроках ОРКСЭ Портфолио учителя начальных классов
Портфолио учителя начальных классов презентация Мин яратам, сине Татарстан
презентация Мин яратам, сине Татарстан Песенки -потешки в режиме дня для детей младшей группы
Песенки -потешки в режиме дня для детей младшей группы Предложения с однокоренными словами
Предложения с однокоренными словами кроме 4, 75, 76ASEPTIKA_I_ANTISEPTIKA
кроме 4, 75, 76ASEPTIKA_I_ANTISEPTIKA Моделирование химико-технологических процессов
Моделирование химико-технологических процессов Биологические основы паразитизма и трансмиссивных заболеваний
Биологические основы паразитизма и трансмиссивных заболеваний Германия в конце XIX – начале XX века. Борьба за место под солнцем
Германия в конце XIX – начале XX века. Борьба за место под солнцем