Содержание
- 2. Функция F(x)называется первообразной для функции f(x)на некотором промежутке, если для всех x из этого промежутка
- 3. Показать, что функция является первообразной для функции Решение:
- 4. Показать, что функция является первообразной для функции Решение:
- 5. Если F(x)– первообразная для функции f(x) на некотором промежутке, то функция F(x)+C также является первообразной функции
- 11. Правила нахождения первообразных
- 12. Если F(x)– первообразная для функции f(x), а G(x)– первообразная для функции g(x), то F(x)+G(x)– первообразная для
- 13. Если F(x)– первообразная для функции f(x), а а –константа, то аF(x)– первообразная для функции аf(x) Постоянный
- 14. Если F(x) – первообразная для функции f(x), а k и b- константы, причем то -первообразная для
- 16. Скачать презентацию




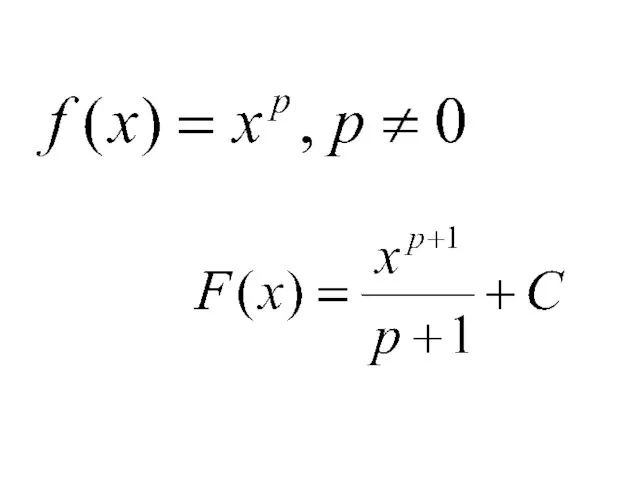
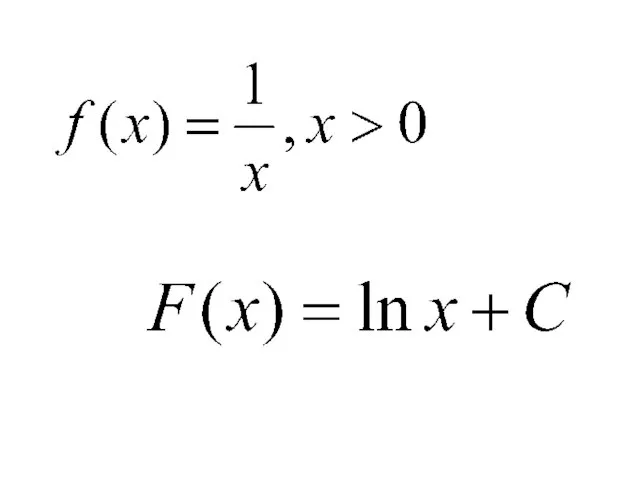
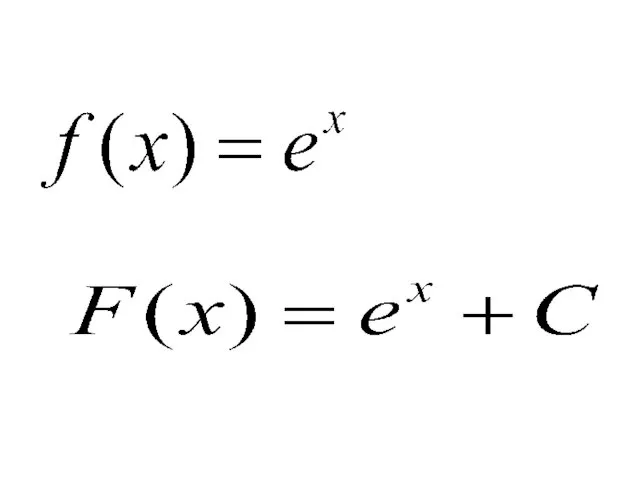
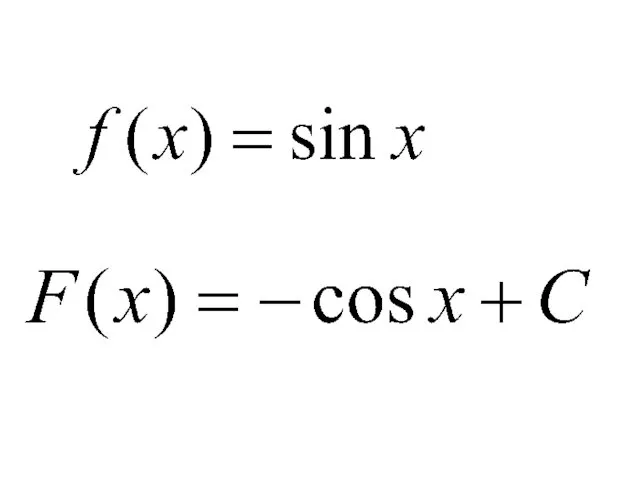
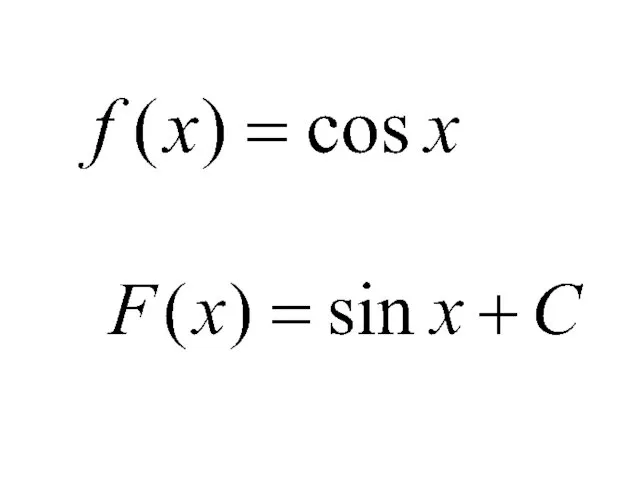




 Профессия - техник. Техническая эксплуатация и обслуживание электрического и электромеханического оборудования
Профессия - техник. Техническая эксплуатация и обслуживание электрического и электромеханического оборудования История книги.
История книги. Уральські гори
Уральські гори Тематическая беседа с родителями на тему Как понять подростка
Тематическая беседа с родителями на тему Как понять подростка Наследственные болезни человека, их причины и профилактика
Наследственные болезни человека, их причины и профилактика Проект по географии 7 класс Остров Робинзона Крузо: миф или реальность
Проект по географии 7 класс Остров Робинзона Крузо: миф или реальность Информация для родителей. Критические периоды в развитии речевой функции у детей.
Информация для родителей. Критические периоды в развитии речевой функции у детей. Техническое обслуживание и ремонт автомобильного транспорта
Техническое обслуживание и ремонт автомобильного транспорта Важнейшее христианское таинство - крещение
Важнейшее христианское таинство - крещение Концепция экологического менеджмента. Система экологического менеджмента. Требования к системе экологического менеджмента
Концепция экологического менеджмента. Система экологического менеджмента. Требования к системе экологического менеджмента презентация исследовательской работы по географии Миграции в МБОУ Северская СОШ
презентация исследовательской работы по географии Миграции в МБОУ Северская СОШ Экономика родного края. Тульская область
Экономика родного края. Тульская область Социальный проект Равные права - равные возможности
Социальный проект Равные права - равные возможности Макроэкономические показатели. (Лекция 6)
Макроэкономические показатели. (Лекция 6) Тема 2. AD-AS
Тема 2. AD-AS Окончание и основа. 2 класс
Окончание и основа. 2 класс Стойкость и защита древесины
Стойкость и защита древесины Как развивалась жизнь на земле презентация по природоведению для 5 класса по программе Сонина
Как развивалась жизнь на земле презентация по природоведению для 5 класса по программе Сонина Урок обобщения и систематизации знаний по теме: Важнейшие классы неорганических соединений.
Урок обобщения и систематизации знаний по теме: Важнейшие классы неорганических соединений. Презентация к уроку технологии Двухтрубный пароход (оригами)
Презентация к уроку технологии Двухтрубный пароход (оригами) Подходы в определении видов профессиональной деятельности и анализ потребности в умениях
Подходы в определении видов профессиональной деятельности и анализ потребности в умениях Внеклассное мероприятие В гостях у сказки
Внеклассное мероприятие В гостях у сказки Викторина по английскому языку, 6 класс
Викторина по английскому языку, 6 класс Інформація та інформаційні процеси
Інформація та інформаційні процеси Семейные праздники
Семейные праздники Армии и войны русского феодального общества
Армии и войны русского феодального общества Группы крови АВ0 и резус. Принадлежность крови
Группы крови АВ0 и резус. Принадлежность крови Деформации и напряжения при сварке
Деформации и напряжения при сварке