Разработка модели и исследование напряженно-деформированного состояния стеклопластика на основе термопластичной матрицы презентация
Содержание
- 2. Структура ВКРМ: Введение 1. Дефекты и их влияние на физико-механические характеристики в ПКМ 2. Моделирование деформационно-прочностных
- 3. Раздел 1. Дефекты и их влияние на физико-механические характеристики в ПКМ 1.1 Литературный обзор Схема основных
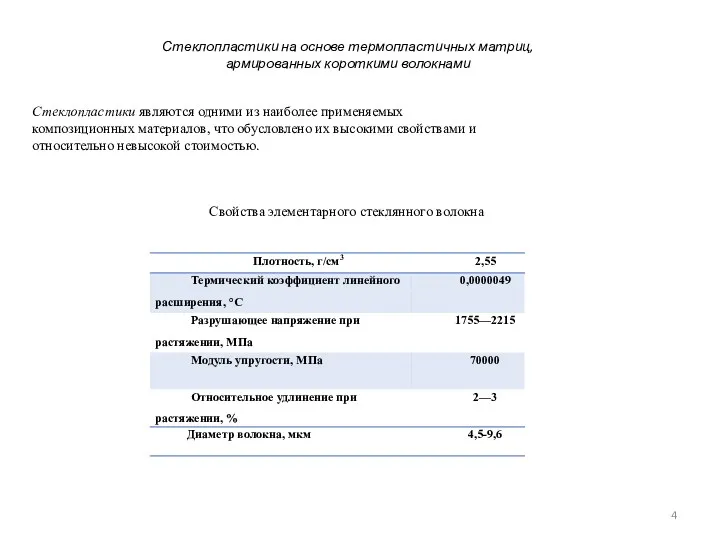
- 4. Стеклопластики на основе термопластичных матриц, армированных короткими волокнами Стеклопластики являются одними из наиболее применяемых композиционных материалов,
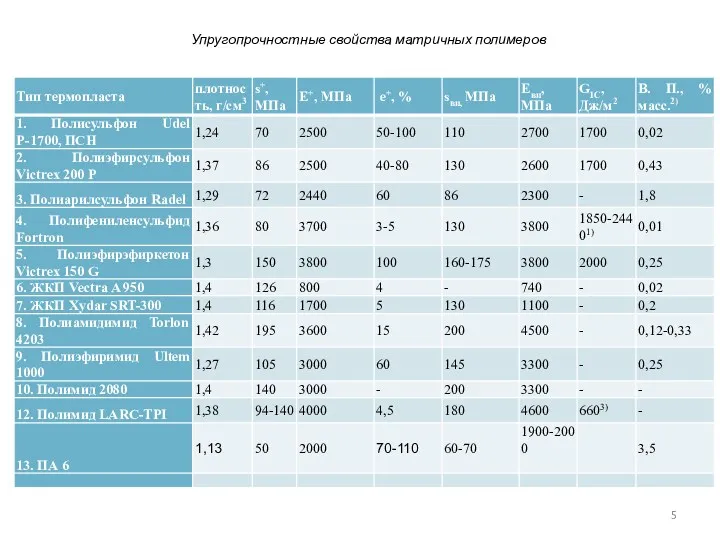
- 5. Упругопрочностные свойства матричных полимеров
- 6. Влияние дефектов на прочностные характеристики ПКМ Ударная прочность стеклонаполненных полиамидов при различных условиях нагружения
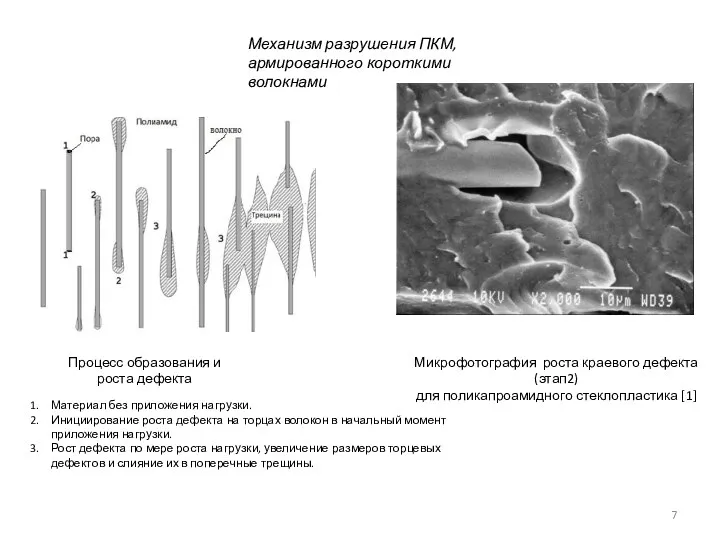
- 7. Механизм разрушения ПКМ, армированного короткими волокнами Процесс образования и роста дефекта Микрофотография роста краевого дефекта (этап2)
- 8. Микроподход в моделировании ПКМ. Блочный метод При применении метода конечных элементов для композитов с учетом указанного
- 9. МОДЕЛИ ПКМ ДЛЯ БЛОЧНОГО МЕТОДА Все блочные модели являются осесимметричными и состоят из цилиндрических блоков матрицы
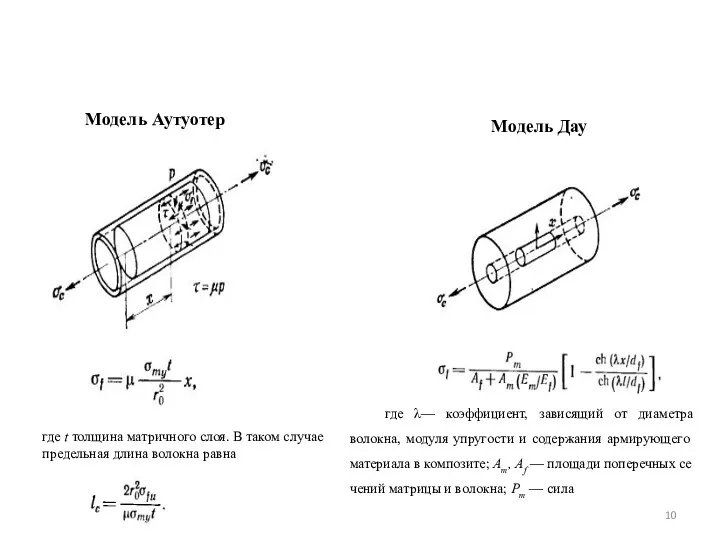
- 10. Модель Аутуотер Модель Дау где t толщина матричного слоя. В таком случае предельная длина волокна равна
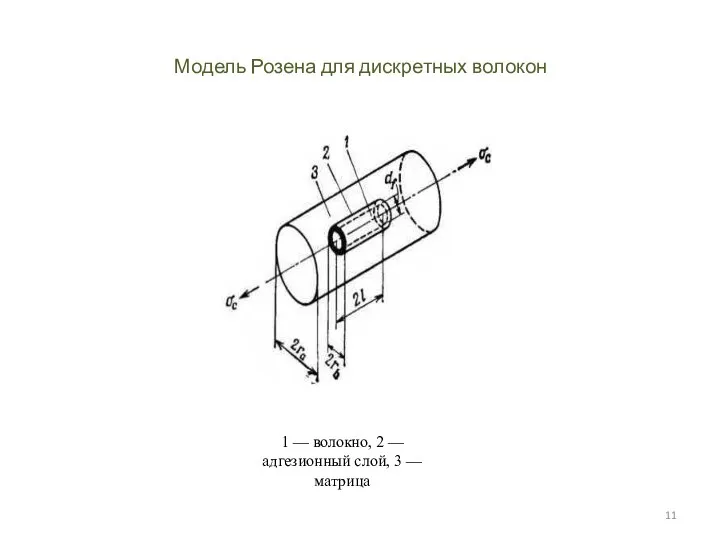
- 11. Модель Розена для дискретных волокон 1 — волокно, 2 — адгезионный слой, 3 — матрица
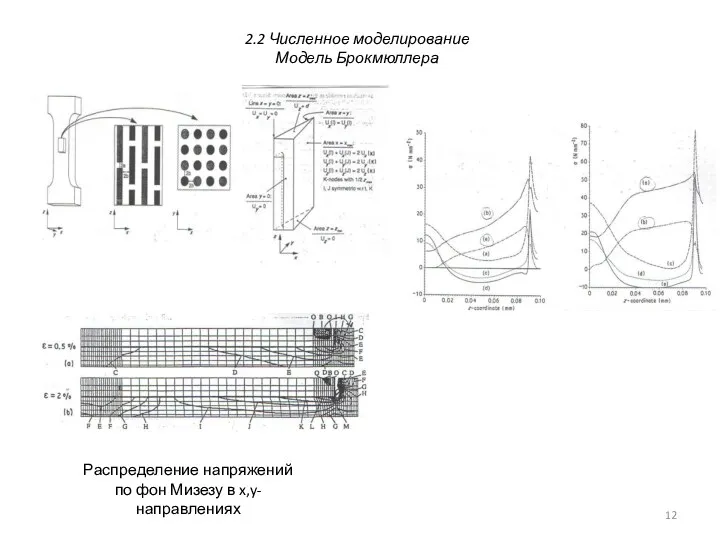
- 12. 2.2 Численное моделирование Модель Брокмюллера Распределение напряжений по фон Мизезу в x,y-направлениях
- 13. Цель работы: Разработка модели и исследование деформационно-прочностных свойств стеклопластика на основе термопластичной матрицы, армированной короткими стеклянными
- 14. Раздел 3. Разработка дискретно-армированных моделей ПКМ с дефектами на границе раздела и исследование деформационно-прочностных свойств 3.1.
- 15. 3.2. Методика построения КЭ модели развития дефекта на границе раздела фаз. Постановка задачи Назначение типов конечных
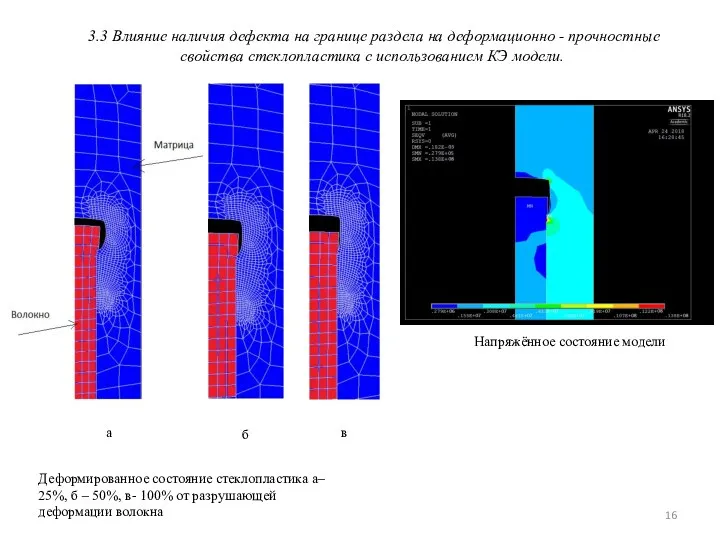
- 16. Напряжённое состояние модели 3.3 Влияние наличия дефекта на границе раздела на деформационно - прочностные свойства стеклопластика
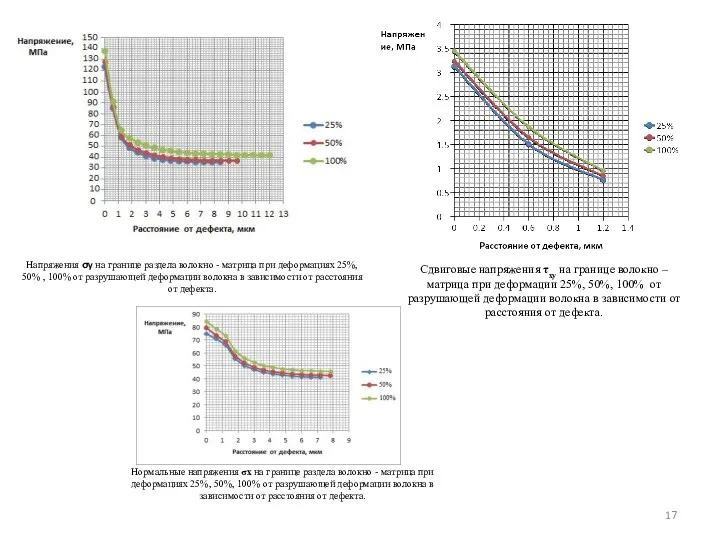
- 17. Напряжения σy на границе раздела волокно - матрица при деформациях 25%, 50% , 100% от разрушающей
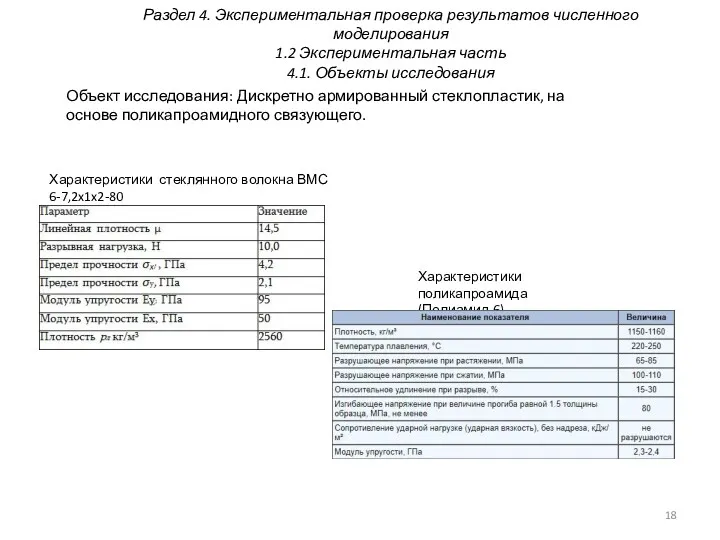
- 18. Раздел 4. Экспериментальная проверка результатов численного моделирования 1.2 Экспериментальная часть 4.1. Объекты исследования Характеристики поликапроамида (Полиамид-6)
- 19. Схема изготовления образца стеклопластика 1.Раскрой тканого полуфабриката ТОПАС и полиамидной плёнки на заготовки. 2. Подготовка формы
- 20. 4.2 Методика испытаний. Определение физико-механических характеристик стеклопластика при растяжении по ГОСТ 25.601-80 Эскиз образца в виде
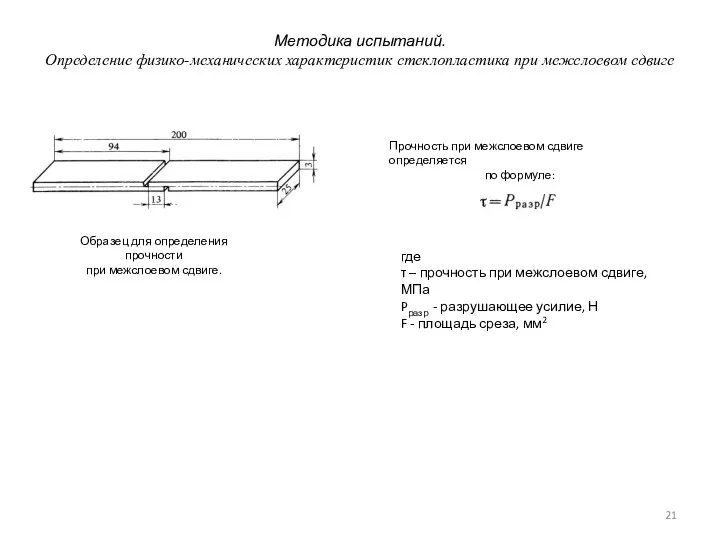
- 21. Методика испытаний. Определение физико-механических характеристик стеклопластика при межслоевом сдвиге Образец для определения прочности при межслоевом сдвиге.
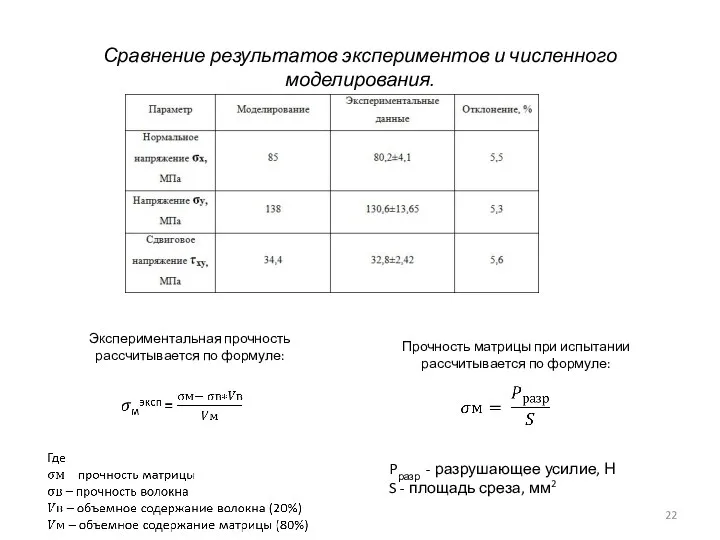
- 22. Сравнение результатов экспериментов и численного моделирования. Экспериментальная прочность рассчитывается по формуле: Прочность матрицы при испытании рассчитывается
- 24. Скачать презентацию










 Дорога в четырнадцать шагов. Рекомендации для родителей.
Дорога в четырнадцать шагов. Рекомендации для родителей. Популяционный уровень жизни
Популяционный уровень жизни Заболевания прямой кишки
Заболевания прямой кишки Портфолио учителя начальных классов Храбровой Ю.Н.
Портфолио учителя начальных классов Храбровой Ю.Н. Иврит. Фестиваль языков 2019
Иврит. Фестиваль языков 2019 Презентация доклада на РМО
Презентация доклада на РМО Образовательная программа детского объединения ателье Аленушка
Образовательная программа детского объединения ателье Аленушка Особливості декларування безпеки об’єктів підвищеної небезпеки
Особливості декларування безпеки об’єктів підвищеної небезпеки Противоэрозионная организация территории в границах КФХ Восток Белогорского района Амурской области
Противоэрозионная организация территории в границах КФХ Восток Белогорского района Амурской области Прокат спорт товаров
Прокат спорт товаров конспект внеклассного занятия Шоколад - есть или не есть! (согласно требованиям ФГОС ОО)
конспект внеклассного занятия Шоколад - есть или не есть! (согласно требованиям ФГОС ОО) Воспитательские позиции.
Воспитательские позиции. Модульное обучение на уроках биологии
Модульное обучение на уроках биологии Доклад Реализация личностно-ориентированного урока в 5-х классах
Доклад Реализация личностно-ориентированного урока в 5-х классах Производственный план
Производственный план Нравственно-патриотическое воспитание Диск
Нравственно-патриотическое воспитание Диск Порядок взаимодействия ЦПМПК г. Москвы с образовательными организациями
Порядок взаимодействия ЦПМПК г. Москвы с образовательными организациями Методическая разработка Учимся общаться, или общаемся играя
Методическая разработка Учимся общаться, или общаемся играя Буровые технологические жидкости. Основы физико-химии очистных агентов. (Лекция 2)
Буровые технологические жидкости. Основы физико-химии очистных агентов. (Лекция 2) Металлургия России
Металлургия России Загадки по лексической теме - Мебель
Загадки по лексической теме - Мебель презентация Здоровьесбережение в воспитательном процессе
презентация Здоровьесбережение в воспитательном процессе Теория черт личности. Рэймонд Бернард Кэттелл
Теория черт личности. Рэймонд Бернард Кэттелл Дары волхвов. По рассказу О. Генри
Дары волхвов. По рассказу О. Генри Религиозно-правовые школы в Исламе – мазхабы (ханафиты, ханбалиты, шафииты, маликиты; имамиты)
Религиозно-правовые школы в Исламе – мазхабы (ханафиты, ханбалиты, шафииты, маликиты; имамиты) Быстрее, выше, сильнее!
Быстрее, выше, сильнее! 70 лет Победы в ВОВ: Курская битва
70 лет Победы в ВОВ: Курская битва Гидравлический пресс
Гидравлический пресс