Решение систем конечных уравнений (СКУ) презентация

Если m>n, то система называется переопределённой.
Если m
При m=n, такая система называется нормальной системой уравнений.
СКУ можно разделить на два класса: линейные и нелинейные. СЛАУ содержат алгебраические функции с искомыми аргументами в первой степени во всех уравнениях системы.
Системы нелинейных уравнений делятся на алгебраические (содержат только алгебраические функции - многочлены n-ой степени с действительными коэффициентами) и трансцендентные (содержат тригонометрические, логарифмические и др.функции, не являющиеся многочленами).

Системы линейных алгебраических уравнений
Система уравнений называется совместной, если существует хотя бы одно решение этой системы, в противном случае она несовместна.
СЛАУ Au=f называется неоднородной, если найдётся хотя бы один свободный член fi ≠ 0, если все fi= 0, i=1,2,…n, то система называется однородной. Очевидно, что однородная система всегда совместна.
Тривиальное (нулевое) решение однородной СЛАУ Au=0 располагается в начале n-мерной системы координат:
u*=[0, 0,…,0]T
Если detA=0, то однородная СЛАУ имеет бесконечное множество решений.

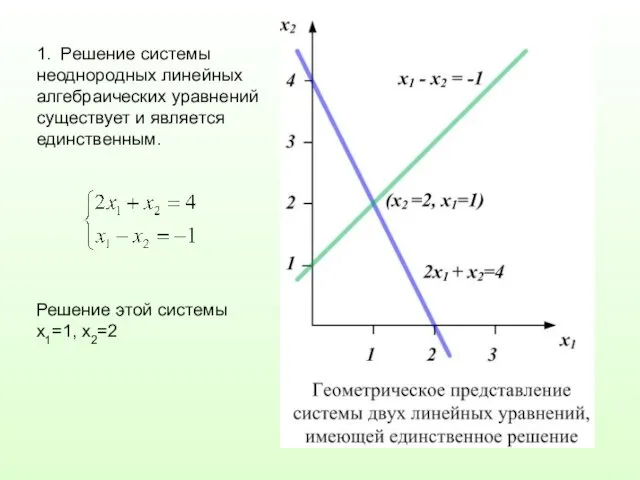
1. Решение системы неоднородных линейных алгебраических уравнений существует и является единственным.
Решение этой системы x1=1, x2=2

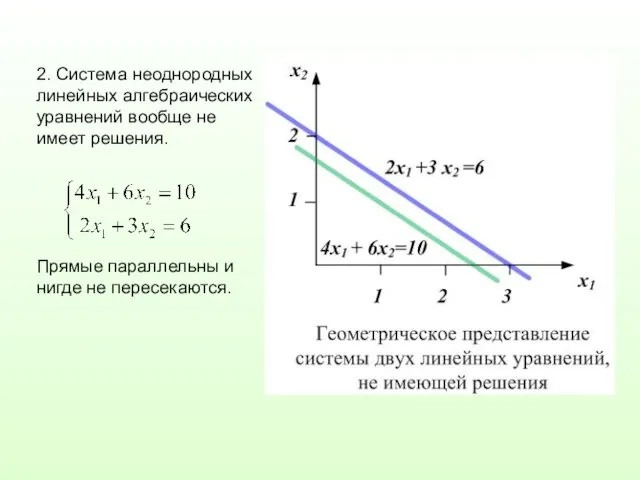
2. Cистема неоднородных линейных алгебраических уравнений вообще не имеет решения.
Прямые параллельны и нигде не пересекаются.

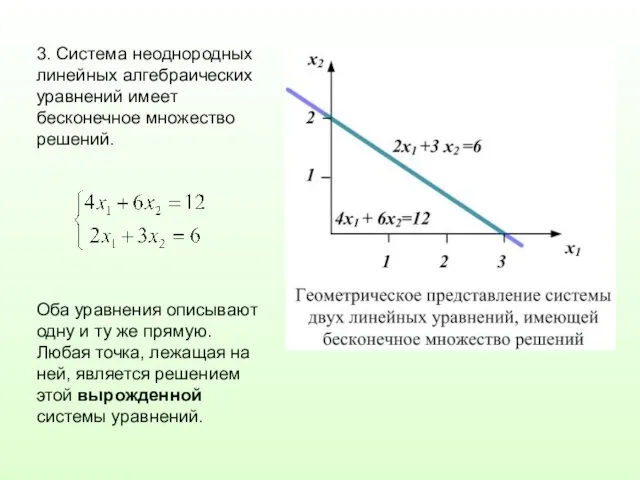
3. Система неоднородных линейных алгебраических уравнений имеет бесконечное множество решений.
Оба уравнения описывают одну и ту же прямую. Любая точка, лежащая на ней, является решением этой вырожденной системы уравнений.

Методы решения СЛАУ делятся на прямые
(в предположении отсутствия ошибок округления позволяют получить точные решения за конечное число арифметических действий) и итерационные или методы последовательных приближений (позволяют вычислить последовательность {uk} , сходящуюся к решению задачи при k→∞.
На практике ограничиваются конечным k в зависимости от требуемой точности. Однако неточность задания правых частей и элементов матрицы коэффициентов А может приводить к значительным погрешностям при вычислении решения СЛАУ.

Рассмотрим СЛАУ вида Au = f (2.1)
данным затратам машинного времени.

Если использовать наиболее оптимальный способ расчёта определителя, то для решения СЛАУ методом Крамера потребуется примерно арифметических операций.
Для сравнения матриц используются такие их характеристики, как определитель, ранг, матричные нормы.
Норма вектора и норма матрицы – это некоторые скалярные числовые характеристики, которые ставят в соответствие вектору и матрице.
Нормой вектора u = (u1, u2, …un)T (обозначают ║u║) в n-мерном вещественном пространстве векторов называют неотрицательное число, вычисляемое с помощью компонент вектора и обладающее следующими свойствами:
а) ║u║ ≥ 0 (║u║=0 тогда и только тогда, когда u – нулевой вектор);
б) ║α ∙ u║ = |α| ∙ ║u║ для любых чисел α (действительных или комплексных);
в) ║u+y║≤ ║u║ + ║y║.

Нормой матрицы Аn⋅n (обозначается ║А║) с вещественными элементами в пространстве матриц называют неотрицательное число, вычисляемое с помощью элементов матрицы и обладающее следующими свойствами:
а) ║А║ > 0 (║A║=0 тогда и только тогда, когда A – нулевая матрица);
б) ║α ∙ А║ = |α| ∙ ║А║ для любых чисел α (действительных или комплексных);
в) ║А+В║≤ ║А║ + ║В║;
г) ║А∙В║≤ ║А║ ∙ ║В║ для всех n x n матриц А и В рассматриваемого пространства.
Как видно из определения норм векторов и матриц (определения аналогичны, за исключением последнего свойства нормы матрицы), норма матрицы должна быть согласована с нормой векторов. Это согласование осуществляется следующей связью
║А∙u║≤ ║А║ ∙ ║u║

Согласованные с введёнными выше нормами векторов нормы матриц будут определяться следующим образом:
(2.3а)
(2.3б)
(2.3в)
и евклидова норма матрицы:
(2.3г)

Обусловленность СЛАУ
Число обусловленности матрицы

Пример. Вычислить число обусловленности для матрицы А.
Для этой матрицы detА = 10-4≠ 0 А-1= 104∙
║А║1 = 1,99; ║А-1║1 = 1,99∙104; μ(А) = 39601

Классический пример плохо обусловленной матрицы – матрица Гильберта: aij = 1/(i+ j – 1), i, j = 1,…,n.
Числа обусловленности для матриц Гильберта различных порядков
>>cond(hilb(n))

Прямы методы решения СЛАУ
Прямые методы дают решение за конечное число шагов. Они просты и универсальны. Их обычно используют для матриц порядка n< 104.
Трудность численного решения СЛАУ определяется видом матрицы А. Большое значение имеют её размер, обусловленность, симметричность, заполненность, специфика расположения ненулевых коэффициентов и др.
Легко получается решение системы с диагональной матрицей А: система распадается на n линейных уравнений, каждое из которых содержит лишь одну неизвестную величину.

Для диагональной системы очевидны явные формулы:

Метод исключения Гаусса

Если в методе Гаусса элемент на главной диагонали мал, то коэффициенты становятся большими числами, и при пересчёте элементов матрицы может быть значительная потеря точности на ошибках округления при вычитании больших чисел. Чтобы этого не происходило , перед исключением u1 среди элементов 1- ого столбца находится главный или максимальный элемент.
Этот метод называется методом Гаусса с выбором главного или ведущего элемента. Из-за накапливания погрешностей в процессе округления метод Гаусса без выбора главных элементов используется обычно для решения сравнительно небольших (n≤100) систем уравнений с плотно заполненной матрицей коэффициентов и не близким к нулю определителем. Если матрица А сильно разрежена, а её определитель при этом не близок к нулю, то метод Гаусса пригоден для решения больших систем уравнений.

При решении многих прикладных задач возникают разреженные матрицы, т.е матрицы, в которых много нулевых элементов. К ним относятся и трёхдиагональные матрицы. Метод прогонки разработан для решения систем уравнений с трёхдиагональной матрицей.
Для хранения квадратной матрицы А размерности nxn требуется n2 ячеек памяти и порядка n3 арифметических операций при работе с ней. Память, отводимая под хранение разреженной матрицы, пропорциональна количеству ненулевых элементов памяти. Оно вычисляется командой mnz(A). Количество арифметических операция также пропорционально mnz(A).

LU-разложение

Метод Холецкого (метод квадратного корня)
Пусть матрица А рассматриваемой линейной системы - симметричная, т.е. aij=aji, положительная матрица. Тогда она представима в виде A=LLT, где

Метод обратной матрицы
В матричном виде СЛАУ имеет вид Au=f .
Методом обратной матрицы решение системы может быть получено в результате умножения слева правой и левой частей этого уравнения на обратную матрицу от матрицы коэффициентов системы:
A-1Ax = A-1f
Учитывая, что A-1A = Е, получаем x = A-1f.
Этот метод удобно применять в тех случаях, когда несколько раз решается система уравнений с разными правыми частями. В этом случае достаточно один раз вычислить обратную матрицу A-1 и затем умножать её на различные векторы f.
Недостатком метода являются трудности вычисления обратной матрицы, особенно если она большой размерности или если её определитель близок к нулю.

Решение СЛАУ в MATLAB
В MATLAB имеется обширный арсенал методов решения СЛАУ. Для этого применяются следующие операторы:

prod(V) или prod(A,k) – вычисляет произведение элементов массива V или произведения столбцов или строк матрицы в зависимости от значения k;
>> V=[1,2,3];
>> prod (V) % произведение элементов вектора
>>A=[1 2;3 4]
>> prod(A) %произведения столбцов матрицы
>>prod(A,1) % произведения столбцов матрицы
>> prod(A,2) % произведения строк матрицы

sum(V) или sum(A,k) – вычисляет сумму элементов массива V или сумму столбцов или строк матрицы, в зависимости от значения k;
>>V=[-1 0 3 -2 1 -1 1]
>>sum(V) %сумма элементов вектора
>>C=[1 2 3;1 2 3]
>>sum(C,1) %сумма элементов матрицы по столбцам
>>sum(C,2) %сумма элементов матрицы по строкам

dot (v1,v2) – вычисляет скалярное произведение векторов v1 и v2, то же значение выдаст функция sum(v1.*v2);
>>v1=[1.2;0.3;-1.1]
>>v2=[-0.9;2.1;0.5]
>>dot (v1,v2) %скалярное произведение
>> sum(v1.*v2) %скалярное произведение
cross (v1,v2) – определяет векторное произведение векторов v1 и v2;
>>v1=[1.2;0.3;-1.1]
>>v2=[-0.9;2.1;0.5]
>>cross (v1,v2)

min(V) – находит минимальный элемент массива V, вызов в формате [k,n]=min(V) даёт возможность определить минимальный элемент k и его номер n в массиве;
max(V) - находит максимальный элемент массива V, вызов в формате [k,n]=max(V) определяет максимальный элемент k и его номер n в массиве;
>> V=[-1 0 3 -2 1 -1 1]
>> min(V)
>> max(V)
>> [k,n]=min(V)
>> [k,n]=max(V)
sort(V) – выполняет упорядочивание массива V
>> V=[-1 0 3 -2 1 -1 1]
>> sort(V) %сортировка по возрастанию
>> -sort(-V) % сортировка по убыванию.

det(M) – вычисляет определитель квадратной матрицы M;
rank(M) – определяет ранг матрицы M;
norm(M,p) – вычисляет различные виды норм матрицы М в зависимости от p (p=1, 2, inf, fro);
cond(M,p) – определяет число обусловленности матрицы M, основанное на норме p;
>> M=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]
>> norm(M) %норма матрицы М
>> cond(M) %число обусловленности матрицы М
>> norm(M,2) %вторая норма матрицы М, аналогично norm(M)
>> cond(M,2) %число обусловленности матрицы М для второй нормы, аналогично cond(M)

diag(V,n) или diag(V) – создаёт квадратную матрицу с элементами V на n-ой диагонали или элементами V на главной диагонали;
>> diag(V) %диагональная матрица, V на главной диагонали
>> diag(V,1) %диагональная матрица, V на первой диагонали
cat(n, A, B, …) – объединяет матрицы А и В и все входящие матрицы, аналогично [A,B].
inv(M) - вычисляет матрицу, обратную к М;
>> M=[2 1 -5 1;1 -3 0 -6;0 2 -1 2;1 4 -7 6]
>>P=inv(M)
>> M*P %проверка M*P=Е

linsolve(A,b) - pешение системы линейных уравнений A*x=b, вызов в формате linsolve(A,b,options) позволяет задать метод решения уравнения. Если задать функцию в виде [x,r]= linsolve(A,b), то она вернёт х – решение системы и r - ранг матрицы А;
В случае, когда для решения линейной системы используется знак \ , т.е. X=A\b , выбор метода остаётся за МАТL АВ.
>> A=[1 2 3;-2 -4 -6]; b=[5;6]
>>x= linsolve(A,b)
>>A*x %проверка – решение не верно
>> [x,r]= linsolve(A,b)
>> A=[2 -1 1;3 2 -5;1 3 -2]; b=[0;1;4]
>>x= linsolve(A,b); >>A*x % проверка – решение верно
>> [x,r]= linsolve(A,b)

rref(M) - осуществляет приведение матрицы М к треугольной форме, используя метод исключения Гаусса;
>>%Решение системы уравнений методом Гаусса
>> A=[2 -1 1;3 2 -5;1 3 -2]; b=[0;1;4]
>> C= rref([A b]) %приведение расширенной матрицы к треугольному виду
>>x=C(1:3,4:4) %выделение последнего столбца из матрицы – это решение системы уравнений
>> A*x %проверка

chol(M) - вычисляет разложение по Холецкому для положительно определённой симметрической матрицы М;
>> A=[10 1 1;2 10 1;2 2 10]
>>chol(A)
>> A = [1 2;1 1] %матрица не симметрическая
>>chol(A)
>> A = [3 1 -1 2;-5 1 3 -4;2 0 1 -1; 1 -5 3 -3] %матрица содержит отрицательные элементы
>>chol(A)

lu(M) – выполняет LU- разложение, возращает две матрицы: нижнюю треугольную L и верхнюю треугольную U;
qr(M) – выполняет QR – разложение, возвращает ортогональную матрицу Q и верхнюю треугольную R; Ортогональная матрица обладает свойством Q т = Q-1.
realmin и realmax – выводят соответственно минимально (после нуля) и максимально возможные числа.

% Решим систему, используя LU-разложение
[L1,U] = lu(A)
y = L1\b
x = U\y
[L2,U,P] = lu(A) % где Р - матрица перестановок
L2 = P*L1

Пример 3.

b1
b1

Задания.
Решить СЛАУ
Определить обусловленность матрицы коэффициентов.
2.
Проверить точность решения системы уравнений.

3. Решить СЛАУ
Проверить точность решения системы уравнений.

Приложение
Элементы матричной алгебры