Содержание
- 2. Построение сечений Построение сечений многогранников можно осуществлять на основании аксиом стереометрии и теорем о параллельности прямых
- 3. Построение сечений Построение на основании аксиом стереометрии и теорем о параллельности прямых и плоскостей -Задача №1
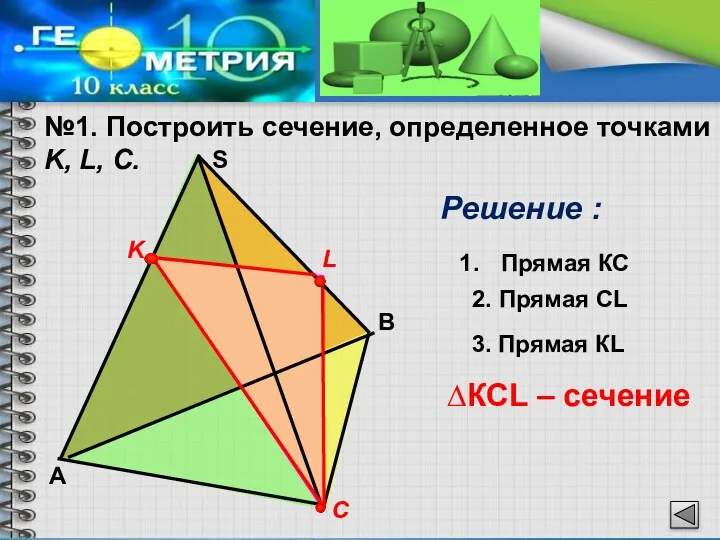
- 4. №1. Построить сечение, определенное точками K, L, С. Решение : K С L Прямая КС 2.
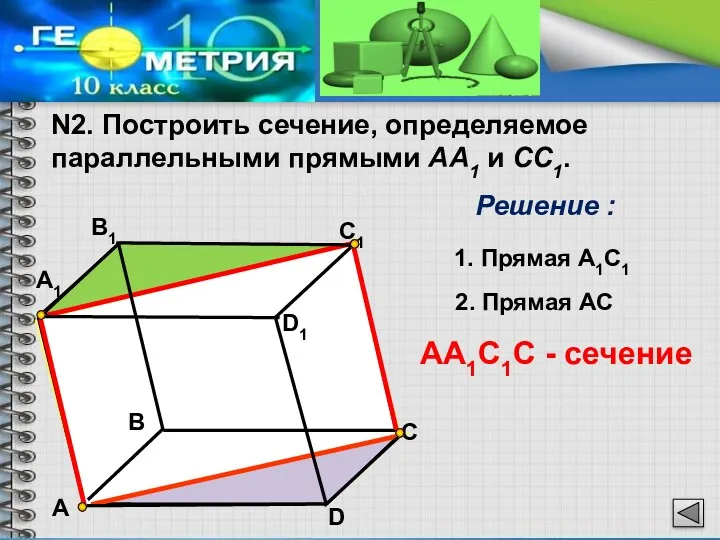
- 5. N2. Построить сечение, определяемое параллельными прямыми АА1 и CC1. А1 В1 С1 D1 С В D
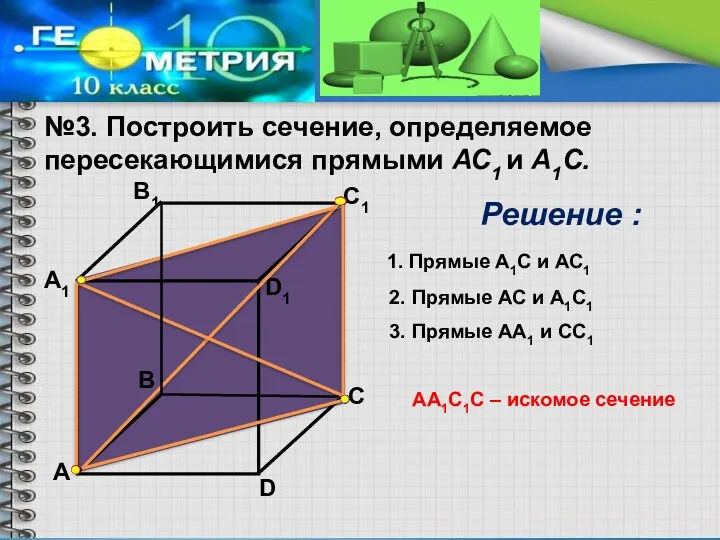
- 6. №3. Построить сечение, определяемое пересекающимися прямыми АС1 и А1С. А А1 В1 С1 D1 D В
- 7. Метод следов Прямая, по которой секущая плоскость α пересекает плоскость основания многогранника, называется следом плоскости α
- 8. Метод следов -Задача №4 -Задача №5 Построение сечений
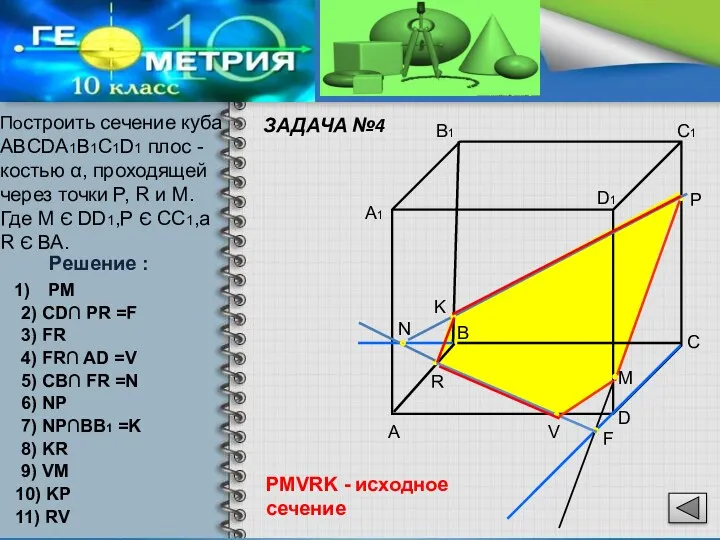
- 9. ЗАДАЧА №4 Построить сечение куба ABCDA1B1C1D1 плос -костью α, проходящей через точки P, R и M.
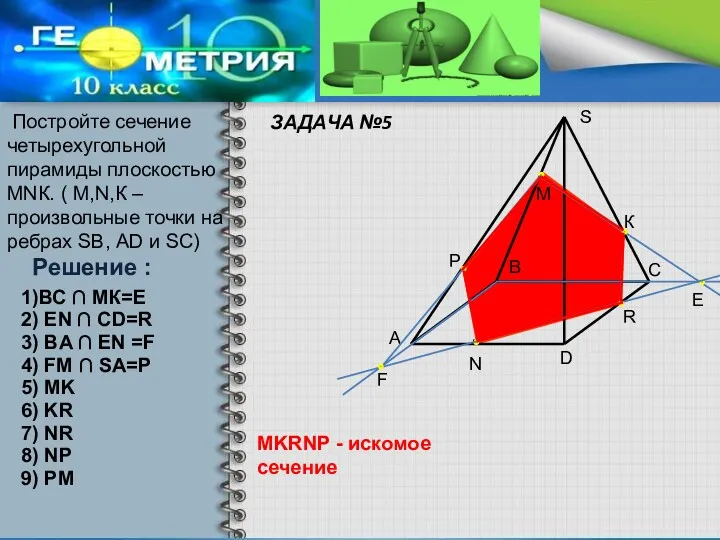
- 10. ЗАДАЧА №5 Постройте сечение четырехугольной пирамиды плоскостью МNК. ( М,N,К – произвольные точки на ребрах SВ,
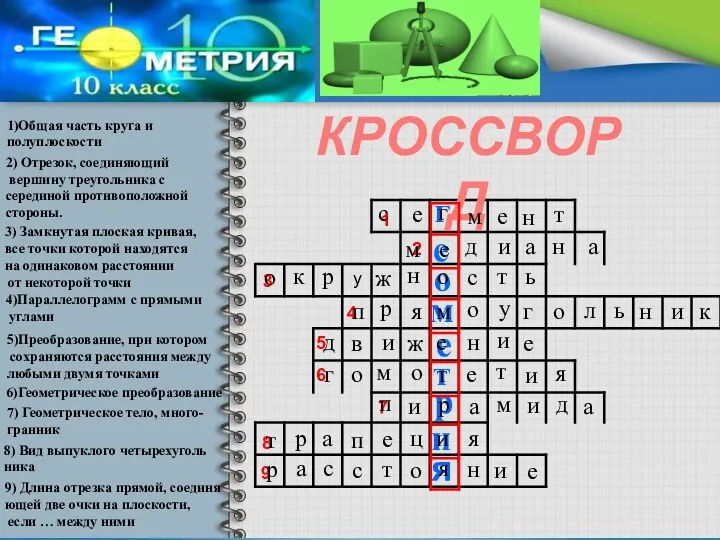
- 11. КРОССВОРД 1 2 3 4 5 6 7 8 9 1)Общая часть круга и полуплоскости 2)
- 12. Комбиниро-ванный метод Сущность этого метода состоит в том, что на некоторых этапах построения сечения применяется или
- 13. Метод внутреннего проектирования -Задача №6 -Задача №7 Комбинированный метод -Задача №8 Построение сечений
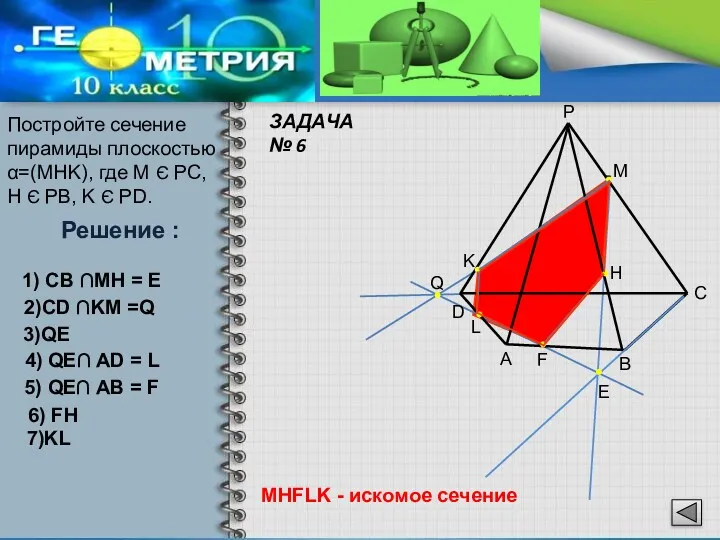
- 14. Постройте сечение пирамиды плоскостью α=(MHK), где M Є PC, H Є PB, K Є PD. D
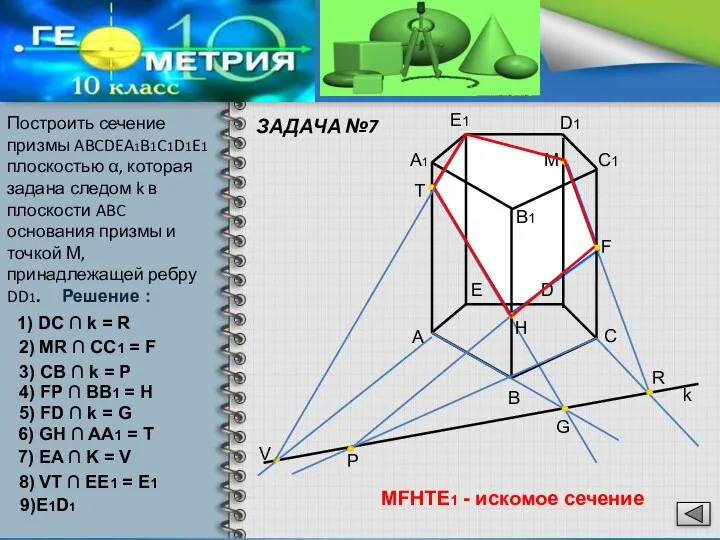
- 15. ЗАДАЧА №7 Решение : Построить сечение призмы ABCDEA1B1C1D1E1 плоскостью α, которая задана следом k в плоскости
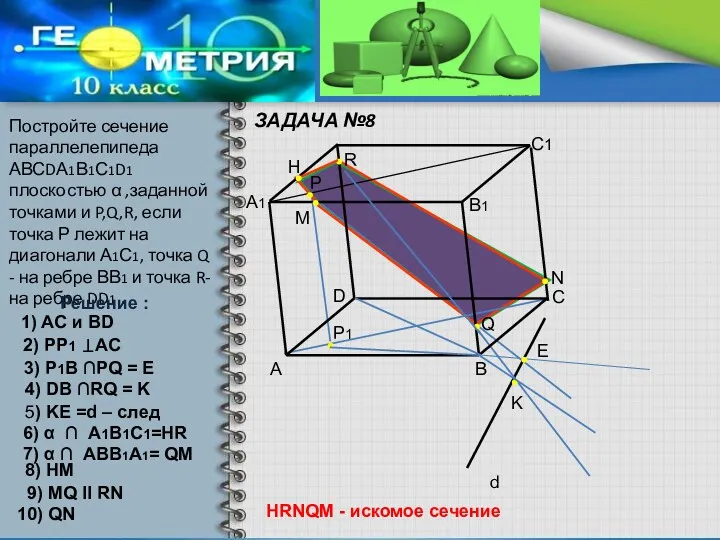
- 16. ЗАДАЧА №8 Постройте сечение параллелепипеда АВСDА1В1С1D1 плоскостью α ,заданной точками и P,Q,R, если точка Р лежит
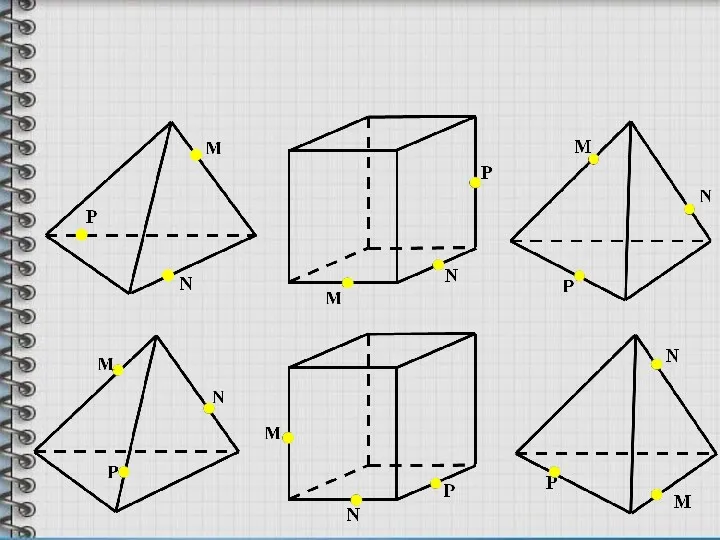
- 17. Самостоятельная работа. (с последующей проверкой)
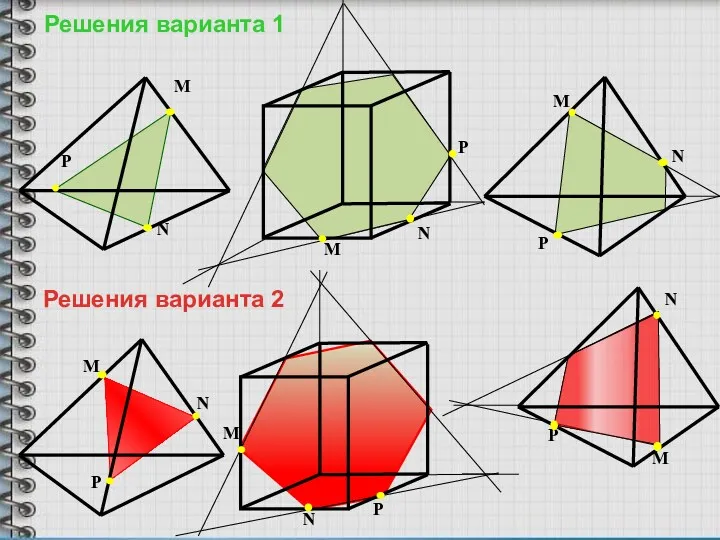
- 18. M N P M N P M N P Решения варианта 1 Решения варианта 2 M
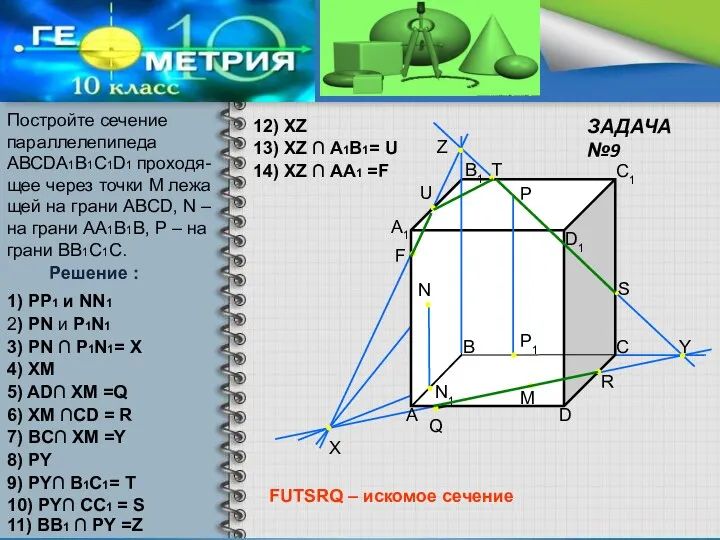
- 19. A A1 B B1 C C1 D D1 X N Y F U T Z M
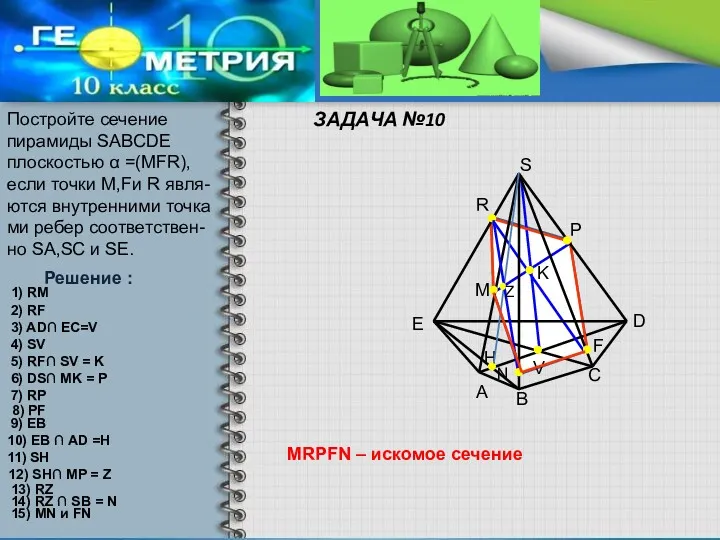
- 20. ЗАДАЧА №10 Постройте сечение пирамиды SАВСDЕ плоскостью α =(MFR), если точки M,Fи R явля- ются внутренними
- 23. Скачать презентацию







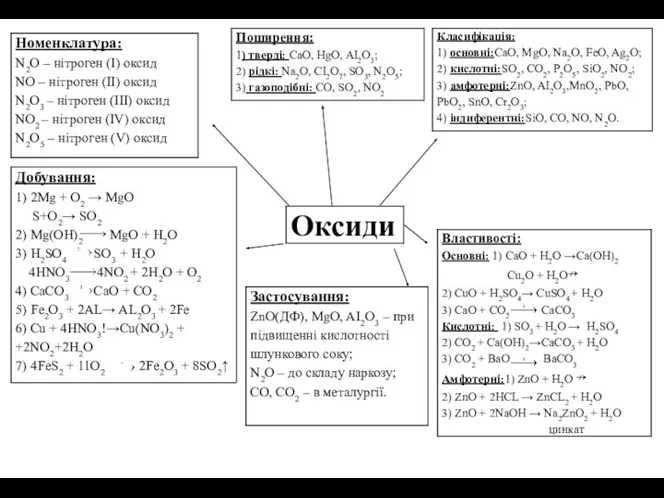 Нерганічна хімія
Нерганічна хімія Презентация к внеурочной деятельности Театр
Презентация к внеурочной деятельности Театр 中文课
中文课 Обмен энергии в организме человека
Обмен энергии в организме человека Великобритания: культура и искусство. Элективный курс. 9-й класс.
Великобритания: культура и искусство. Элективный курс. 9-й класс. Мы за здоровый образ жизни. Познавательный час
Мы за здоровый образ жизни. Познавательный час Особенности интеллектуальной сферы.Типы интеллекта
Особенности интеллектуальной сферы.Типы интеллекта МЭМС. Микроэлектромеханические системы
МЭМС. Микроэлектромеханические системы Организация онкологической помощи
Организация онкологической помощи Histoire de la littérature française
Histoire de la littérature française Системы сбора и подготовки нефти
Системы сбора и подготовки нефти Формирование количественных представлений, представлений о составе числа, числовой прямой у детей с речевыми нарушениями посредством использования дидактических игр в образовательной области Познание.
Формирование количественных представлений, представлений о составе числа, числовой прямой у детей с речевыми нарушениями посредством использования дидактических игр в образовательной области Познание. экологическая тропинка в детском саду
экологическая тропинка в детском саду Термическая обработка стали
Термическая обработка стали Історія засобів опрацювання інформаційних об’єктів
Історія засобів опрацювання інформаційних об’єктів Первый член Символа веры. Вера
Первый член Символа веры. Вера Методики обследования памяти в дошкольный, школьный возраст, у взрослых людей
Методики обследования памяти в дошкольный, школьный возраст, у взрослых людей Масленица
Масленица Лекція 3. Лінійні кола. Елементи схем. Еквівалентні перетворення для лінійних кіл
Лекція 3. Лінійні кола. Елементи схем. Еквівалентні перетворення для лінійних кіл Эксплуатация различных видов серверного программного обеспечения АИС и ее особенности
Эксплуатация различных видов серверного программного обеспечения АИС и ее особенности Методическое пособие Технология изготовления мозаичного панно из фетровой крошки
Методическое пособие Технология изготовления мозаичного панно из фетровой крошки Філософія як специфічний тип знання
Філософія як специфічний тип знання У меня растут года, будет и семнадцать. Где работать мне тогда, чем заниматься?. Выбор профессии
У меня растут года, будет и семнадцать. Где работать мне тогда, чем заниматься?. Выбор профессии 20181205_obrazy_skorbi_i_pechali
20181205_obrazy_skorbi_i_pechali Право_угл_Социальное государство_ понятие_ признаки_ функции_ модели
Право_угл_Социальное государство_ понятие_ признаки_ функции_ модели Загрузка изображений
Загрузка изображений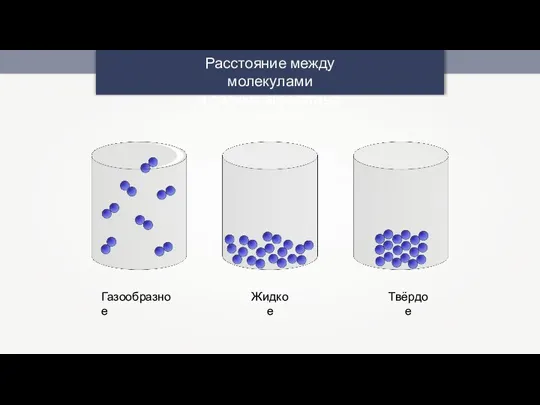 Жидкие вещества
Жидкие вещества Маркетинговый аудит
Маркетинговый аудит