Содержание
- 2. Свойства параллельных плоскостей
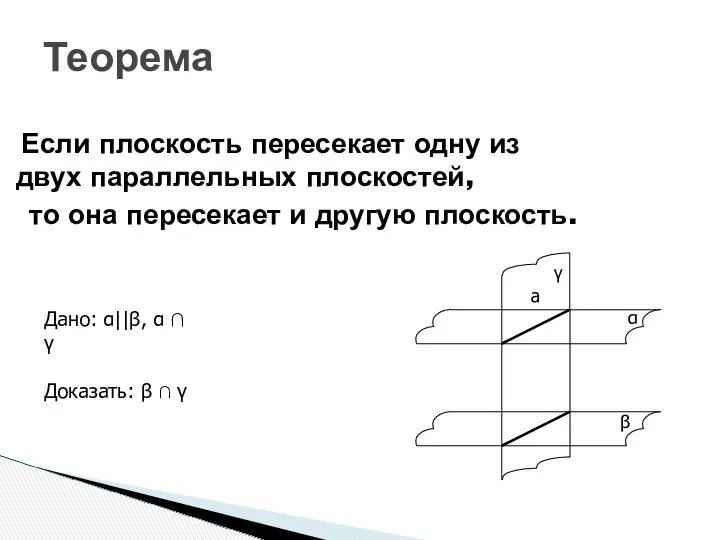
- 3. Теорема Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость. α
- 4. Доказательство Проведём в плоскости γ прямую а, пересекающую плоскость α в некоторой точке В. Тогда по
- 5. Теорема: Две плоскости, параллельные третьей, параллельны. Дано :α║β, γ║β. Доказать :α║γ. β γ α
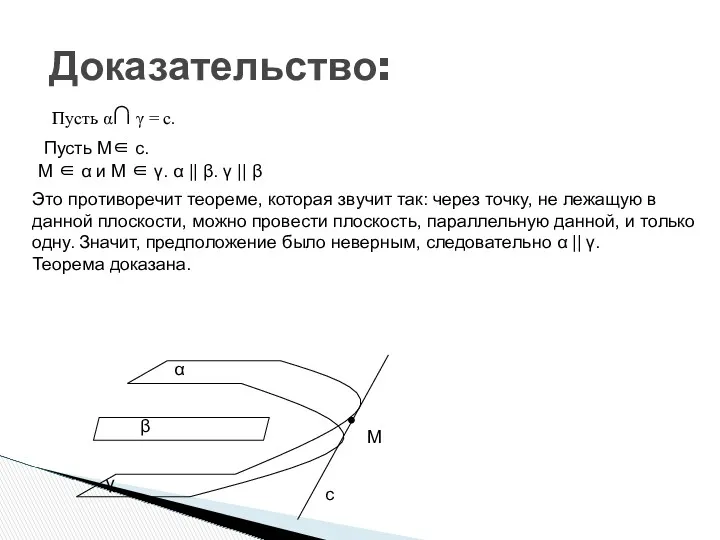
- 6. Доказательство: Пусть α∩ γ = с. с α β γ Пусть М∈ с. М ∈ α
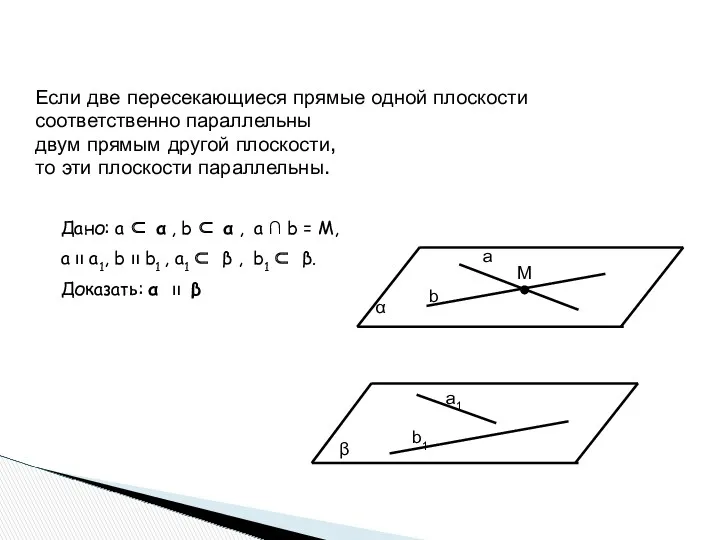
- 7. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
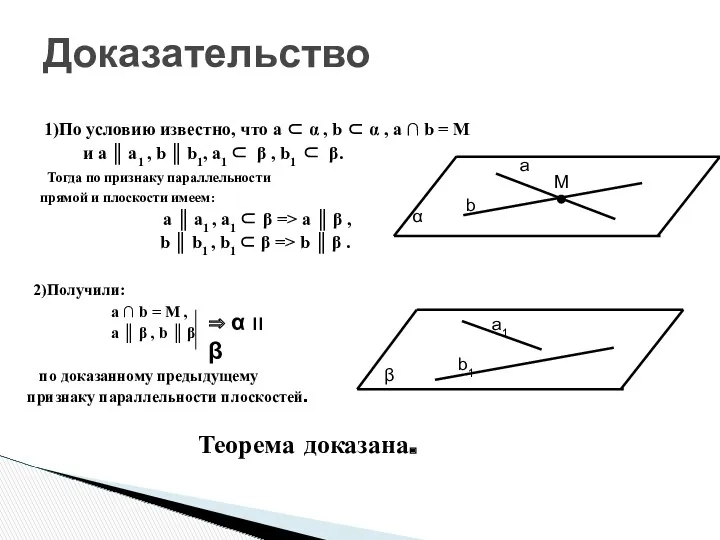
- 8. Доказательство 1)По условию известно, что a ⊂ α , b ⊂ α , a ∩ b
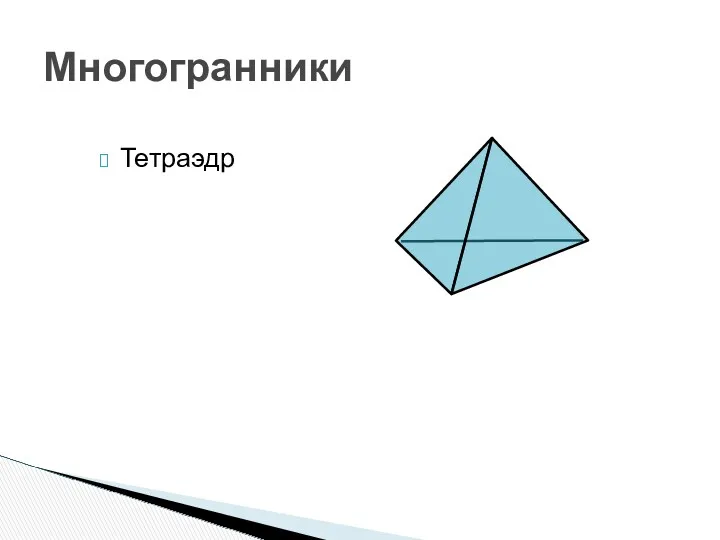
- 9. Многогранники Тетраэдр
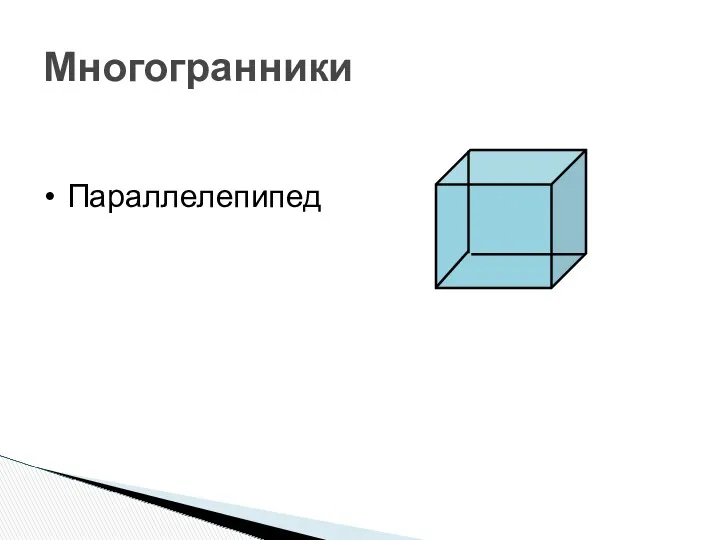
- 10. Многогранники Параллелепипед
- 11. Свойства тетраэдра Правильный Тетраэдр Тетра́эдр — многогранник с четырьмя треугольными гранями, в каждой из вершин которого
- 12. Параллелепипед Свойства Параллелепипед симметричен относительно середины его диагонали, соединяющей противоположные вершины. Диагонали параллелепипеда пересекаются в одной
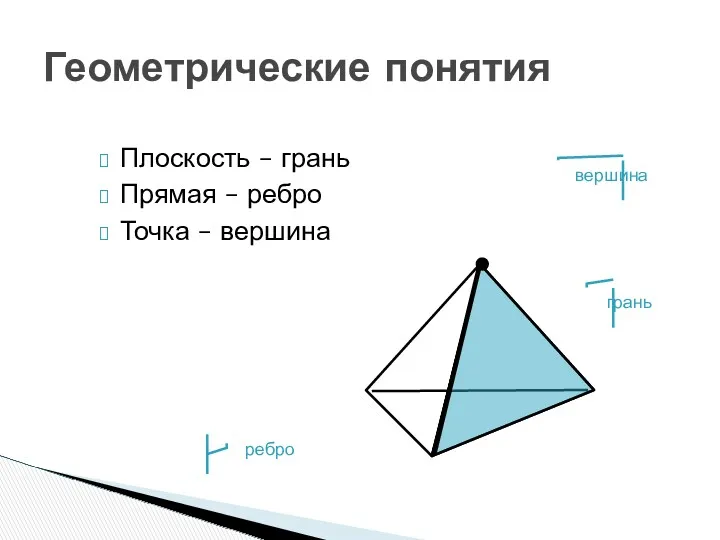
- 13. Геометрические понятия Плоскость – грань Прямая – ребро Точка – вершина грань ребро вершина
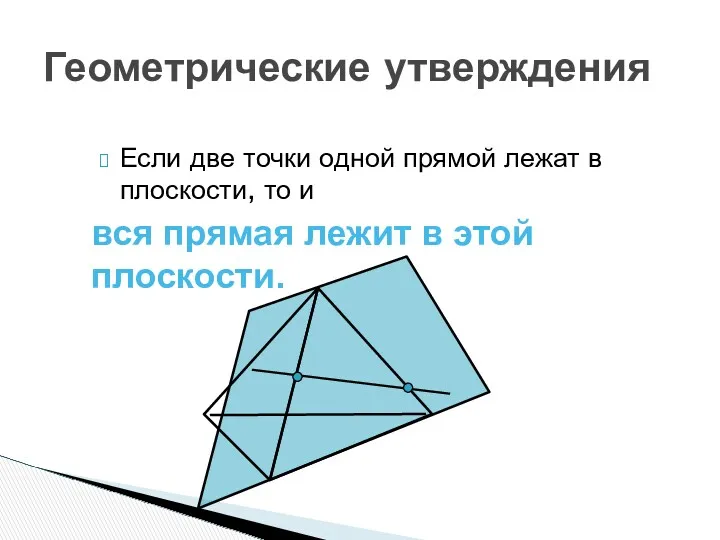
- 14. Геометрические утверждения Если две точки одной прямой лежат в плоскости, то и вся прямая лежит в
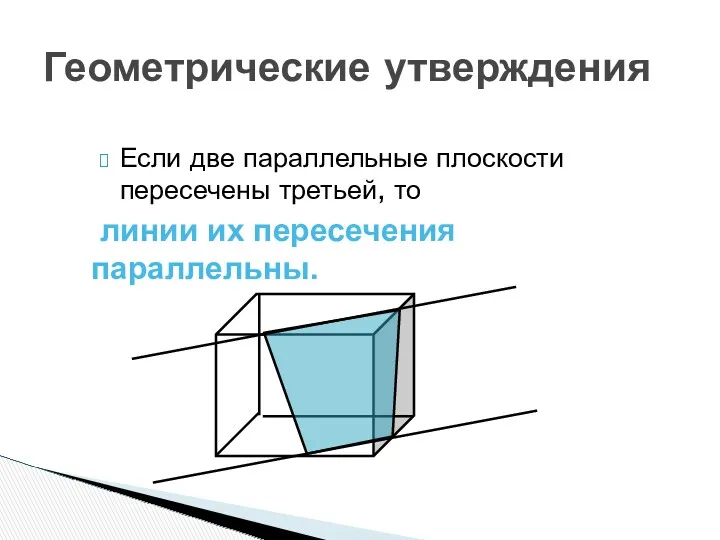
- 15. Геометрические утверждения Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
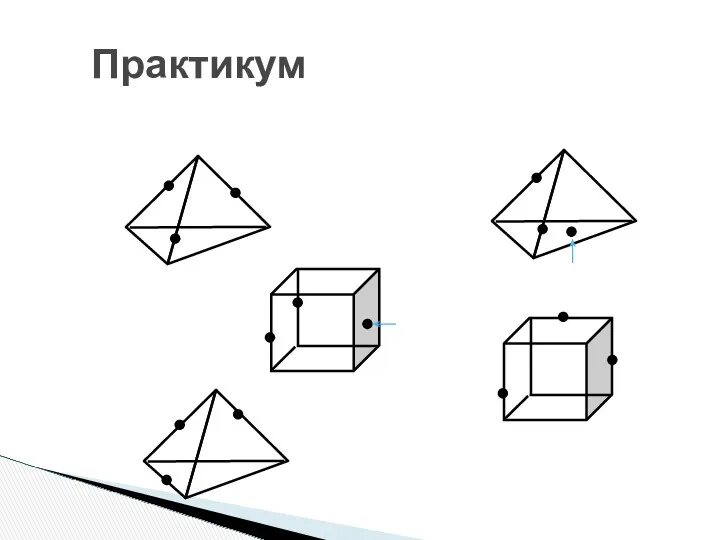
- 16. Практикум
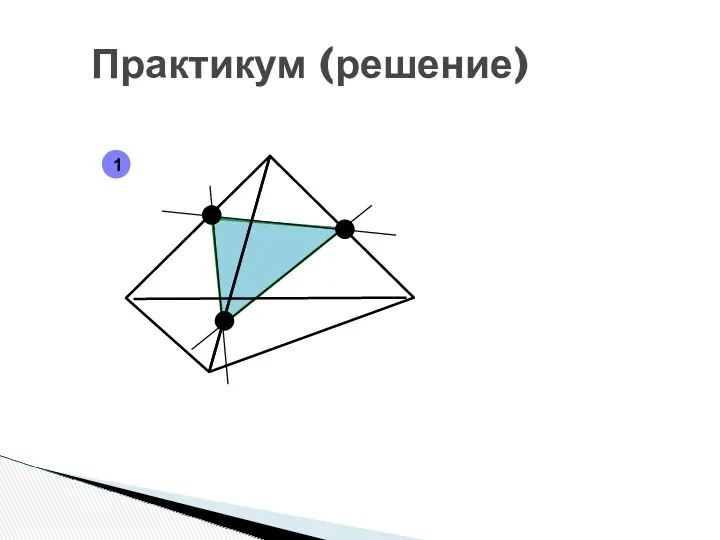
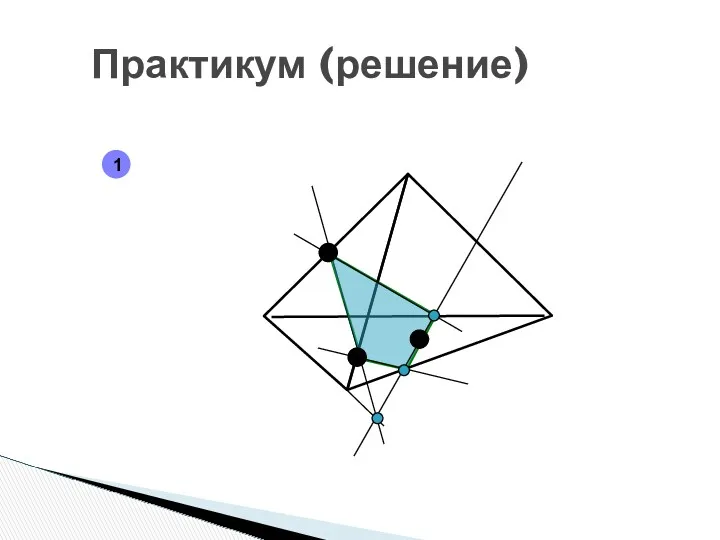
- 17. Практикум (решение) 1
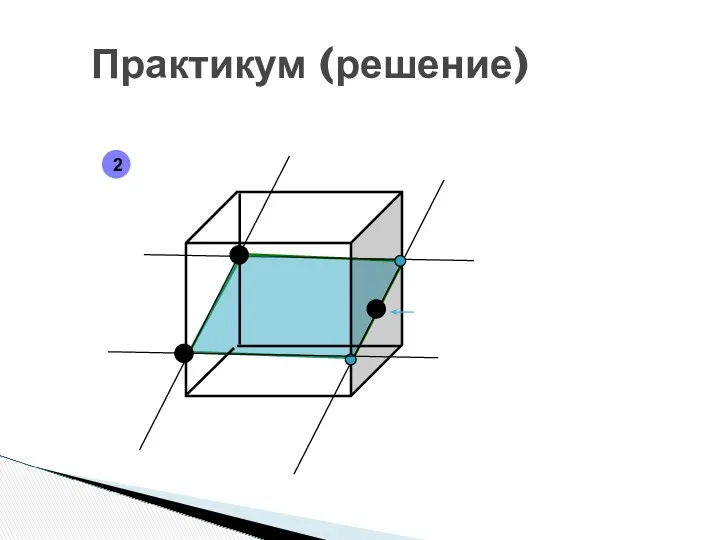
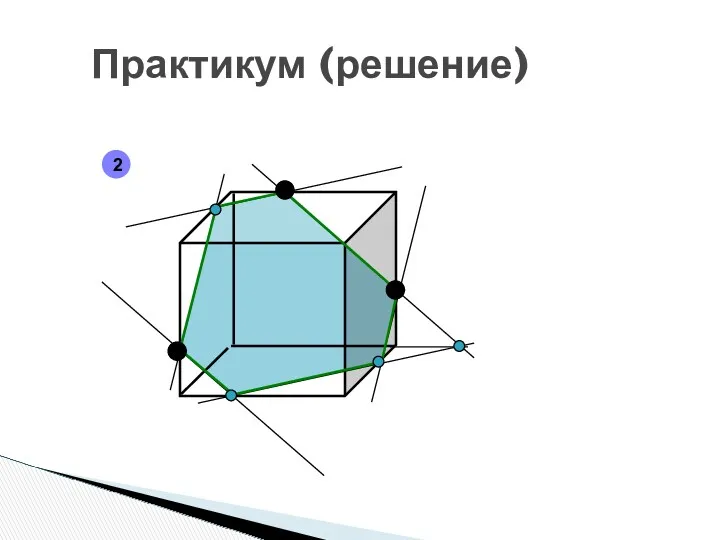
- 18. Практикум (решение) 2
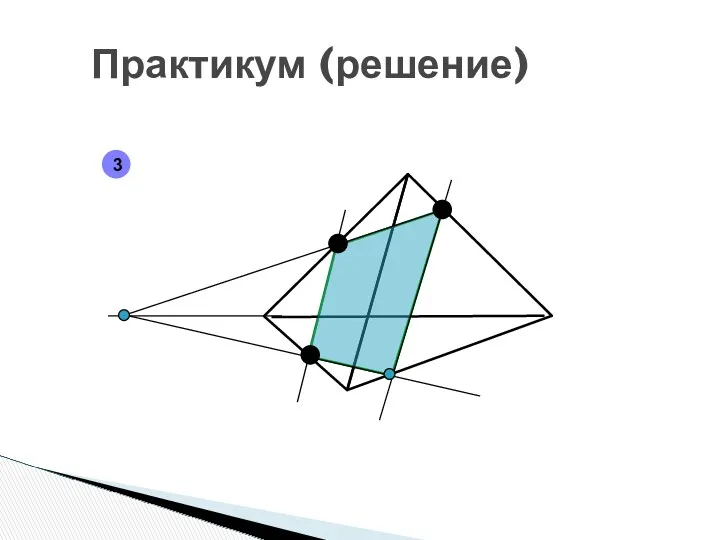
- 19. Практикум (решение) 3
- 20. Практикум (решение) 1
- 21. Практикум (решение) 2
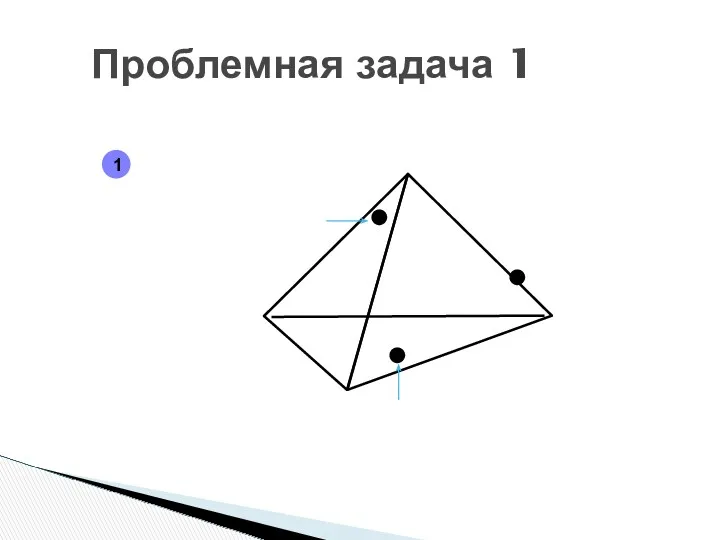
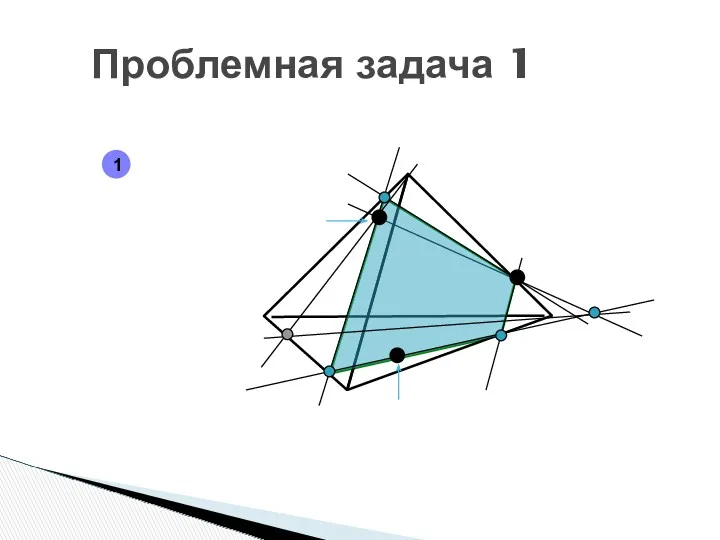
- 22. Проблемная задача 1 1
- 23. Проблемная задача 1 1
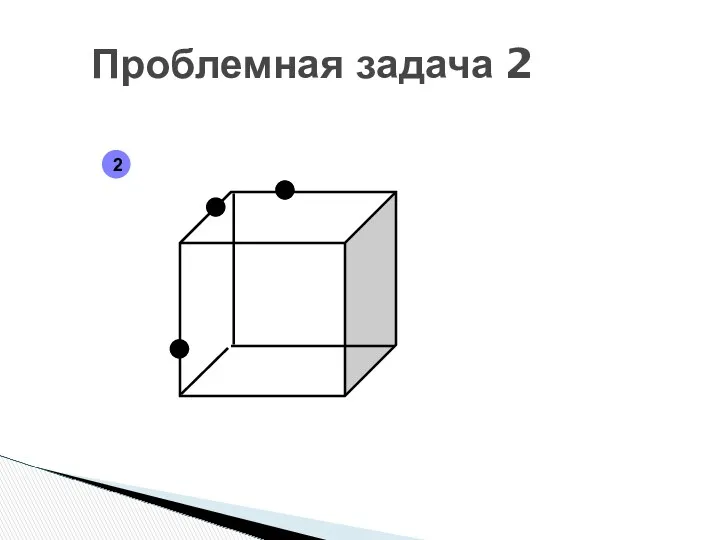
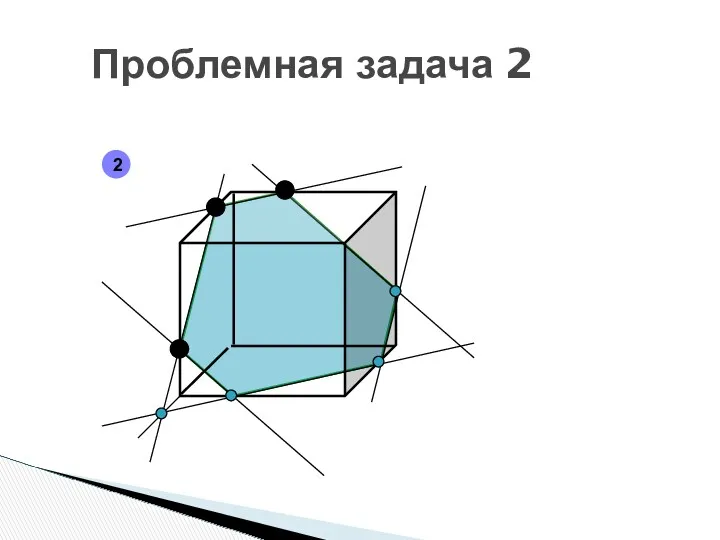
- 24. Проблемная задача 2 2
- 25. Проблемная задача 2 2
- 27. Скачать презентацию





 Лирика русского рока
Лирика русского рока Особенности перевода Complex Subject
Особенности перевода Complex Subject Совещание первосвященников об убиении Христа. Предательство Иуды
Совещание первосвященников об убиении Христа. Предательство Иуды Организация работы в специализированных (БИТ) и линейных бригадах скорой помощи
Организация работы в специализированных (БИТ) и линейных бригадах скорой помощи Презентация Белгородчина спортивная
Презентация Белгородчина спортивная ЧС гидрологического происхождения. Контрольное тестирование
ЧС гидрологического происхождения. Контрольное тестирование История почтовой открытки
История почтовой открытки Участковые станции
Участковые станции Вчера, сегодня,завтра. Активизация в речи правильного употребления времен глаголов
Вчера, сегодня,завтра. Активизация в речи правильного употребления времен глаголов А. А. Блок Двенадцать
А. А. Блок Двенадцать Разговор с родителями Поощрение или наказание
Разговор с родителями Поощрение или наказание Умный дом
Умный дом Способы решения квадратных уравнений
Способы решения квадратных уравнений Нарушения проводимости блокады сердца
Нарушения проводимости блокады сердца Сюжетно-ролевая игра
Сюжетно-ролевая игра MS Excel: основы работы
MS Excel: основы работы Конструктивные особенности станков с ЧПУ
Конструктивные особенности станков с ЧПУ Клуб Двойная навигация. Контроль давления. УЗИ. Нейростимулция
Клуб Двойная навигация. Контроль давления. УЗИ. Нейростимулция Международный аэропорт Париж-Шарль де Голль
Международный аэропорт Париж-Шарль де Голль Перевёрнутый треугольник (женский тип фигуры)
Перевёрнутый треугольник (женский тип фигуры) Формула объема прямоугольного параллелепипеда Диск
Формула объема прямоугольного параллелепипеда Диск Ауыздың кілегей қабығының гиперкератотикалық өзгерістері бар науқастарға көмекті жоспарлау
Ауыздың кілегей қабығының гиперкератотикалық өзгерістері бар науқастарға көмекті жоспарлау Фильтр оценки состояния для непрерывных систем (наблюдатель вектора состояния)
Фильтр оценки состояния для непрерывных систем (наблюдатель вектора состояния) Световые явления в живой и неживой природе
Световые явления в живой и неживой природе Презентация Огород на подоконнике
Презентация Огород на подоконнике Лепим ягоды и фрукты
Лепим ягоды и фрукты Мешочек для подарков — копия
Мешочек для подарков — копия Использование энергии газового потока дла выработки электрической энергии
Использование энергии газового потока дла выработки электрической энергии