Содержание
- 2. Умения по КТ Определять значение функции по значению аргумента при различных способах задания функции; описывать по
- 3. Найдите производную:
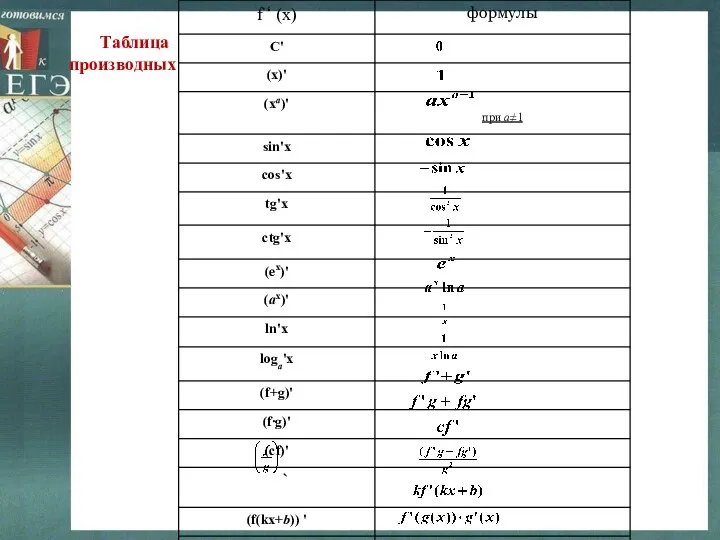
- 4. Таблица производных
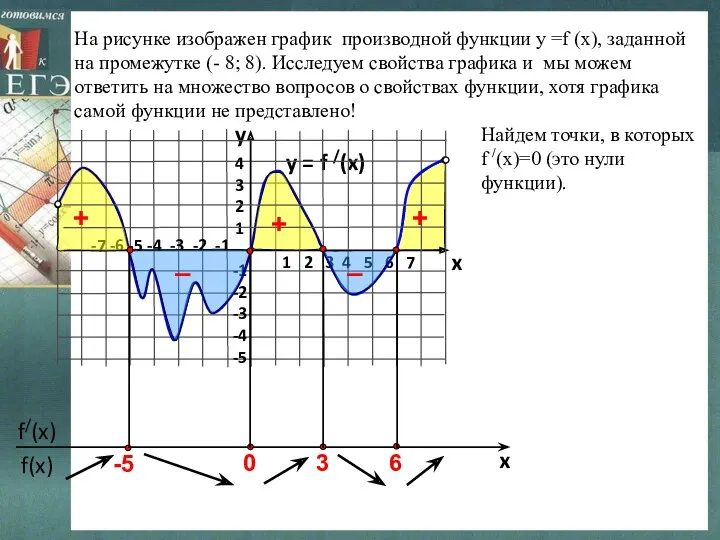
- 5. На рисунке изображен график производной функции у =f (x), заданной на промежутке (- 8; 8). Исследуем
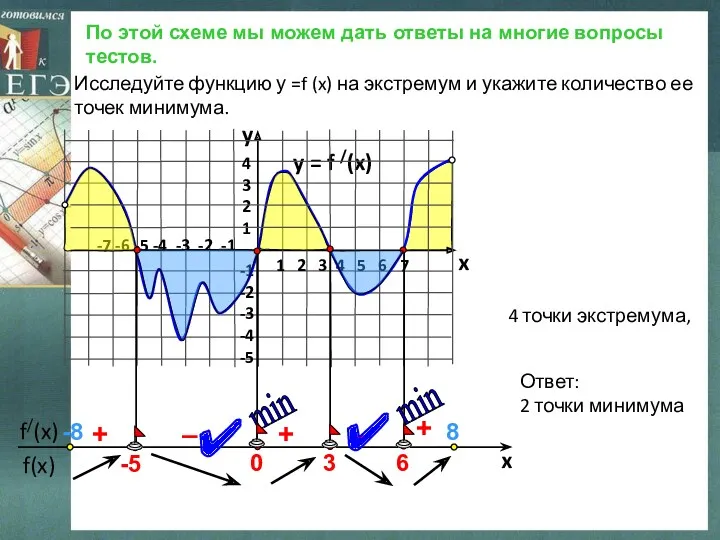
- 6. По этой схеме мы можем дать ответы на многие вопросы тестов. y = f /(x) 1
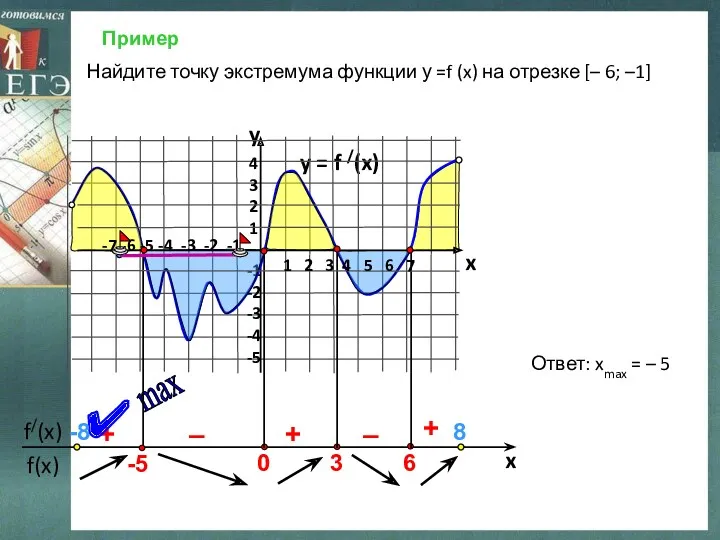
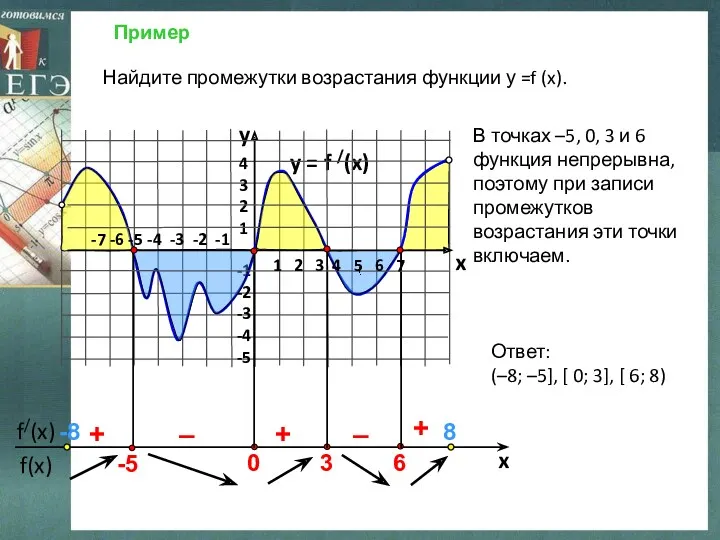
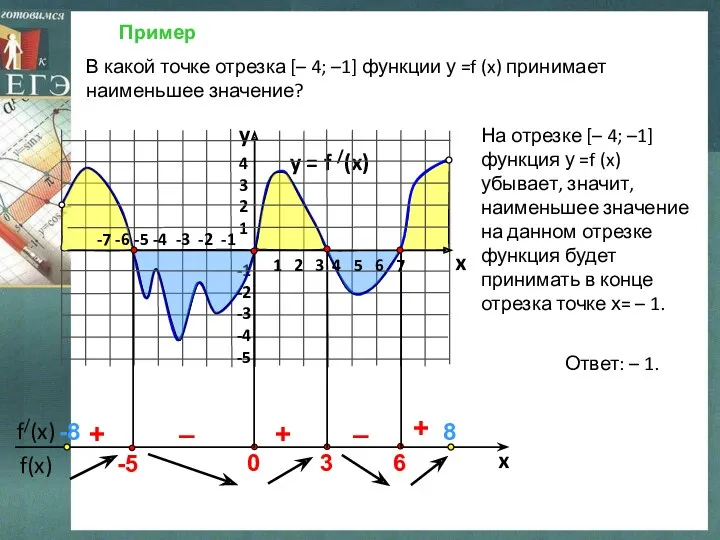
- 7. Пример y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x
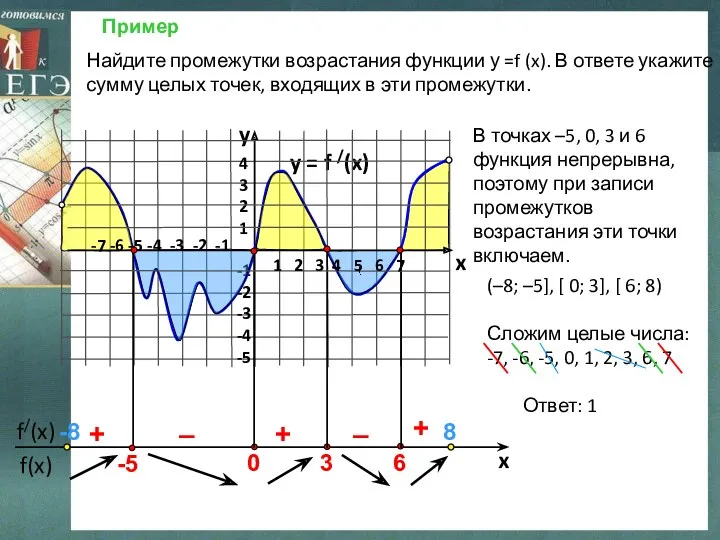
- 8. Пример y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x
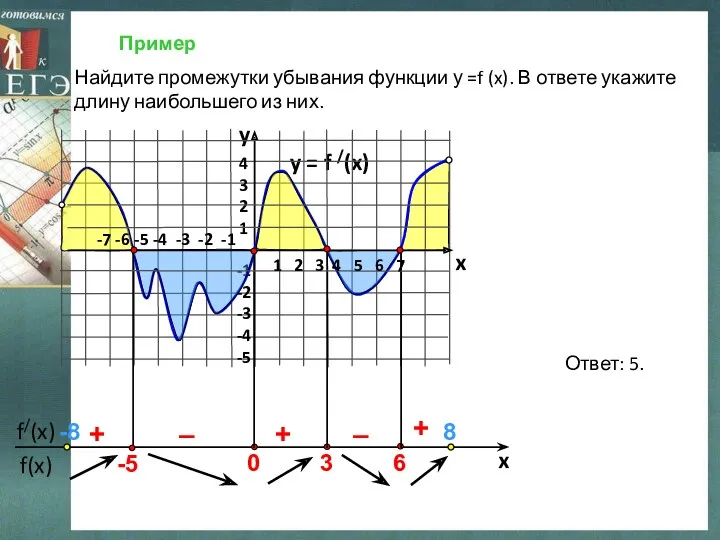
- 9. Пример y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x
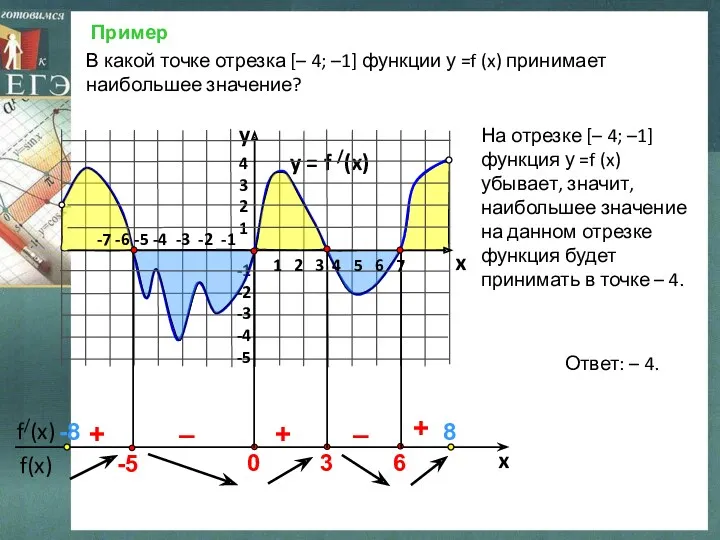
- 10. Пример y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x
- 11. Пример y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x
- 12. Пример y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x
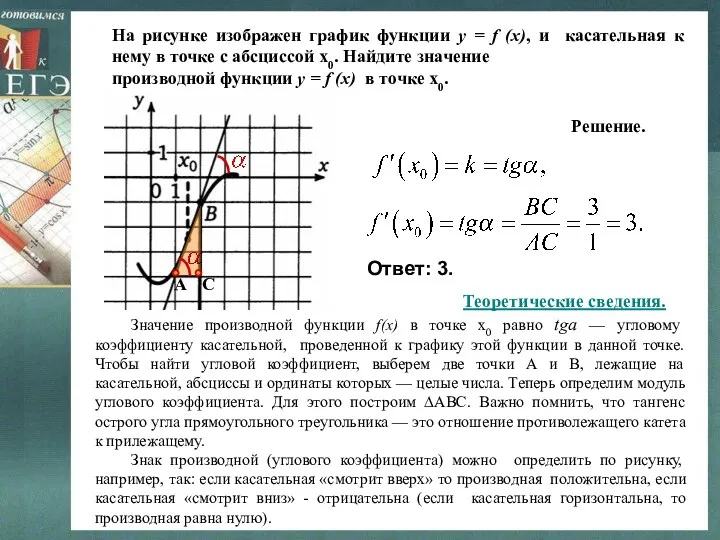
- 13. На рисунке изображен график функции y = f (x), и касательная к нему в точке с
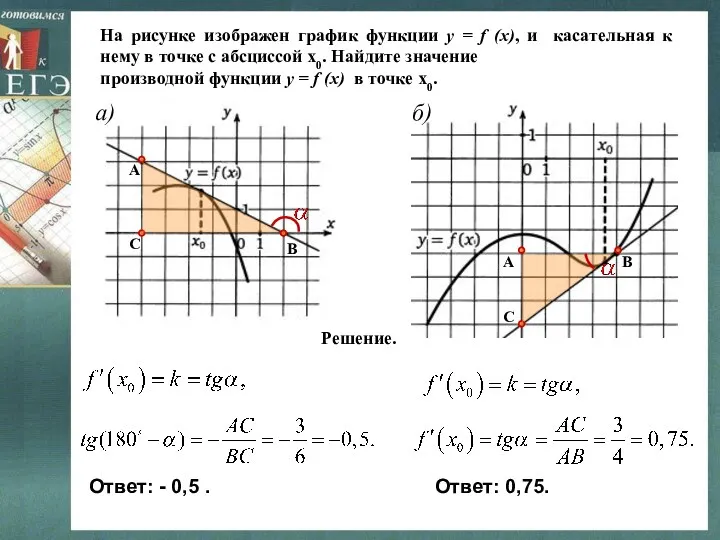
- 14. На рисунке изображен график функции y = f (x), и касательная к нему в точке с
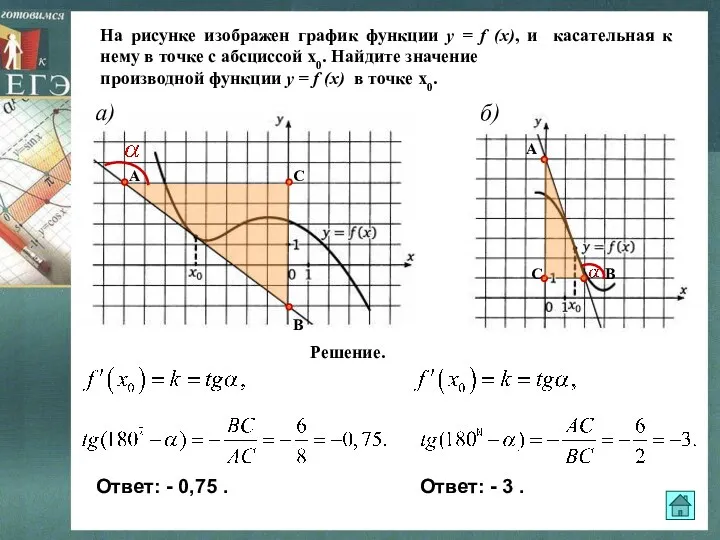
- 15. На рисунке изображен график функции y = f (x), и касательная к нему в точке с
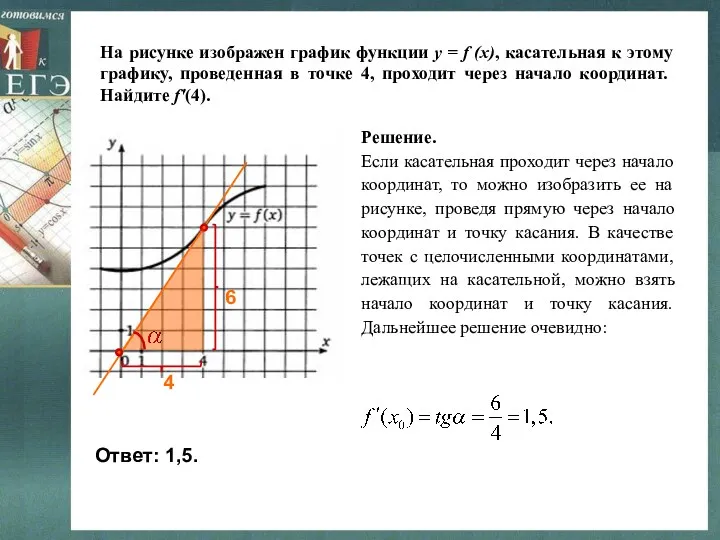
- 16. На рисунке изображен график функции y = f (x), касательная к этому графику, проведенная в точке
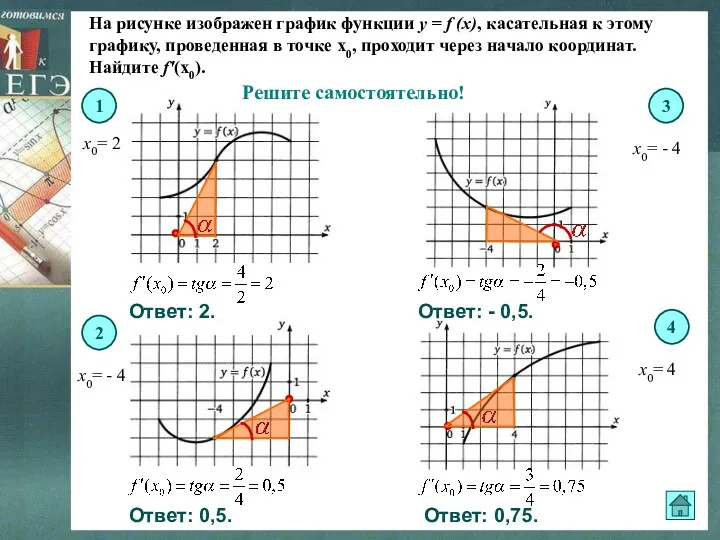
- 17. На рисунке изображен график функции y = f (x), касательная к этому графику, проведенная в точке
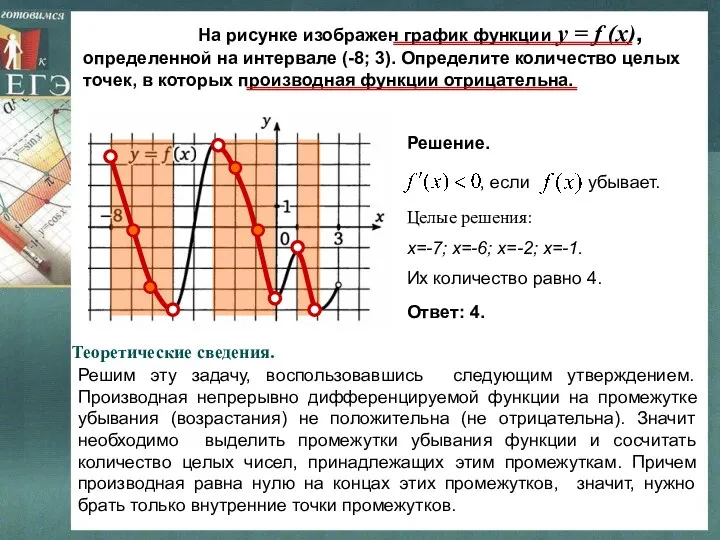
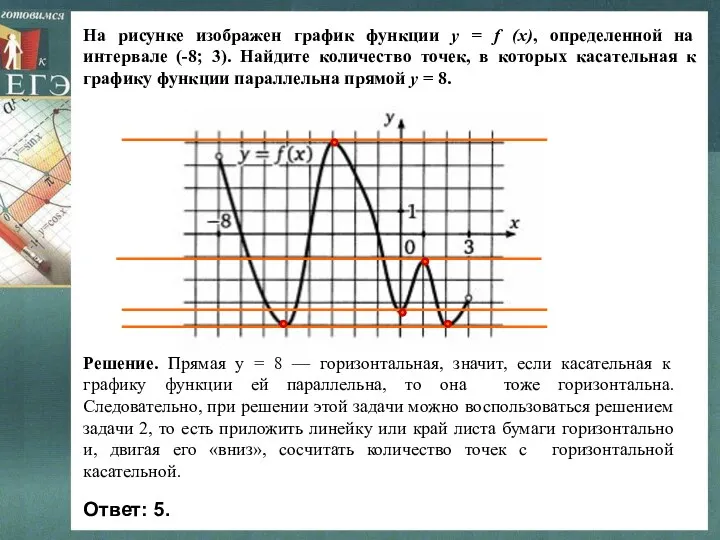
- 18. На рисунке изображен график функции y = f (x), определенной на интервале (-8; 3). Определите количество
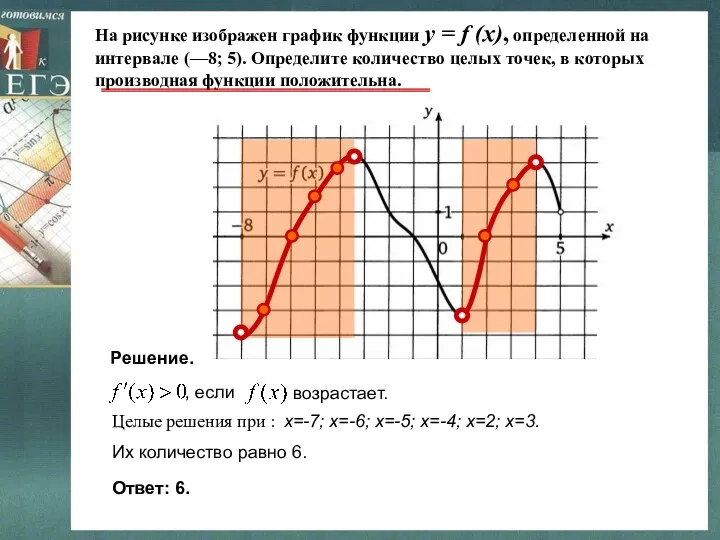
- 19. На рисунке изображен график функции y = f (x), определенной на интервале (—8; 5). Определите количество
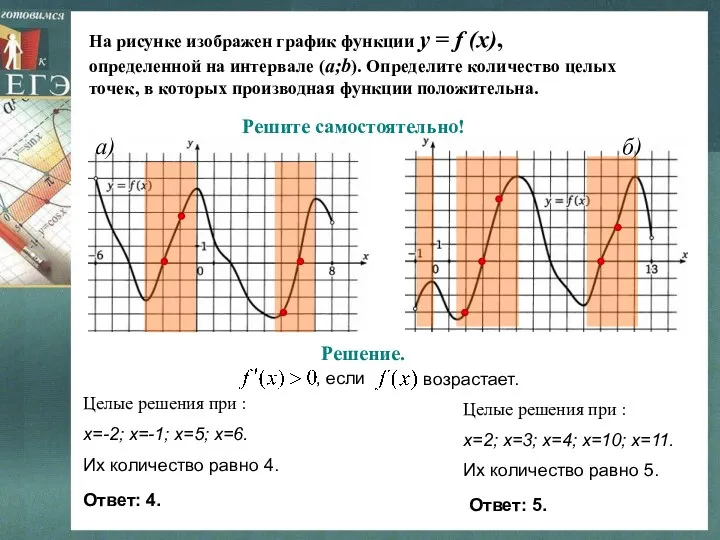
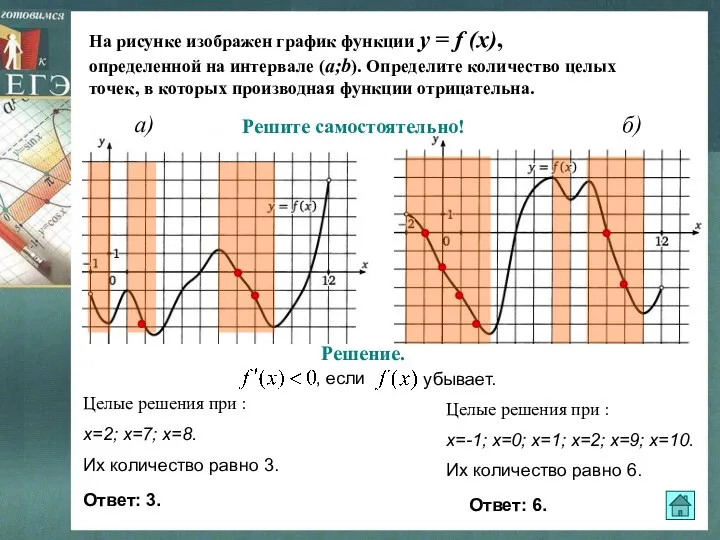
- 20. На рисунке изображен график функции y = f (x), определенной на интервале (a;b). Определите количество целых
- 21. На рисунке изображен график функции y = f (x), определенной на интервале (a;b). Определите количество целых
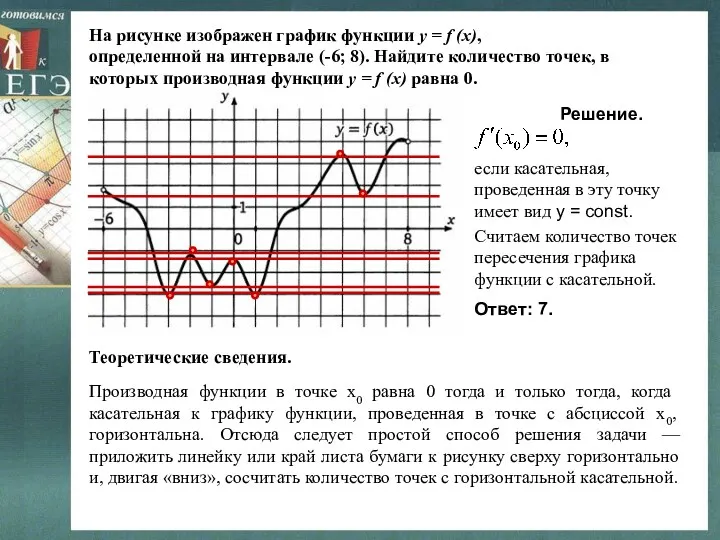
- 22. Производная функции в точке х0 равна 0 тогда и только тогда, когда касательная к графику функции,
- 23. На рисунке изображен график функции y = f (x), определенной на интервале (-8; 3). Найдите количество
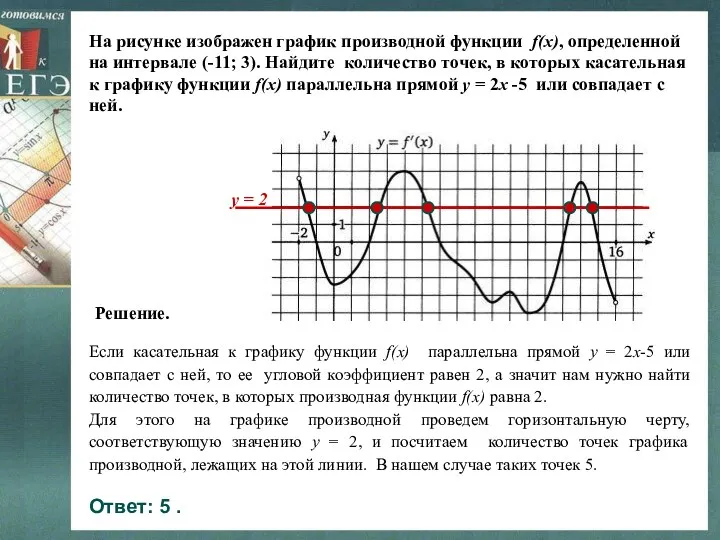
- 24. На рисунке изображен график производной функции f(x), определенной на интервале (-11; 3). Найдите количество точек, в
- 26. Скачать презентацию


 Презентация Сложение и вычитание десятичных дробей
Презентация Сложение и вычитание десятичных дробей Урок по теме: Длина окружности
Урок по теме: Длина окружности Презентация к уроку алгебры в 7 классе Решение систем способом подстановки.
Презентация к уроку алгебры в 7 классе Решение систем способом подстановки. Арифметическая и геометрическая прогрессии.
Арифметическая и геометрическая прогрессии. Сложение отрицательных чисел и чисел с разными знаками 6 класс
Сложение отрицательных чисел и чисел с разными знаками 6 класс Презентация: теорема Виета.
Презентация: теорема Виета. Физико-математический турнир для учащихся 8 классов
Физико-математический турнир для учащихся 8 классов 15 февраля в истории Кубани. Сложение и вычитание десятичных дробей.
15 февраля в истории Кубани. Сложение и вычитание десятичных дробей. Обобщающий урок по теме Проценты
Обобщающий урок по теме Проценты Презентация Раскрытие скобок
Презентация Раскрытие скобок Решение заданий С2 при подготовке к ЕГЭ
Решение заданий С2 при подготовке к ЕГЭ Презентация Золотое сечение.
Презентация Золотое сечение. математическая игра в 5 классе Своя игра
математическая игра в 5 классе Своя игра Внеклассное мероприятие по математике в 10 классе Своя игра
Внеклассное мероприятие по математике в 10 классе Своя игра Математический КВН 6 класс
Математический КВН 6 класс Математический конкурс - викторина.
Математический конкурс - викторина. План-конспект + презентация 6 класс Презентация
План-конспект + презентация 6 класс Презентация Разработка урока математики в 5 классе по теме Десятичная запись дробных чисел
Разработка урока математики в 5 классе по теме Десятичная запись дробных чисел призентация к уроку геометрии 10 кл ТТП
призентация к уроку геометрии 10 кл ТТП Презентация к уроку по теме Пропорции. 6 класс
Презентация к уроку по теме Пропорции. 6 класс Презентация по математике в 5 классе по теме Сложение и вычитание десятичных дробей
Презентация по математике в 5 классе по теме Сложение и вычитание десятичных дробей Это надо знать! (Алгебра)
Это надо знать! (Алгебра) Методическая разработка урока по математике в 6 классе по теме Масштаб
Методическая разработка урока по математике в 6 классе по теме Масштаб Презентация элективного курса по алгебре для 9 класса.
Презентация элективного курса по алгебре для 9 класса. Презентация Арктангенс числа а. Уравнение tgx=a
Презентация Арктангенс числа а. Уравнение tgx=a Общее понятие функции, способы её задания, свойства функции.
Общее понятие функции, способы её задания, свойства функции. урок алгебры в 9 классе по теме Последовательности
урок алгебры в 9 классе по теме Последовательности Презентация для урока по алгебре 7 класс
Презентация для урока по алгебре 7 класс