Начертательная геометрия. Условное обозначение и символы презентация

Условное обозначение и символы
⊂ - включение (содержит в себе)
∈ - принадлежность
⇒ - логическое следствие
∩ - пересечение
≡ - совпадение
⊥ - перпендикулярность
⏐⏐- параллельность
- скрещивание
( АВ ) – прямая, проходящая через точки А и B
[ АВ ] – отрезок прямой, ограниченный точками А и B
| АВ | – расстояние между точками А и B

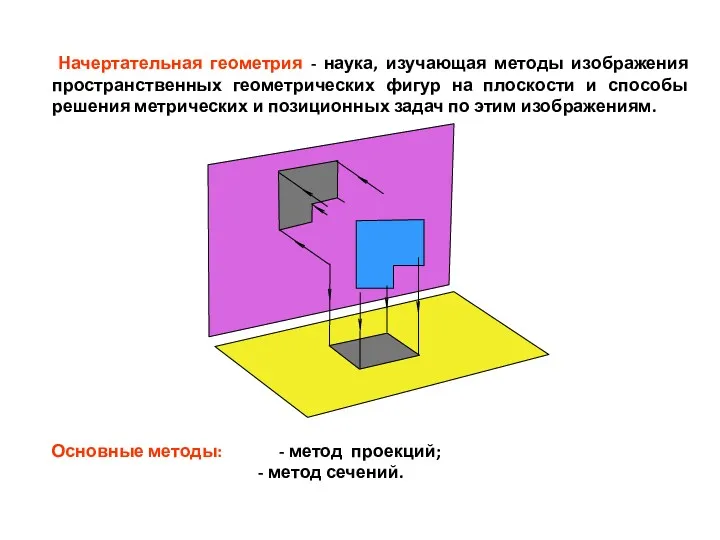
Начертательная геометрия - наука, изучающая методы изображения пространственных геометрических фигур на плоскости и способы решения метрических и позиционных задач по этим изображениям.
Основные методы: - метод проекций;
- метод сечений.

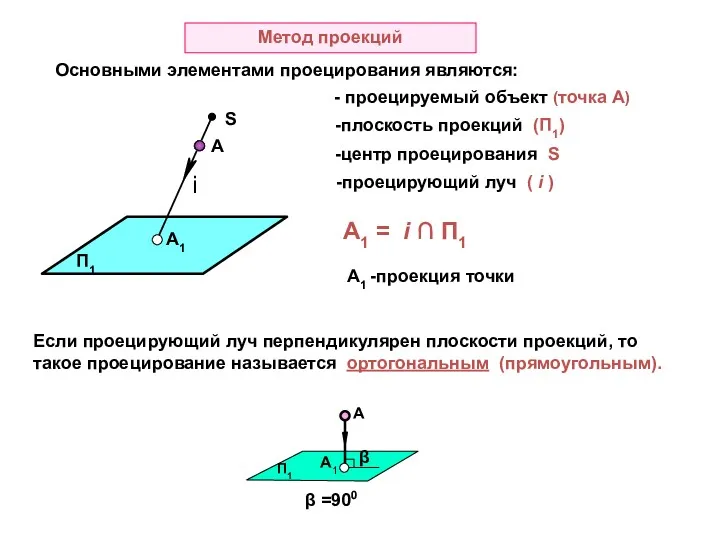
Метод проекций
Основными элементами проецирования являются:
А
А1
i
- проецируемый объект (точка А)
-плоскость проекций (П1)
-проецирующий луч ( i )
А1 -проекция точки
А1 = i ∩ П1
S
-центр проецирования S
Если проецирующий луч перпендикулярен плоскости проекций, то такое проецирование называется ортогональным (прямоугольным).
А
А1
П1
β =900
β

Обратимость чертежа
Требования к чертежу:
1.Точность
2. Наглядность
3. Обратимость
Обратимость чертежа обеспечивается проецированием на две (три) взаимно перпендикулярные плоскости проекций
восстановление оригинала по его проекционным изображениям (чертежу) – возможность определять форму, размеры объекта и его положение в пространстве.
a
b
c
a1 ≡ b1 ≡c1

П1
П2
П3
П1 – горизонтальная плоскость проекций
П3 – профильная плоскость проекций
Х
X - ось абсцисс
Z – ось аппликат
1 октант
2 октант
3 октант
4 октант
Z
Y – ось ординат
П2 – фронтальная плоскость проекций
У
Ортогональное проецирование
-У
-Z

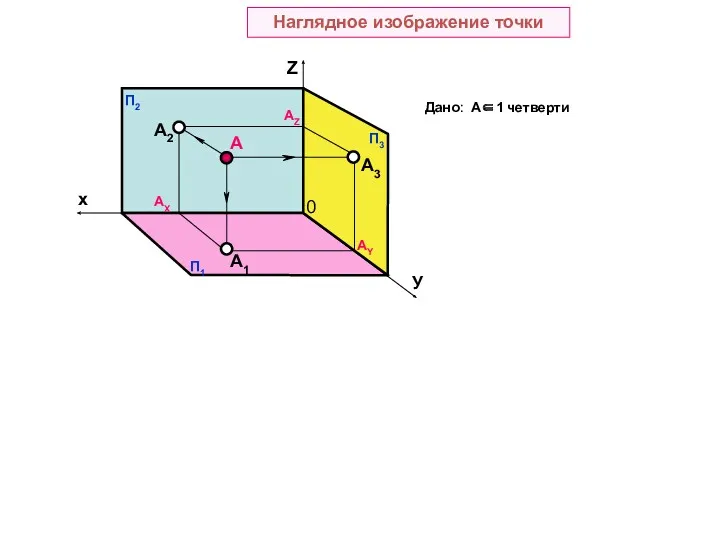
A
A1
A2
A3
АX
AY
AZ
Наглядное изображение точки
Дано: А∈1 четверти
0

A
A1
A2
A3
АX
AY
AZ
X
Y
Z
Наглядное изображение точки
Дано: А∈1 четверти
0
А1 (Х, )
А2 (Х, )
А3 (Y, Z)
Y
Z
Положение точки А в пространстве однозначно определяется координатами:
А ( X Y Z )

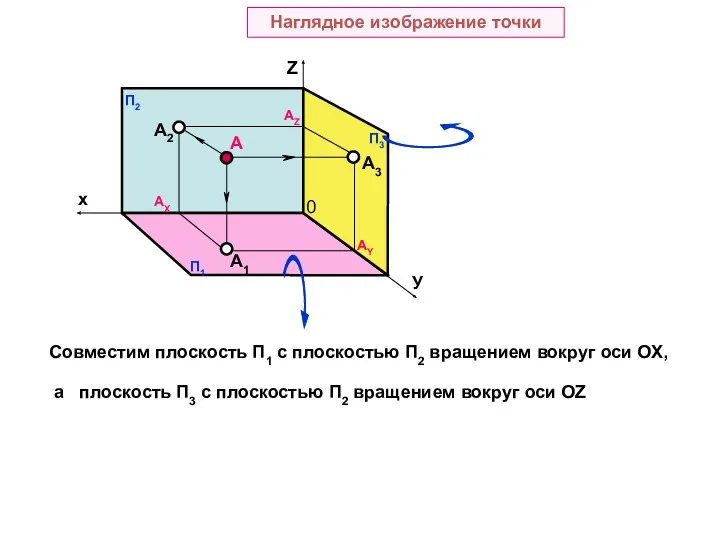
A
A1
A2
A3
АX
AY
AZ
Наглядное изображение точки
0
Совместим плоскость П1 с плоскостью П2 вращением вокруг оси ОХ,
а плоскость П3 с плоскостью П2 вращением вокруг оси ОZ

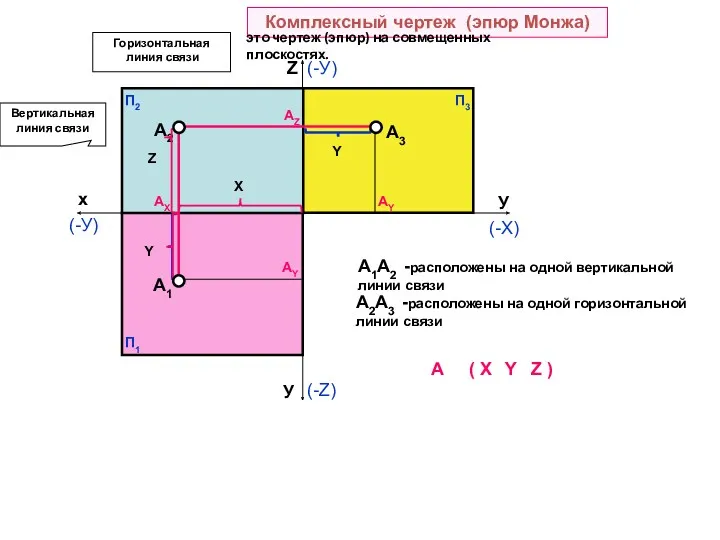
У
A1
A2
A3
AX
AY
AZ
П1
П2
П3
У
AY
0
Комплексный чертеж (эпюр Монжа)

У
A1
A2
A3
AX
AY
AZ
П1
П2
П3
А ( X
У
AY
Вертикальная линия связи
Горизонтальная
линия связи
Y
Z )
(-У)
(-Х)
(-Z)
(-У)
X
Y
Z
Комплексный чертеж (эпюр Монжа)
A1A2 -расположены на одной вертикальной линии связи
A2A3 -расположены на одной горизонтальной линии связи
это чертеж (эпюр) на совмещенных плоскостях.
Y

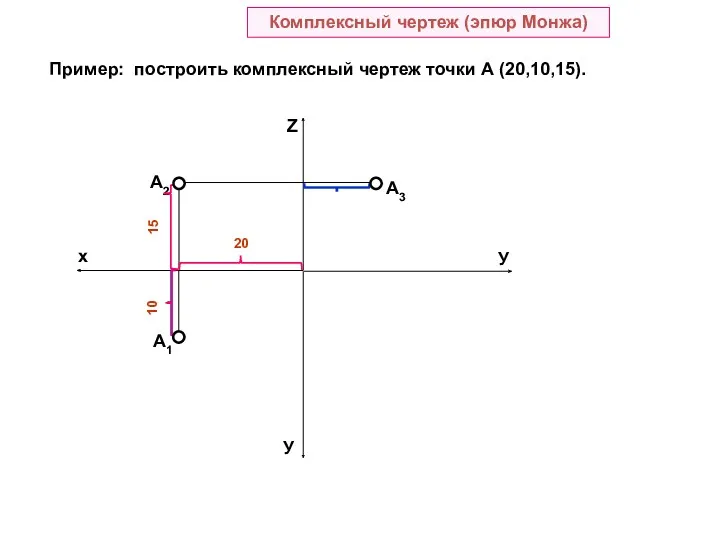
У
A1
A2
A3
У
20
10
15
Комплексный чертеж (эпюр Монжа)
Пример: построить комплексный чертеж точки А (20,10,15).

M1
N1 ≡B1
( )
П1
П2
A
M1
M
A1
M2 ≡A2
B
N
N1 ≡B1
N2
B2
A1
M2 ≡A2
B2
N2
( )
( )
( )
Конкурирующие точки
Конкурирующие точки - это точки, расположенные на одном проецирующем луче.
Фронтально- конкурирующие точки
Горизонтально- конкурирующие точки
Из двух фронтально-конкурирующих точек видна та точка, которая наиболее удалена от фронтальной плоскости проекций
Из двух горизонтально- конкурирующих точек видна та точка, которая расположена выше относительно горизонтальной плоскости проекций

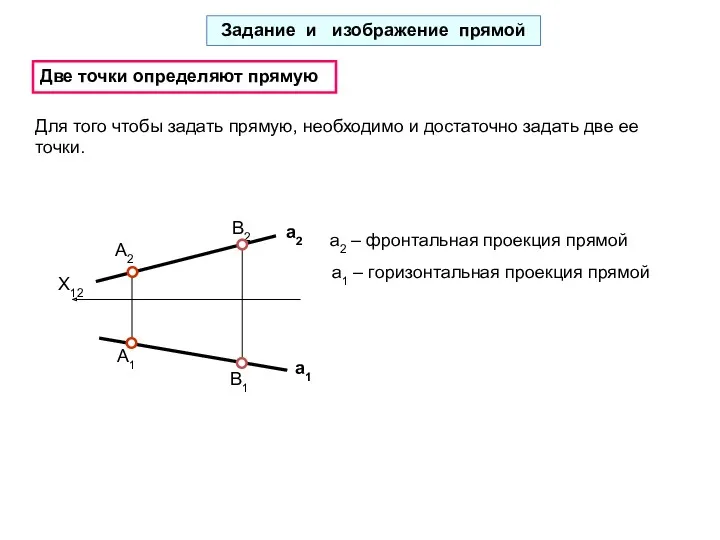
В1
В2
А1
Две точки определяют прямую
А2
X12
Для того чтобы задать прямую, необходимо и достаточно задать две ее точки.
а2
а1
Задание и изображение прямой
а2 – фронтальная проекция прямой
а1 – горизонтальная проекция прямой

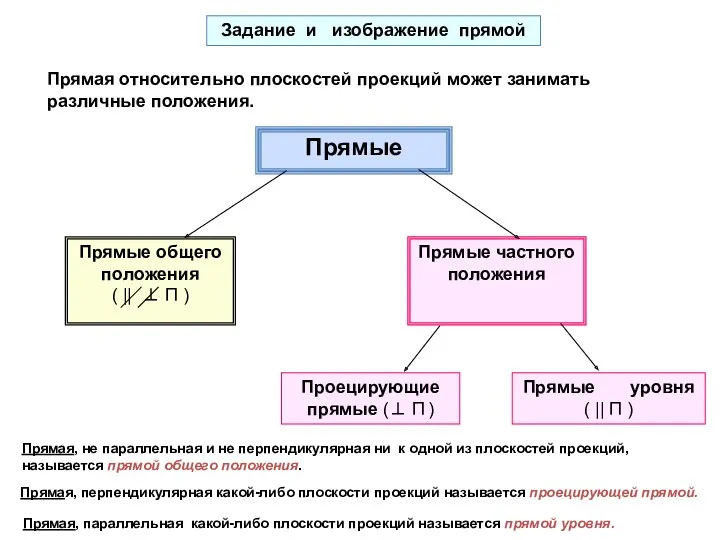
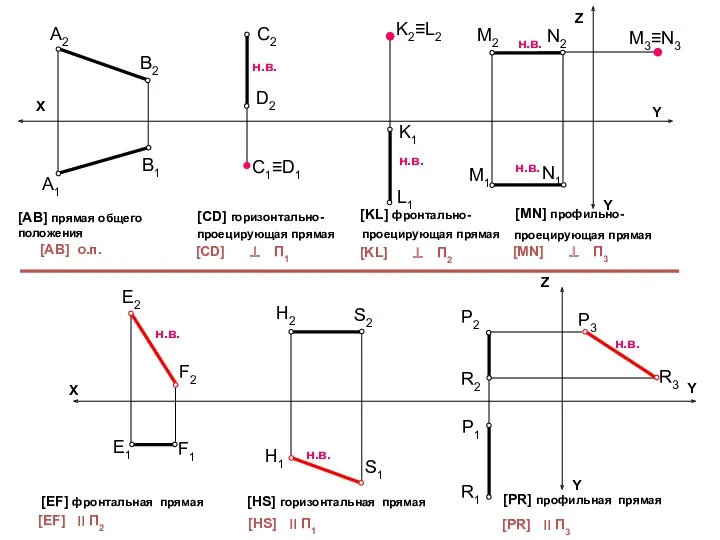
Прямые
Прямые частного положения
Проецирующие прямые (⊥ П )
Прямые уровня ( || П )
Задание и изображение прямой
Прямая относительно плоскостей проекций может занимать различные положения.
Прямая, не параллельная и не перпендикулярная ни к одной из плоскостей проекций, называется прямой общего положения.
Прямая, перпендикулярная какой-либо плоскости проекций называется проецирующей прямой.
Прямая, параллельная какой-либо плоскости проекций называется прямой уровня.

E1
C1≡D1
Х
Z
Y
A2
Y
Х
Y
Z
Y
В2
В1
A1
С2
D2
K1
L1
K2≡L2
M2
N2
M1
N1
M3≡N3
E2
F2
F1
H2
S2
H1
S1
P2
R2
P1
R1
P3
R3
[АВ] прямая общего положения
[АВ] о.п.
[CD] горизонтально-
проецирующая прямая
[СD] ⊥ П1 [KL] фронтально-
проецирующая прямая
[KL] ⊥ П2
[MN] профильно-
проецирующая прямая
[MN] ⊥ П3
[EF] фронтальная прямая
[HS] горизонтальная прямая
[PR] профильная прямая
[EF] ׀׀ П2
[HS] ׀׀ П1
[PR] ׀׀ П3
н.в.
н.в.
н.в.
н.в.
н.в.
н.в.
н.в.

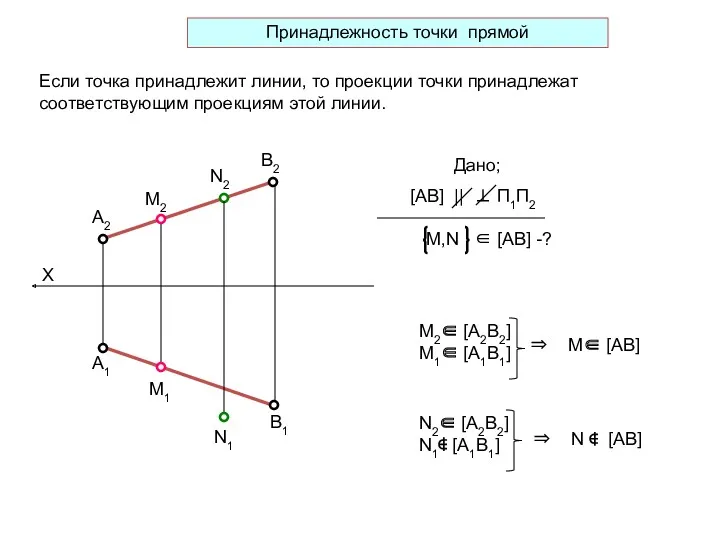
А2
В2
А1
В1
М2
N2
N1
М1
Дано;
М2∈ [А2B2]
М1∈ [А1B1]
⇒ М∈ [АB]
N2∈ [А2B2]
N1∉ [А1B1]
⇒ N ∉ [АB]
Принадлежность точки прямой
Если точка принадлежит линии, то проекции точки принадлежат соответствующим проекциям этой линии.

В2
K1
Взаимное положение прямых в пространстве
А2
А1
В1
С2
D2
С1
D1
M2
M1
K2
L2
L1
S2
T2
T1
S1
G2
V2
G1
V1
E2
H2
E1
H1
M2
N1
Параллельные прямые
Пересекающиеся прямые
Скрещивающиеся прямые
Одноименные проекции параллельных прямых всегда параллельны
[KL] || [ST]
Проекции точки пересечения прямых всегда находятся на одной линии связи
[СD] ∩ [AB] = M
Проекции точек пересечения проекций прямых никогда не находятся на одной линии связи
прямые, лежащие в одной плоскости и не имеющие общих точек
прямые, лежащие в одной плоскости и имеющие общую точку пересечения
прямые, не лежащие в одной плоскости

П Л О С К О С Т И
Плоскость
общего положения
Плоскость
частного положения
Плоскость уровня
Проецирующая
плоскость

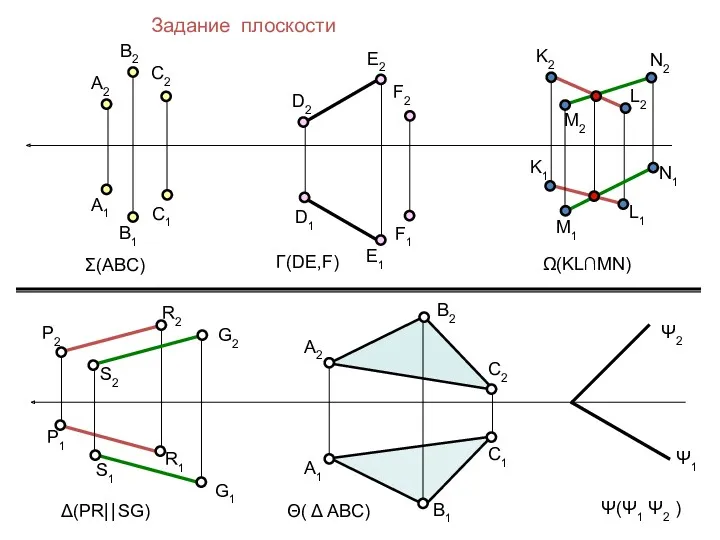
А2
В2
С2
А1
В1
С1
D2
E2
D1
E1
F2
F1
K2
L2
K1
L1
M2
N2
N1
M1
P2
R2
P1
R1
S1
S2
G2
G1
Σ(ABC)
Γ(DE,F)
Ω(KL∩MN)
Δ(PR⎢⎢SG)
А2
В2
С2
А1
В1
С1
Θ( Δ ABC)
Ψ(Ψ1 Ψ2 )
Задание плоскости
Ψ2
Ψ1

Θ( Δ ABC)- о.п.
Ω(а ∩ b) || П1
Σ(Δ DEF) || П2
Ψ(c ∩ d) || П3
F2
F1
c3
Φ ( m ∩ n) ⊥П2
Σ(Δ KLM) ⊥ П1
Γ(p || s) ⊥ П3
Фронтально-проецирующая плоскость
Горизонтально- проецирующая плоскость
Профильно-проецирующая плоскость
Плоскость о.п.
Горизонтальная плоскость
Фронтальная плоскость
Профильная плоскость

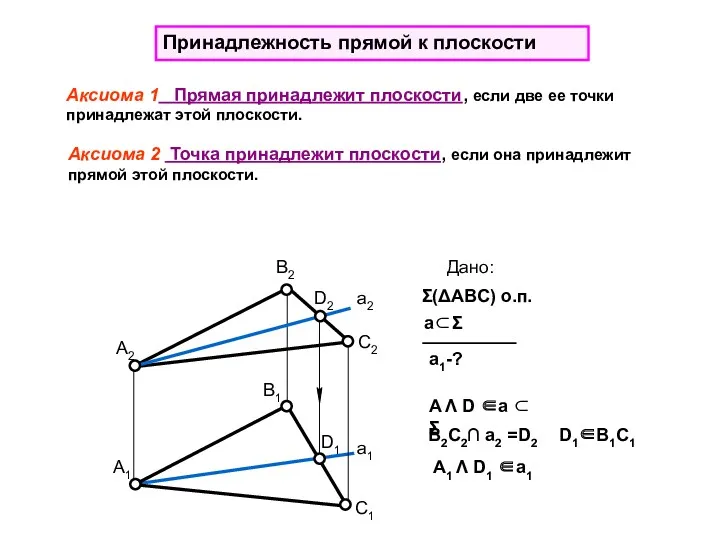
a1-?
a⊂Σ
В1
Принадлежность прямой к плоскости
Аксиома 1 Прямая принадлежит плоскости, если две ее точки принадлежат этой плоскости.
D2
А2
В2
С2
С1
А1
D1
D1∈B1C1
Дано:
Σ(ΔАВС) о.п.
a2
a1
Аксиома 2 Точка принадлежит плоскости, если она принадлежит прямой этой плоскости.
A Λ D ∈a ⊂ Σ
В2С2∩ a2 =D2
A1 Λ D1 ∈a1

11
Главные линии плоскости – горизонталь и фронталь
Горизонталью плоскости называется прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций П1
h II П1
h2
h1
12
f1
f2
Фронталью плоскости называется прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций П2
f II П2
X12

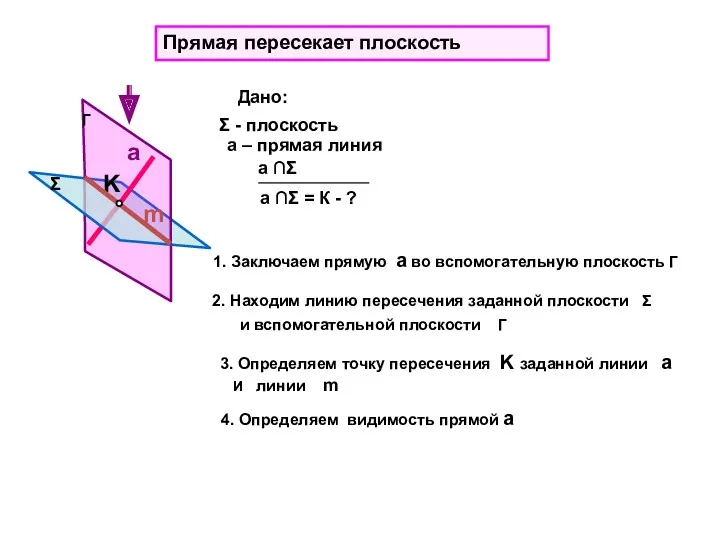
а ∩Σ = К - ?
Прямая пересекает плоскость
Σ
Г
K
a
m
1. Заключаем прямую а во вспомогательную плоскость Г
2. Находим линию пересечения заданной плоскости Σ
и вспомогательной плоскости Г
3. Определяем точку пересечения K заданной линии а
И линии m
4. Определяем видимость прямой а
Дано:
Σ - плоскость
а – прямая линия
а ∩Σ

K1
Прямая пересекает плоскость
а2
а1
m2
K2
12
22
21
11
m1
1. а ⊂ Г
Г ⊥ П2
2. Г ∩Σ = m
3. m ∩ a = K
m ⊂ Σ ⇒
a∩Σ = K
Дано:
Σ(ΔАВС)- о.п.
a – о.п.
a∩Σ=?

11
31
K1
Прямая пересекает плоскость
а2
а1
K2
12
≡ 32
Видимость прямой а на фронтальной проекции определяем фронтально конкурирующими точками.
Дано:
Σ(ΔАВС)- о.п.
a – о.п.
a∩Σ=?

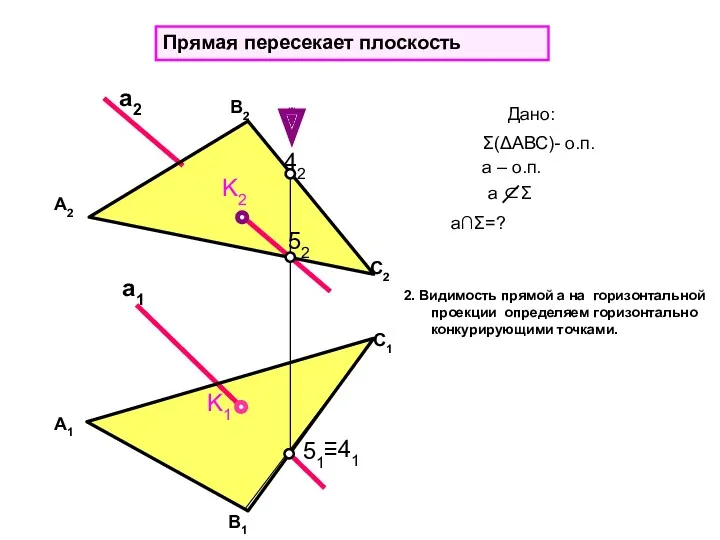
52
K1
Прямая пересекает плоскость
а2
а1
K2
42
≡41
51
2. Видимость прямой а на горизонтальной проекции определяем горизонтально конкурирующими точками.
Дано:
Σ(ΔАВС)- о.п.
a – о.п.
a∩Σ=?

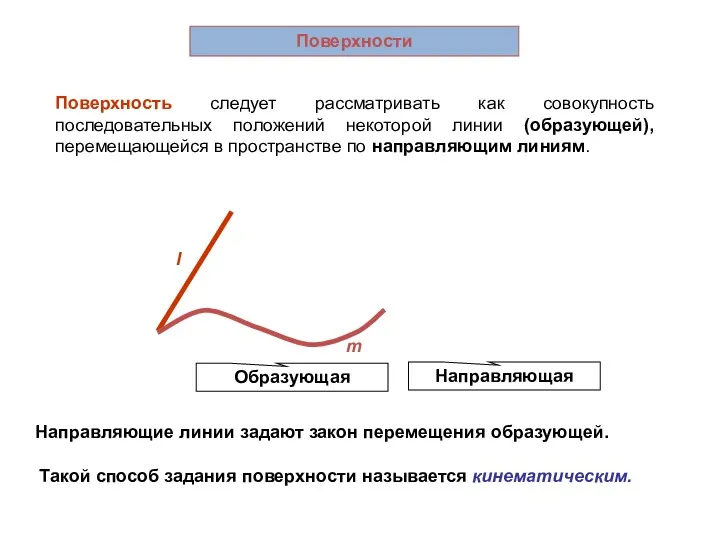
Направляющие линии задают закон перемещения образующей.
l
Образующая
Направляющая
m
Поверхность следует рассматривать как совокупность последовательных положений некоторой линии (образующей), перемещающейся в пространстве по направляющим линиям.
Поверхности
Такой способ задания поверхности называется кинематическим.

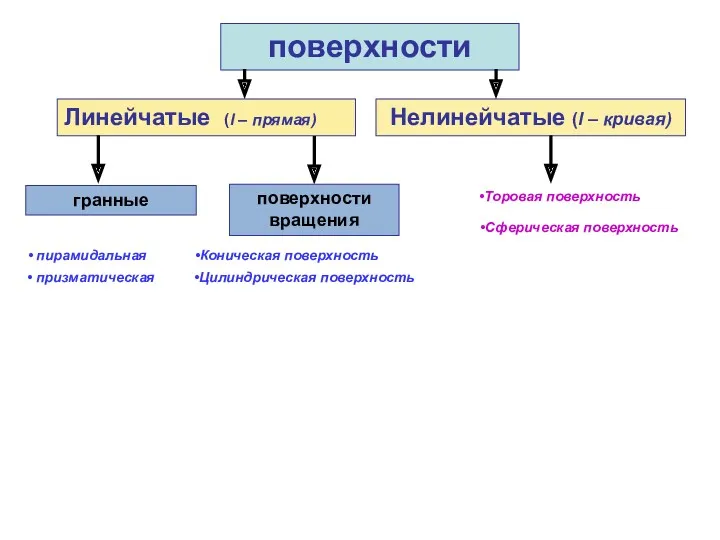
поверхности
Линейчатые (l – прямая)
Нелинейчатые (l – кривая)
гранные
поверхности вращения
пирамидальная
призматическая
Коническая поверхность
Цилиндрическая поверхность
Торовая поверхность
Сферическая поверхность

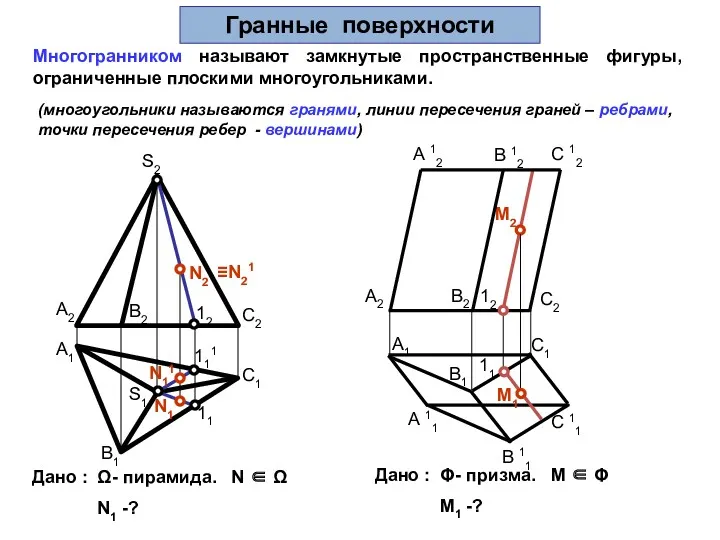
Гранные поверхности
Пирамидальная поверхность – это линейчатая поверхность, образованная перемещением прямой линии, проходящей через фиксированную точку S (вершину), по ломанной направляющей m
S
Призматическая поверхность – это линейчатая поверхность, образованная перемещением прямой линии, движущейся параллельно некоторому заданному направлению s и пересекающей направляющую m, которая представляет собой ломаную линию.
Г(m, S) [ l ∩ m, S∈l ]
Σ (m, s) [ l ∩ m, l ||s]
m
m
l
l

11
Многогранником называют замкнутые пространственные фигуры, ограниченные плоскими многоугольниками.
S2
S1
N2
N1
N11
M2
Дано : Ω- пирамида. N ∈ Ω
N1 -?
Дано : Φ- призма. M ∈ Φ
M1 -?
≡N21
M1
А2
B2
C2
C1
B1
А1
12
111
12
11
Гранные поверхности
(многоугольники называются гранями, линии пересечения граней – ребрами, точки пересечения ребер - вершинами)

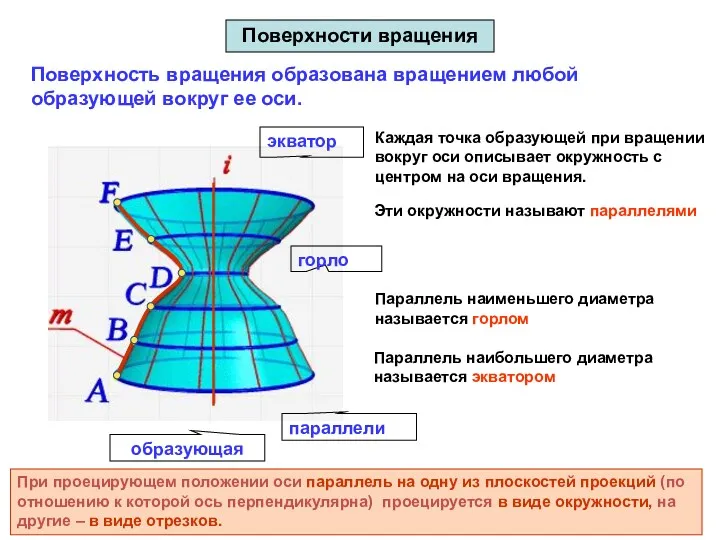
A
B
C
D
E
F
i
Каждая точка образующей при вращении вокруг оси описывает окружность с центром на оси вращения.
Эти окружности называют параллелями
Параллель наименьшего диаметра называется горлом
Параллель наибольшего диаметра называется экватором
Поверхности вращения
Поверхность вращения образована вращением любой образующей вокруг ее оси.
образующая
параллели
горло
экватор
При проецирующем положении оси параллель на одну из плоскостей проекций (по отношению к которой ось перпендикулярна) проецируется в виде окружности, на другие – в виде отрезков.

Линия пересечения меридиональной плоскости с поверхностью вращения называется меридианом
Все меридианы одной поверхности вращения равны между собой
Очерковые меридианы называются главными
Поверхности вращения
меридиан
Главный фронтальный меридиан
Плоскость, проходящая через ось поверхности вращения называется меридиональной плоскостью
Меридиан, очерковый относительно фронтальной плоскости проекций называется главным фронтальным меридианом

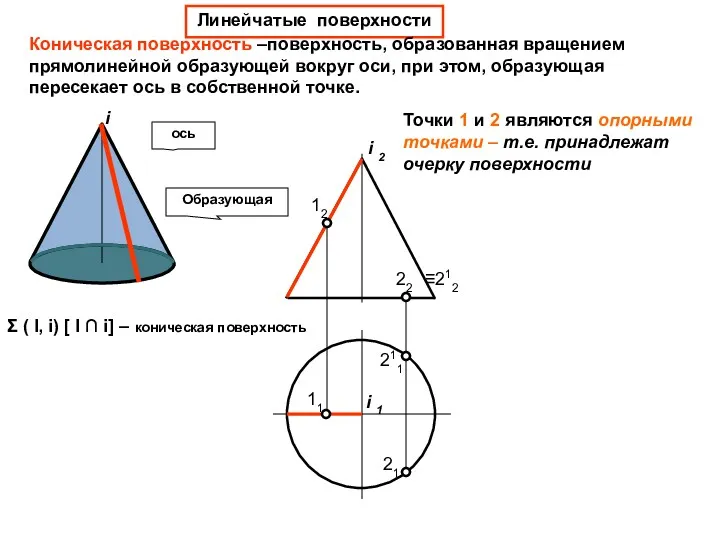
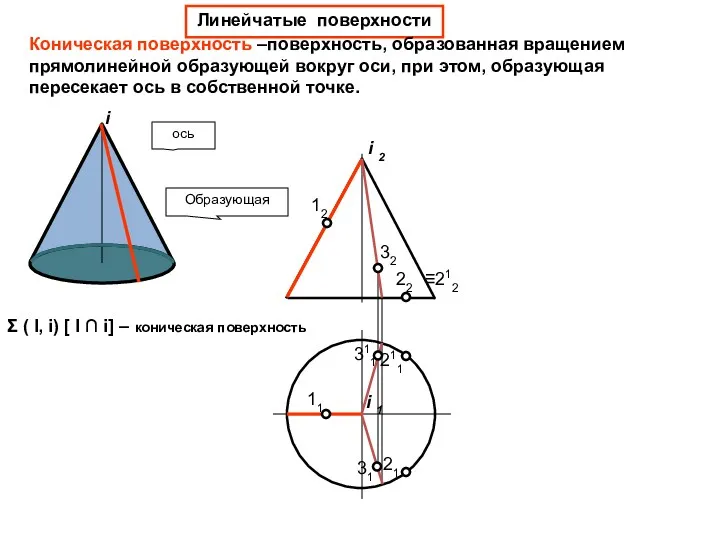
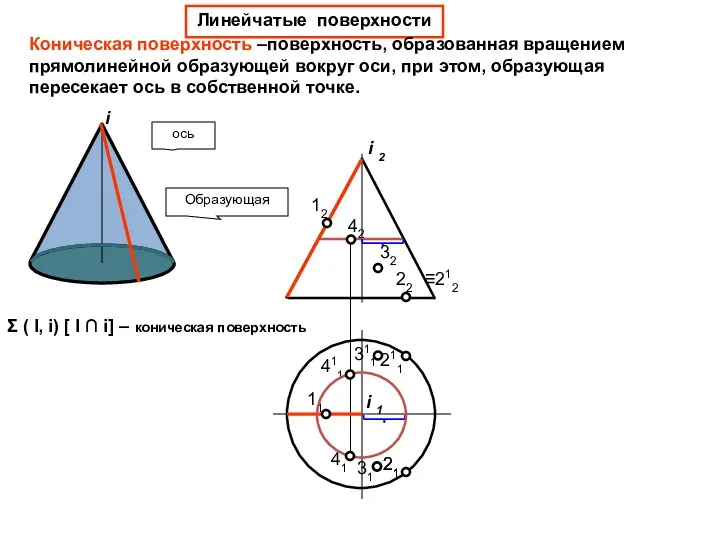
Линейчатые поверхности
Коническая поверхность –поверхность, образованная вращением прямолинейной образующей вокруг оси, при этом, образующая пересекает ось в собственной точке.
Σ ( l, i) [ l ∩ i] – коническая поверхность
12
11
22
211
21
i 2
i 1
≡212
i
Точки 1 и 2 являются опорными точками – т.е. принадлежат очерку поверхности
Образующая
ось

31
Образующая
ось
12
11
22
211
21
32
311
i 2
i 1
≡212
Линейчатые поверхности
Коническая поверхность –поверхность, образованная вращением прямолинейной образующей вокруг оси, при этом, образующая пересекает ось в собственной точке.
Σ ( l, i) [ l ∩ i] – коническая поверхность
i

411
41
31
Образующая
ось
12
11
22
211
21
32
311
42
21
i 2
i 1
≡212
Линейчатые поверхности
Коническая поверхность –поверхность, образованная вращением прямолинейной образующей вокруг оси, при этом, образующая пересекает ось в собственной точке.
Σ ( l, i) [ l ∩ i] – коническая поверхность
i

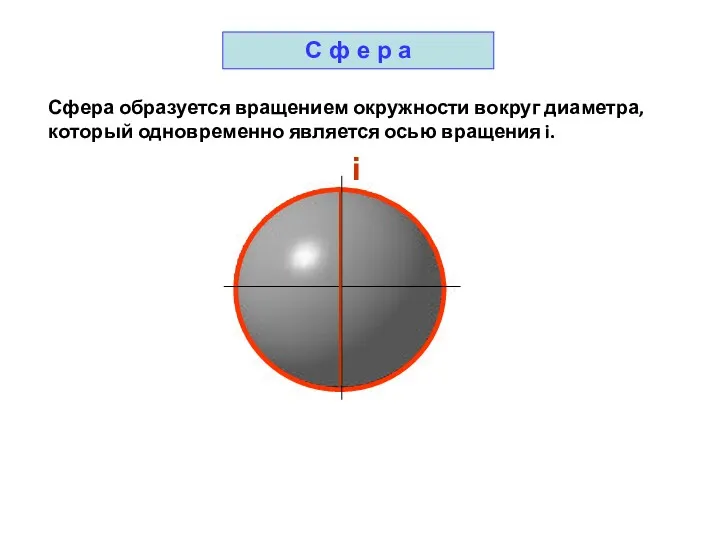
Сфера образуется вращением окружности вокруг диаметра, который одновременно является осью вращения i.
i
С ф е р а

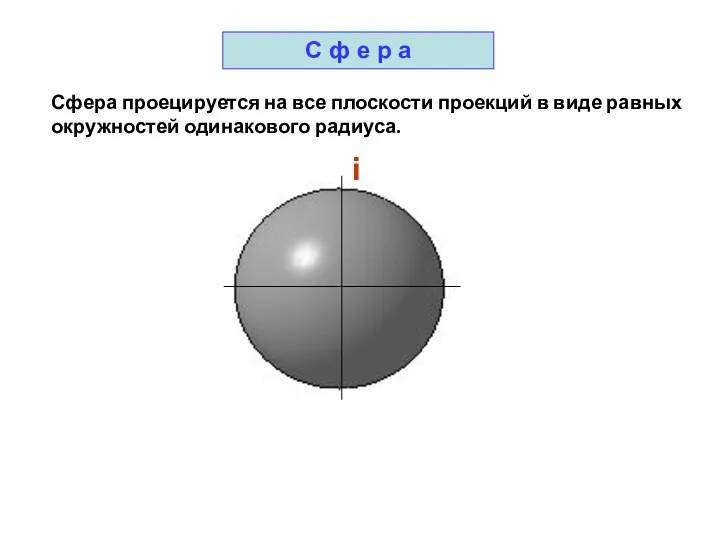
Сфера проецируется на все плоскости проекций в виде равных окружностей одинакового радиуса.
i
С ф е р а

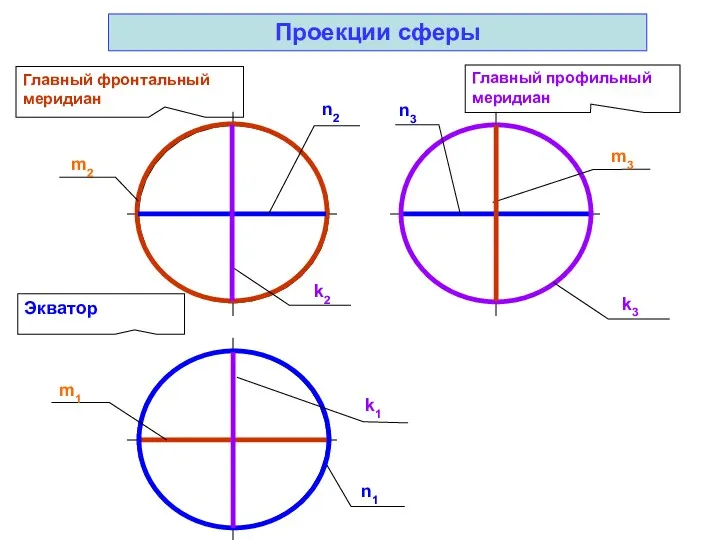
Проекции сферы
Главный фронтальный меридиан
Главный профильный меридиан
Экватор

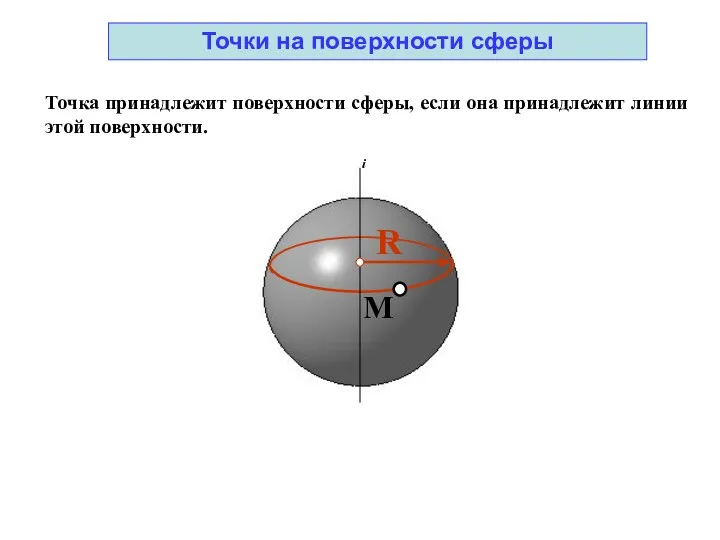
i
M
R
Точка принадлежит поверхности сферы, если она принадлежит линии этой поверхности.
Точки на поверхности сферы

Опорные точки на поверхности сферы
A1
A2
A3

D3
Опорные точки на поверхности сферы
D1I
D2
D1
≡D2I
D3I

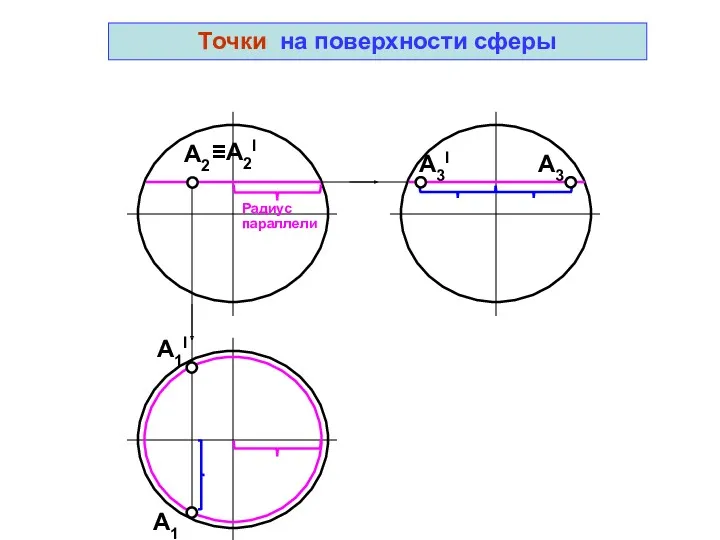
A1I
Точки на поверхности сферы
A2
A1
A3I
A3
Радиус
параллели
≡А2I

Конические сечения

Конус может иметь в сечении пять различных фигур:
1. Треугольник, если секущая плоскость пересекает конус, через вершину по двум образующим
2. Окружность, если секущая плоскость параллельна основанию или перпендикулярна оси, а конус прямой круговой
3. Эллипс, если секущая плоскость пересекает все образующие конуса под некоторым углом к основанию конуса.
4. Параболу, если секущая плоскость параллельна одной из образующих конуса
5. Гиперболу, если секущая плоскость параллельна оси конуса или параллельна двум его образующим

12
Дано:
- конус
Σ- плоскость
Σ∩Γ = m
Σ2
11I
11
m - треугольник
Две образующие(треугольник)
Σ

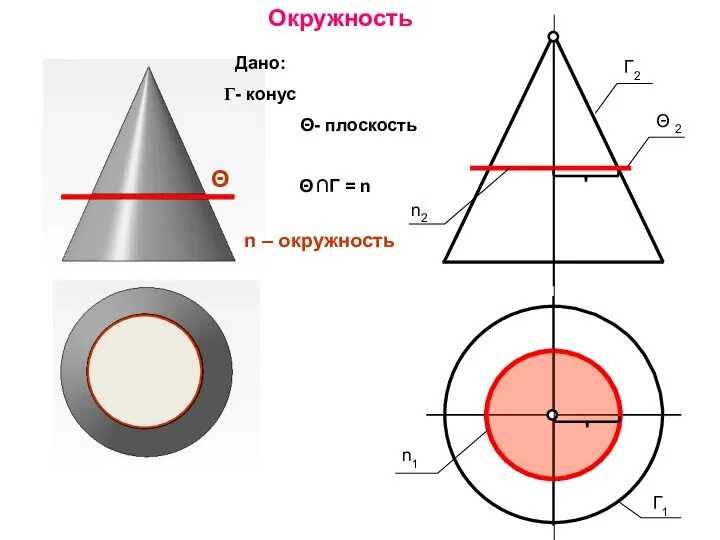
Окружность
Дано:
- конус
Θ- плоскость
Θ ∩Γ = n
n1
n – окружность
Θ

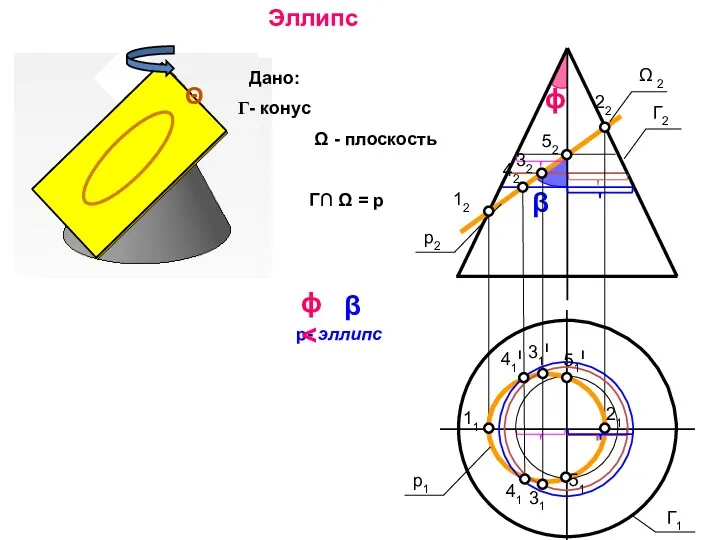
11
12
22
21
32
31
31I
42
41I
41
52
51I
51
Эллипс
Θ
Дано:
- конус
Ω - плоскость
Γ∩ Ω = p

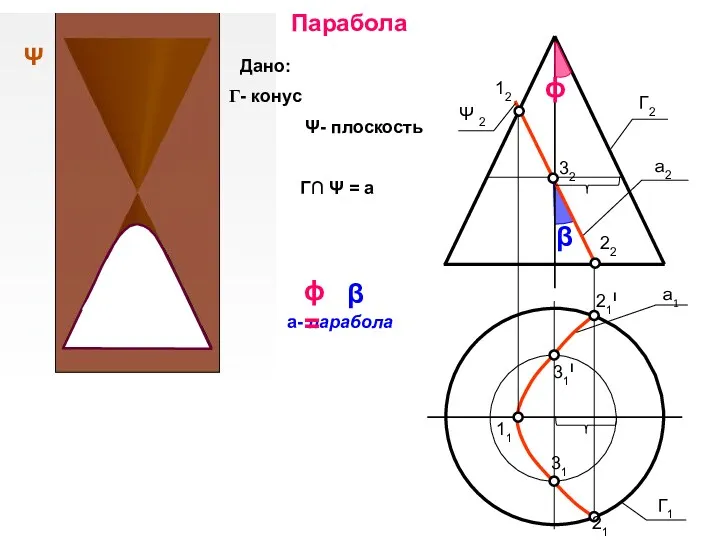
Дано:
- конус
Ψ- плоскость
Γ∩ Ψ = а
11
12
22
21I
21
32
31
31I
Парабола
Ψ

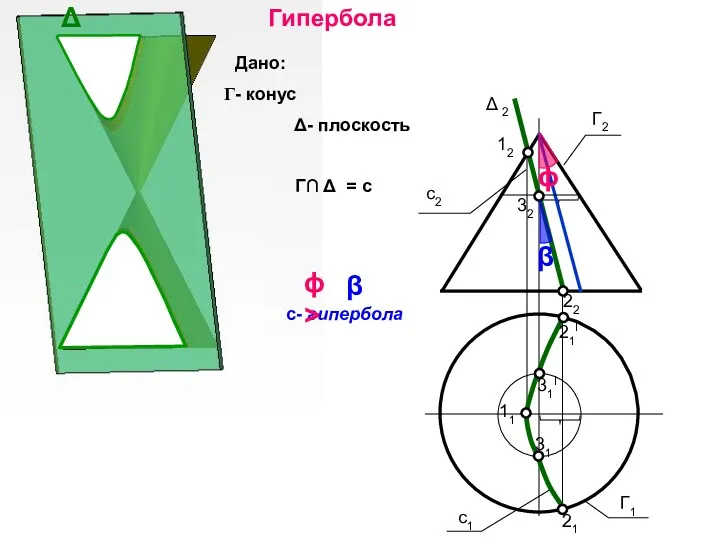
32
21
Δ 2
12
22
21I
31I
31
11
Гипербола
Δ
Дано:
- конус
Δ- плоскость
Γ∩ Δ = с

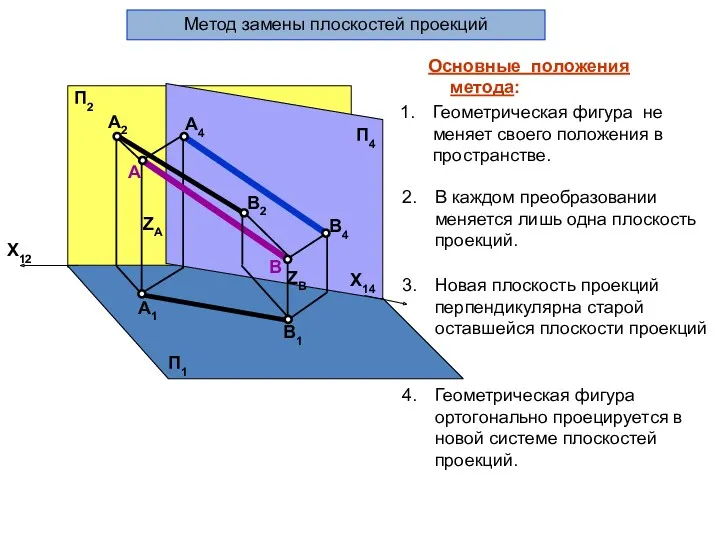
А
B
А1
B1
B4
А4
А2
B2
ZA
ZB
П1
П2
П4
Метод замены плоскостей проекций
Основные положения метода:
Геометрическая фигура не меняет своего положения в пространстве.
В каждом преобразовании меняется лишь одна плоскость проекций.
Новая плоскость проекций перпендикулярна старой оставшейся плоскости проекций
Геометрическая фигура ортогонально проецируется в новой системе плоскостей проекций.
X12
X14

α
X12
П2
П1
П1
П4
X14
А2
B2
B1
А1
B4
А4
Дано:
[AB] – о.п.
[AB] || П
П2 →П4 ⊥ П1 П4 || [AB]
1 задача. Комплексный чертеж преобразовать так, чтобы прямая общего положения стала прямой уровня.
X12 →X14|| [A1B1]
X14= П4 ∩ П1

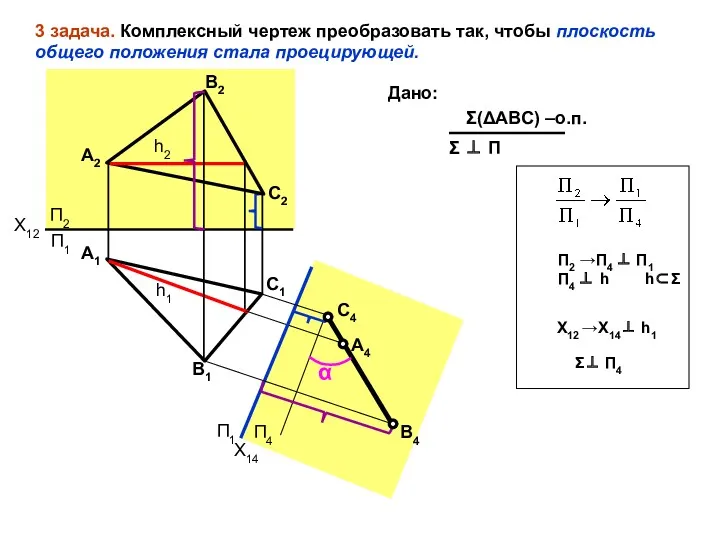
П2 →П4 ⊥ П1
П4 ⊥ [AB]
X12 →X14⊥ [A1B1]
2 задача. Комплексный чертеж преобразовать так, чтобы прямая уровня стала проецирующей прямой.
П2
П1
П1
П4
X14
А2
B2
B1
А1
А4 ≡ B4
X12

П2
П1
А2
А1
X12
B2
B1
С1
С2
С4
B4
А4
X14
П4
П1
Дано:
Σ(ΔАВС) –о.п.
Σ ⊥ П
h2
h1
α
П2 →П4 ⊥ П1
П4 ⊥ h h⊂Σ
X12 →X14⊥ h1
Σ⊥ П4
3 задача. Комплексный чертеж преобразовать так, чтобы плоскость общего положения стала проецирующей.

4 задача. Комплексный чертеж преобразовать так, чтобы проецирующая плоскость стала плоскостью уровня.
X12 →X14|| Σ1 (А1В1С1)
П2 →П4 ⊥ П1
П4 || Σ
П2
П1
А2
А1
B1
С1
С2
X14
П4
П1
B2
X12
А4
B4
С4
Дано:
Σ(ΔАВС) –о.п.
Σ II П

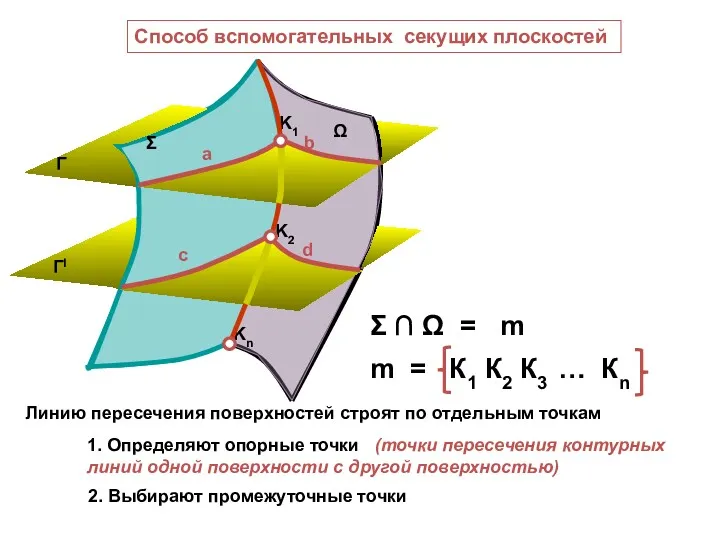
Способ вспомогательных секущих плоскостей
Σ
Ω
a
b
K1
K2
Kn
Σ ∩ Ω = m
с
d
Линию пересечения поверхностей строят по отдельным точкам
1. Определяют опорные точки (точки пересечения контурных линий одной поверхности с другой поверхностью)
2. Выбирают промежуточные точки
m = К1 К2 К3 … Кn

Секущие плоскости должны быть выбраны так, чтобы их линии пересечения с заданными поверхностями были бы простейшими (прямыми или окружностями)

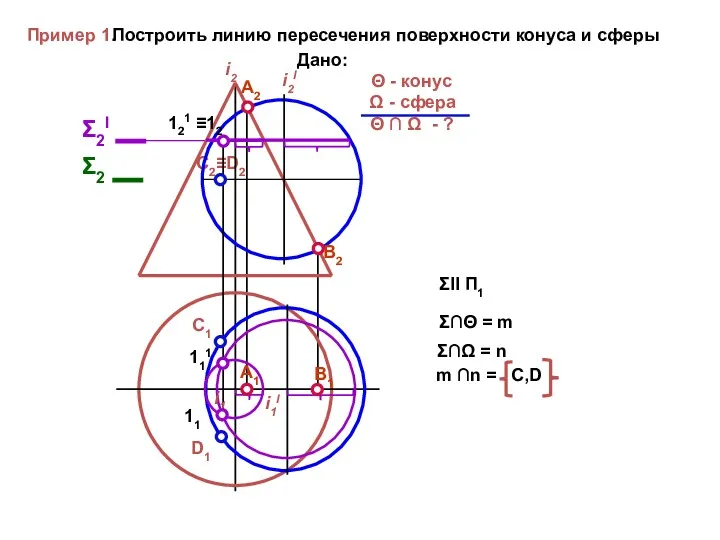
Пример 1.
Построить линию пересечения поверхности конуса и сферы
Дано:
Θ - конус
Ω - сфера
Θ ∩ Ω - ?

С2≡D2
D1
Пример 1.
Построить линию пересечения поверхности конуса и сферы
A2
B2
A1
B1
Σ2
C1
ΣII П1
Дано:
Θ - конус
Ω - сфера
Θ ∩ Ω - ?
m1
n1
m2
n2
Σ∩Θ = m
Σ∩Ω = n
m ∩n = C,D
i2
i1
i2I
i1I

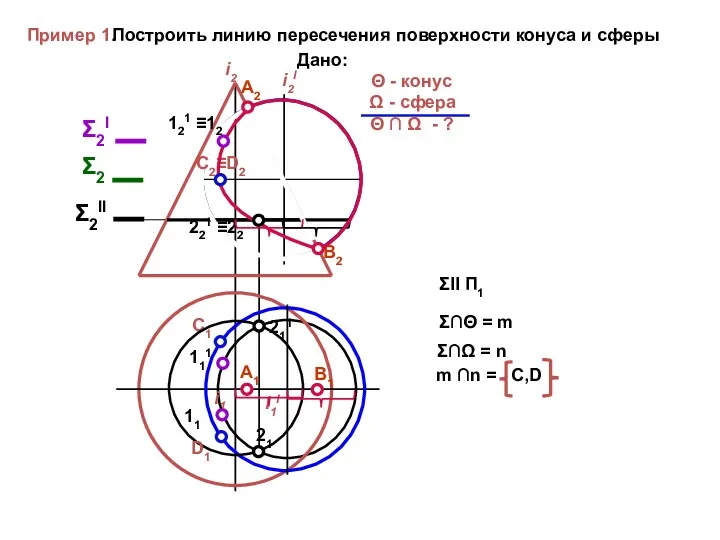
D1
C1
С2≡D2
Пример 1.
Построить линию пересечения поверхности конуса и сферы
A2
B2
A1
B1
Σ2
Σ2I
Дано:
Θ - конус
Ω - сфера
Θ ∩ Ω - ?
i2
i1
i2I
i1I
11
111
121 ≡12
ΣII П1
Σ∩Θ = m
Σ∩Ω = n
m ∩n = C,D

Пример 1.
Построить линию пересечения поверхности конуса и сферы
A2
B2
A1
B1
Σ2
C1
Σ2I
Σ2II
Дано:
Θ - конус
Ω - сфера
Θ ∩ Ω - ?
i2
i1
i2I
i1I
D1
11
111
121 ≡12
221 ≡22
211
21
С2≡D2
ΣII П1
Σ∩Θ = m
Σ∩Ω = n
m ∩n = C,D