Содержание
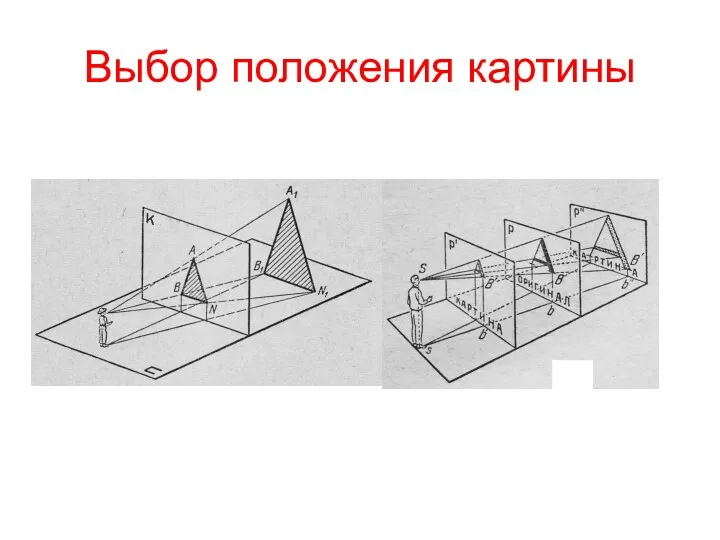
- 2. Выбор положения картины Картина может располагаться : перед объектом; проходить через ребро объекта; За объектом Угол
- 3. Выбор положения картины
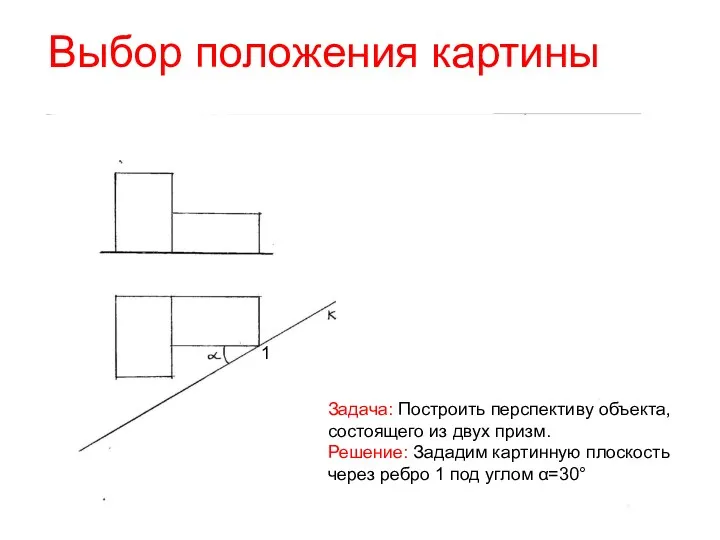
- 4. Выбор положения картины Задача: Построить перспективу объекта, состоящего из двух призм. Решение: Зададим картинную плоскость через
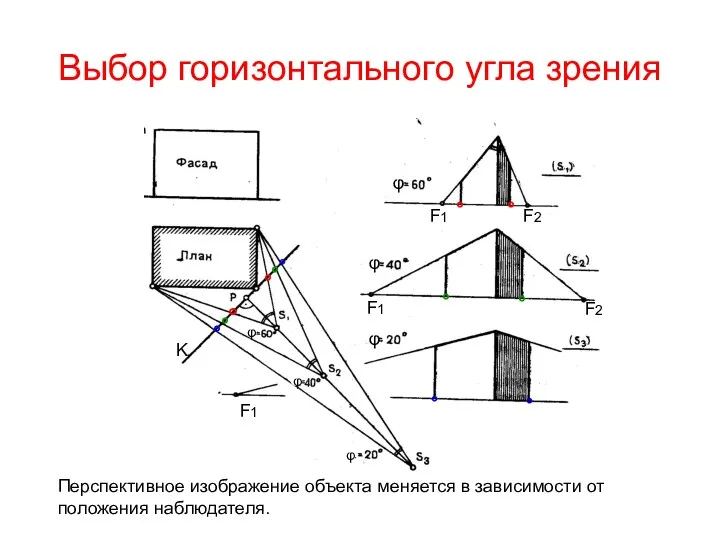
- 5. Выбор горизонтального угла зрения ° ° ° ° ° ° ° ° ° ° ° °
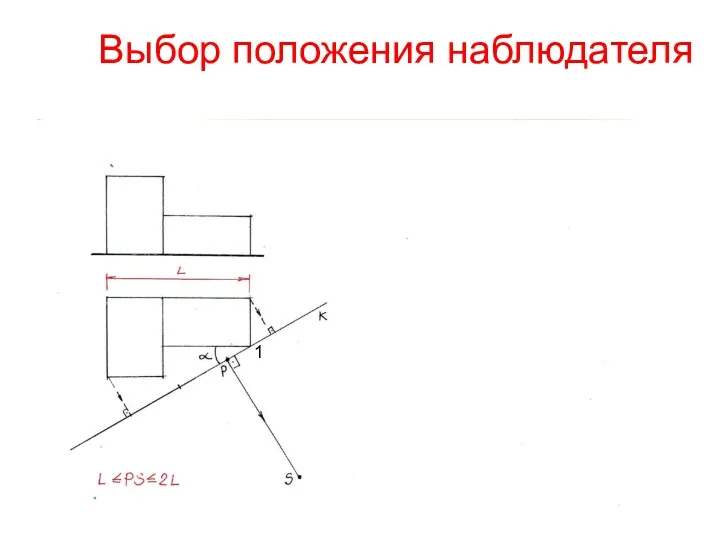
- 6. Выбор положения наблюдателя Угол зрения φ= от 20° до 60°. Данное значение получается, если дистанционное расстояние
- 7. Выбор положения наблюдателя 1
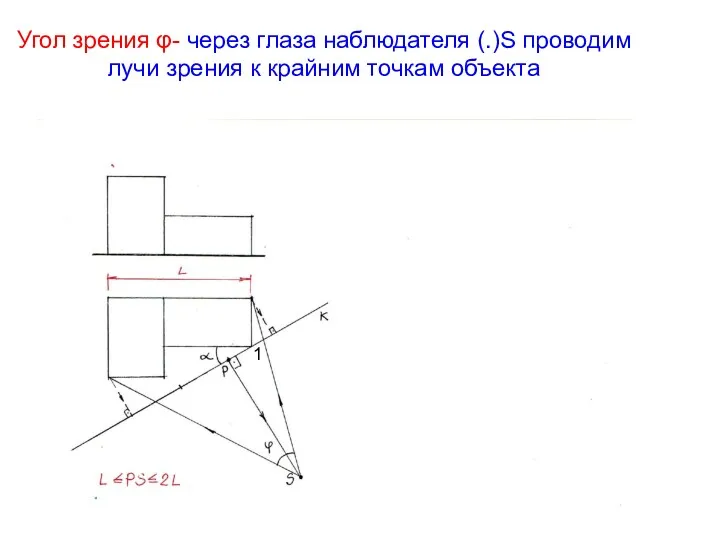
- 8. Угол зрения φ- через глаза наблюдателя (.)S проводим лучи зрения к крайним точкам объекта 1
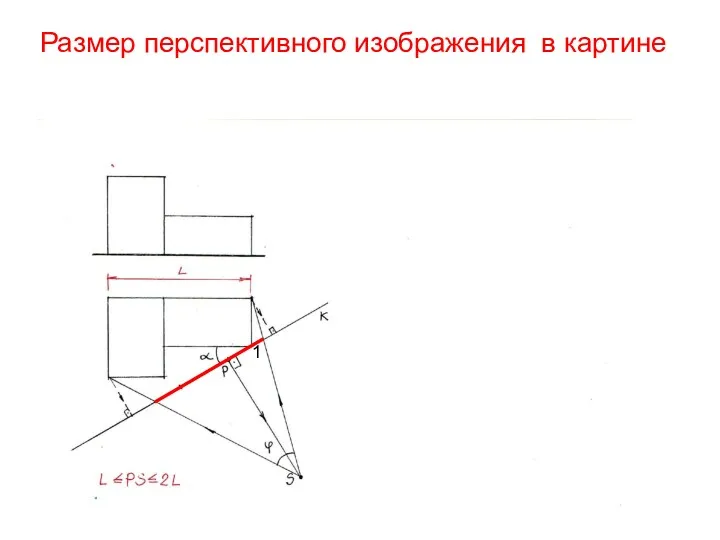
- 9. Размер перспективного изображения в картине 1
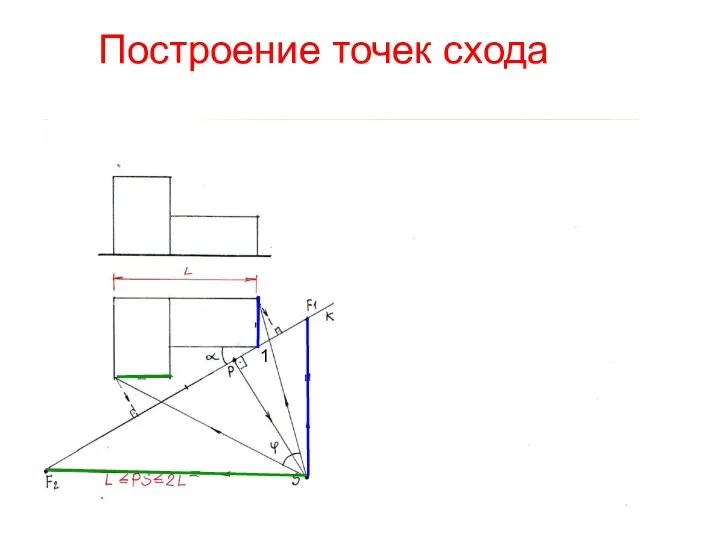
- 10. Построение точек схода прямых Чтобы построить точку схода любой прямой, необходимо через глаза наблюдателя (точку S)
- 11. Построение точек схода 1
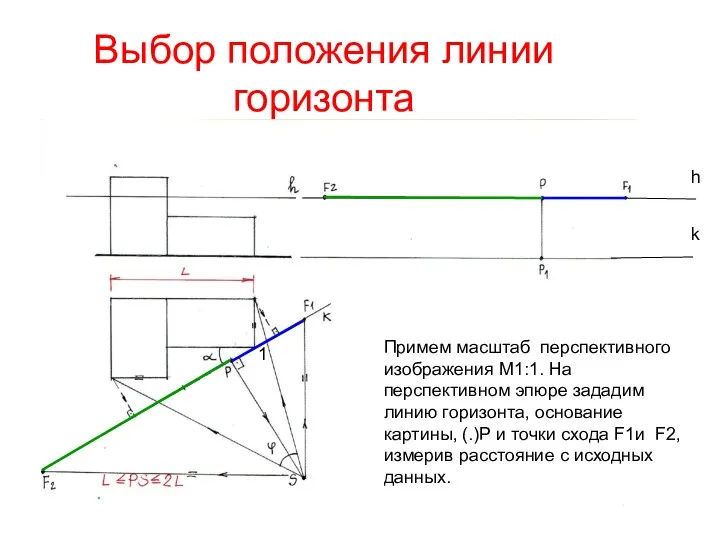
- 12. Выбор положения линии горизонта Линия горизонта может располагаться на любой высоте в зависимости от положения глаз
- 13. Выбор положения линии горизонта Примем масштаб перспективного изображения М1:1. На перспективном эпюре зададим линию горизонта, основание
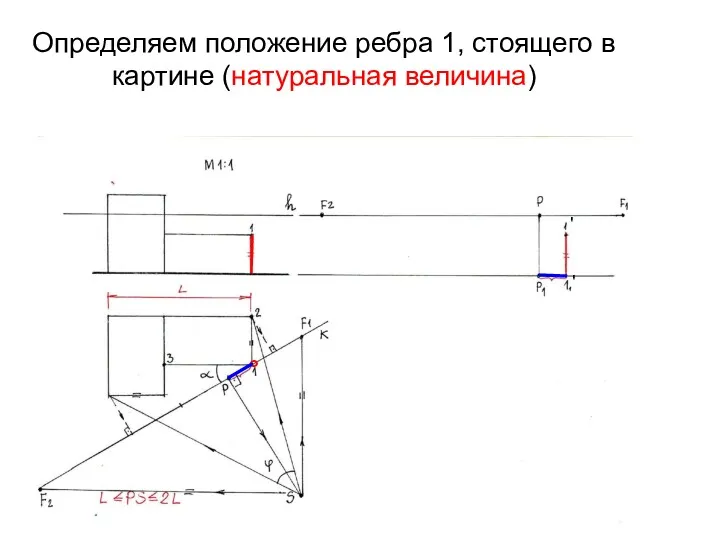
- 14. Определяем положение ребра 1, стоящего в картине (натуральная величина) ° ' '
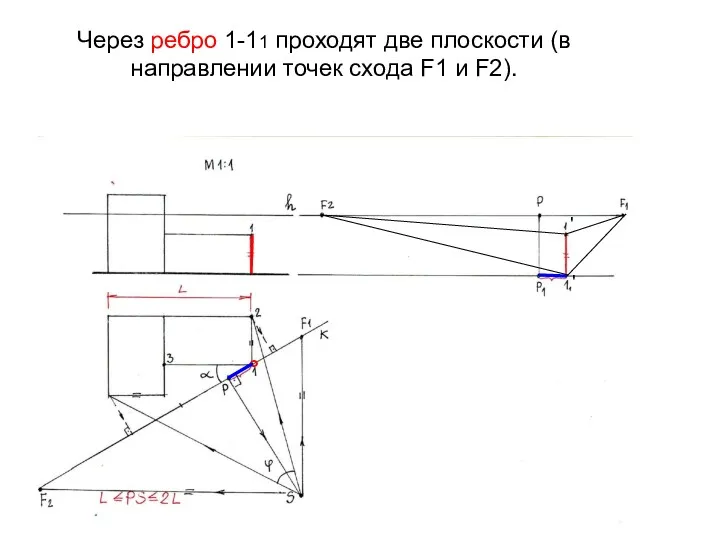
- 15. Через ребро 1-11 проходят две плоскости (в направлении точек схода F1 и F2). ° ' '
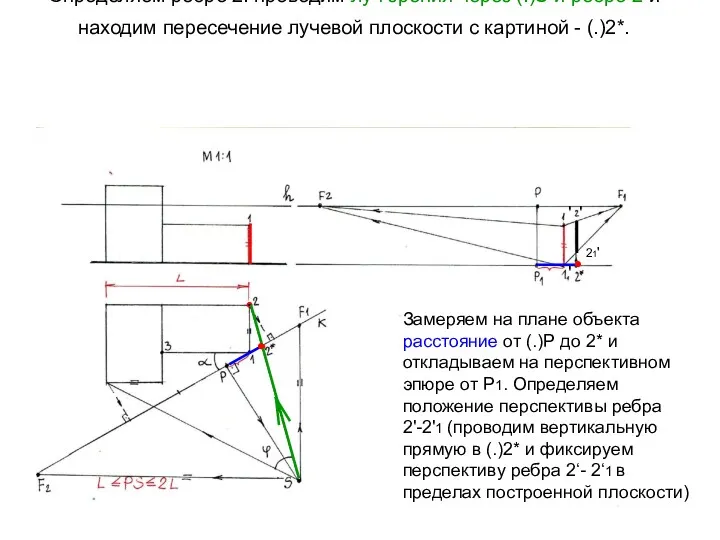
- 16. Определяем ребро 2: проводим луч зрения через (.)S и ребро 2 и находим пересечение лучевой плоскости
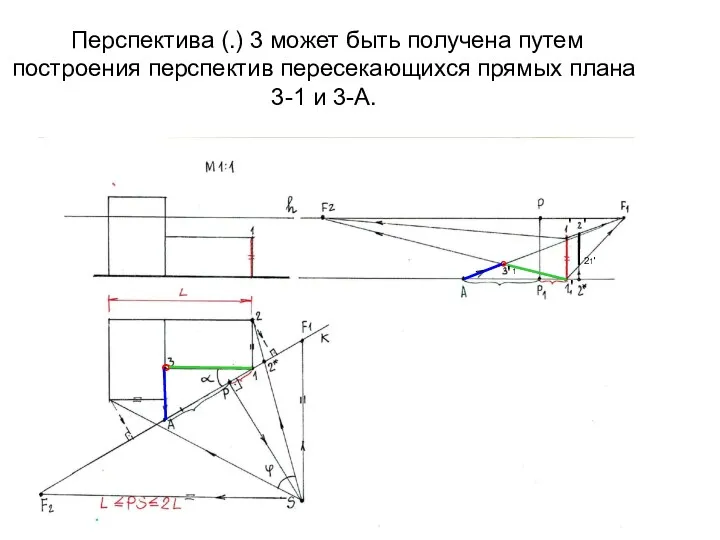
- 17. Перспектива (.) 3 может быть получена путем построения перспектив пересекающихся прямых плана 3-1 и 3-А. °
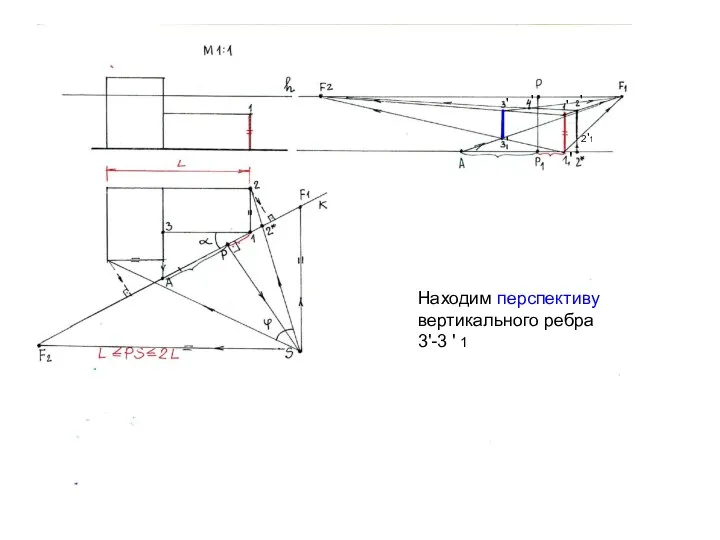
- 18. Находим перспективу вертикального ребра 3'-3 ' 1 ' ' ' ' ' ' 2'1
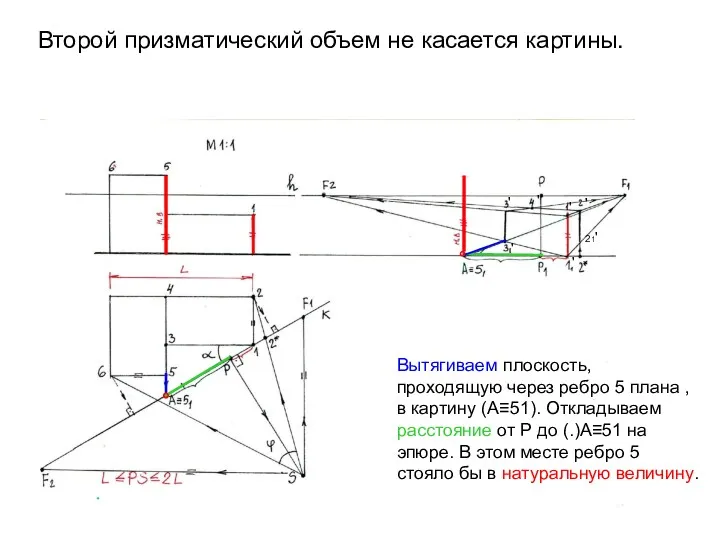
- 19. Второй призматический объем не касается картины. ° ° Вытягиваем плоскость, проходящую через ребро 5 плана ,
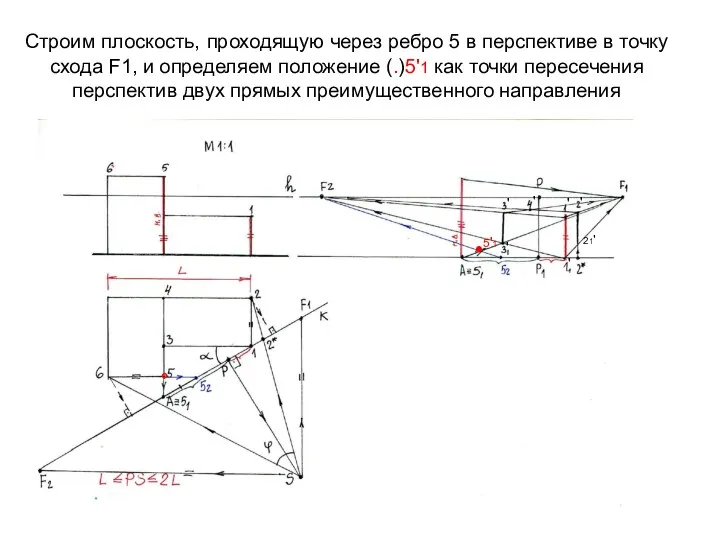
- 20. Строим плоскость, проходящую через ребро 5 в перспективе в точку схода F1, и определяем положение (.)5'1
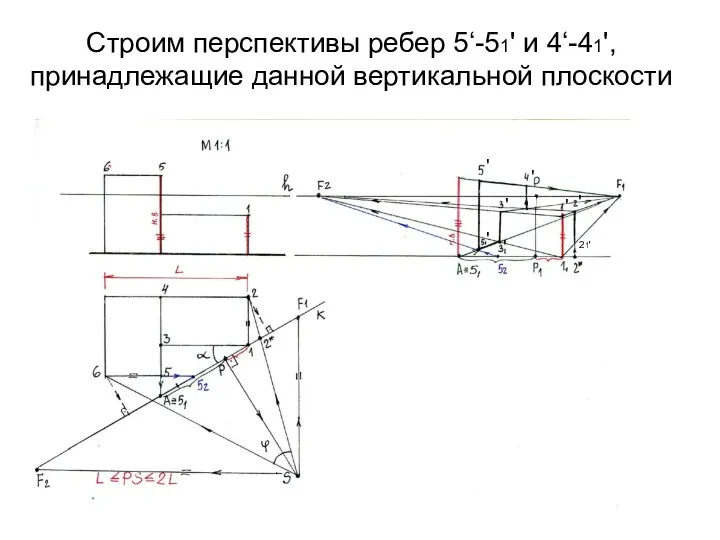
- 21. Строим перспективы ребер 5‘-51' и 4‘-41', принадлежащие данной вертикальной плоскости ' ' ' ' ' '
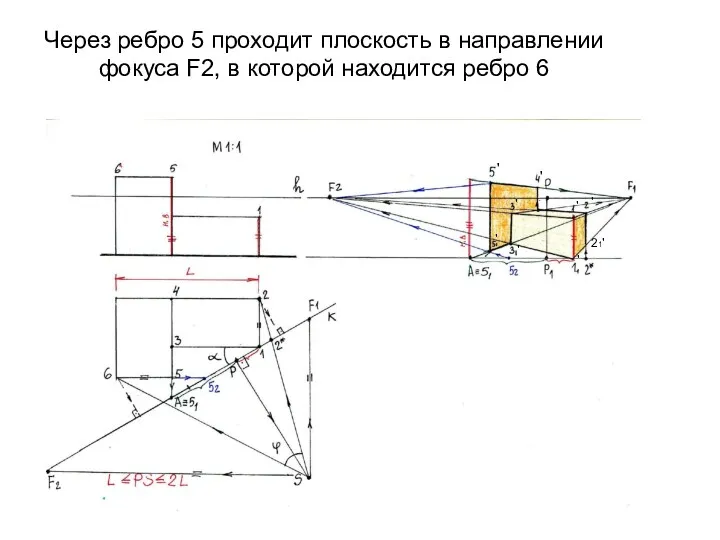
- 22. Через ребро 5 проходит плоскость в направлении фокуса F2, в которой находится ребро 6 ' '
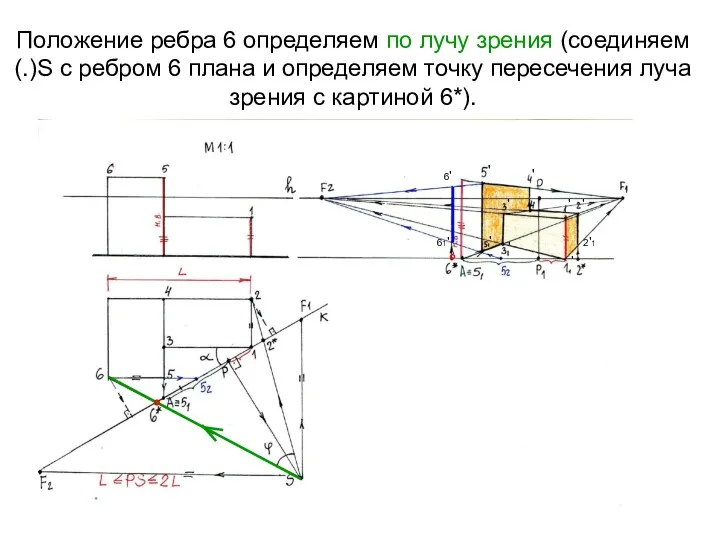
- 23. Положение ребра 6 определяем по лучу зрения (соединяем (.)S с ребром 6 плана и определяем точку
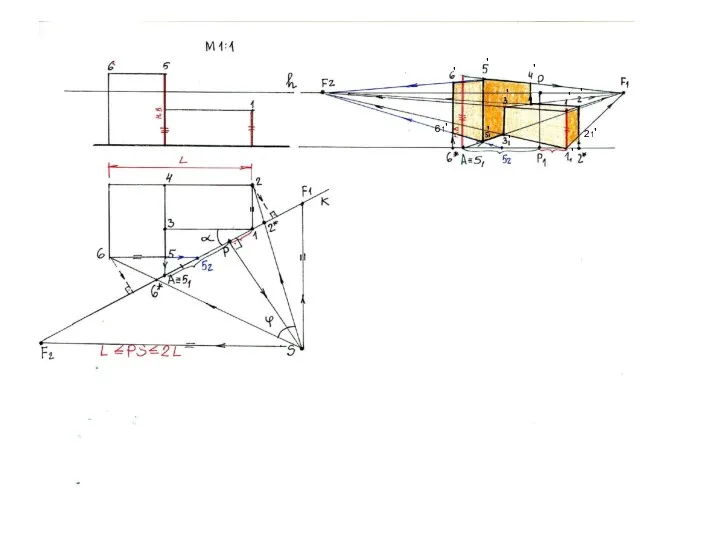
- 24. ' ' ' ' ' 61' ' ' ' ' 21'
- 25. Для построения перспективы объекта можно использовать разные приемы: Пеленговать точки объекта с помощью: прямых преимущественного направления
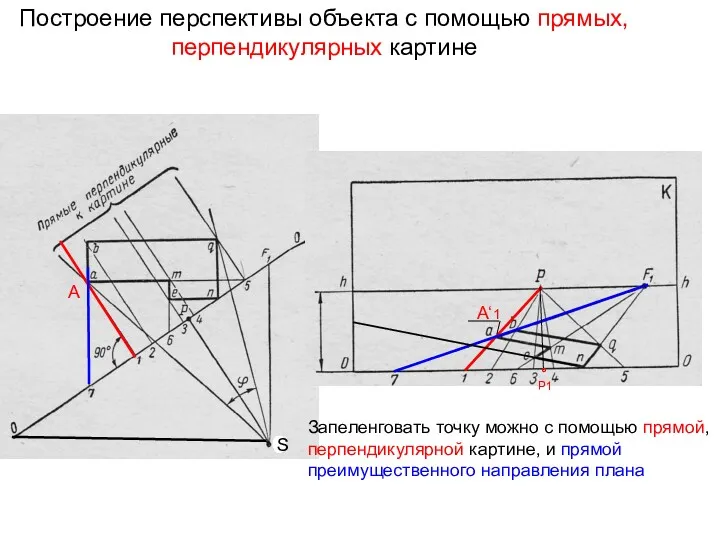
- 26. Построение перспективы объекта с помощью прямых, перпендикулярных картине А А‘1 Запеленговать точку можно с помощью прямой,
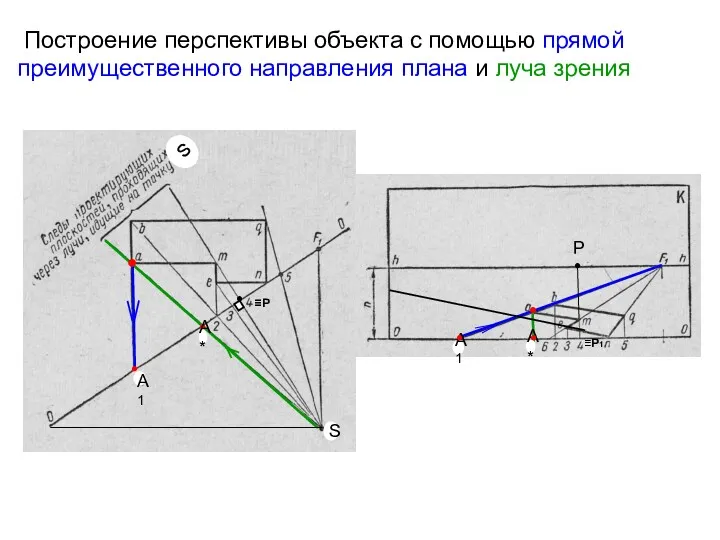
- 27. Построение перспективы объекта с помощью прямой преимущественного направления плана и луча зрения S ≡P P ≡P1
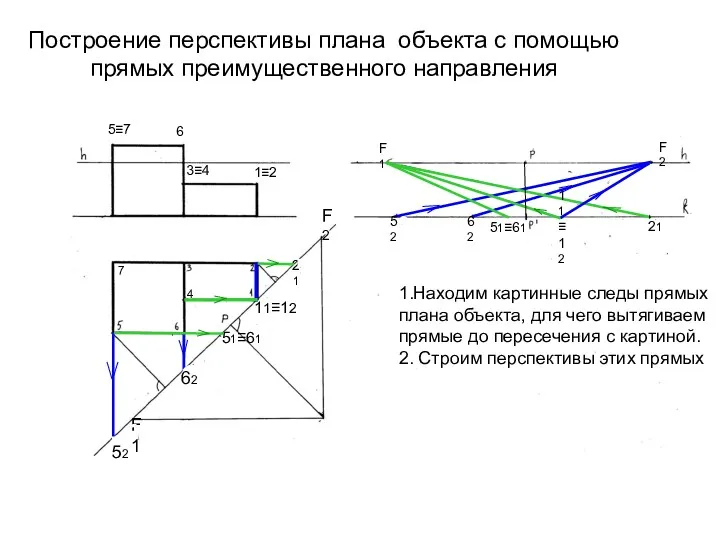
- 28. Построение перспективы плана объекта с помощью прямых преимущественного направления 1.Находим картинные следы прямых плана объекта, для
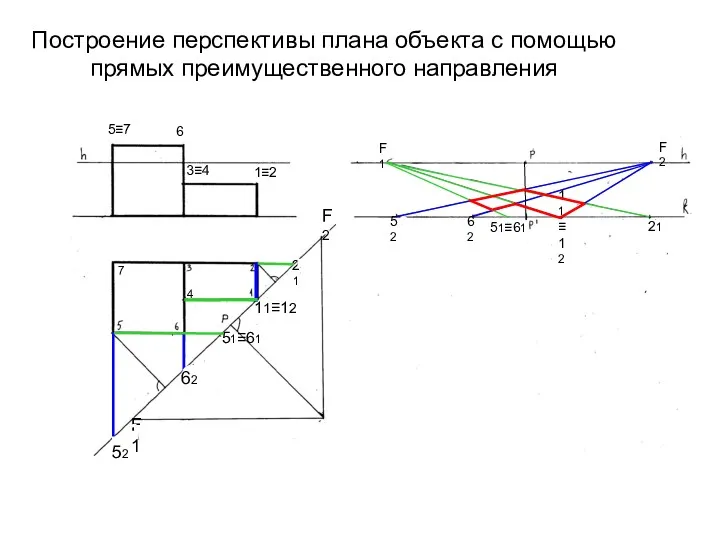
- 29. Построение перспективы плана объекта с помощью прямых преимущественного направления 52 62 21 4 52 62 11≡12
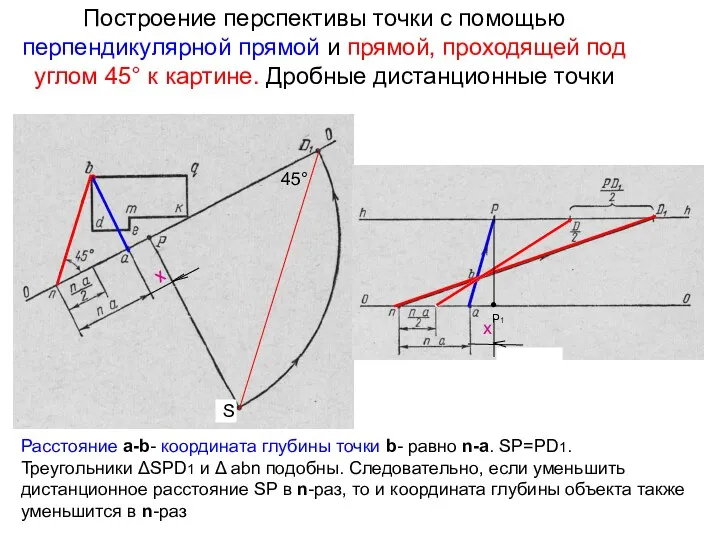
- 30. Построение перспективы точки с помощью перпендикулярной прямой и прямой, проходящей под углом 45° к картине. Дробные
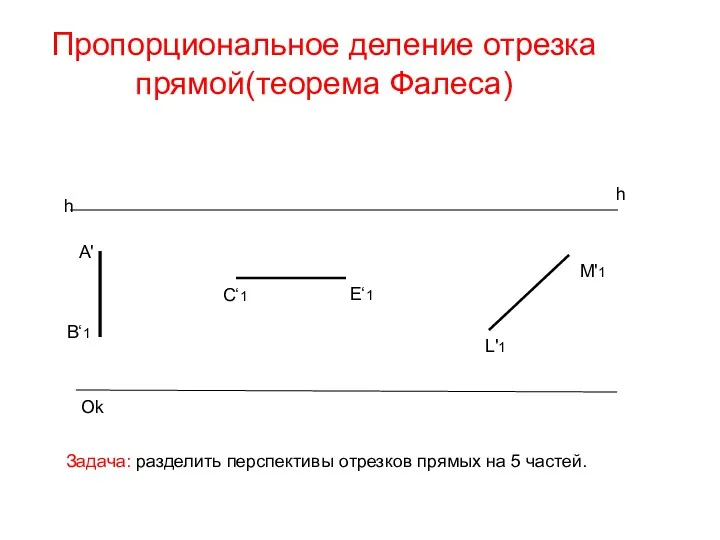
- 31. Пропорциональное деление отрезка прямой(теорема Фалеса) h h Ok A' B‘1 C‘1 E‘1 L'1 M'1 Задача: разделить
- 32. Пропорциональное деление отрезка прямой(теорема Фалеса) h h Ok A' B‘1 C‘1 E‘1 L'1 M'1 Через конец
- 33. Пропорциональное деление отрезка прямой(теорема Фалеса) h h Ok A' B‘1 C‘1 E‘1 L'1 M'1 В этом
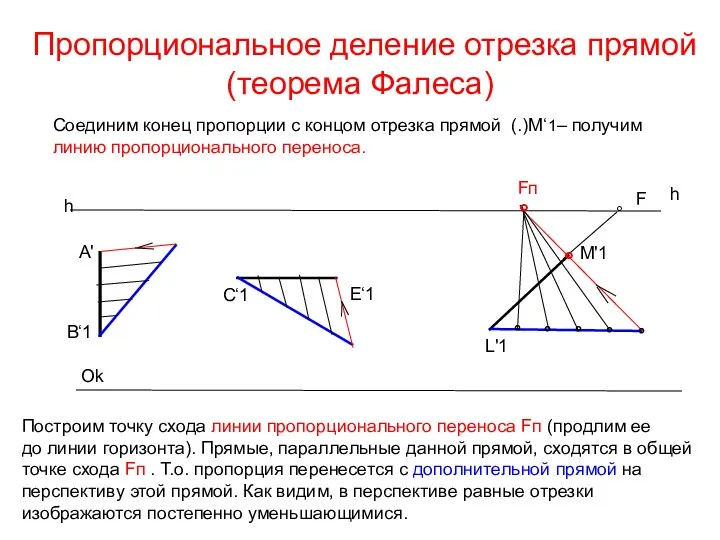
- 34. Пропорциональное деление отрезка прямой(теорема Фалеса) h h Ok A' B‘1 C‘1 E‘1 L'1 M'1 ° F
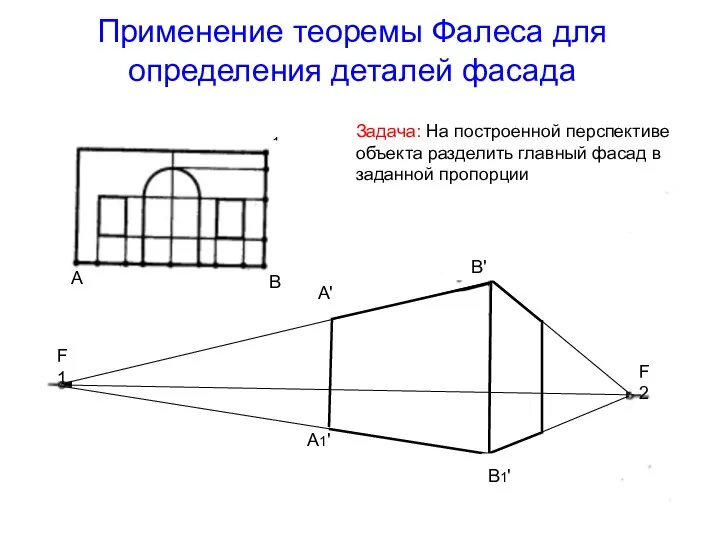
- 35. Применение теоремы Фалеса для определения деталей фасада Задача: На построенной перспективе объекта разделить главный фасад в
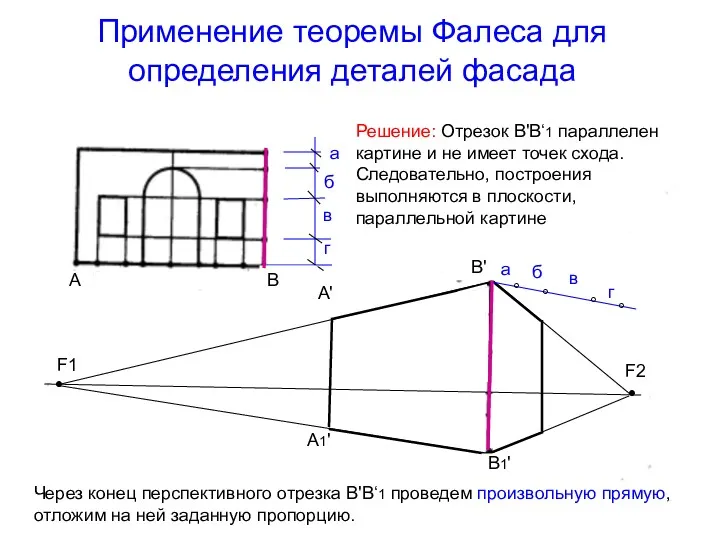
- 36. Применение теоремы Фалеса для определения деталей фасада Решение: Отрезок В'В‘1 параллелен картине и не имеет точек
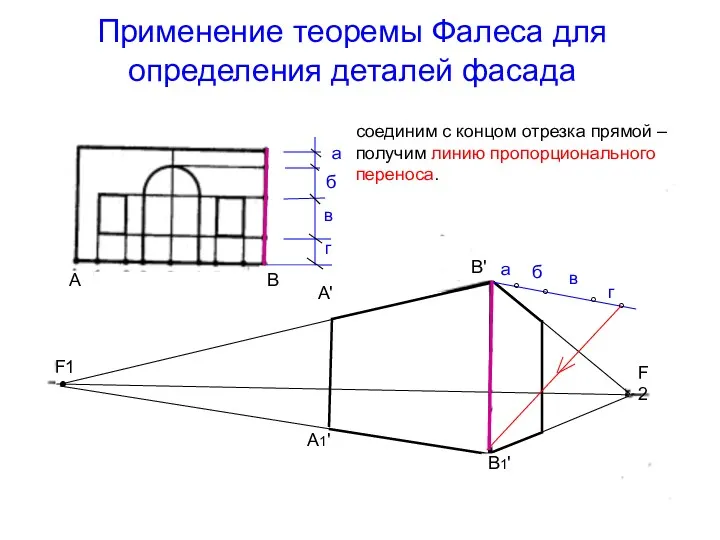
- 37. Применение теоремы Фалеса для определения деталей фасада соединим с концом отрезка прямой – получим линию пропорционального
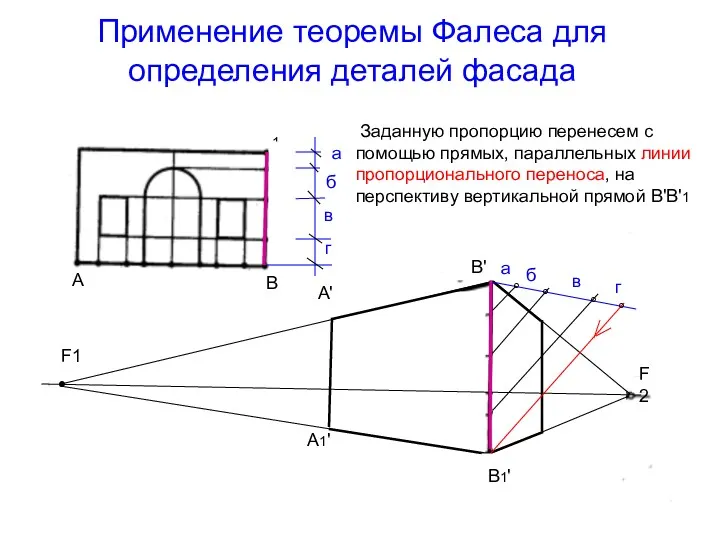
- 38. Применение теоремы Фалеса для определения деталей фасада Заданную пропорцию перенесем с помощью прямых, параллельных линии пропорционального
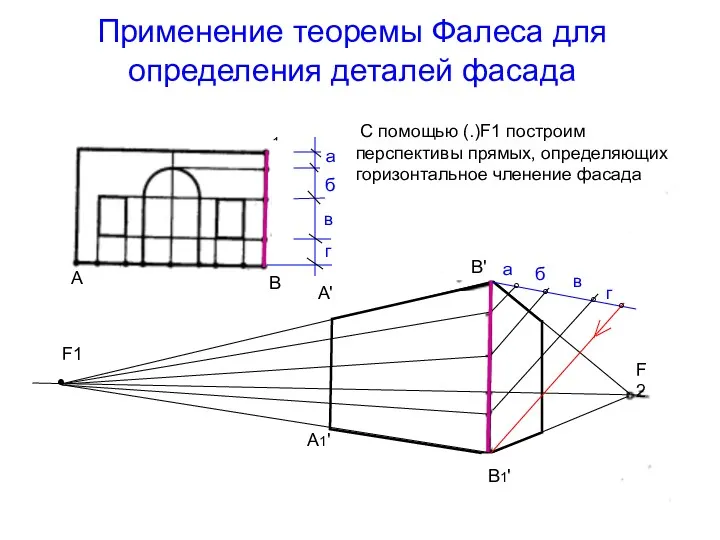
- 39. Применение теоремы Фалеса для определения деталей фасада С помощью (.)F1 построим перспективы прямых, определяющих горизонтальное членение
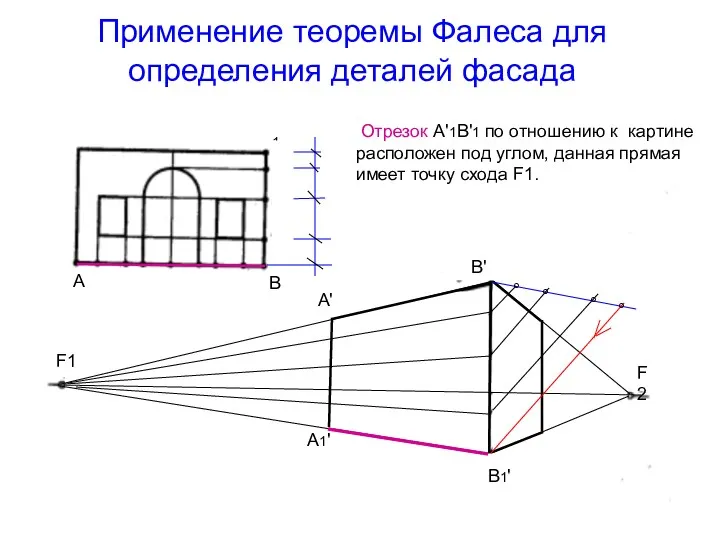
- 40. Применение теоремы Фалеса для определения деталей фасада Отрезок А'1В'1 по отношению к картине расположен под углом,
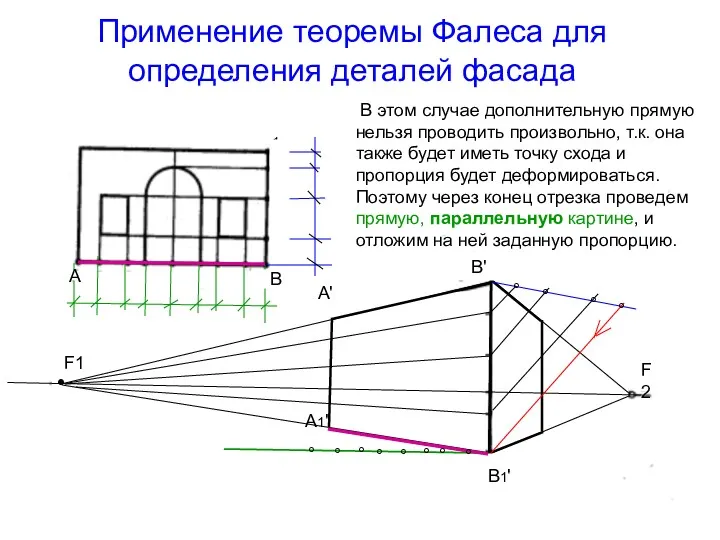
- 41. Применение теоремы Фалеса для определения деталей фасада В этом случае дополнительную прямую нельзя проводить произвольно, т.к.
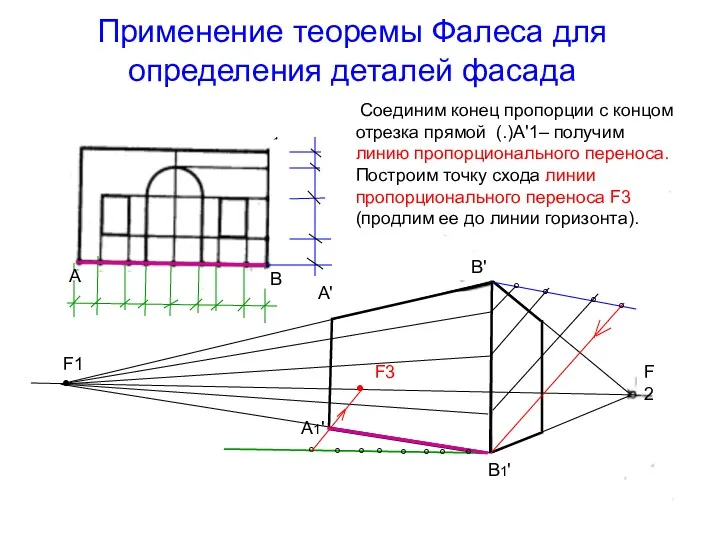
- 42. Применение теоремы Фалеса для определения деталей фасада Соединим конец пропорции с концом отрезка прямой (.)А'1– получим
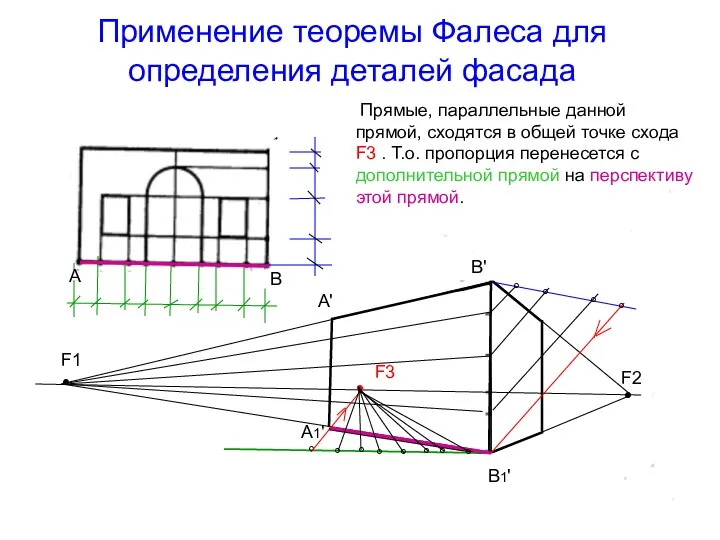
- 43. Применение теоремы Фалеса для определения деталей фасада Прямые, параллельные данной прямой, сходятся в общей точке схода
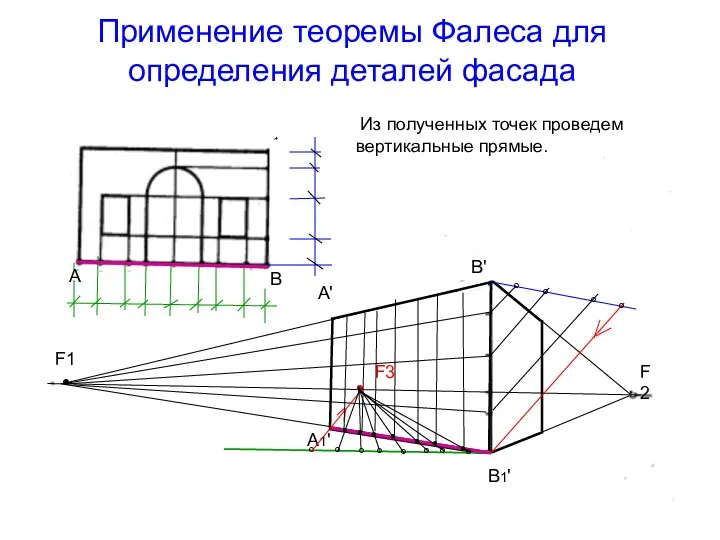
- 44. Применение теоремы Фалеса для определения деталей фасада Из полученных точек проведем вертикальные прямые. А1' А' В1'
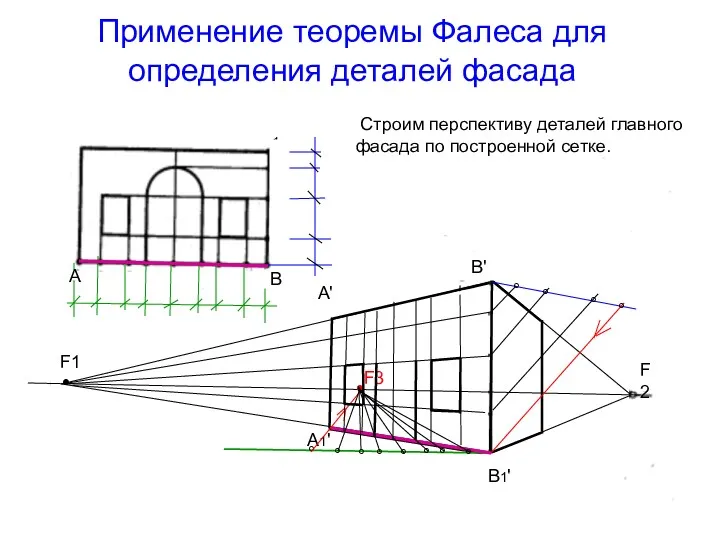
- 45. Применение теоремы Фалеса для определения деталей фасада Строим перспективу деталей главного фасада по построенной сетке. А1'
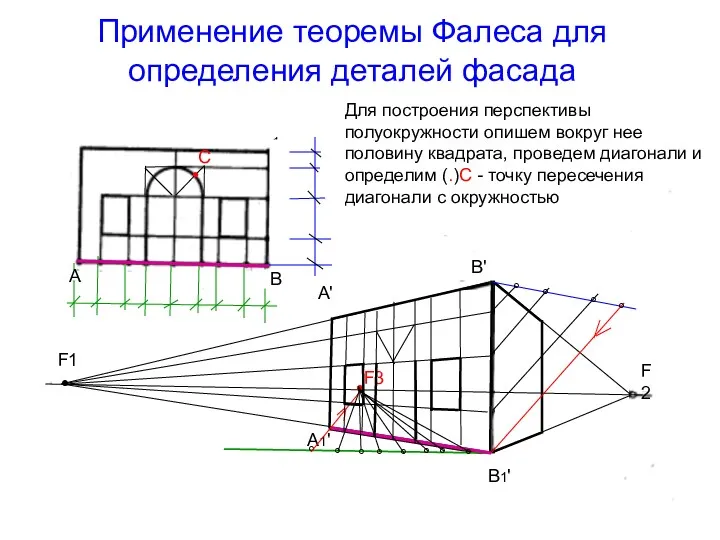
- 46. Применение теоремы Фалеса для определения деталей фасада Для построения перспективы полуокружности опишем вокруг нее половину квадрата,
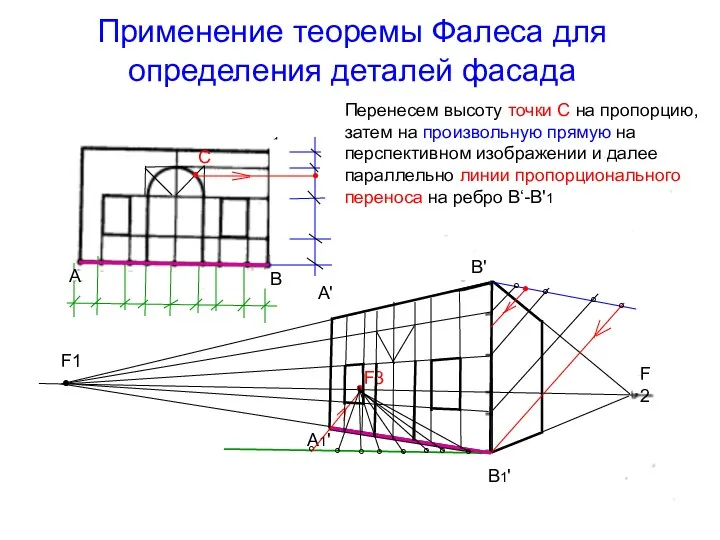
- 47. Применение теоремы Фалеса для определения деталей фасада Перенесем высоту точки С на пропорцию, затем на произвольную
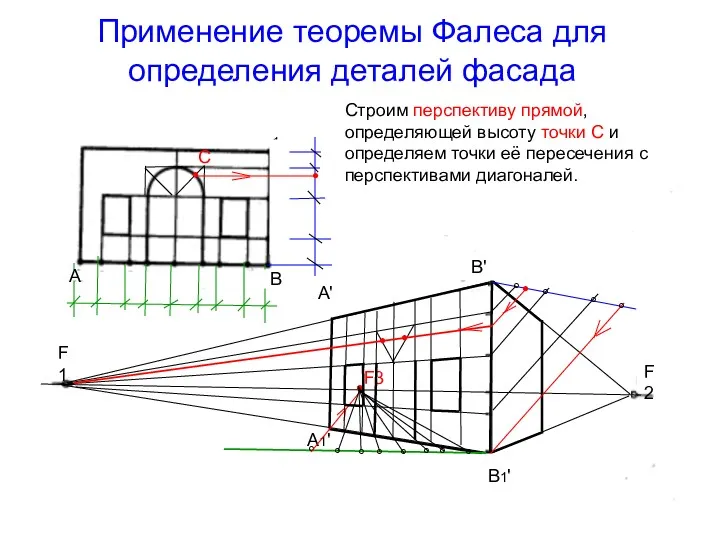
- 48. Применение теоремы Фалеса для определения деталей фасада Строим перспективу прямой, определяющей высоту точки С и определяем
- 50. Скачать презентацию







 Курсовое проектирование по дисциплине: Размерный анализ и обеспечение точности
Курсовое проектирование по дисциплине: Размерный анализ и обеспечение точности Өлшемдерді түсіру ережесі. Өлшем бірліктері
Өлшемдерді түсіру ережесі. Өлшем бірліктері Общие сведения о выполнении и оформлении сборочных чертежей. Лекция 8
Общие сведения о выполнении и оформлении сборочных чертежей. Лекция 8 Изображения – виды, разрезы, сечения
Изображения – виды, разрезы, сечения Кривые линии
Кривые линии Проектирование и монтаж станка-качалки для оборудования скважины с дебитом Q = 20 м3 /сутки и глубиной подвески насоса 1100 м
Проектирование и монтаж станка-качалки для оборудования скважины с дебитом Q = 20 м3 /сутки и глубиной подвески насоса 1100 м Плоскость. Положение плоскости в пространстве
Плоскость. Положение плоскости в пространстве Проецирование
Проецирование Правила оформления чертежа
Правила оформления чертежа Методы проецирования. Общие положения
Методы проецирования. Общие положения Местные разрезы. Особые случаи разрезов
Местные разрезы. Особые случаи разрезов Сборочный чертеж
Сборочный чертеж Резьба. Классификация резьбы. Изображение и обозначение резьбы на чертежах
Резьба. Классификация резьбы. Изображение и обозначение резьбы на чертежах Восходящие и нисходящие прямые. Разбивка окружностей в перспективе. Построение перспектив методом сетки
Восходящие и нисходящие прямые. Разбивка окружностей в перспективе. Построение перспектив методом сетки Аксонометрические проекции. Получение аксонометрической проекции
Аксонометрические проекции. Получение аксонометрической проекции Общие сведения об изделиях и конструкторских документах
Общие сведения об изделиях и конструкторских документах Сборочный чертёж
Сборочный чертёж Прямая и плоскость
Прямая и плоскость Состав проектной документации
Состав проектной документации Развёртки поверхностей. Аксонометрические проекции. Лекция 9
Развёртки поверхностей. Аксонометрические проекции. Лекция 9 Поєднання вигляду і розрізу
Поєднання вигляду і розрізу Деталирование сборочного чертежа. Порядок деталирования
Деталирование сборочного чертежа. Порядок деталирования Типы пневматических схем
Типы пневматических схем Прямая. Задание прямой
Прямая. Задание прямой Задание поверхностей на комплексном чертеже. Развертывающиеся линейчатые поверхности. Поверхности с плоскостью параллелизма
Задание поверхностей на комплексном чертеже. Развертывающиеся линейчатые поверхности. Поверхности с плоскостью параллелизма Несущий остов здания
Несущий остов здания Резьбовое содинение
Резьбовое содинение Перспектива та її особливості
Перспектива та її особливості