Поверхности. Способы задания поверхностей. Классификация поверхностей. Многогранники. Поверхности вращения второго порядка презентация
Содержание
- 2. ПОВЕРХНОСТЬ МНОЖЕСТВО ПОЛОЖЕНИЙ ЛИНИИ ПЕРЕМЕЩАЮЩЕЙСЯ В ПРОСТРАНСТВЕ ПО ОПРЕДЕЛЕННОМУ ЗАКОНУ
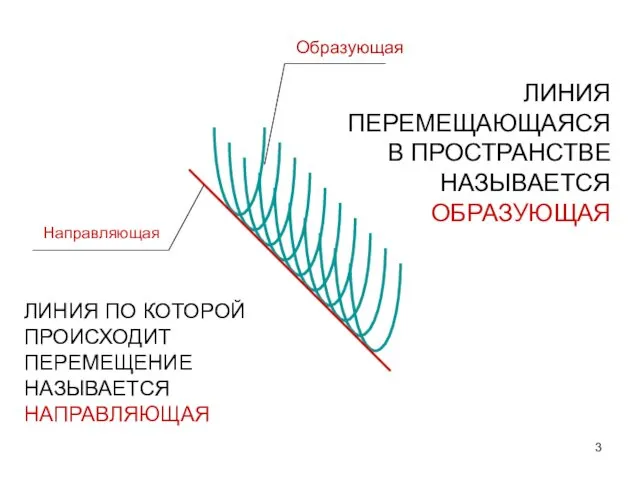
- 3. Направляющая Образующая ЛИНИЯ ПЕРЕМЕЩАЮЩАЯСЯ В ПРОСТРАНСТВЕ НАЗЫВАЕТСЯ ОБРАЗУЮЩАЯ ЛИНИЯ ПО КОТОРОЙ ПРОИСХОДИТ ПЕРЕМЕЩЕНИЕ НАЗЫВАЕТСЯ НАПРАВЛЯЮЩАЯ
- 4. СПОСОБЫ ЗАДАНИЯ ПОВЕРХНОСТЕЙ АНАЛИТИЧЕСКИЙ – X2 + Y2 + Z2 =1 2. ГРАФИЧЕСКИЙ: а) очерк б)
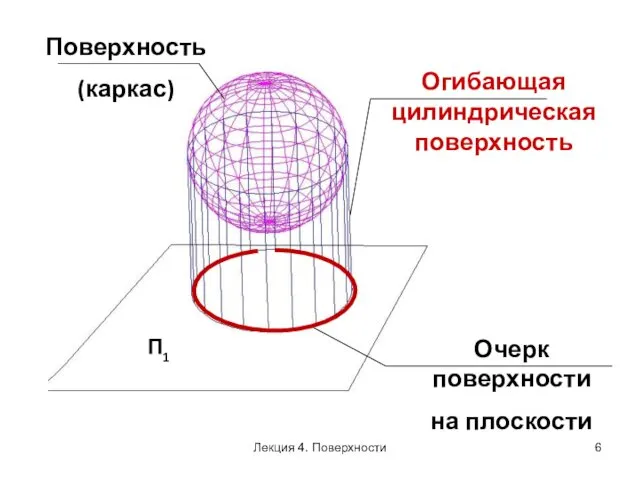
- 5. ОЧЕРК ПОВЕРХНОСТИ Следы проецирующей поверхности, огибающей заданную поверхность
- 6. П1 Очерк поверхности на плоскости Огибающая цилиндрическая поверхность Поверхность (каркас) Лекция 4. Поверхности
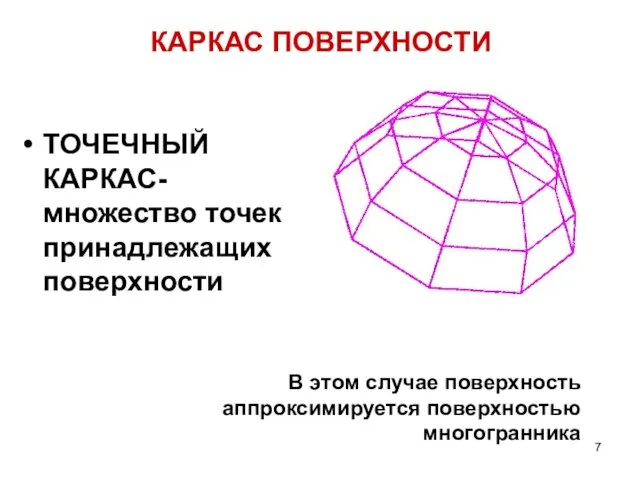
- 7. КАРКАС ПОВЕРХНОСТИ ТОЧЕЧНЫЙ КАРКАС- множество точек принадлежащих поверхности В этом случае поверхность аппроксимируется поверхностью многогранника
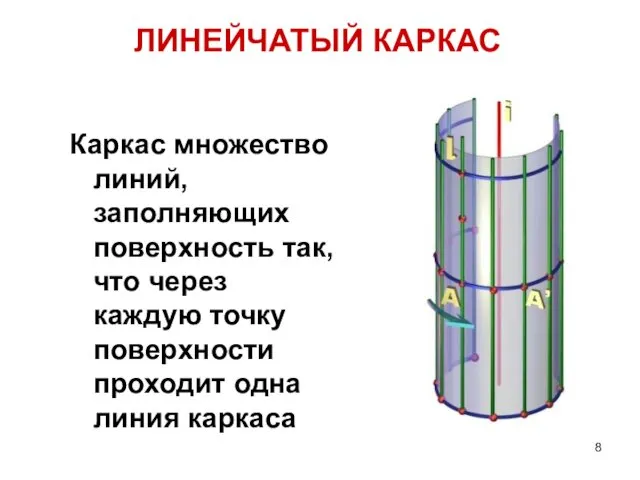
- 8. Каркас множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит одна линия каркаса ЛИНЕЙЧАТЫЙ
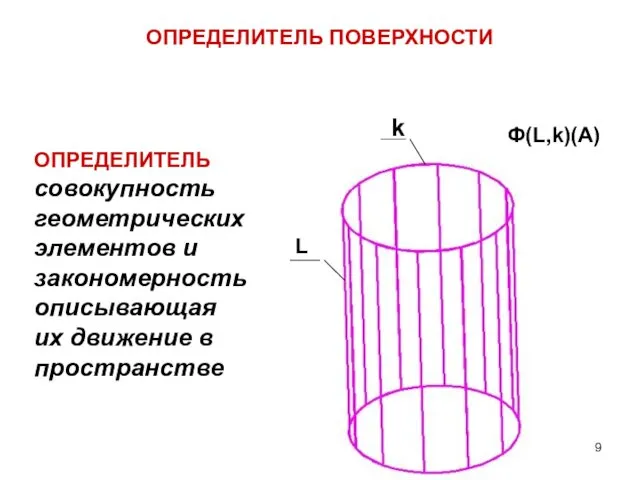
- 9. Ф(L,k)(A) ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ L k ОПРЕДЕЛИТЕЛЬ совокупность геометрических элементов и закономерность описывающая их движение в пространстве
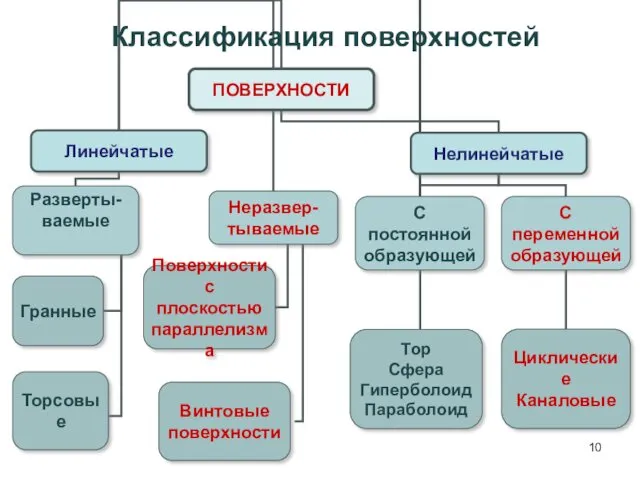
- 10. Классификация поверхностей
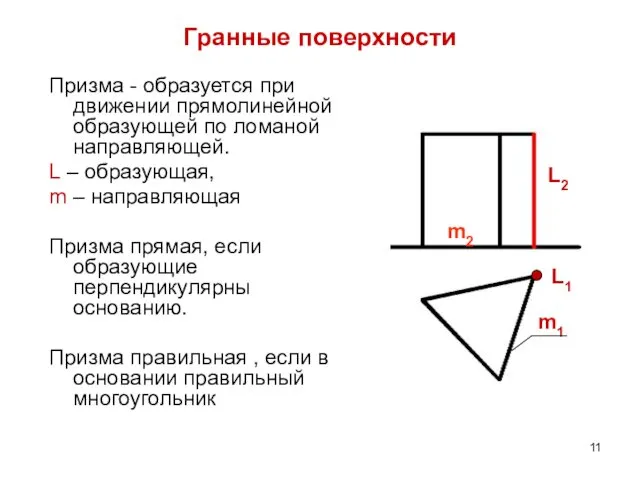
- 11. Гранные поверхности Призма - образуется при движении прямолинейной образующей по ломаной направляющей. L – образующая, m
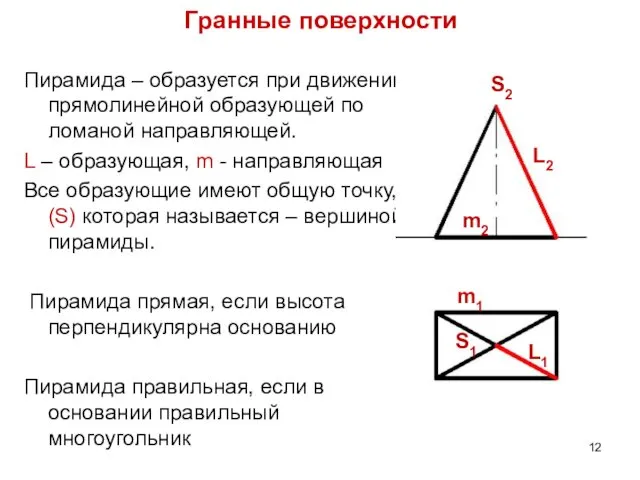
- 12. Гранные поверхности Пирамида – образуется при движении прямолинейной образующей по ломаной направляющей. L – образующая, m
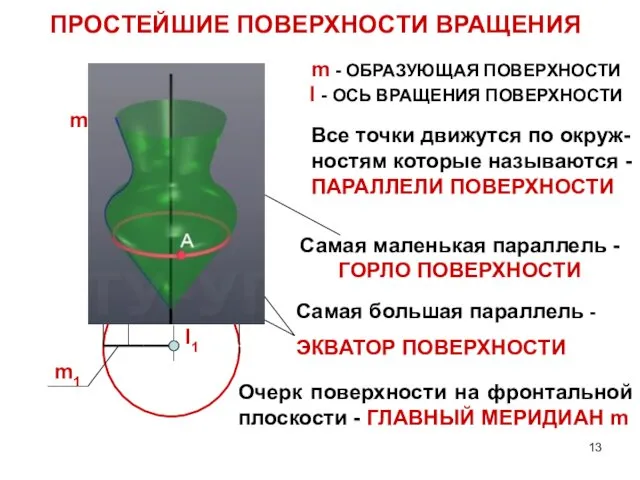
- 13. ПРОСТЕЙШИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ m - ОБРАЗУЮЩАЯ ПОВЕРХНОСТИ I - ОСЬ ВРАЩЕНИЯ ПОВЕРХНОСТИ Самая маленькая параллель -
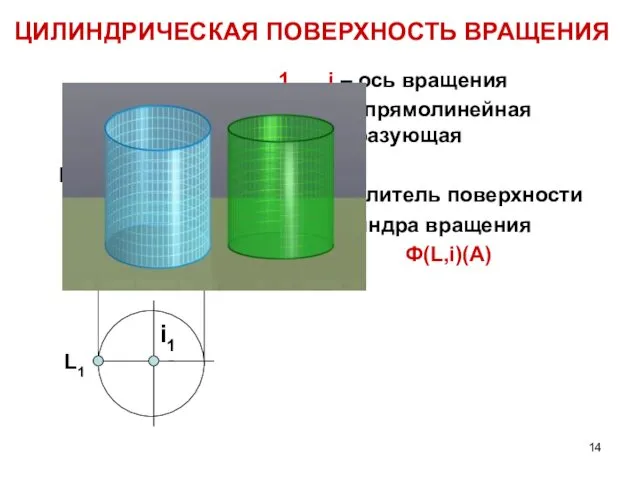
- 14. ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯ i – ось вращения 2. L – прямолинейная образующая Определитель поверхности цилиндра вращения
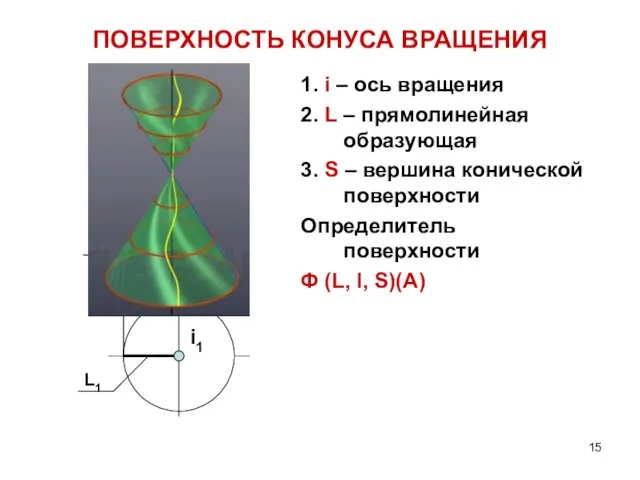
- 15. ПОВЕРХНОСТЬ КОНУСА ВРАЩЕНИЯ 1. i – ось вращения 2. L – прямолинейная образующая 3. S –
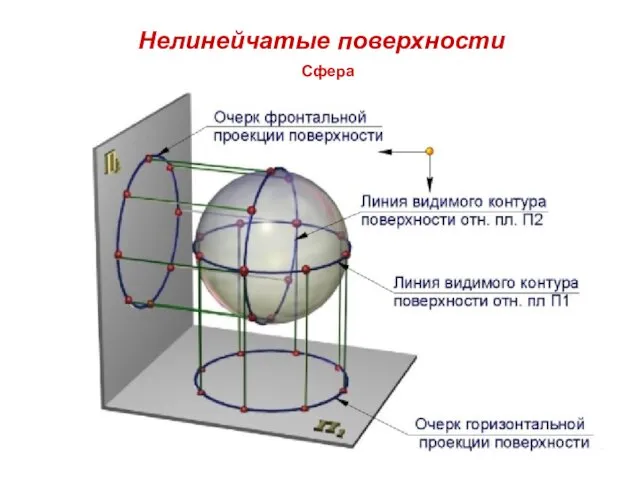
- 16. Нелинейчатые поверхности Сфера
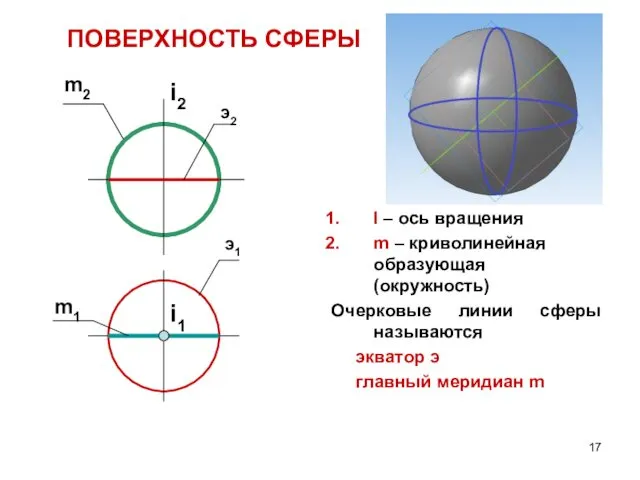
- 17. ПОВЕРХНОСТЬ CФЕРЫ I – ось вращения m – криволинейная образующая (окружность) Очерковые линии сферы называются экватор
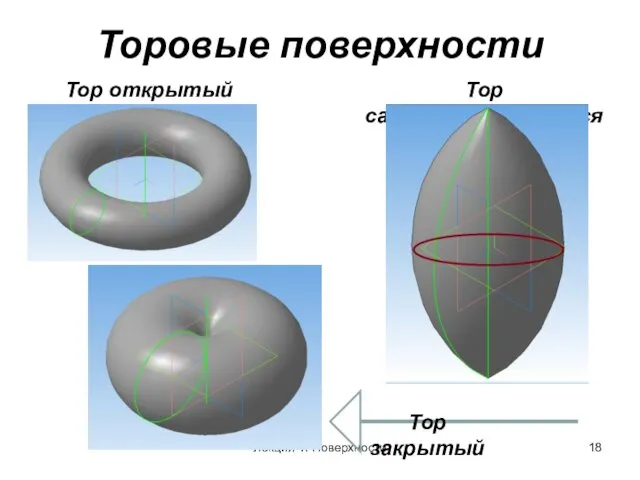
- 18. Торовые поверхности Тор открытый Лекция 4. Поверхности Тор самопересекающийся
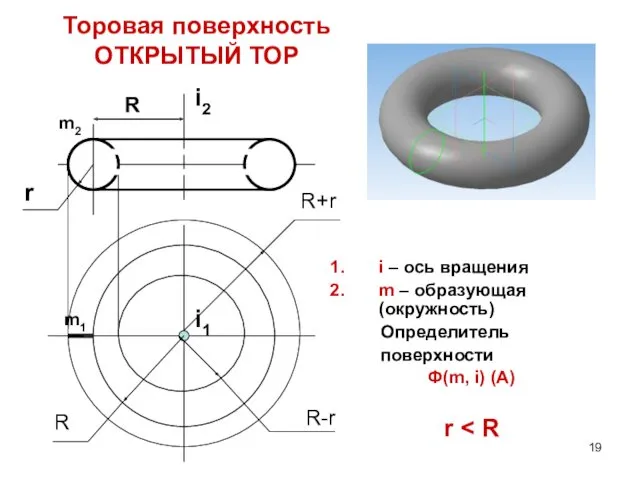
- 19. Торовая поверхность ОТКРЫТЫЙ ТОР i – ось вращения m – образующая (окружность) Определитель поверхности Ф(m, i)
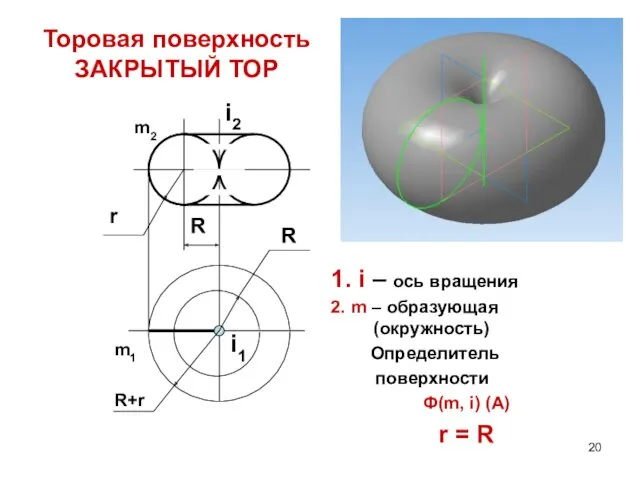
- 20. Торовая поверхность ЗАКРЫТЫЙ ТОР 1. i – ось вращения 2. m – образующая (окружность) Определитель поверхности
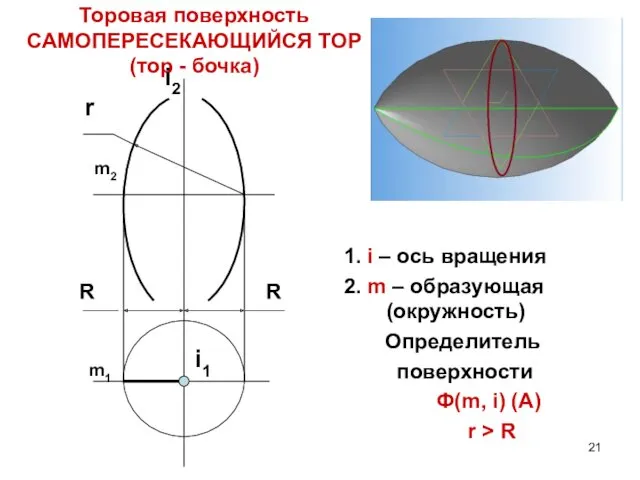
- 21. Торовая поверхность САМОПЕРЕСЕКАЮЩИЙСЯ ТОР (тор - бочка) 1. i – ось вращения 2. m – образующая
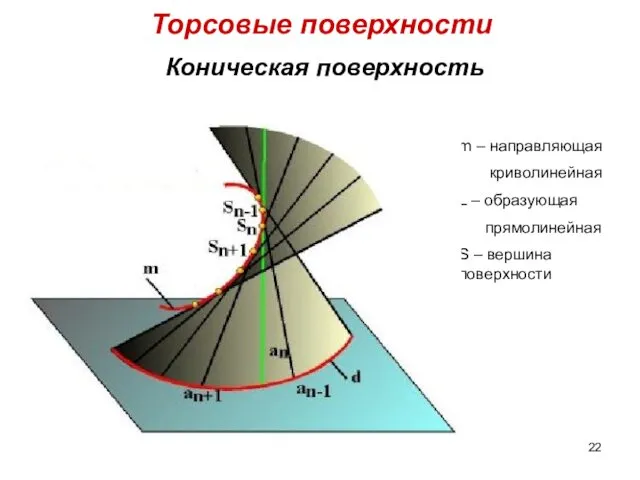
- 22. Коническая поверхность Торсовые поверхности X m2 m1 S2 S1 l2 l1 m – направляющая криволинейная L
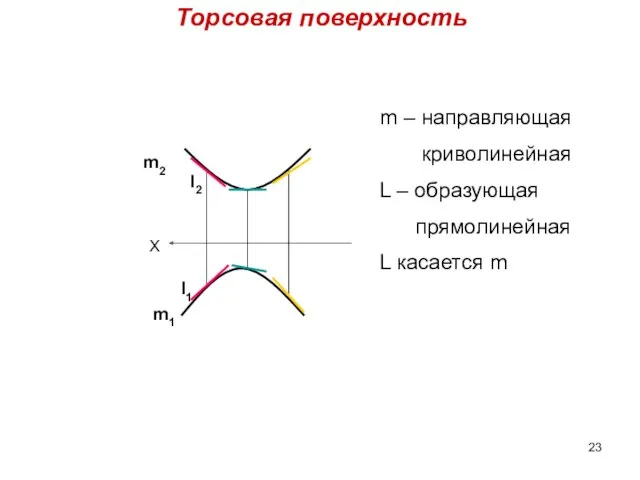
- 23. Торсовая поверхность X m2 m1 l2 l1 m – направляющая криволинейная L – образующая прямолинейная L
- 24. Поверхности Каталана (с плоскостью параллелизма) Цилиндроид Коноид Гиперболический параболоид (косая плоскость)
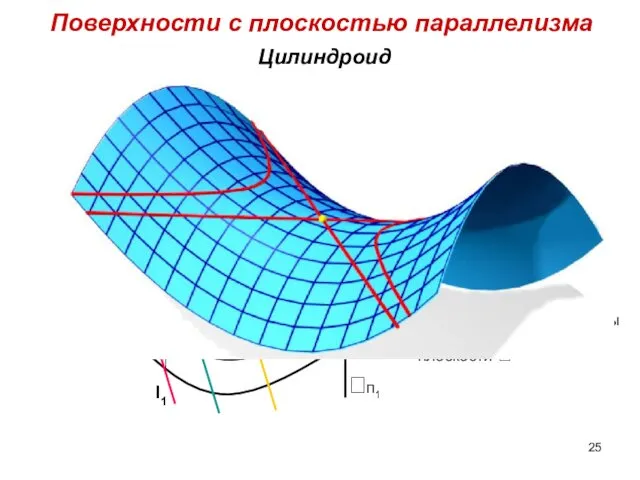
- 25. Поверхности c плоскостью параллелизма Цилиндроид X m2 n2 m1 n1 l2 l1 m – направляющая криволинейная
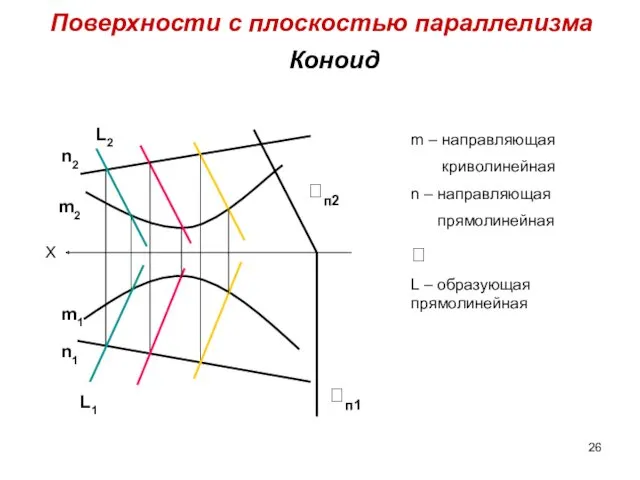
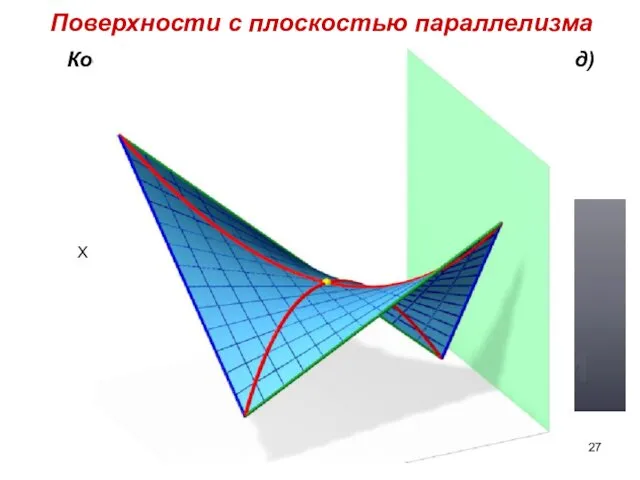
- 26. Коноид Поверхности c плоскостью параллелизма X m2 m1 n2 n1 L2 L1 m – направляющая криволинейная
- 27. Косая плоскость (гиперболический параболоид) Поверхности c плоскостью параллелизма X m2 m1 n2 n1 L2 L1
- 28. ВИНТОВЫЕ ПОВЕРХНОСТИ Прямой и наклонный геликоид – частный случай поверхности коноида (прямолинейная образующая, две направляющие –
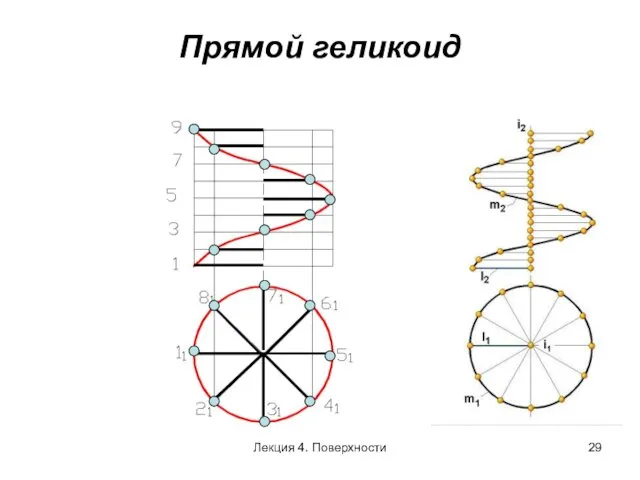
- 29. Прямой геликоид Лекция 4. Поверхности
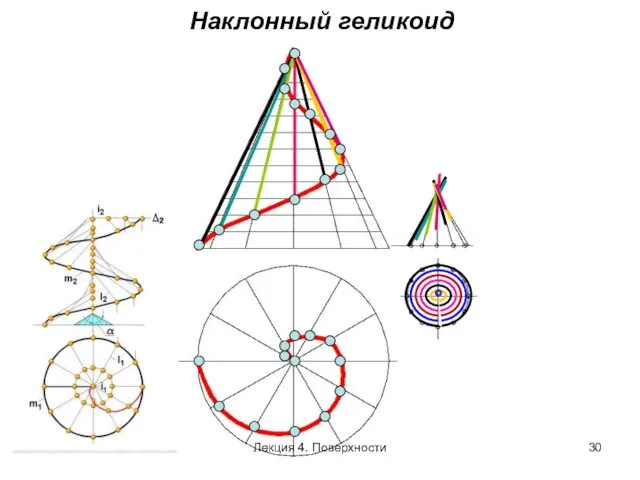
- 30. Наклонный геликоид Лекция 4. Поверхности
- 31. Выводы по теме Поверхностью называется множество положений линий, перемещающейся в пространстве по определенному закону Поверхности подразделяются
- 32. Рекомендованная литература Бударин О. С. Начертательная геометрия. Краткий курс: учеб. пособие для студентов вузов, обучающихся по
- 34. Скачать презентацию







 Построение плана этажа
Построение плана этажа Геометрические основы теории теней. (Лекция 4-6)
Геометрические основы теории теней. (Лекция 4-6) Типы пневматических схем
Типы пневматических схем Поверхности. Лекция 7
Поверхности. Лекция 7 Введение. Методы проецирования. Точка. Проецирование точки
Введение. Методы проецирования. Точка. Проецирование точки Группа жилых домов средней этажности в Сокольниках
Группа жилых домов средней этажности в Сокольниках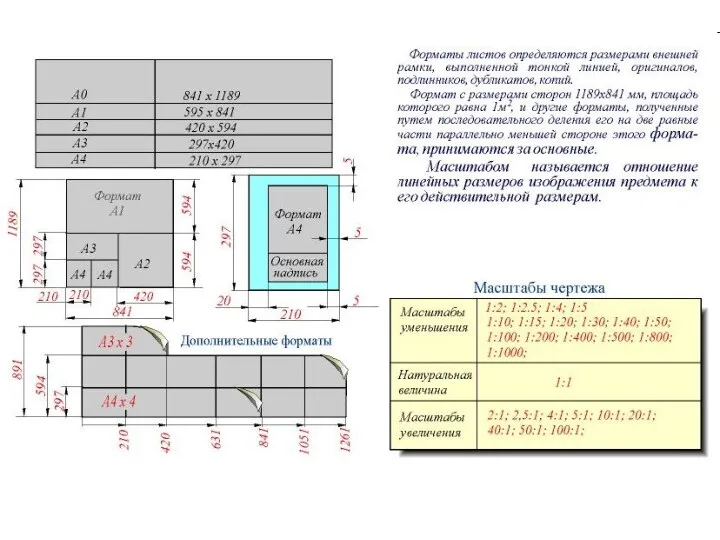 Проекционное черчение
Проекционное черчение Виды. Основные виды
Виды. Основные виды Проецирование. ИЗО 8 класс
Проецирование. ИЗО 8 класс Чертежный шрифт
Чертежный шрифт Проецирование
Проецирование Построения чертежей контуров технических деталей с использованием методов деления окружности на равные части
Построения чертежей контуров технических деталей с использованием методов деления окружности на равные части Конструкторско-технологическая подготовка производства модернизации привода главного движения станка модели 1к62
Конструкторско-технологическая подготовка производства модернизации привода главного движения станка модели 1к62 Пересечение поверхностей вращения плоскостями
Пересечение поверхностей вращения плоскостями Методы проецирования. Общие положения
Методы проецирования. Общие положения Сборочный чертеж и деталирование сборочной единицы
Сборочный чертеж и деталирование сборочной единицы Технический рисунок. 8 класс
Технический рисунок. 8 класс Общие правила оформление чертежей. Линии чертежа
Общие правила оформление чертежей. Линии чертежа Выполненный вариант контрольной работы по разделу Техническое черчение. (Приложение 3)
Выполненный вариант контрольной работы по разделу Техническое черчение. (Приложение 3) Оформление чертежей. Стандарты ЕСКД
Оформление чертежей. Стандарты ЕСКД Виды изделий. Конструктивные элементы деталей (лекция № 3)
Виды изделий. Конструктивные элементы деталей (лекция № 3) Начертательная геометрия
Начертательная геометрия Виадук Мийо
Виадук Мийо Сборочные чертежи. Разъёмные и неразъёмные соединения деталей
Сборочные чертежи. Разъёмные и неразъёмные соединения деталей II международная научно-практическая конференция. BIM-моделирование в задачах строительства и архитектуры
II международная научно-практическая конференция. BIM-моделирование в задачах строительства и архитектуры Изображения – виды, разрезы, сечения
Изображения – виды, разрезы, сечения Начертательная геометрия. Точка, линии
Начертательная геометрия. Точка, линии Поверхности. Задание поверхности на чертеже
Поверхности. Задание поверхности на чертеже