Содержание
- 2. Эконометрика и эконометрическое моделирование: основные понятия и определения
- 3. Под экономическим объектом будем понимать любой элемент экономики (микроуровень: фирмы, семьи, предприятия; мезоуровень: регионы, отдельный сектор
- 4. Эконометрика — это научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенная для того,
- 5. Эконометрика является одним из разделов математического моделирования экономических процессов, который базируется: • на экономической теории; •
- 6. Этапы построения эконометрических моделей и принципы спецификации
- 7. Построение эконометрических моделей (как и экономико-математических) выполняется в несколько этапов: 1) спецификация модели; 2) сбор статистической
- 8. Экономико-математическая модель объекта (математическая модель экономического объекта) представляет собой математически выраженную связь между его экономическими переменными.
- 9. По отношению к выбранной спецификации все экономические переменные объекта подразделяются на два типа: эндогенные экзогенные.
- 10. Определение Экзогенными (независимыми) называются экономические переменные, значения которых определяются вне данной модели.
- 11. Эндогенными (зависимыми) называются экономические переменные, значения которых определяются (объясняются) внутри модели в результате одновременного взаимодействия соотношений,
- 12. Определение При наличии хотя бы одной экзогенной переменной модель называется открытой, в противном случае — замкнутой.
- 13. Первый принцип спецификации Экономико-математическая модель строится по результатам математической формализации закономерностей общей экономической теории.
- 14. Второй принцип спецификации В правильно составленной спецификации содержится столько уравнений, сколько эндогенных переменных включается в модель
- 15. Третий принцип спецификации Учет фактора времени в экономических моделях, или датирование экономических переменных.
- 16. Определение Переменные модели называются датированными, если обозначена их зависимость от времени.
- 17. Если экономические утверждения отражают статическую (относящуюся к одному периоду времени) взаимосвязь всех включённых в модель переменных,
- 18. Если экономические утверждения отражают динамическую (зависящую от фактора времени) взаимосвязь включённых в модель переменных, то значения
- 19. Определение Лаговыми называются экзогенные или эндогенные переменные экономической модели, датированные предыдущими моментами времени и находящиеся в
- 20. Модели, включающие лаговые переменные, относятся к классу динамических моделей.
- 21. Определение Предопределёнными называются лаговые и текущие экзогенные переменные, а также лаговые эндогенные переменные.
- 22. Четвертый принцип спецификации Включение случайных возмущений в спецификацию экономической модели.
- 23. Экономические модели со случайными возмущениями принято называть эконометрическими.
- 24. На первом этапе построения эконометрических моделей, то есть — спецификации модели привлекается общая экономическая теория и
- 25. Поэтому для построения оценок (или прогнозов) значений эндогенных переменных необходимо привлечь результаты статистических наблюдений за данным
- 26. Далее, на основании статистической информации при помощи статистических методов (как правило, методов регрессионного анализа) выполняется оценка
- 27. Таким образом, на втором и третьем этапах привлекается третья составляющая эконометрики — статистика (теория статистических измерений
- 28. Следующий этап построения эконометрической модели — верификация (проверка адекватности модели). На данном этапе проверяется соответствие модели
- 29. Структурная и приведенная формы эконометрических моделей Для построения прогнозов эндогенных переменных необходимо выразить текущие эндогенные переменные
- 30. В модели равновесного рынка только переменная предложения выражена в явном виде через предопределенную переменную, поэтому для
- 31. Получим Ytd =a0+a1 pt+a2 xt+ut, a1 0, Ys =b0+b1 pt-1+vt, b1>0 Ytd =Yts
- 32. Подставим первое и второе уравнения в третье, а0 + а1 pt +а2 хt +ut =b0 +b1
- 33. Окончательно получим выражение спроса через предопределенные переменные: Таким образом, после преобразований спецификация модели принимает следующий вид:
- 34. Таким образом, эндогенные переменные модели выражены в явном виде через предопределенные переменные. Такая форма спецификации получила
- 35. Матричная запись структурной и приведенной форм моделей Введем следующие обозначения: Yt — вектор-столбец текущих значений эндогенных
- 36. Представим спецификацию модели равновесного рынка в матричной форме. Для этого предварительно в каждом уравнении системы перенесем
- 37. Предопределенные переменные модели: лаговое значение цены товара; текущий доход потребителя. Расширенный вектор X, включает три элемента:
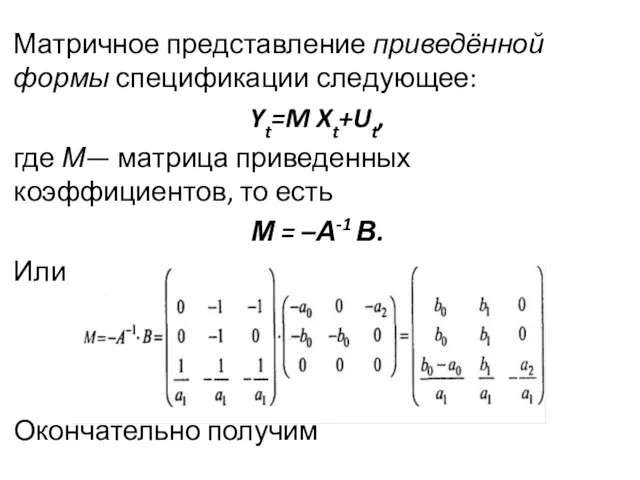
- 38. Матричное представление приведённой формы спецификации следующее: Yt=M Xt+Ut, где М— матрица приведенных коэффициентов, то есть М
- 39. Окончательно получим Вектор случайных возмущений в приведённой форме получается в результате преобразования Ut = A-1 Vt
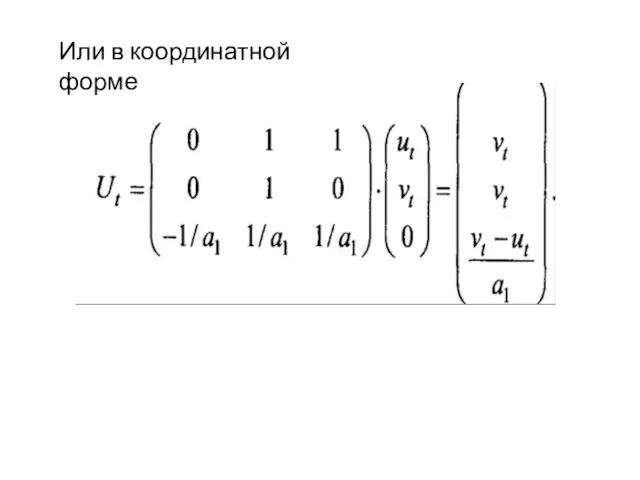
- 40. Или в координатной форме
- 41. Пример. Модель формирования национального дохода (Дж. М. Кейнс)
- 42. Исследуемым экономическим объектом является закрытая национальная экономика без государственного вмешательства. Экономические переменные модели: Y, С, I,
- 43. Требуется: A. Составить спецификацию макромодели, позволяющей объяснять величины Y (национального дохода) и С (объем потребления) уровнем
- 44. При составлении спецификации модели воспользоваться следующими утверждениями экономической теории: 1) потребление возрастает с увеличением совокупного выпуска,
- 45. Б. Уточнить спецификацию путем датирования переменных. При датировании экономических переменных данной модели следует учесть еще один
- 46. B. Уточнить спецификацию включением случайного возмущения. Г. Составить приведенную форму спецификации. Д. Записать структурную и приведенную
- 47. Решение. Воспользуемся первым принципом спецификации и формализуем экономические законы, характеризующие данный экономический объект.
- 48. А. Исходя из первой закономерности экономической теории, имеем: C = a+bY, 0 0, где а —
- 49. Из второй предпосылки следует тождество Y = C + I. Таким образом, структурная форма модели, полученная
- 50. Вывод Спецификация составлена правильно, так как в структурной форме, в соответствии со вторым принципом, должно быть
- 51. Б. Третий принцип спецификации — датирование переменных. Необходимо уточнить спецификацию: датировать экономические переменные, т. е. учесть
- 52. При датировании экономических переменных данной модели следует учесть тот факт, что текущее потребление зависит от совокупного
- 53. В. Уточним спецификацию включением случайного возмущения, г. с. перейдем от экономической модели к эконометрической. Случайные возмущения
- 54. В спецификации поведенческим уравнением является первое, таким образом, спецификация эконометрической модели, составленная с использованием четырех принципов,
- 55. Г. Составим приведенную форму спецификации. Решим систему и выразим эндогенные переменные модели через предопределенные и явном
- 56. Д. Матричный вид структурной и приведенной форм спецификации. Сформируем векторы эндогенных и предопределенных переменных модели. Вектор-столбец
- 57. Запишем уравнения структурной формы в следующем виде: Сt – a bYt-1 = εt , Yt –
- 58. Решим матричное уравнение относительно вектора эндогенных переменных Yt=–A-1B Xt +A-1 Vt = M Xt + Ut,
- 59. Приведенная форма модели принимает вид
- 60. Парная линейная регрессия Сущность регрессионного анализа
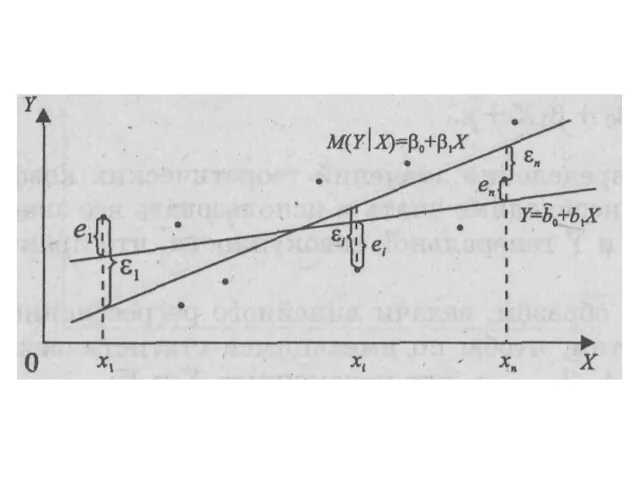
- 61. Функция регрессии Y на X. M(Y│x) = f(x), Где X - независимая (объясняющая) переменная (регрессор), Y
- 62. Регрессионные модели (уравнения) Y = M(Y│x) + ε, Y = M(Y│x1, x2, ...,xm) + ε,
- 63. Причины обязательного присутствия в регрессионных моделях случайного фактора (отклонения) 1. Невключение в модель всех объясняющих переменных.
- 64. Этапы построения уравнения регрессии 1) выбор формулы уравнения регрессии; 2) определение параметров выбранного уравнения; 3) анализ
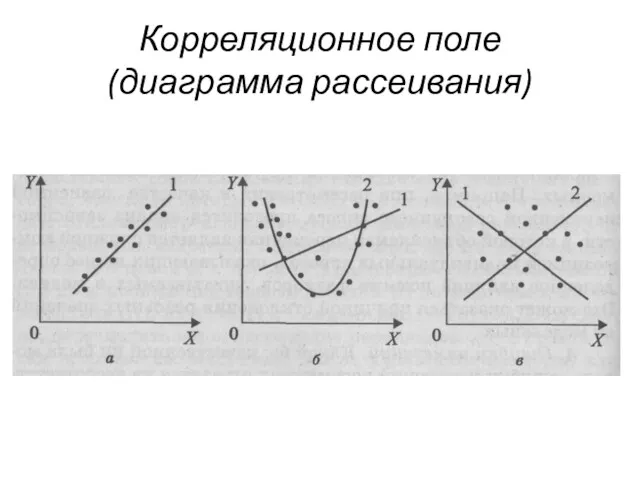
- 65. Корреляционное поле (диаграмма рассеивания)
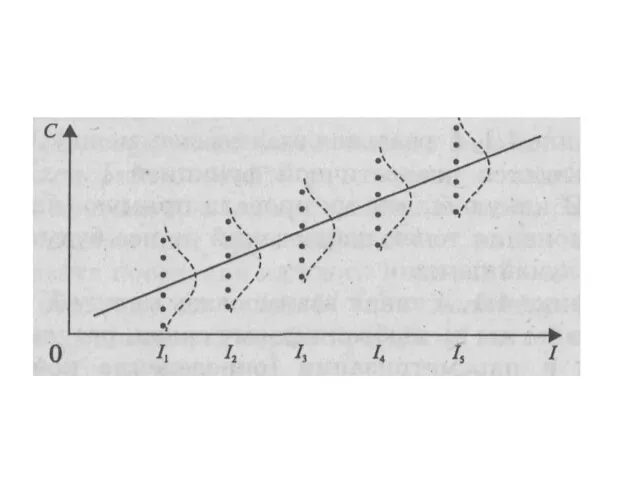
- 66. Парная линейная регрессия Модель Кейнса I = С = С0 + bI, где С0 —величина автономного
- 68. линейная регрессия (теоретическое линейное уравнение регрессии) М(Y|х = xi)=β0 + β1 xi, Или со случайным параметром
- 69. Задачи линейного регрессионного анализа 1. По имеющимся статистическим данным (xi, yi), i = 1, 2, ...,
- 70. Эмпирическое уравнение регрессии =b0 + b1 x1, где — оценка условного математического ожидания M(Y │X =
- 72. Оценка тесноты связи Мерой линейной зависимости двух случайных величин является ковариация этих величин, определяемая выражением
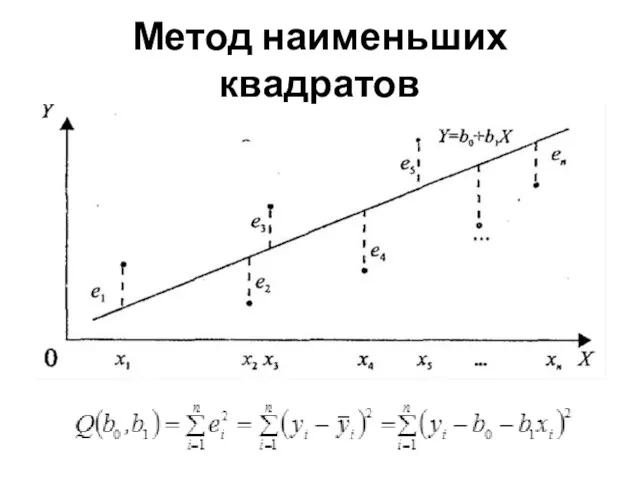
- 73. Нахождение коэффициентов b0 и b1 эмпирического уравнения регрессии
- 74. Возможные методы нахождения коэффициентов b0 и b1 эмпирического уравнения регрессии метод наименьших модулей (МНМ). метод наименьших
- 75. Метод наименьших квадратов
- 78. Если, кроме уравнения регрессии Y на X (Y = b0 + b1Х), для тех же эмпирических
- 79. Выводы 1. Оценки МНК являются функциями от выборки, что позволяет их легко рассчитывать. 2. Оценки МНК
- 80. 5.П Случайные отклонения ei не коррелированы с наблюдаемыми значениями yi зависимой переменной Y. 6. Случайные отклонения
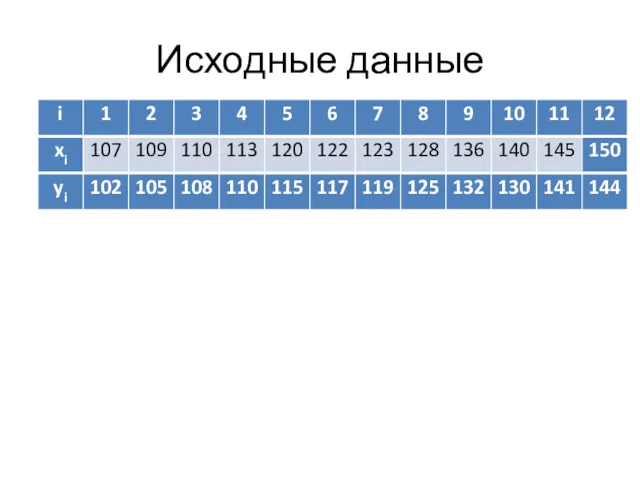
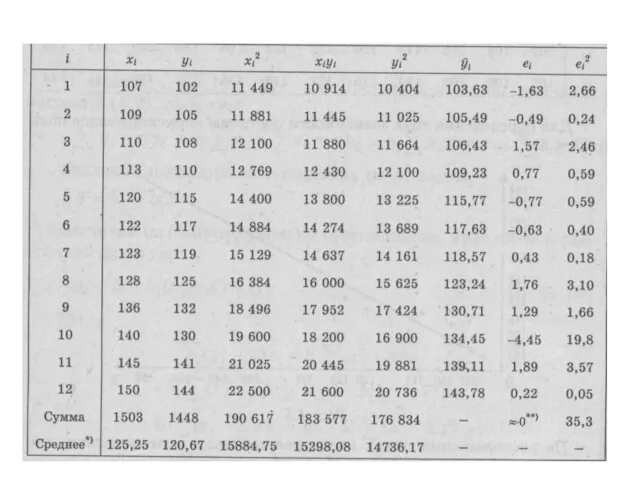
- 81. Пример Для анализа зависимости объема потребления Y(у.е.) домохозяйства от располагаемого дохода X(у.е.) отобрана выборка объема п
- 82. Исходные данные
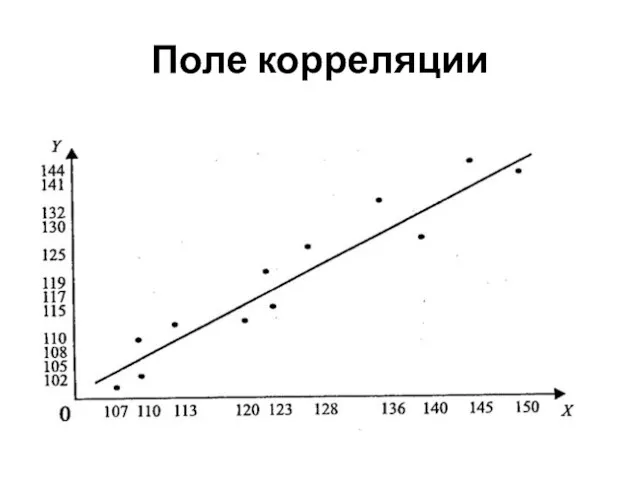
- 83. Поле корреляции
- 86. Выводы Прогнозируемое потребление при располагаемом доходе х = 160 по данной модели составит y(160) ≈ 153,12.
- 87. На графике коэффициент b1 определяет тангенс угла наклона прямой регрессии относительно положительного направления оси абсцисс (объясняющей
- 88. Очень важно, насколько далеко данные наблюдений за объясняющей переменной отстоят от оси ординат (зависимой переменной), так
- 89. Этот факт можно объяснить для отдельного домохозяйства (оно может тратить накопленные или одолженные средства), но для
- 90. Следует помнить, что эмпирические коэффициенты регрессии b0 и b1 являются лишь оценками теоретических коэффициентов β0 и
- 91. Однако при определенных условиях уравнение регрессии служит незаменимым и очень качественным инструментом анализа и прогнозирования. Обсуждение
- 92. ПРОВЕРКА КАЧЕСТВА УРАВНЕНИЯ РЕГРЕССИИ Классическая линейная регрессионная модель
- 93. Рассмотрим модель парной линейной регрессии Y = β0 + β 1X + ε.
- 94. Предпосылки метода наименьших квадратов 1 . Математическое ожидание случайного отклонения εi равно нулю: M(εi) = 0
- 95. 2. Дисперсия случайных отклонений, постоянна: D(εi) = D(εj) =σ2 для любых наблюдений i и j. Данное
- 96. 3. Случайные отклонения εi и εj являются независимыми друг от друга для i ≠ j. Выполнимость
- 98. 4. Случайное отклонение должно быть независимо от объясняющих переменных. Обычно это условие выполняется автоматически, если объясняющие
- 99. Теорема Гаусса-Маркова Если предпосылки 1 — 5 выполнены, то оценки, полученные по МНК, обладают следующими свойствами:
- 100. 2. Оценки состоятельны, так как дисперсия оценок параметров при возрастании числа п наблюдений стремится к нулю.
- 101. Анализ точности определения оценок коэффициентов регрессии Модель парной линейной регрессии Y = β0 + β 1X
- 102. где То есть коэффициент b1 также является случайным, так как значение выборочной ковариации Sxy зависит от
- 103. Теоретически коэффициент b1 можно разложить на неслучайную и случайную составляющие. Sxy = cov (X, β0 +
- 104. Следовательно, Здесь β1 — постоянная величина (истинное значение коэффициента регрессии); — случайная компонента. Аналогичный результат можно
- 105. Вывод На практике такое разложение осуществить невозможно, поскольку неизвестны истинные значения β0 и β1, а также
- 106. Найдем формулы связи дисперсий коэффициентов D(b0) и D(b1) с дисперсией σ2 случайных отклонений εi. Для этого
- 107. имеем: где
- 109. выводы • Дисперсий b0 и b1 прямо пропорциональны дисперсии случайного отклонения σ2. Следовательно, чем больше фактор
- 110. Чем больше дисперсия (разброс значений ) объясняющей переменной, тем меньше дисперсия оценок коэффициентов. Другими словами, чем
- 111. В силу того что случайные отклонения εi по выборке определены быть не могут, при анализе надежности
- 112. Диcперсия случайных отклонений D(εi) = σ2 заменяется ее несмещенной оценкой Тогда
- 113. Где - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии). Корень квадратный из необъясненной дисперсии
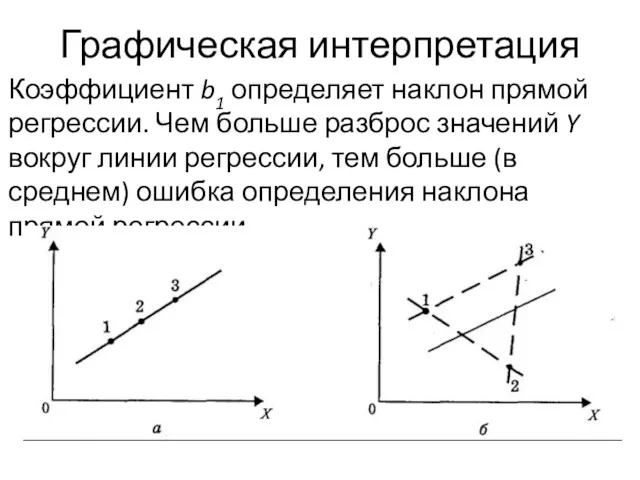
- 114. Графическая интерпретация Коэффициент b1 определяет наклон прямой регрессии. Чем больше разброс значений Y вокруг линии регрессии,
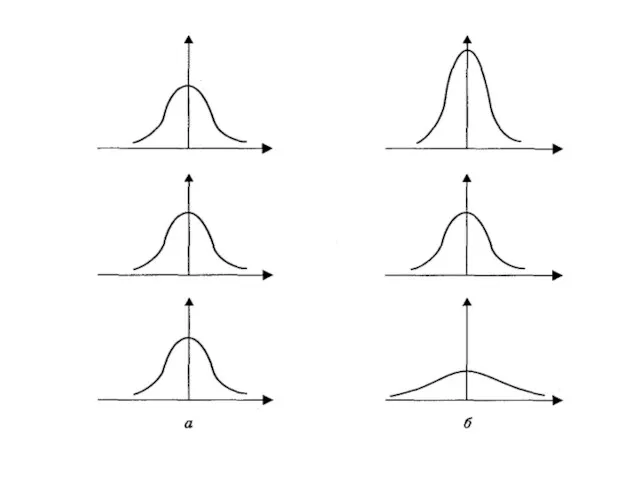
- 115. Например, на рис. а все наблюдаемые точки лежат на одной прямой. Тогда через любой набор точек
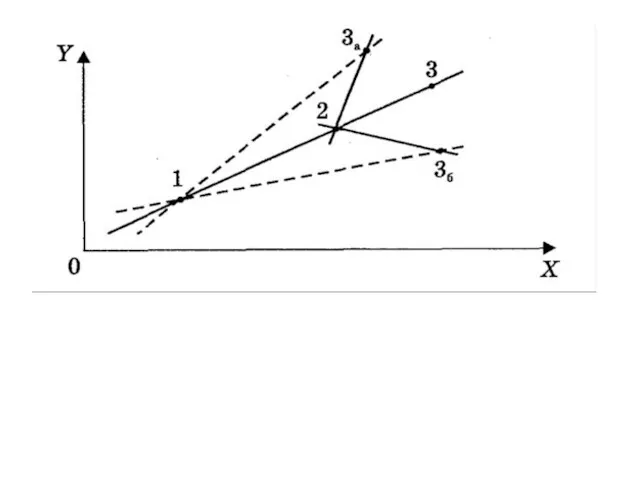
- 116. В выражении, определяющим значение стандартной ошибки коэффициента регрессии b1, стоит сумма квадратов отклонений xi от среднего
- 117. Например, на рис. через пары точек (1, 3) и (2, 3) проведена одна и та же
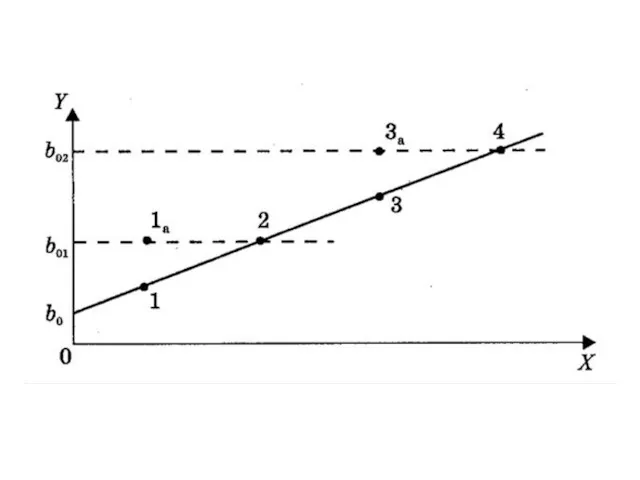
- 119. Дисперсия свободного члена уравнения регрессии пропорциональна дисперсии коэффициента регрессии. Действительно, чем сильнее меняется наклон прямой, проведенной
- 121. На рис. через пары точек (1, 2) и (3, 4) проходит одна и та же прямая,
- 122. Проверка гипотез относительно коэффициентов линейного уравнения регрессии Эмпирическое уравнение регрессии определяется на основе конечного числа статистических
- 123. При проведении статистического анализа перед исследователем зачастую возникает необходимость сравнения эмпирических коэффициентов регрессии b0 и b1
- 124. Статистической называют гипотезу о виде закона распределения или о параметрах известного распределения. В первом случае гипотеза
- 125. Например, если проверяется гипотеза о равенстве параметра θ некоторому значению θ0, т.е. Н0: θ = θ0,
- 126. Гипотезу называют простой, если она содержит одно конкретное предположение Гипотезу называют сложной, если она состоит из
- 127. При проверке гипотезы выборочные данные могут противоречить гипотезе Н0. Тогда она отклоняется. Если же статистические данные
- 128. При этом возможны ошибки двух родов: Ошибка первого рода состоит в том, что будет отвергнута правильная
- 129. результаты статистических выводов
- 130. Вероятность совершить ошибку первого рода принято обозначать буквой α, и ее называют уровнем значимости. Вероятность совершить
- 131. Наиболее известные случайные величины (статистики, критерии) U (или Z) — стандартизированное нормальное распределение; Т — если
- 132. В целях общности будем обозначать такую случайную величину через К. Основной принцип проверки статистических гипотез можно
- 133. Вероятность того, что случайная величина К попадет в произвольный интервал ( ), можно найти по формуле
- 134. Следовательно
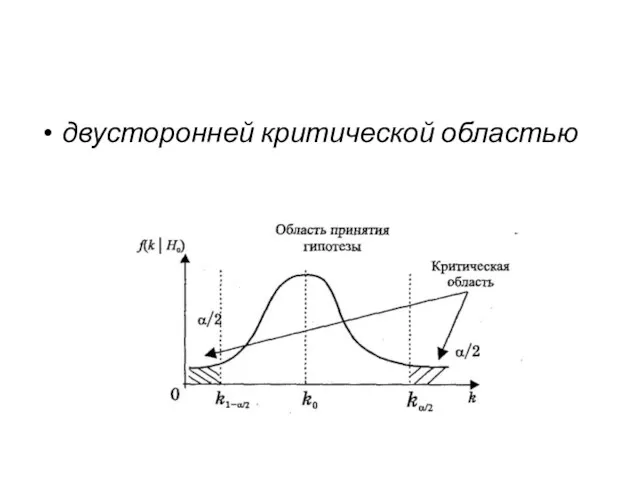
- 135. двусторонней критической областью
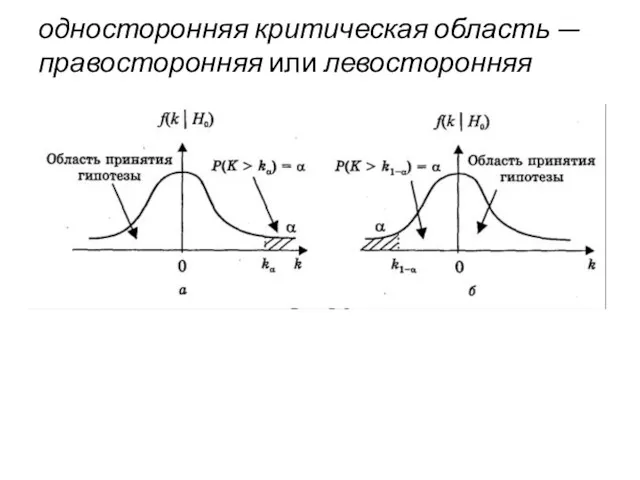
- 136. односторонняя критическая область — правосторонняя или левосторонняя
- 137. Общая схема проверки гипотез 1. Формулировка проверяемой (нулевой — Н0) и альтернативной (H1) гипотез. 2. Выбор
- 138. Проверка гипотез и доверительные интервалы Для проверки гипотезы H0 : b1 = β1, H1 : b1
- 139. Следовательно, H0 : b1 = β1 отклоняется на основании данного критерия, если где α — требуемый
- 140. Наиболее важной на начальном этапе статистического анализа построенной модели все же является задача установления наличия линейной
- 141. В этом случае говорят, что коэффициент b1 статистически незначим (он слишком близок к нулю). При отклонении
- 142. Поскольку полагается, что β1 = 0, то формально значимость оцененного коэффициента регрессии b1 проверяется с помощью
- 143. Для t-статистики проверяется нулевая гипотеза о равенстве ее нулю. Очевидно, t = 0 равнозначно b1 =
- 144. Гетероскедастичность Предпосылки МНК (условия Гаусса—Маркова) 2°. Дисперсия случайных отклонений εi постоянна: D(εi) = D(εj) = а
- 145. Выполнимость данной предпосылки называется гомоскедастичностъю (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
- 146. Данное условие подразумевает, что, несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть
- 149. Последствия гетероскедастичности При гетероскедастичности последствия применения МНК будут следующими. 1. Оценки коэффициентов по-прежнему останутся несмещенными и
- 150. 3. Дисперсии оценок будут рассчитываться со смещением. Смещенность появляется вследствие того, что не объясненная уравнением регрессии
- 151. 4. Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки
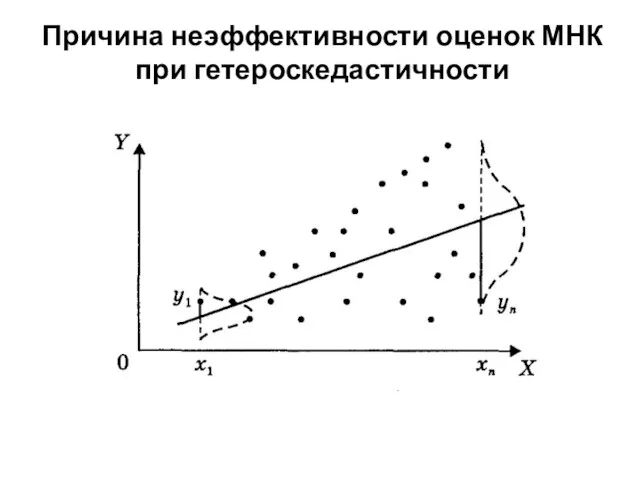
- 152. Причина неэффективности оценок МНК при гетероскедастичности
- 153. Обнаружение гетероскедастичности Не существует какого-либо однозначного метода определения гетероскедастичности. Рассмотрим наиболее популярные и наглядные: графический анализ
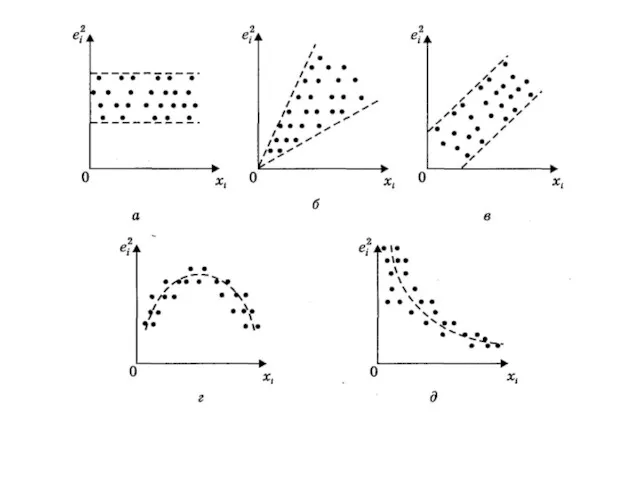
- 154. Графическое представление отклонений по оси абсцисс откладываются значения (хi) объясняющей переменной X (либо линейной комбинации объясняющих
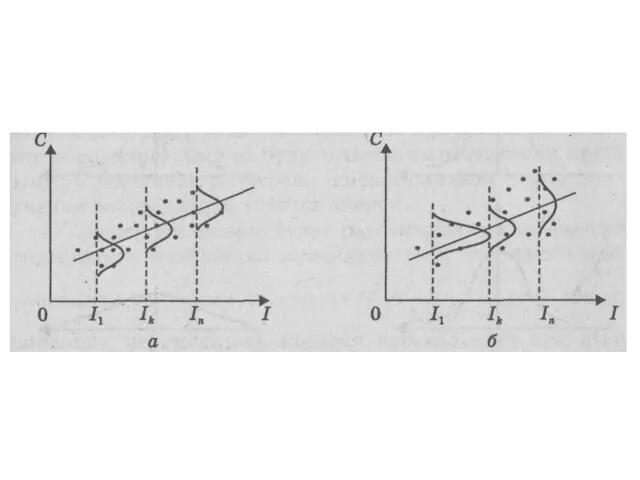
- 156. На рис. а все отклонения ei2 находятся внутри полуполосы постоянной ширины, параллельной оси абсцисс. Это говорит
- 157. Тест ранговой корреляции Спирмена Предположение Дисперсия отклонения будет либо увеличиваться, либо уменьшаться с увеличением значений X.
- 158. Ранжируем, то есть упорядочиваем по величинам значения xi и еi . Определяем коэффициент ранговой корреляции: где
- 159. Если коэффициент корреляции rхe для генеральной совокупности равен нулю, то статистика имеет распределение Стьюдента с числом
- 160. Следовательно, если наблюдаемое значение t-статистики, превышает tкp = ta/2,n-2 (определяемое по таблице критических точек распределения Стьюдента),
- 161. Если в модели регрессии больше чем одна объясняющая переменная, то проверка гипотезы может осуществляться с помощью
- 162. Тест Парка Критерий Парка дополняет графический метод некоторыми формальными зависимостями. Предполагается, что дисперсия σi2 = σ2(ei)
- 163. Прологарифмировав это выражение, получим: lnσi2 = lnσ2 +βlnхi +vi. Так как дисперсии σi2 обычно неизвестны, то
- 164. Критерий Парка включает следующие этапы: 1. Строится уравнение регрессии yi = b0 + b1xi + ei.
- 165. 4. Проверяется статистическая значимость коэффициента β уравнения регрессии на основе t-статистики . Если коэффициент β статистически
- 166. Отметим, что использование в критерии Парка конкретной функциональной зависимости может привести к необоснованным выводам (например, коэффициент
- 167. Тест Глейзера Тест Глейзера по своей сути аналогичен тесту Парка и дополняет его анализом других (возможно,
- 168. Зависимость моделируется следующим уравнением регрессии: Изменяя значения k, можно построить различные регрессии. Обычно k = ...,
- 169. Тест Голдфелда—Квандта Стандартное отклонение σi= σi(εi) пропорционально значению xi переменной X в этом наблюдении, т.е. ,
- 170. 2. Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей k, (п - 2k), k
- 171. Для сравнения соответствующих дисперсий строится следующая F-статистика: Здесь (k - т - 1) — число степеней
- 172. При сделанных предположениях относительно случайных отклонений построенная F-статистика имеет распределение Фишера с числами степеней свободы v1
- 173. Методы смягчения проблемы гетероскедастичности Метод взвешенных наименьших квадратов (ВНК)
- 174. Данный метод применяется при известных для каждого наблюдения значениях дисперсии случайных отклонений . В этом случае
- 175. Имеем уравнение парной регрессии Разделим обе части этого уравнения на известное Обозначив получим
- 176. При этом для vi выполняется условие гомоскедастичности. Следовательно, для преобразованной модели выполняются предпосылки МНК. В этом
- 177. Этапы ВНК 1. Значения каждой пары наблюдений (хi, yi) делят на известную величину среднего квадратического отклонения.
- 178. Действительно, наблюдения с меньшими дисперсиями отклонений будут более значимыми при оценке коэффициентов регрессии, чем наблюдения с
- 179. Дисперсии отклонений неизвестны Для применения ВНК необходимо знать фактические значения дисперсий σi2 отклонений. На практике такие
- 180. Например, может оказаться целесообразным предположить, что дисперсии σi2 отклонений εi; пропорциональны значениям xi или значениям xi2
- 181. Для случайных отклонений vi выполняется условие гомоскедастичности. Следовательно, для принятого уравнения регрессии применим обычный МНК. Таким
- 182. Дисперсии σi2 пропорциональны х2 В случае, если зависимость σi2 от хi целесообразнее выразить не линейной функцией,
- 183. Для отклонений vi будет выполняться условие гомоскедастичности. После определения по МНК оценок коэффициентов β0 и β1
- 185. Скачать презентацию





























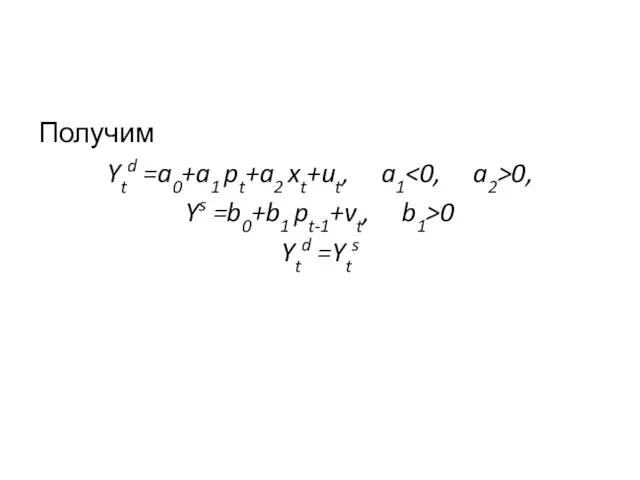






































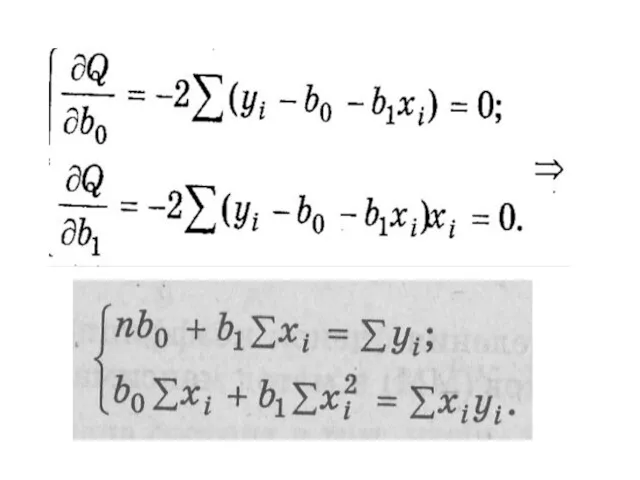
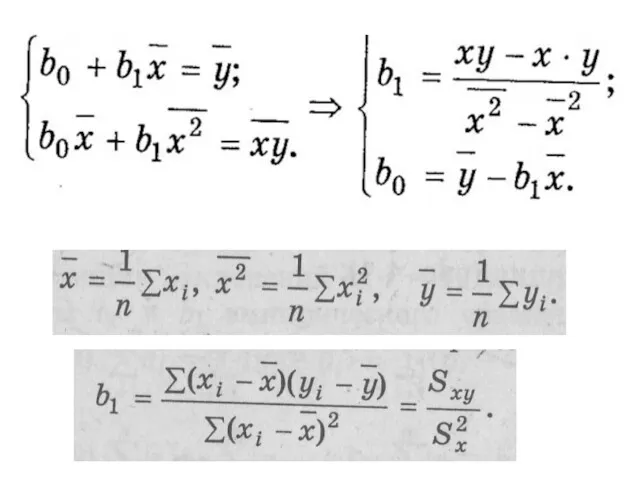


























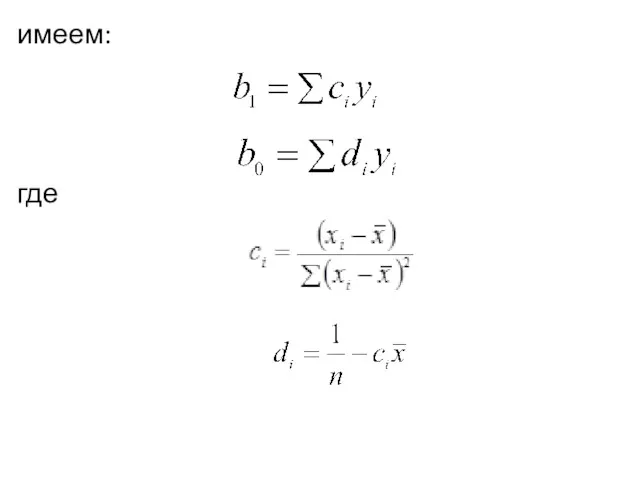



































































 Безработица
Безработица Презентация Деловой игры по Менеджменту для ссуза
Презентация Деловой игры по Менеджменту для ссуза Налог на доходы физических лиц (глава 23 НК РФ)
Налог на доходы физических лиц (глава 23 НК РФ)  Производство – основа экономики. 8 класс
Производство – основа экономики. 8 класс Риск в деятельности предприятия. Экономика предприятия
Риск в деятельности предприятия. Экономика предприятия Внешнеэкономическая политика Республики Беларусь
Внешнеэкономическая политика Республики Беларусь Залежність ціни авто від пробігу, об’єму двигуна та віку експлуатації
Залежність ціни авто від пробігу, об’єму двигуна та віку експлуатації Классификация и характеристика метода экспертных оценок
Классификация и характеристика метода экспертных оценок Роль олигополии в российской экономике
Роль олигополии в российской экономике Балансовые методы и макромоделирование в прогнозировании и стратегическом планировании организации. (Лекция 3)
Балансовые методы и макромоделирование в прогнозировании и стратегическом планировании организации. (Лекция 3) О реализации мер по обеспечению доступа негосударственных организаций к предоставлению услуг в социальной сфере
О реализации мер по обеспечению доступа негосударственных организаций к предоставлению услуг в социальной сфере Инфляция и ее показатели. Виды инфляции. Причины инфляции. Последствия инфляции. Издержки инфляции
Инфляция и ее показатели. Виды инфляции. Причины инфляции. Последствия инфляции. Издержки инфляции Mundell-Fleming Model with Partial International Capital Mobility
Mundell-Fleming Model with Partial International Capital Mobility Презентация: Семейный бюджет
Презентация: Семейный бюджет Теории инвестиций: сравнительный анализ
Теории инвестиций: сравнительный анализ Способы минимизации предпринимательских рисков
Способы минимизации предпринимательских рисков Информация, неопределенность, риск в экономике
Информация, неопределенность, риск в экономике Добыча нефти
Добыча нефти Распределение доходов
Распределение доходов Отечественный и зарубежный опыт мобилизации экономики
Отечественный и зарубежный опыт мобилизации экономики Производительность труда. Тема 2.3
Производительность труда. Тема 2.3 Основные направления современной зарубежной экономической мысли
Основные направления современной зарубежной экономической мысли Натуральное и товарное производство
Натуральное и товарное производство Стоимость ресурсов как метод регулирования природопользования
Стоимость ресурсов как метод регулирования природопользования Информационные технологии в экономике. Лекция 2
Информационные технологии в экономике. Лекция 2 Фирмы в экономике, или КАК разбогатеть
Фирмы в экономике, или КАК разбогатеть Основополагающие принципы налогообложения
Основополагающие принципы налогообложения Modeling of corruption in hierarchical control systems
Modeling of corruption in hierarchical control systems