Содержание
- 2. THERMODYNAMISC & STATISTICAL PHYSICS
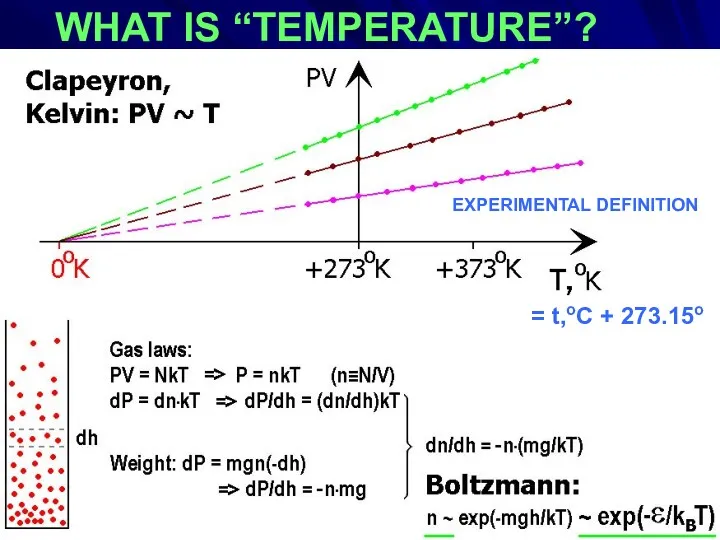
- 3. WHAT IS “TEMPERATURE”? EXPERIMENTAL DEFINITION : = t,oC + 273.15o EXPERIMENTAL DEFINITION
- 4. Benoît Paul Émile Clapeyron (1799 – 1864) William Thomson, 1st Baron Kelvin (1824 -1907) Ludwig Eduard
- 5. THEORY Closed system: energy E = const CONSIDER: 1 state of “small part” with ε &
- 6. COMPARE: Probability1(ε1) = Mt(E-ε1) / M(E) = exp[- ε1• (dSt/dE)|E/k] (GIBBS) and Probability1(ε1) = exp(-ε1/kBT) (BOLTZMANN)
- 7. Josiah Willard Gibbs (1839 –1903) Яков Григорьевич Синай, 1935 Abel Prize 2014 “…связь между порядком и
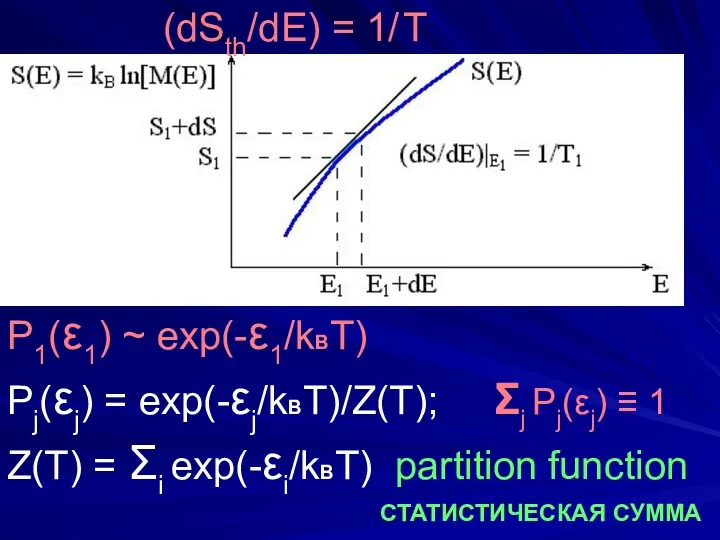
- 8. (dSth/dE) = 1/ T P1(ε1) ~ exp(-ε1/kBT) Pj(εj) = exp(-εj/kBT)/Z(T); Σj Pj(εj) ≡ 1 Z(T) =
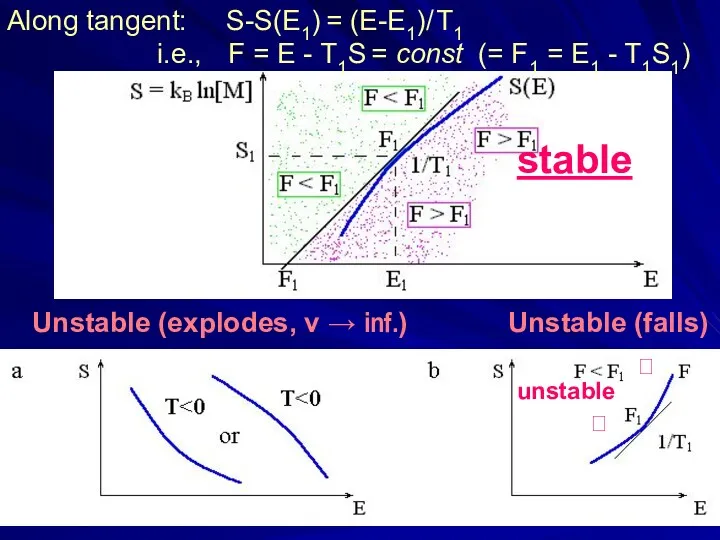
- 9. Unstable (explodes, v → inf.) Unstable (falls) stable ? unstable ? Along tangent: S-S(E1) = (E-E1)/
- 10. Separation of potential and kinetic energies in classic (non-quantum) mechanics: P(ε) ~ exp(-ε/kBT) // Classic: ε
- 11. IN THERMAL EQUILIBRIUM: TCOORD = TKIN = Touter We may consider further only potential energy: E
- 12. TRANSITIONS: THERMODYNAMICS
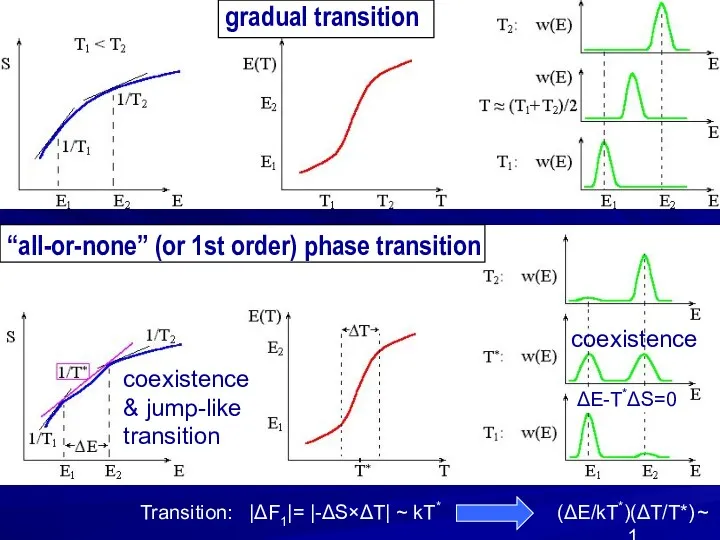
- 13. gradual transition “all-or-none” (or 1st order) phase transition coexistence & jump-like transition coexistence (ΔE/kT*)(ΔT/T*) ~ 1
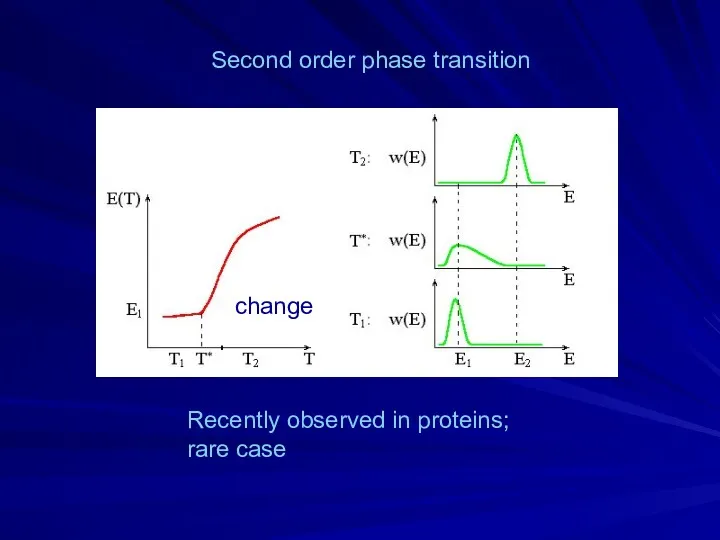
- 14. Second order phase transition change Recently observed in proteins; rare case
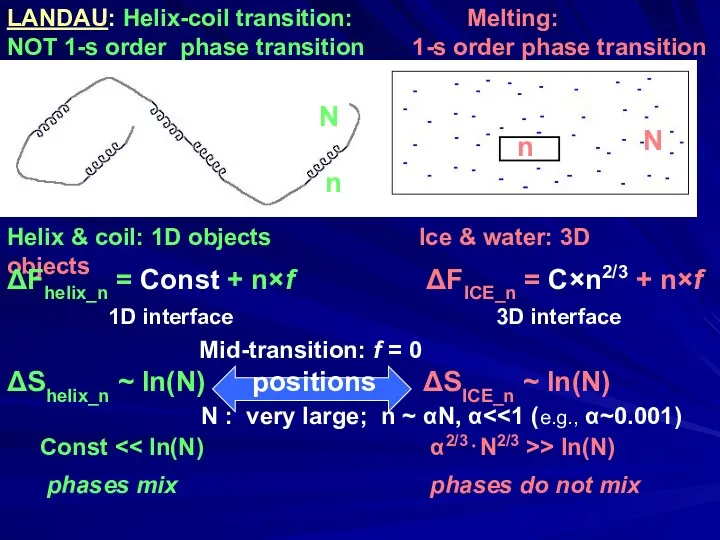
- 15. LANDAU: Helix-coil transition: Melting: NOT 1-s order phase transition 1-s order phase transition Helix & coil:
- 16. Лев Давидович Ландау (1908 - 1968) Нобелевская Премия 1962
- 17. TRANSITIONS: KINETICS
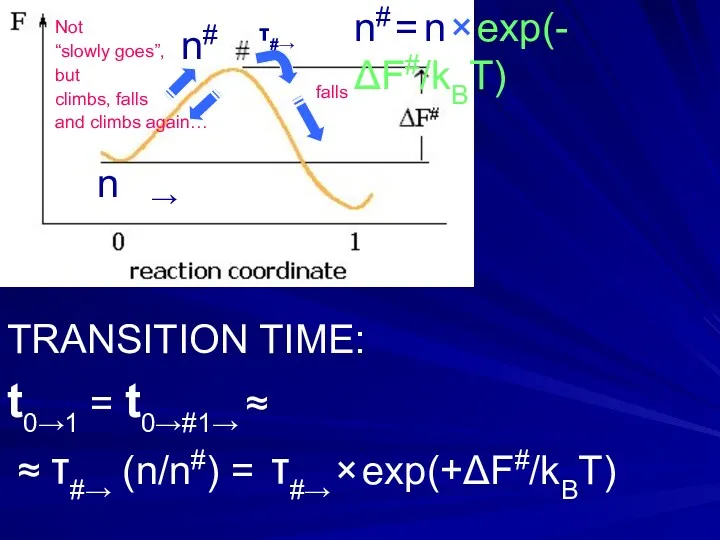
- 18. n# = n × exp(-ΔF#/kBT) n# n → TRANSITION TIME: t0→1 = t0→#1→ ≈ ≈ τ#→
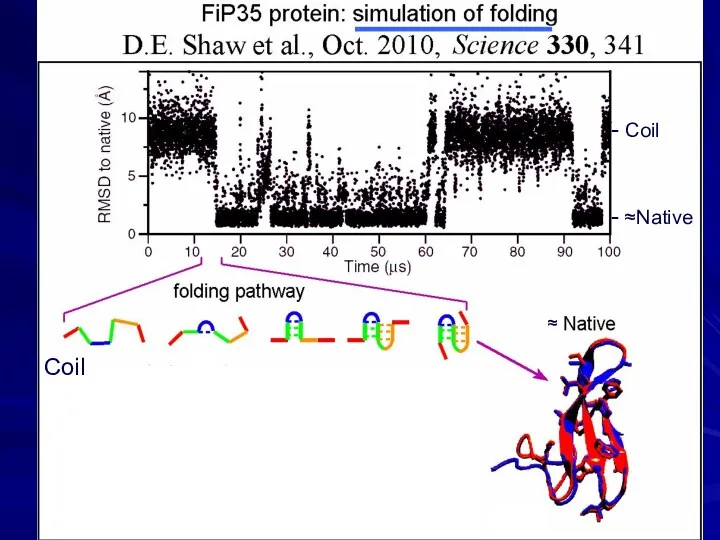
- 20. phase separation Coil - Coil - ≈Native ≈
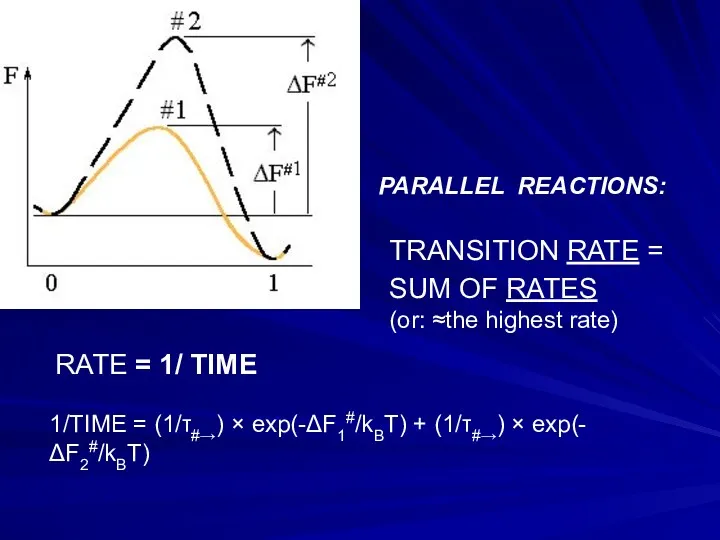
- 21. TRANSITION RATE = SUM OF RATES (or: ≈the highest rate) 1/TIME = (1/τ#→) × exp(-ΔF1#/kBT) +
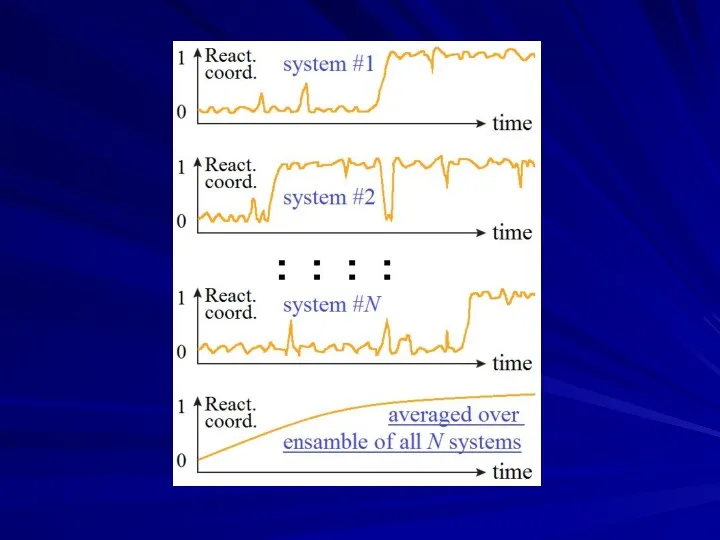
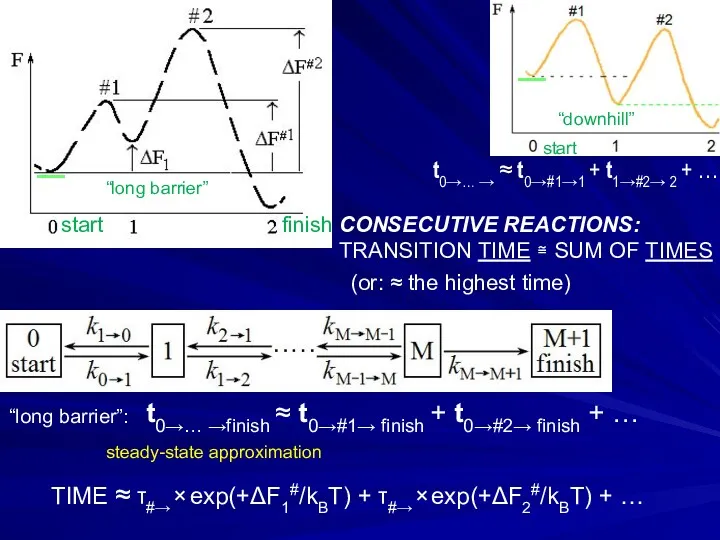
- 22. t0→… →finish ≈ t0→#1→ finish + t0→#2→ finish + … # # start _ CONSECUTIVE REACTIONS:
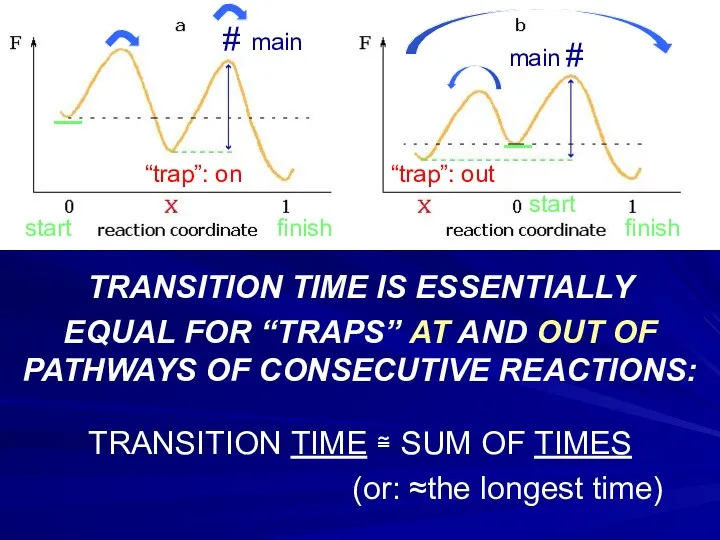
- 23. _ _ TRANSITION TIME IS ESSENTIALLY EQUAL FOR “TRAPS” AT AND OUT OF PATHWAYS OF CONSECUTIVE
- 24. DIFFUSION: KINETICS
- 25. Mean kinetic energy of a particle: ~ kBT = Σj Pj(εj) ∙ εj v2 = (vX2)+(vY2)+(vZ2)
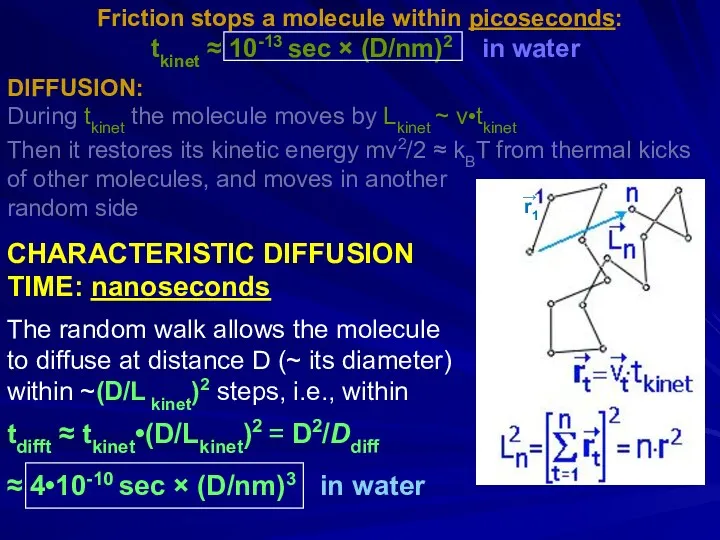
- 26. Friction stops a molecule within picoseconds: m(dv/dt) = -(3πDη)v [Stokes law], or m(dv/dt) = -(kBT/Ddiff)v [Einstein-Stokes]
- 27. Friction stops a molecule within picoseconds: tkinet ≈ 10-13 sec × (D/nm)2 in water DIFFUSION: During
- 28. The End
- 29. For “small part”: Pj(εj) = exp(-εj/kBT)/Z(T); Z(T) = Σj exp(-εj/kBT) Σj Pj(εj) = 1 E(T) =
- 30. Thermostat: Tth = dEth/dSth “Small part”: Pj(εj,Tth) ~ exp(-εj/kBTth); E(Tth) = Σj εj Pj(εj,Tth) S(Tth) =
- 31. Along tangent: S-S(E1) = (E-E1)/ T1 i.e., F = E - T1S = const (= F1
- 32. Separation of potential energy in classic (non-quantum) mechanics: P(ε) ~ exp(-ε/kBT) Classic: ε = εCOORD +
- 33. P(εKIN+εCOORD) ~ exp(-εCOORD/kBT)•exp(-εKIN/kBT) P(εCOORD) = exp(-εCOORD/kBT) / ZCOORD(T) ZCOORD(T) = ΣCexp(-εC/kBT): depends ONLY on coordinates P(εKIN)
- 35. Скачать презентацию



![COMPARE: Probability1(ε1) = Mt(E-ε1) / M(E) = exp[- ε1• (dSt/dE)|E/k]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/203710/slide-5.jpg)















 Ремонт автомобилей. Ремонт кузовов и кабин. (Тема 4.11)
Ремонт автомобилей. Ремонт кузовов и кабин. (Тема 4.11) Статическое электричество, защита от него. Молниеотвод
Статическое электричество, защита от него. Молниеотвод Основные положения электромагнитной теории Максвелла
Основные положения электромагнитной теории Максвелла Механические передачи. Виды механических передач
Механические передачи. Виды механических передач “Положение тела в пространстве”
“Положение тела в пространстве”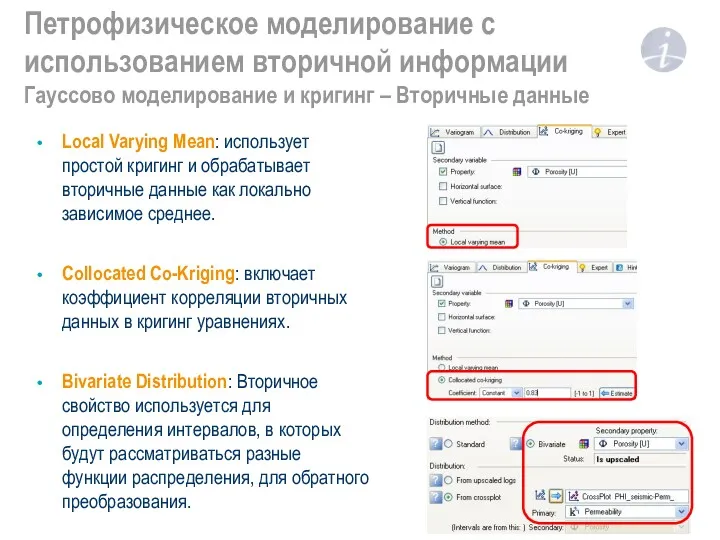 Петрофизическое моделирование с использованием вторичной информации. Гауссово моделирование и кригинг – Вторичные данные
Петрофизическое моделирование с использованием вторичной информации. Гауссово моделирование и кригинг – Вторичные данные Строение коробки-автомат с гидротрансформатором
Строение коробки-автомат с гидротрансформатором Модель атома Резерфорда-Бора
Модель атома Резерфорда-Бора Жарықтың интерференциясы
Жарықтың интерференциясы Обприскувачі. Лабораторна робота
Обприскувачі. Лабораторна робота На чем основано воздухоплавание
На чем основано воздухоплавание презентации к урокам
презентации к урокам Әр түрлі иондаушы сәулелер көздері түрлерінің заттармен өзара әсерлесуі
Әр түрлі иондаушы сәулелер көздері түрлерінің заттармен өзара әсерлесуі Механическая работа
Механическая работа Дидактический пакет по проектированию образовательного процесса по физике в 10 кл., тема : Молекулярная физика. Термодинамика
Дидактический пакет по проектированию образовательного процесса по физике в 10 кл., тема : Молекулярная физика. Термодинамика Введение в квантовую физику. (Лекция 13)
Введение в квантовую физику. (Лекция 13) Закон Ома для участка цепи и полной цепи
Закон Ома для участка цепи и полной цепи Неньютоновские жидкости
Неньютоновские жидкости Кинематика
Кинематика Шкала электромагнитных волн. Виды, свойства и применение
Шкала электромагнитных волн. Виды, свойства и применение Электромагнитная природа света
Электромагнитная природа света Разряды в жидких и твердых диэлектриках. Электрические характеристики внутренней изоляции. (Лекция 6)
Разряды в жидких и твердых диэлектриках. Электрические характеристики внутренней изоляции. (Лекция 6)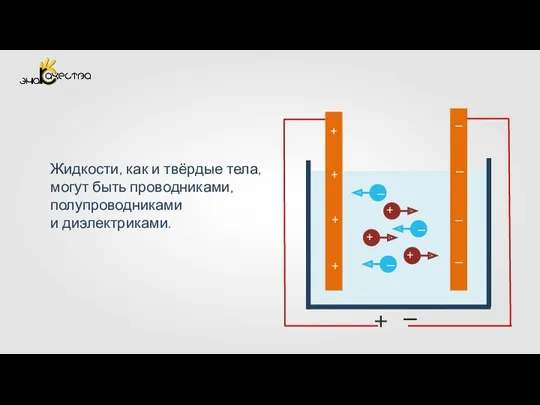 Электрический ток в жидкостях. Закон электролиза
Электрический ток в жидкостях. Закон электролиза Оптика. Способы передачи воздействий
Оптика. Способы передачи воздействий Нанотехнології в нашому житті. Загроза цивілізації, або стрибок у майбутнє
Нанотехнології в нашому житті. Загроза цивілізації, або стрибок у майбутнє Плотность вещества. Фронтальный опрос
Плотность вещества. Фронтальный опрос Волновые процессы в механике. Лекция 7
Волновые процессы в механике. Лекция 7 Этапы становления научной дисциплины Электротехника
Этапы становления научной дисциплины Электротехника