Содержание
- 2. Динамика - раздел теоретической механики, в котором изучаются движение тел под действием приложенных сил
- 3. Законы динамики.
- 4. 1) І-ый закон Ньютона Если на тело не действуют силы, то оно находится либо в состоянии
- 5. 2) ІІ-ой закон Ньютона Ускорение движения тела пропорционально действующей на него силе
- 6. 3) ІІІ-ий закон Ньютона Каждому действию соответствует равное и противоположно направленное противодействие
- 7. 4) Принцип суперпозиции. Если на тело действует несколько сил, то ускорение движения тела будет пропорционально одной
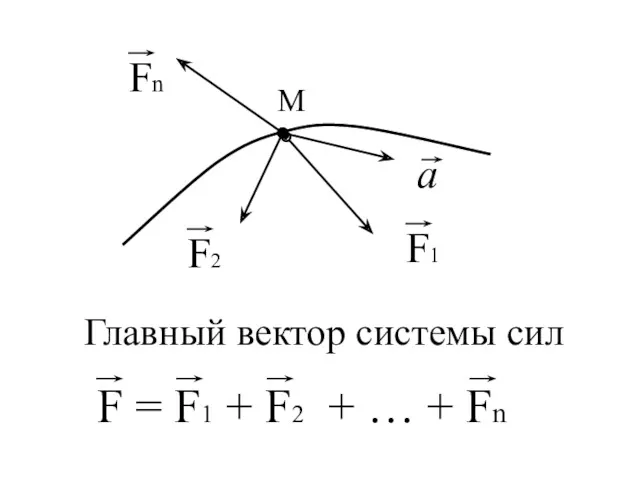
- 8. Главный вектор системы сил
- 9. Дифференциальные уравнения движения точки.
- 10. Дифференциальные уравнения движения точки в декартовой системе координат.
- 12. ox: oy: oz: F1x +…+ Fnx F1y +…+ Fny F1z +…+ Fnz Проецируем векторное равенство на
- 13. ax = ay = az = Проекции ускорений:
- 14. Σ Fkx Σ Fky Σ Fkz дифференциальные уравнения движения точки в декартовой с. к.
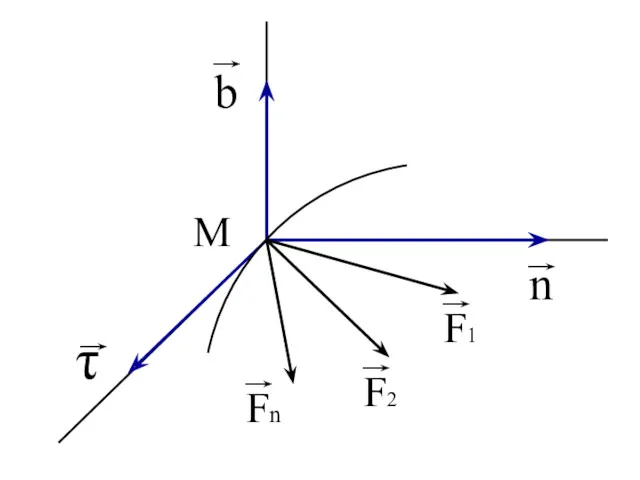
- 15. Дифференциальные уравнения движения точки в осях естественного трехгранника.
- 17. Запишем ІІ-ой закон Ньютона:
- 18. Проецируем это равенство на оси естественного трехгранника:
- 19. 0 - тангенсальная составляющая - нормальная составляющая - т.к. вектор ускорения лежит в соприкасающейся плоскости Проекции
- 20. дифференциальные уравнения движения точки в осях естественного трехгранника
- 21. Задачи динамики
- 22. Прямая задача По известной массе, известному закону движения требуется определить результирующую силу, действующую на тело.
- 23. Дано: m x = x(t) y = y(t) z = z(t) Найти: F - ?
- 24. Решение: Fx Fy Fz F = - модуль силы
- 25. Направление задается направляющими косинусами:
- 26. Обратная задача По известной массе, известным силам, известным начальным условиям требуется определить закон движения.
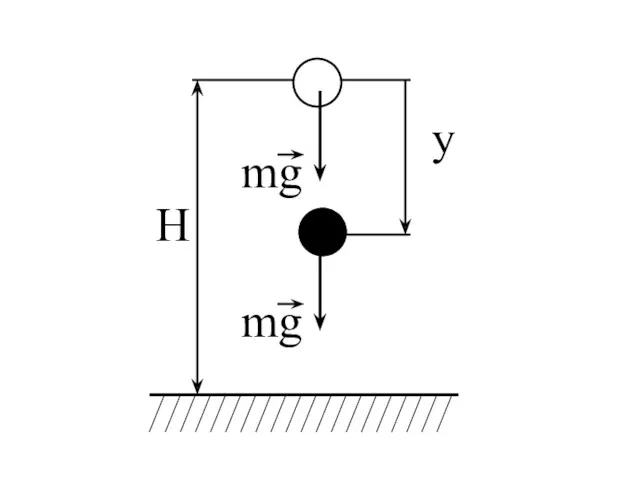
- 28. Для того, чтобы получить закон движения, необходимо дважды проинтегрировать каждое уравнение, используя начальные условия (но не
- 30. Σ Fky mg g Vy , g y - ? Запишем закон движения в проекции на
- 31. Vy = g t g t y = =>
- 32. Динамика системы
- 33. Внешние силы Внутренние силы - силы, действующие на тела данной системы со стороны тел, не входящих
- 34. Главный вектор внутренних сил системы равен нулю. Главный момент внутренних сил системы равен нулю.
- 35. Масса. Центр масс.
- 36. Масса системы М = Центр масс системы - сумма масс тел, входящих в систему. - геометрическая
- 37. Для того, чтобы получить координаты центра масс, надо спроецировать векторное равенство на оси.
- 38. xc = zc = yc =
- 39. Дифференциальные уравнение движения системы
- 42. Теорема об изменении количества движения
- 43. Запишем ІІ-ой закон Ньютона для точки: Получим теорему об изменении количества движения точки в дифференциальной форме:
- 44. - количество движения системы - сумма количеств движений точек, входящих в систему Распишем выражение и поменяем
- 45. => - количество движения системы - произведение массы системы и скорости ее центра масс
- 46. Запишем ІІ-ой закон Ньютона для системы точек: Меняя порядок суммирования и дифференцирования получим: Теорема об изменении
- 47. Первая производная по времени от вектора количества движения системы равна главному вектору внешних сил
- 48. Следствия : 1) 2) Если главный вектор внешних сил системы равен нулю, то тело покоится или
- 49. Fxe Fye Fze
- 50. Теорема о движении центра масс системы
- 51. Эта формула гласит: Центр масс системы движется как материальная точка, к которой приложены все силы, действующие
- 52. Следствия : 1) 2) Внутренними силами нельзя изменить движение центра масс системы. Если главный вектор внешних
- 53. 3) m ac x = Fxe Fye Fze m ac y = m ac z =
- 54. Теорема об изменении момента количества движения
- 55. По ІІ закону ньютона Пусть r - радиус-вектор, определяющий положение точки относительно какой либо системы координат.
- 56. Обозначим: - момент количества движения точки относительно точки О - момент силы F относительно точки О
- 57. Момент количества движения системы определяется как векторная сумма моментов количества движения точек, входящих в систему.
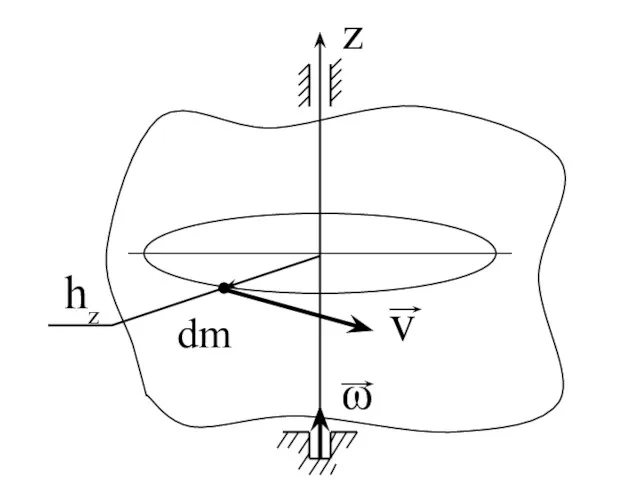
- 58. Момент количества движения твердого тела, вращающегося вокруг неподвижной оси (кинетический момент)
- 60. v = ωz·hz v dm = ωz hz dm v dm hz = ωz hz2 dm
- 61. Kz = I = Kz = Iz ·ωz - момент инерции тела относительно оси (осевой момент
- 62. Моменты инерции
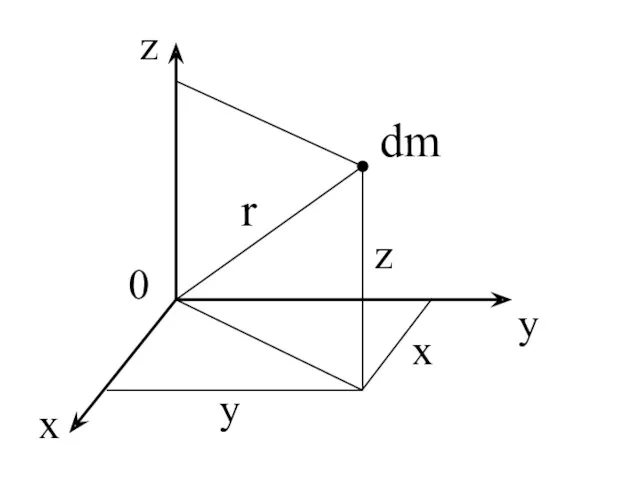
- 64. Осевой момент инерции точки Izk = dm·hz2 = dm(x2 + y2) Iz = - для точки
- 65. Полярный момент инерции точки I0k = dm·r 2 = dm(x2 + y2 + z2) I0 =
- 66. Центробежные моменты инерции - произведение массы точки на координаты, стоящие в индексе
- 67. Ixy = Ixz = Iyz = - для тела Ixy = dm·x ·y Ixz = dm·x
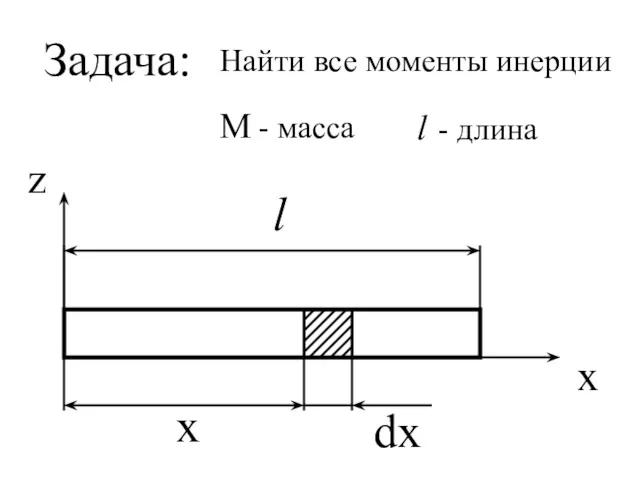
- 68. Задача: М - масса l - длина Найти все моменты инерции
- 69. dm = Iz = Ic = Масса кусочка dx : - момент инерции относительно оси z
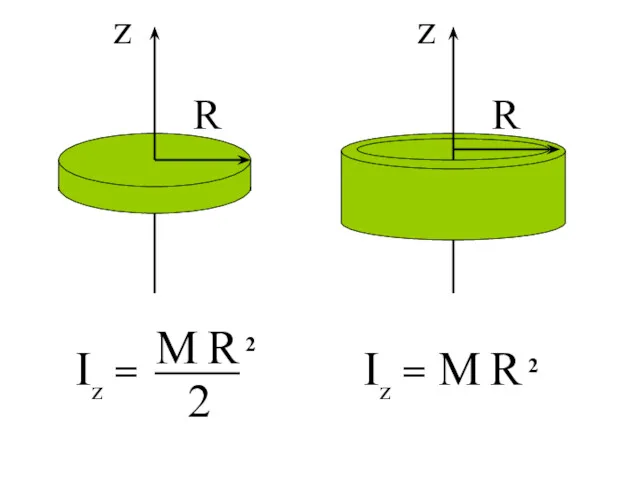
- 70. Iz = Iz = M R 2
- 71. Теорема об изменении момента количества движения точки = M0e
- 72. Производная по времени от вектора момента количества движения точки равна моменту внешних сил относительно той же
- 73. . . . . . . . . . . . . . . .
- 74. Почленно сложим уравнения системы:
- 75. Следствия : 1) 2) Внутренними силами нельзя изменить момент количества движения системы. Если главный момент внешних
- 76. 3) Mxe Mze Mye Если проекция главного момента внешних сил на какую-либо ось равна нулю, то
- 77. Дифференциальное уравнение движения твердого тела относительно неподвижной оси
- 78. Mze Mze Mze Kz = Iz ·ωz
- 79. Работа силы
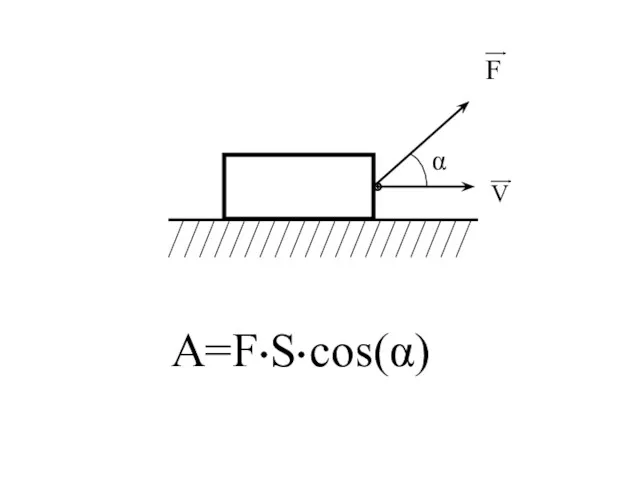
- 80. Прямолинейное перемещение тела.
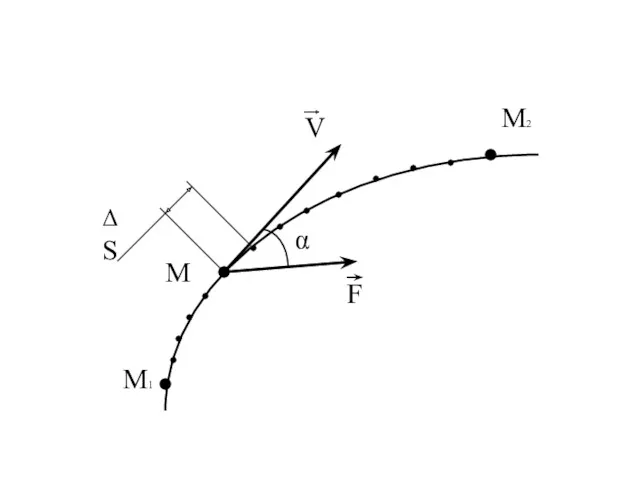
- 82. Перемещение тела по кривой.
- 83. Если точка перемещается по кривой и сила изменяется, то для того чтобы найти работу силы, произведенную
- 84. Δ S
- 85. Тогда работа , произведенная силой на k-ом участке определится как: Ak = Вся работа на участке
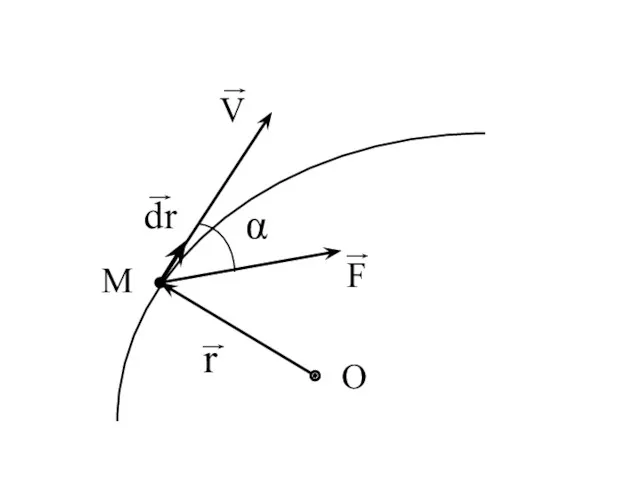
- 86. A1,2 = Элементарная работа: Работа определяется точно криволинейным интегралом:
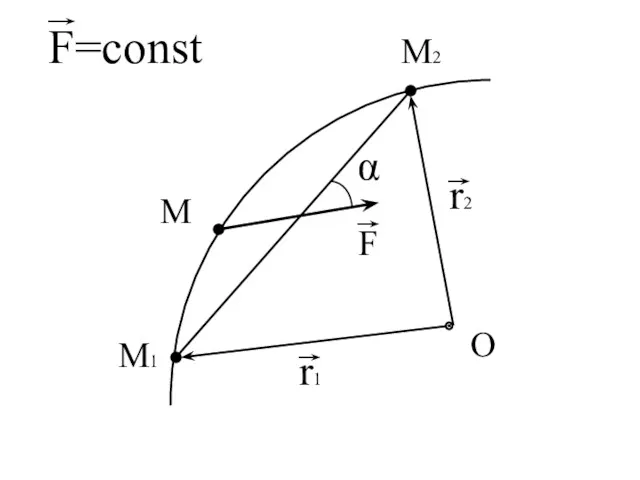
- 89. Работа силы, постоянной по величине и направлению.
- 91. A1,2 = A1,2 = где: S = M1M2 Тогда работа равна:
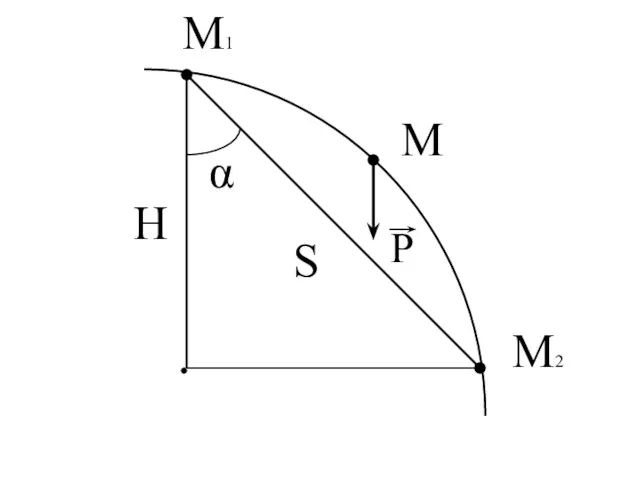
- 92. Работа силы тяжести.
- 94. A1,2 = Изменение положения тела по высоте определяется: Тогда работа на участке равна: Если тело опускают
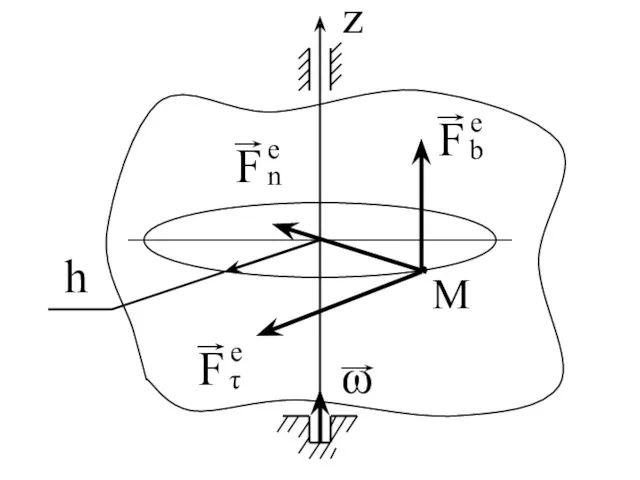
- 95. Работа силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси.
- 97. h - кратчайшее расстояние от точки до оси вращения. Сила F разложена на составляющие:
- 98. Полная работа: Элементарная работа силы Fτe : Работа силы Fbe также равна нулю.
- 99. Если: - работа момента
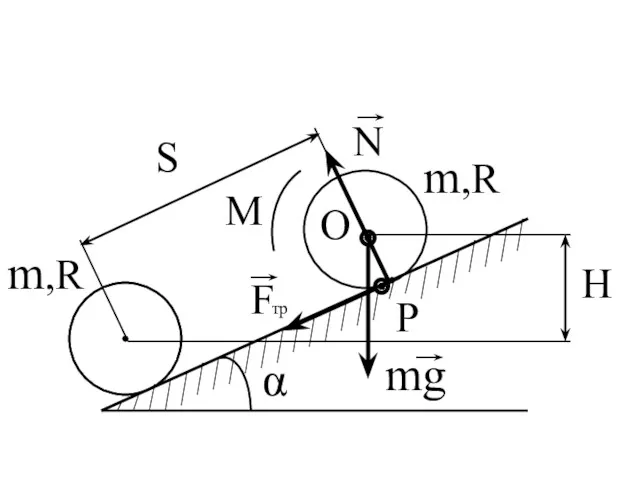
- 100. Пример Центр тяжести однородного колеса поднимается на высоту h, под действием момента М Найти работу внешних
- 101. H S
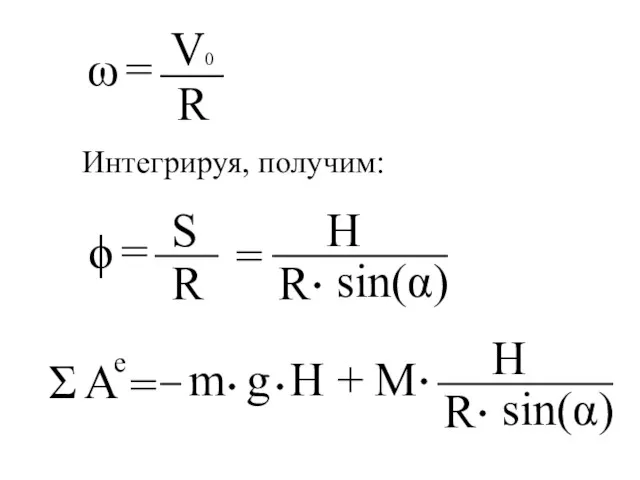
- 102. M = const ; т. P - МЦС Работы силы трения и силы реакции опоры равны
- 103. ω = ϕ = Интегрируя, получим:
- 104. Кинетическая энергия
- 105. Кинетическая энергия точки
- 106. Для точки второй закон Ньютона выглядит так:
- 107. d'A T = - Теорема об изменении кинетической энергии точки в дифференциальной форме. Заменим отношение дифференциалов
- 108. T = Кинетическая энергия системы определяется как сумма кинетических энергий точек, входящих в систему.
- 109. Кинетическая энергия системы. (Теорема Кёнига)
- 111. 01x1y1z1 - неподвижная система координат Система координат 02x2y2z2 перемещается поступательно.
- 112. Tr = Дифференцируем уравнение по времени. - кинетическая энергия системы относительно подвижной системы координат
- 113. Tr T =
- 114. Дифференцируем повремени:
- 115. T = Tr 0 Совместим начало подвижной системы координат с центром масс системы:
- 116. T = Tr Кинетическая энергия системы равна сумме кинетической энергии поступательного движения центра масс системы и
- 117. Кинетическая энергия твёрдого тела
- 118. При поступательном движении: T = T = T = Кинетическая энергия системы определяется - полупроизведение массы
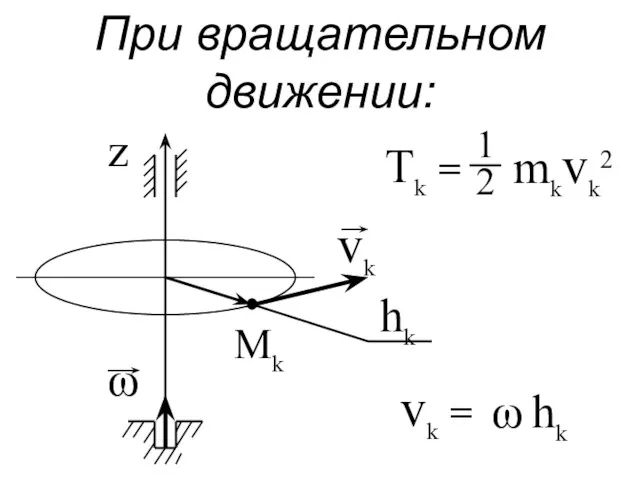
- 119. При вращательном движении: Tk = vk = ω hk
- 120. Tk = T = Σ mk hk2 = Iz T = Кинетическая энергия системы: - момент
- 121. При плоскопараллельном движении: T = Tr T = кинетическая энергия определяется по формуле Кёнига -
- 122. Пример Дано: r, m-радиус и масса однородного диска. Vc- скорость центра масс диска. Диск катится без
- 124. Теорема об изменении кинетической энергии системы
- 125. Пусть система состоит из n-материальных точек. Делим все силы, действующие на систему, на внешние и внутренние
- 126. dA1e + dA1i dAne + dAni . . . . . . . . . .
- 127. dAe + dAi dT = dAe + dAi - теорема об изменении кинетической энергии системы в
- 128. T - T0 = Ae + Ai Если под действием внешних и внутренних сил системы она
- 129. Изменение кинетической энергии системы при перемещении ее из начального положения в конечное равна сумме работ внешних
- 130. Принцип Даламбера или Принцип кинетостатики
- 131. Для каждой k-ой точки можно записать ІІ-ой закон Ньютона: Система состоит из n-точек. Разделяем силы на
- 132. 0 Тогда: т.е. сумма внешних, внутренних сил системы и силы инерции равна нулю. 0 Сумма главных
- 133. 0 0 К каждой точке системы проведем соответствующий радиус- вектор. Тогда:
- 134. 0 0 M0e - главный момент внешних сил M0i - главный момент внутренних сил M0и -
- 135. Главный момент и главный вектор сил инерции
- 136. 0 m - Теорема о движении центра масс системы Главный вектор сил инерции определяется как произведение
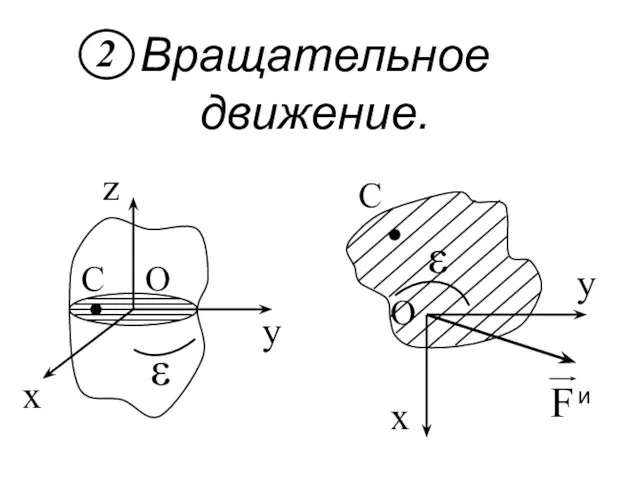
- 137. Вращательное движение.
- 138. M0zи = K0z = I0z· M0zи = – I0z·ε Подставим и получим: В проекции на ось
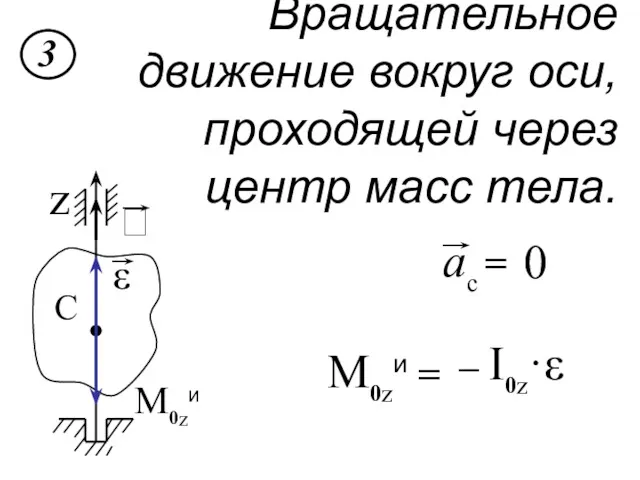
- 139. Вращательное движение вокруг оси, проходящей через центр масс тела. 0 M0zи = – I0z·ε M0zи
- 140. Плоскопараллельное движение. Mczи = – Icz·ε В этом случае присутствуют и главный вектор и главный момент
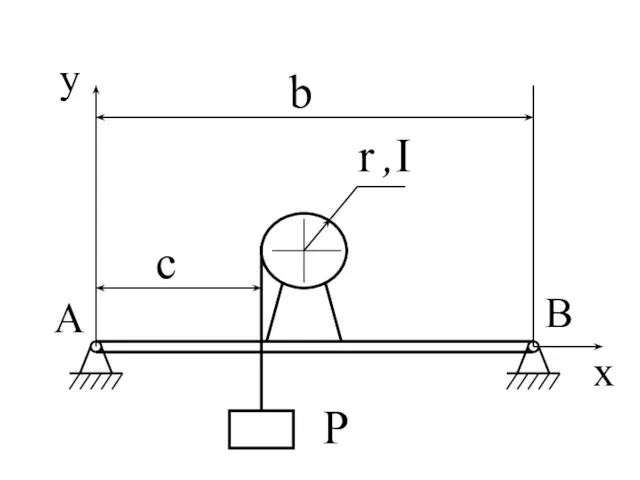
- 141. P r ,I
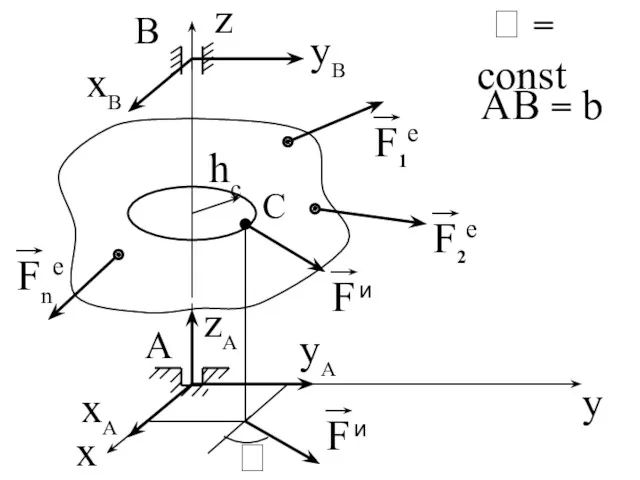
- 143. Динамические реакции твердого тела, вращающегося вокруг неподвижной оси
- 144. = const AB = b
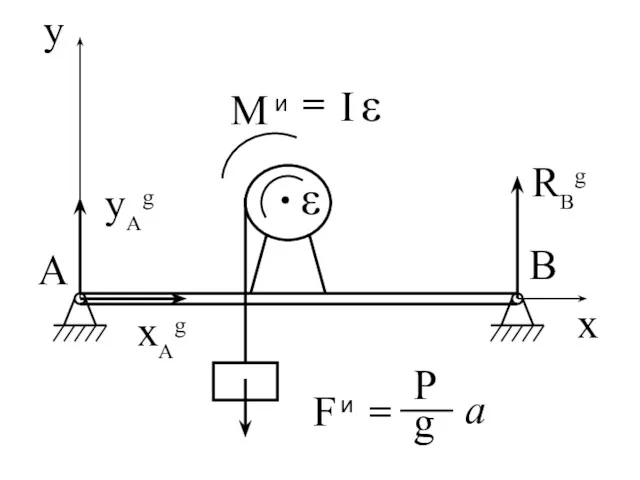
- 145. hc - кратчайшее расстояние от центра масс до оси вращения. Используем принцип Даламбера. Составляем условие равновесия
- 146. Мxe, Мye, Мze - алгебраические суммы проекций моментов внешних сил на оси x,y,z; Мxи, Мyи -
- 147. xA + xB + Fxe + Fxи = 0 zA + Fze + Fzи = 0
- 148. ac = 2 hc Fxи = M 2 hc· cos() = M 2
- 149. x y z Fx Fy Fz Для одной точки mx (Fkи) - момент относительно оси x
- 150. mx (Fkи) = y Fz – z Fy my (Fkи) = z Fx – x Fz
- 151. Mxи = – ( Σ mk y k z k) 2 = Mxи = (
- 152. xA + xB + Fxe + M 2 xc = 0 zA + Fze =
- 153. Iyz = Ixz = 0, Слагаемые, в которых присутствует угловая скорость будут являться динамическими реакциями. Эти
- 154. Аналитическая механика
- 155. Аналитическая механика Методы аналитической механики позволяют рассматривать системы без учета реакций идеальных связей
- 156. Виртуальные (возможные) перемещения
- 157. Классификация связей
- 158. 1) Удерживающие связи (x2–x1)2 + (y2–y1)2 + (z2–z1)2 = l2 Неудерживающие связи (x2–x1)2 + (y2–y1)2 +
- 159. 2) Стационарные связи Нестационарные связи 3) Голономные связи Неголономные связи В уравнении нет зависимости от времени.
- 160. Пример: 0 Неголономная нестационарная неудерживающая связь
- 161. f ( x, y, z, t ) = 0 M0 ( x0, y0, z0 ) x
- 162. f (x0 + x, y0 + y, z0 + z, t ) = = f (x0,
- 163. 0 Учитываем, что первое слагаемое по условию равно нулю. Тогда уравнение справедливо когда сумма 2-го, 3-го,
- 164. 0 т. е. => = 90°
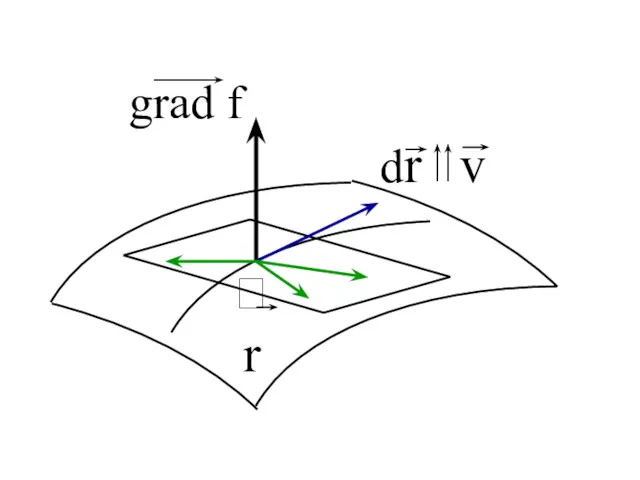
- 166. Виртуальное перемещение - мнимое, происходящее в фиксированный момент времени, малое, не нарушающее уравнения связей с учетом
- 167. Виртуальная работа А = Дадим системе виртуальное перемещение и подсчитаем элементарную работу, произведенную силами на этих
- 168. Идеальные связи 0 Принцип виртуальных перемещений - связи, работа реакций которых на любом виртуальном перемещении равна
- 169. Для того, чтобы система, подчиненная идеальным стационарным удерживающим связям, находилась в равновесии, необходимо и достаточно, чтобы
- 170. Необходимость: 0 , v k = 0 0 0 0 => 0
- 171. Достаточность: 0 0 0 0 =>
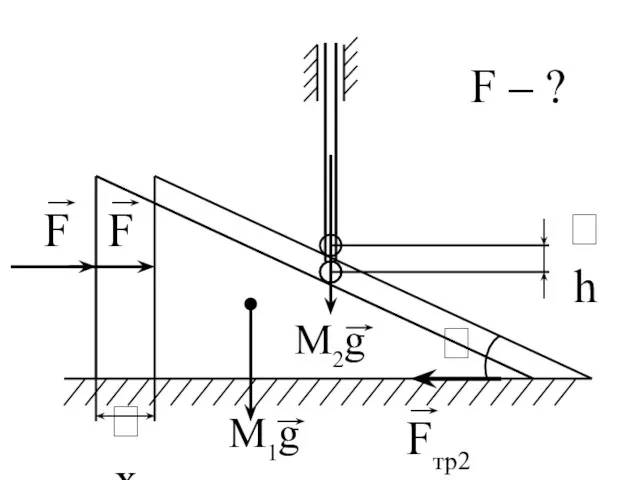
- 172. Определить величину силы F, необходимую для равновесия. Решить, используя принцип виртуальных перемещений. Задача.
- 173. h x F – ?
- 174. 0 – F x – Fтр x + M2 g h = 0 h = x
- 175. F = M2 g tg – f (M2 + M2) g F x – Fтр
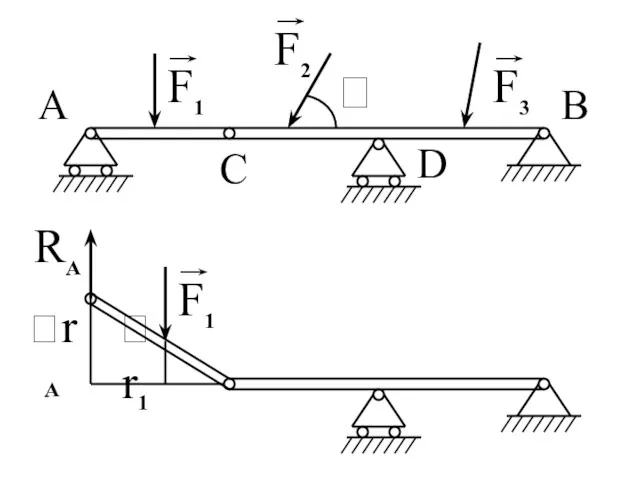
- 176. Использование принципа виртуальных перемещений для определения реакций связей
- 178. Общее уравнение динамики
- 179. Пусть система, состоящая из n-точек и подчиненная удерживающим голономным идеальным связям, движется. Освобождаемся от связей и
- 180. 0 0 Даем системе виртуальное перемещение. Каждая точка переместится на rk - по определению идеальных связей.
- 181. 0 - общее уравнение динамики. При движении материальной системы, подчиненной идеальным удерживающим голономным связям, сумма работ
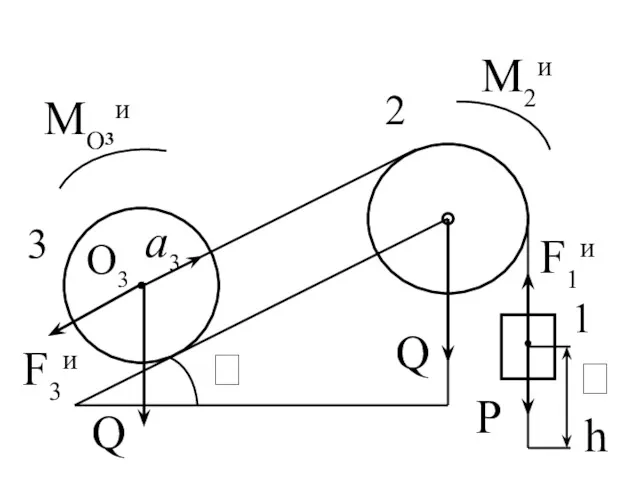
- 182. Пример: P, Q, Q, – дано a3 – найти
- 183. O3
- 184. УРАВНЕНИЕ ЛАГРАНЖА II РОДА ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ: => - s- число степеней свободы
- 185. -
- 186. -ОБОБЩЕННАЯ СИЛА **
- 187. *
- 188. Изменим порядок дифференцирования
- 189. Вносим под знак частной производной
- 192. Изобразить на чертеже все активные силы, действующие на систему. Реакции идеальных связей можно не изображать. Силы
- 193. Вычислить кинетическую энергию системы, выразив ее через обобщенные координаты и скорости Найти обобщенные силы системы Выполнить
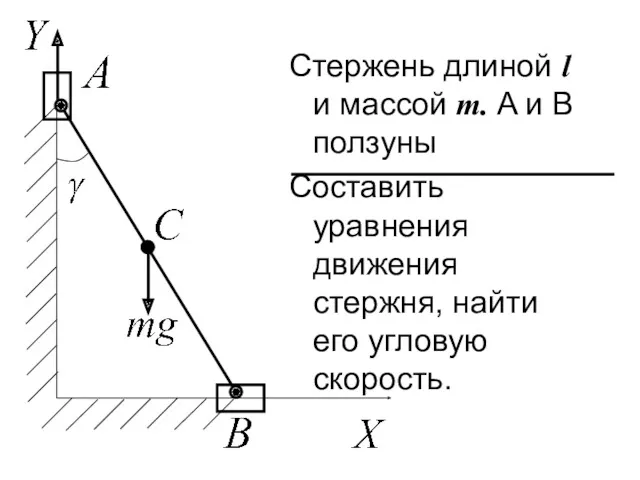
- 194. Стержень длиной l и массой m. A и B ползуны Составить уравнения движения стержня, найти его
- 195. Силы – mg Степень свободы – 1 обобщенная координата
- 196. 4) Обобщенные силы Потенциальная энергия
- 198. До множим уравнение
- 200. Интегрируем
- 201. Если в начальный момент времени
- 203. Скачать презентацию










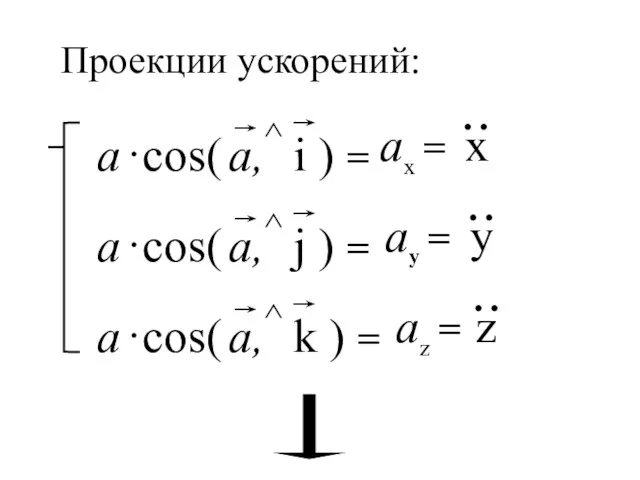









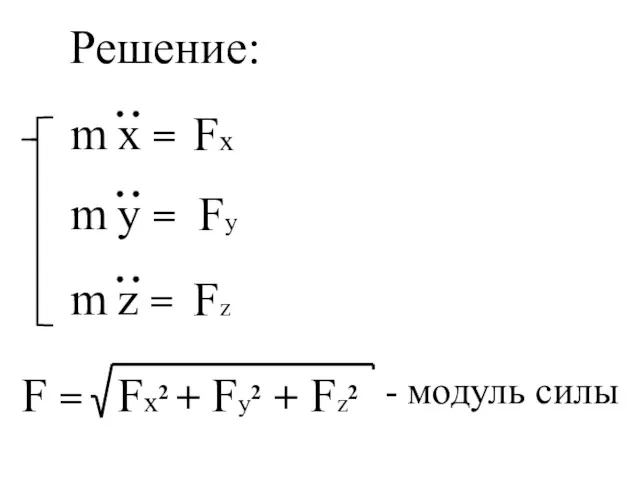


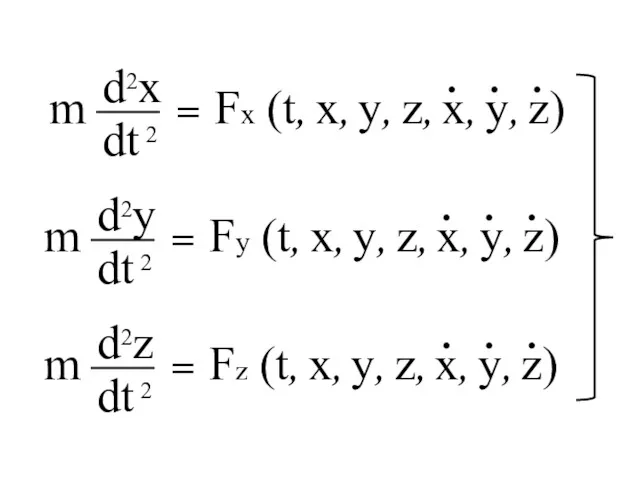

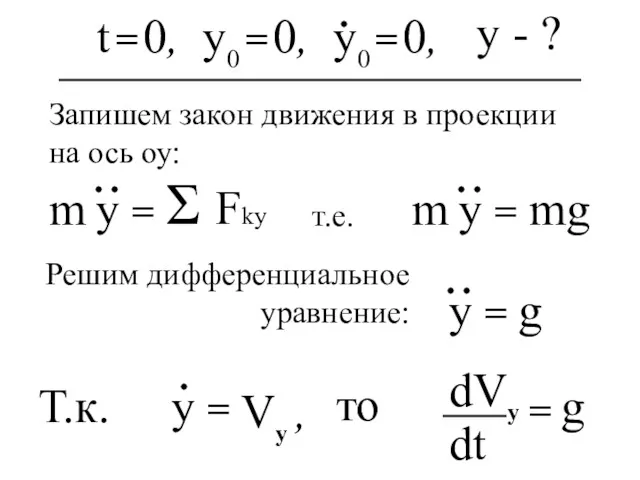
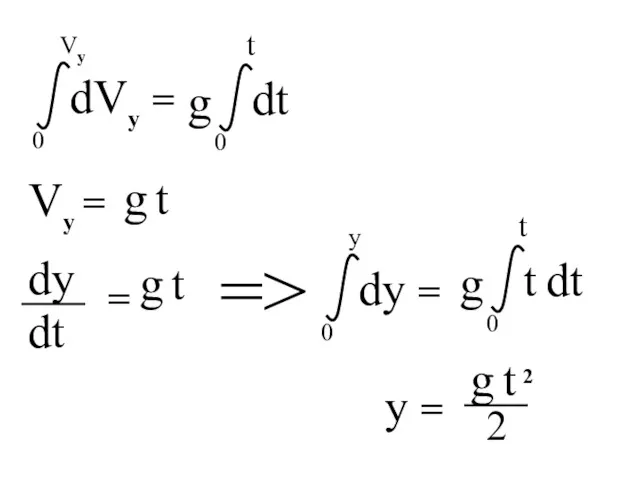






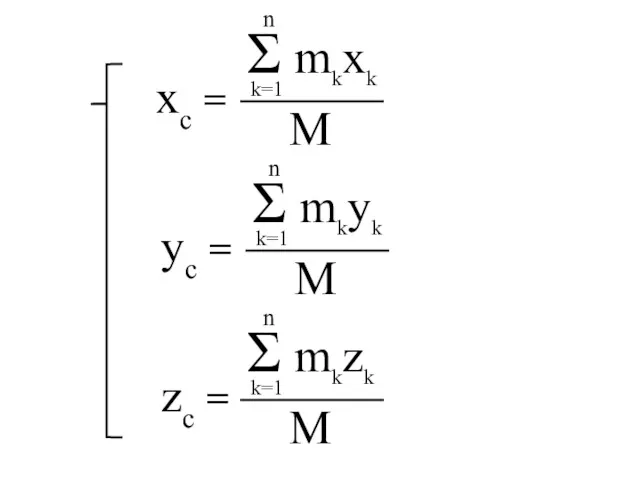










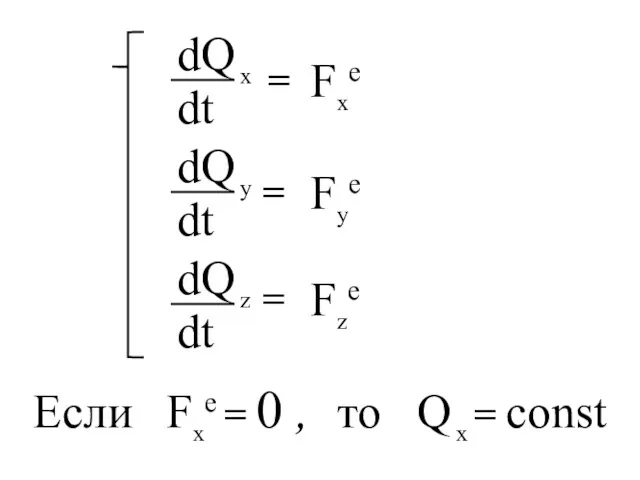















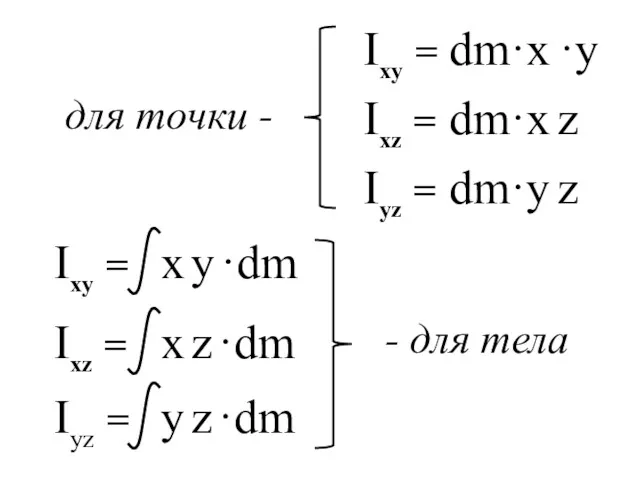



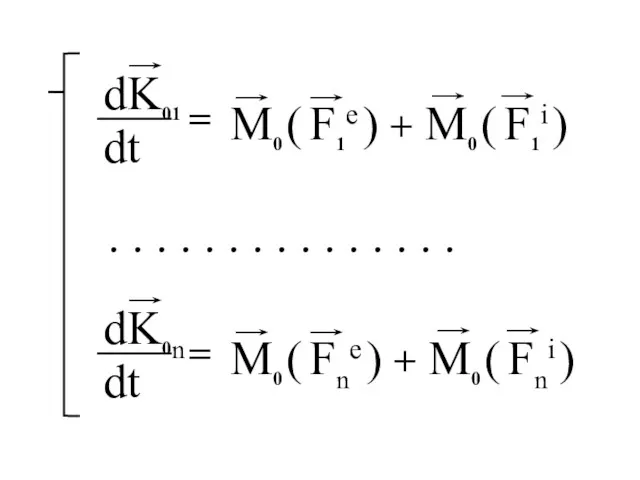




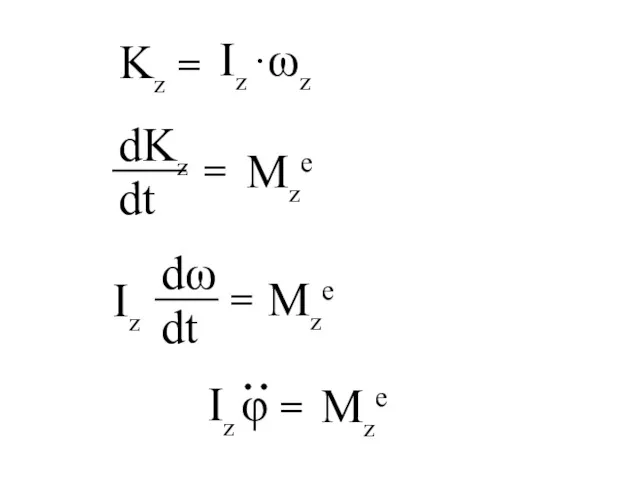








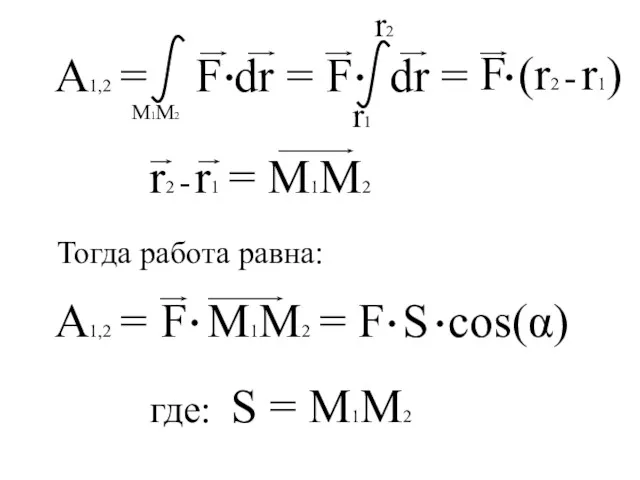





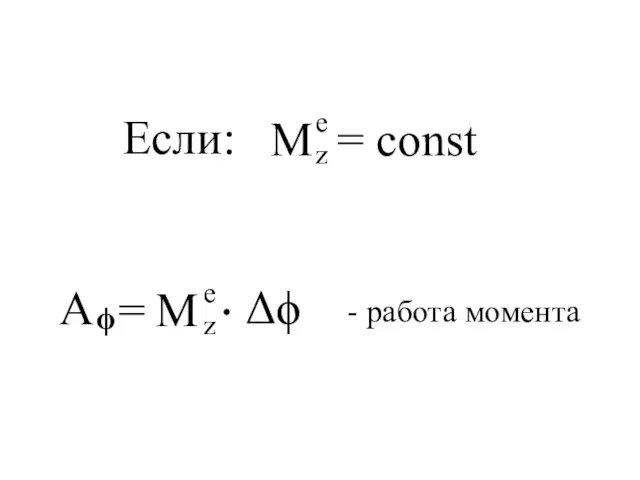











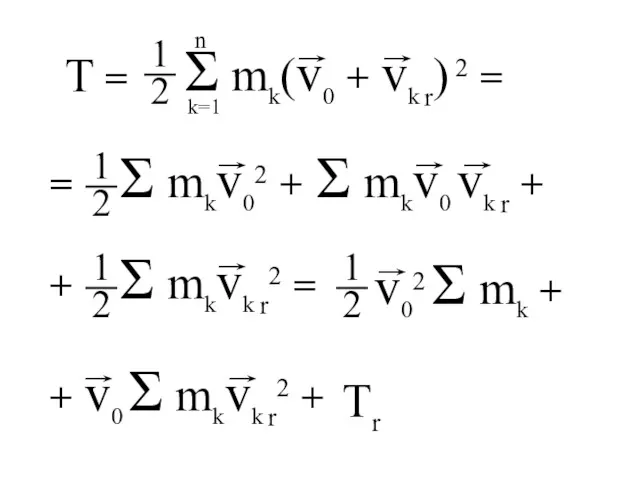








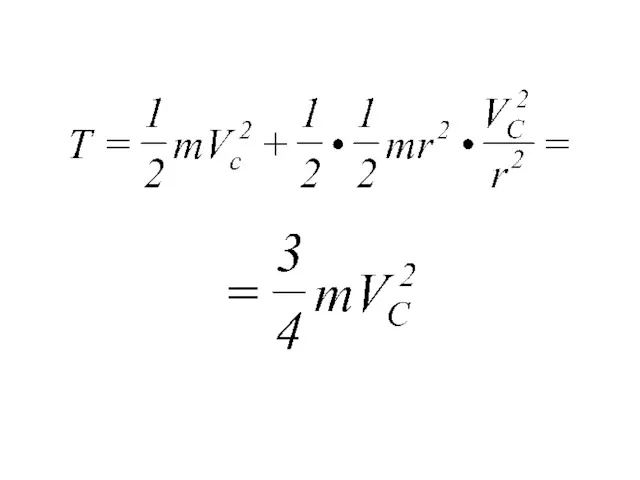


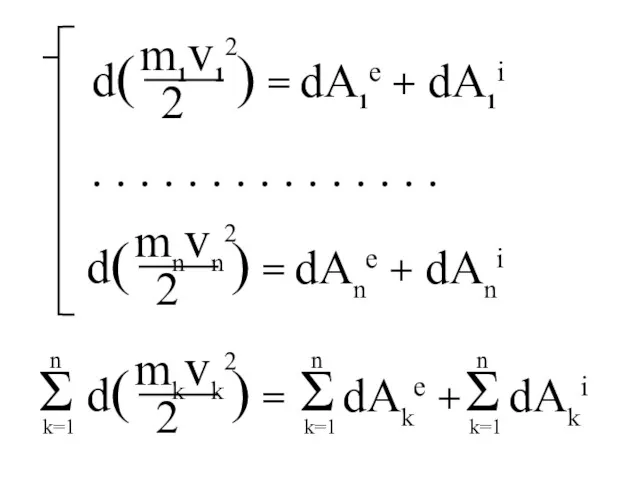










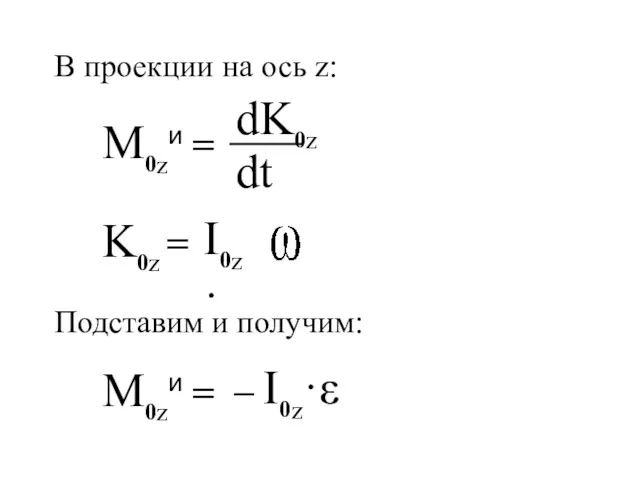





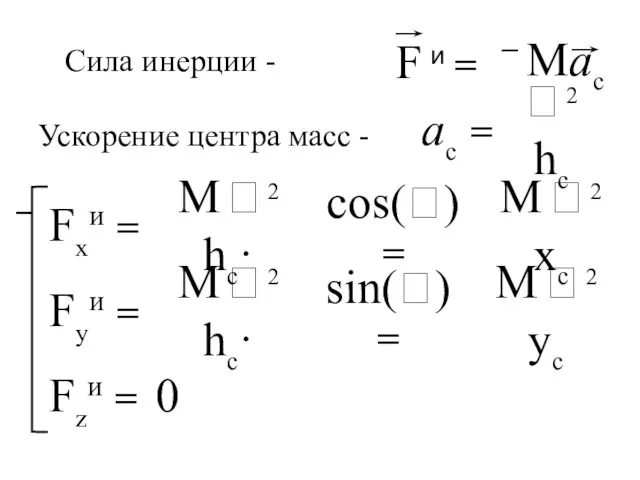

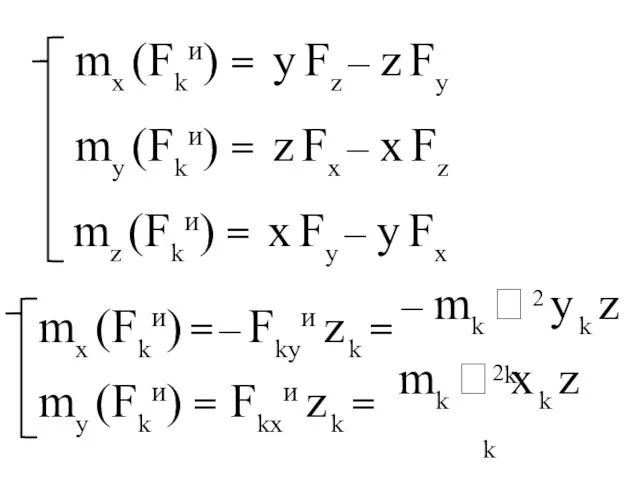













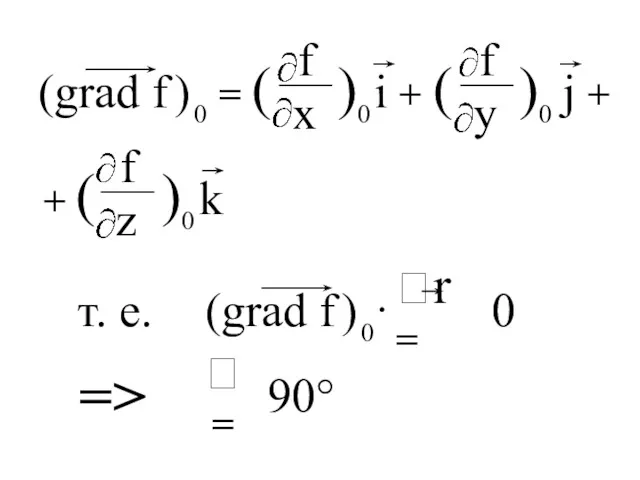




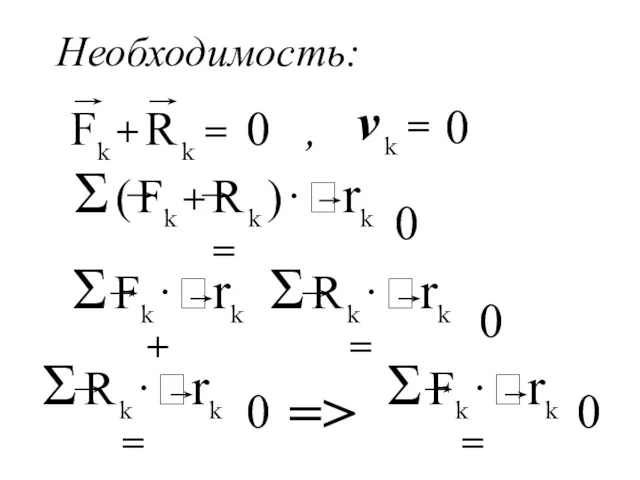
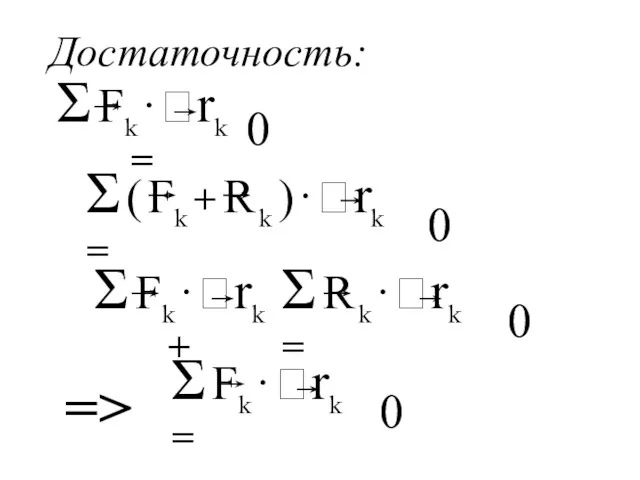

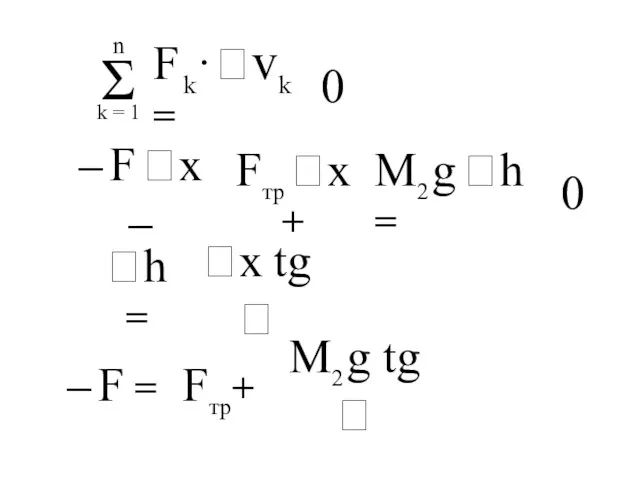
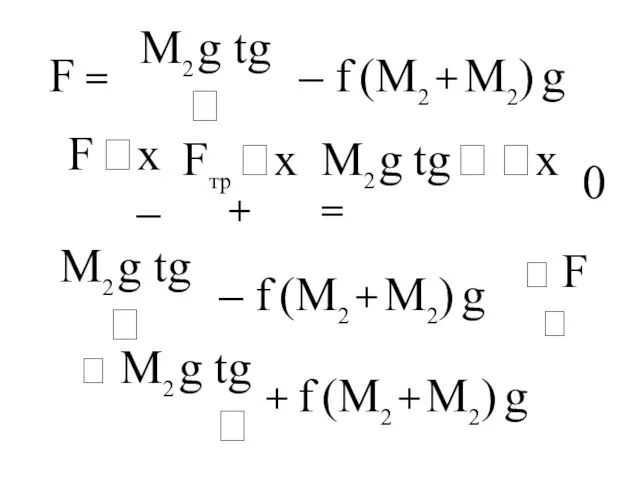







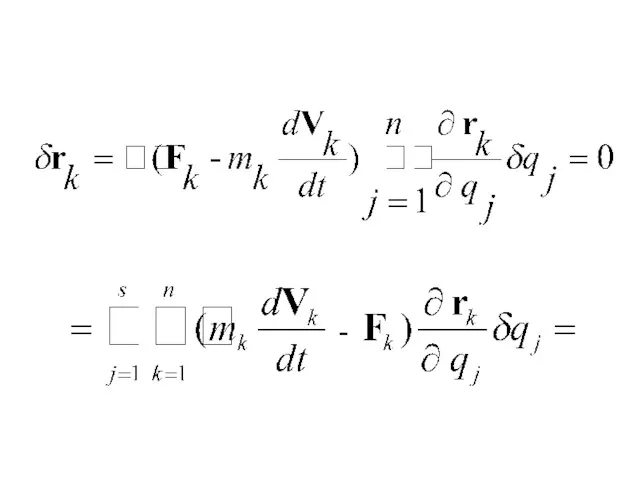
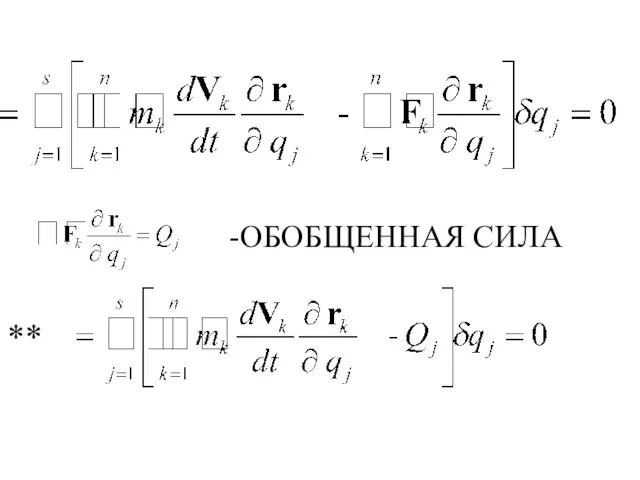

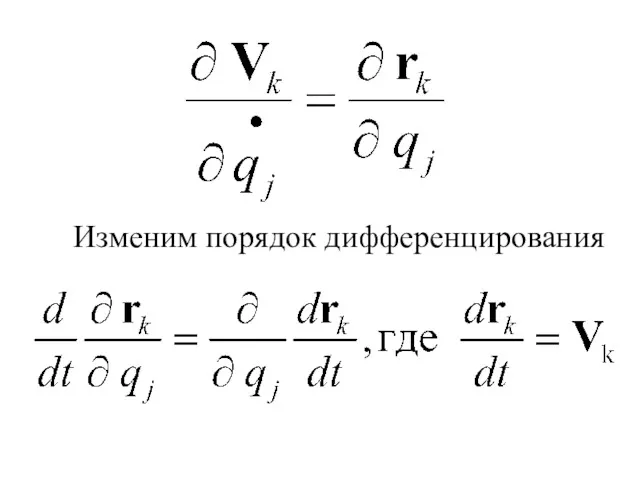
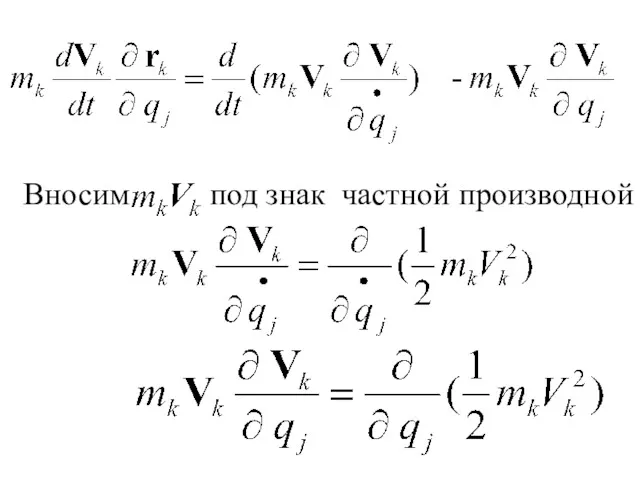
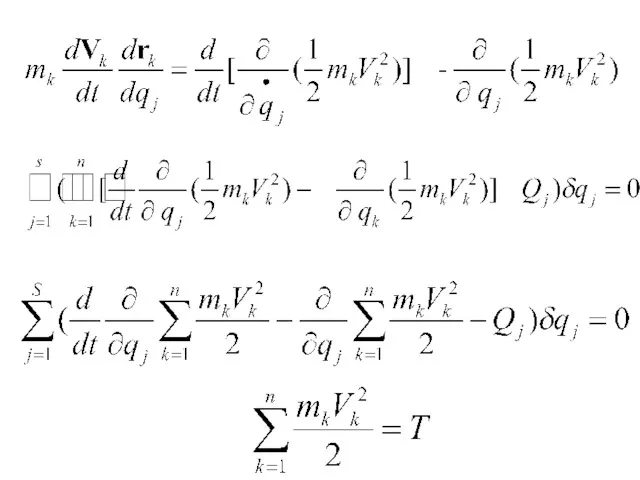
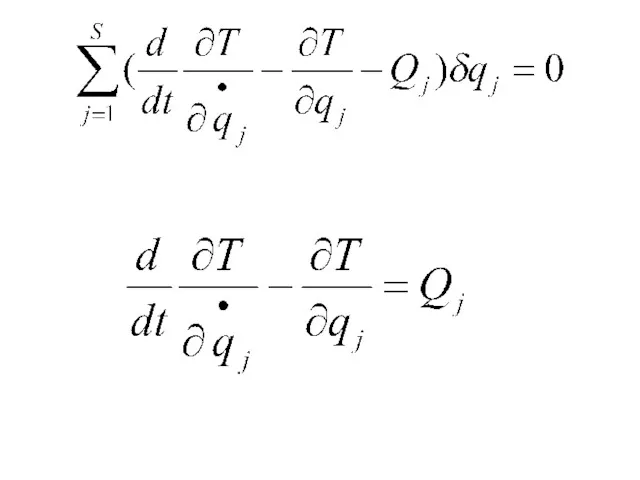



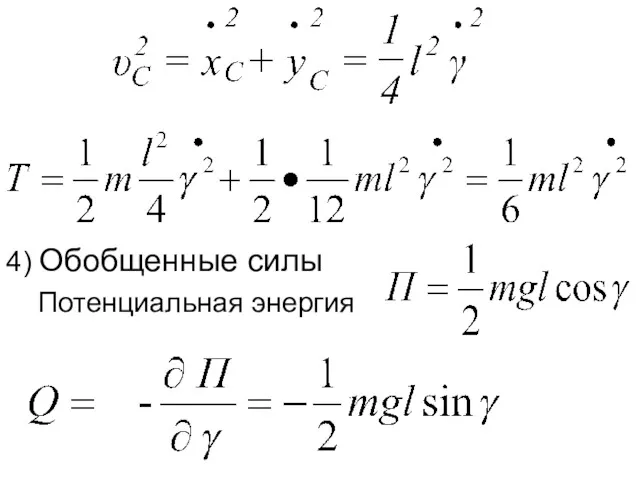
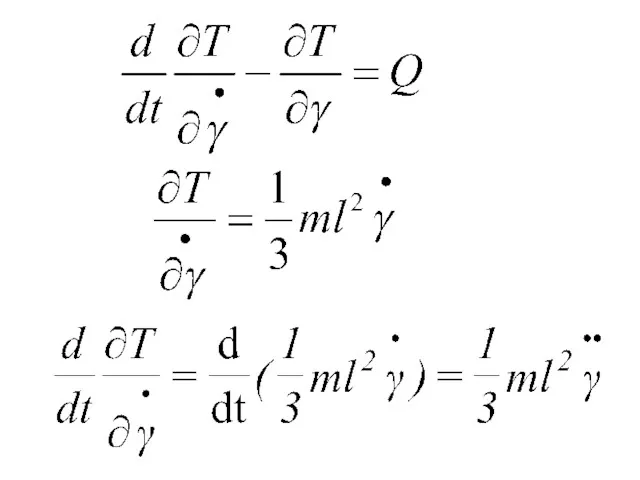

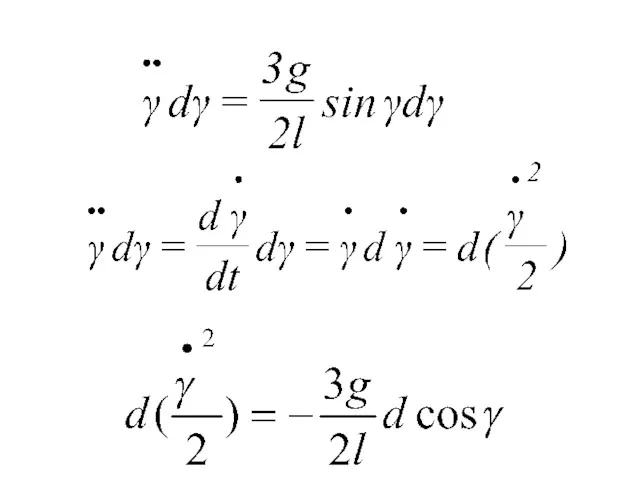
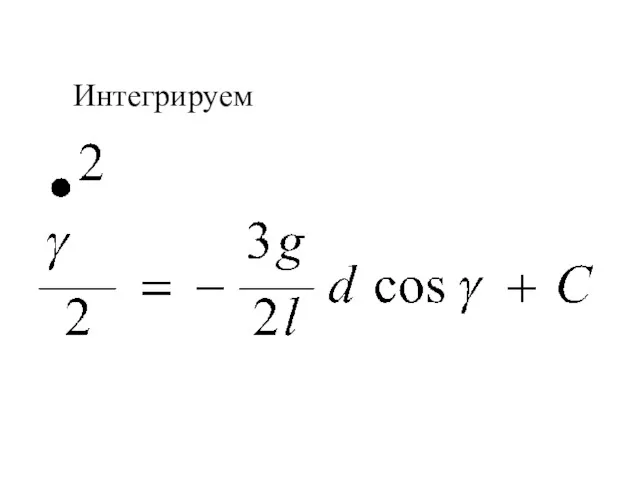
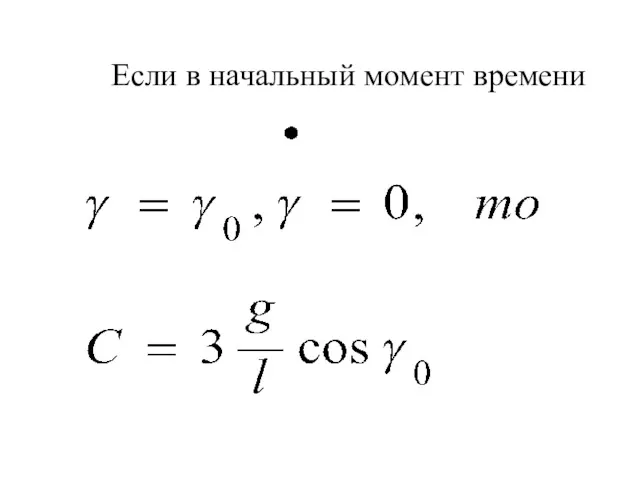
 Електромагнітні хвилі
Електромагнітні хвилі Основные понятия и законы динамики
Основные понятия и законы динамики Mechanical System
Mechanical System Архимедова сила. Подготовка к ГИА
Архимедова сила. Подготовка к ГИА Introduction & overview
Introduction & overview Формирование регулятивных универсальных учебных действий на уроках физики при проведении лабораторной работы
Формирование регулятивных универсальных учебных действий на уроках физики при проведении лабораторной работы Конструкції кип’ятильників і водонагрівальних пристроїв
Конструкції кип’ятильників і водонагрівальних пристроїв Использование полного внутреннего отражения
Использование полного внутреннего отражения Механика, оның бөлімдері және қозғалысты оқып үйренуде қолданылатын абстракциялық ұғымдар
Механика, оның бөлімдері және қозғалысты оқып үйренуде қолданылатын абстракциялық ұғымдар Вынужденные колебания
Вынужденные колебания Физические основы гемодинамики
Физические основы гемодинамики Изобретение электричества. История, применение, получение
Изобретение электричества. История, применение, получение 1949 – 1989 - 1991
1949 – 1989 - 1991 Энергия связи. Дефект масс
Энергия связи. Дефект масс Открытие нейтрона
Открытие нейтрона Электроспиннинг
Электроспиннинг Состояние электронов в атоме
Состояние электронов в атоме Механические свойства материалов. Диаграммы растяжения и сжатия. (Лекция 4)
Механические свойства материалов. Диаграммы растяжения и сжатия. (Лекция 4) Проявление сил тяжести и упругости живой природе
Проявление сил тяжести и упругости живой природе Від рівноважного випромінювання до лазера
Від рівноважного випромінювання до лазера Распиливание и припасовка
Распиливание и припасовка Исследовательский проект Машина Голдберга Разбивалка яйиц
Исследовательский проект Машина Голдберга Разбивалка яйиц презентация Обнаружение магнитного поля по его действию на электрический ток
презентация Обнаружение магнитного поля по его действию на электрический ток Определение перемещений в плоских стержневых конструкциях
Определение перемещений в плоских стержневых конструкциях Механика. Механическое движение
Механика. Механическое движение Кинематика точки
Кинематика точки Влияние наушников на слух человека
Влияние наушников на слух человека Обобщающий урок по теме Движение и взаимодействие тел
Обобщающий урок по теме Движение и взаимодействие тел