Содержание
- 2. Кузнецов Сергей Иванович доцент кафедры общей физики ТПУ Ф И З И К А Часть 2
- 3. Физика Кафедра общей физики Осенний семестр Лектор Кузнецов С.И. 2011/2012учебный год Гр. Лекции - 36 часoв
- 4. Литература 1. Ю.И. Тюрин, И.П. Чернов, Ю.Ю. Крючков ФИЗИКА, Ч.2. Электричество и магнетизм. 2. И.В. Савельев,
- 5. О курсе общей физики ЛИТЕРАТУРА
- 6. О курсе общей физики ЛИТЕРАТУРА
- 7. О курсе общей физики ЛИТЕРАТУРА
- 8. О курсе общей физики ЛИТЕРАТУРА
- 9. О курсе общей физики РЕЙТИНГ II семестр Посещение лекции – 5 баллов; 17 х 5 =
- 10. О курсе общей физики РЕЙТИНГ «отлично» - 951 балл и выше «хорошо» - 851 - 950
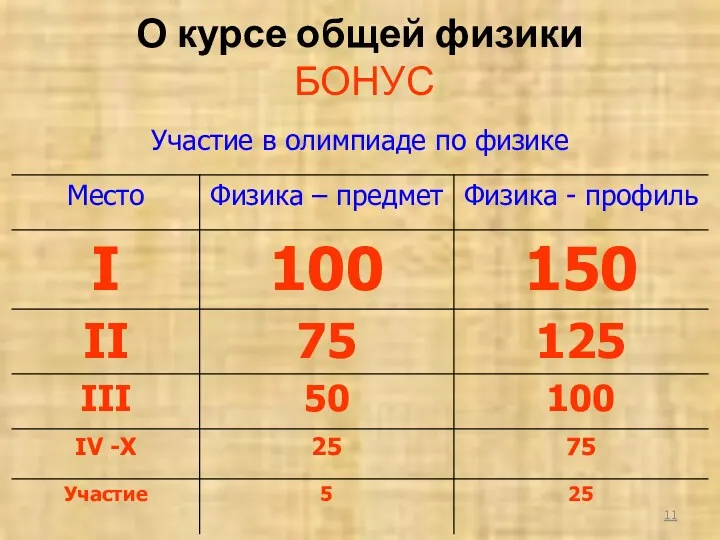
- 11. О курсе общей физики БОНУС
- 12. О курсе общей физики БОНУС 20 баллов за каждую задачу, если ИДЗ сдано за две недели
- 13. О курсе общей физики БОНУС 25 баллов за реферат, написанный студентом на предложенную им самим или
- 14. Тема 1. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ 1.1. Электрический заряд. Закон сохранения заряда 1.2. Взаимодействие электрических зарядов
- 15. Первыми известными человеку проявлениями "животного электричества" были разряды электрических рыб. Электрического сома изображали еще на древнеегипетских
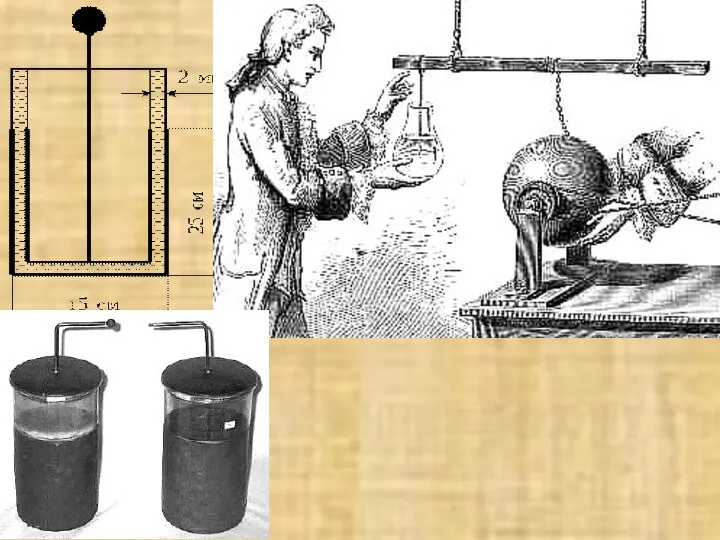
- 16. Важное место в истории науки об электричестве принадлежит немецкому бургомистру Герике, весившему триста фунтов. Он изобрел
- 17. Благодаря работам Грея (Англия, 1701-1770 гг.), опыты по передаче электричества на расстояние вышли за пределы помещения.
- 18. Для обнаружения малого заряда Грей пользовался длинным куском тонкой нити, подвешенным к концу палки. 31 мая
- 19. Лейденская банка была изобретена в 1745 г. независимо голландским профессором Питером Ван Мушенброком (1692-1761 гг.) и
- 20. «Зная, что стекло не проводит электричества, Мушенброк взял стеклянную банку (колбу), наполненную водой, опустил в нее
- 21. Изобретение лейденской банки ознаменовалось ее разрядом через тело экспериментатора. Вскоре стали проводить опыты с разрядом лейденской
- 23. Лейденская банка из Королевского шотландского музея в Эдинбурге
- 24. Электрические заряды не существуют сами по себе, а являются внутренними свойствами элементарных частиц – электронов, протонов
- 25. Закон сохранения заряда – один из фундаментальных законов природы, сформулированный в 1747 г. Б. Франклином и
- 26. 1868 г. - 1953 г. Самые красивые физические эксперименты в истории человечества: №9. Эксперимент американского физика,
- 27. Английский физик Уилсон попытался определить величину заряда электрона, исследуя влияние электрического поля на заряженное облако паров
- 28. К 1909 г. М. удалось определить, что заряд любой капельки всегда был целым кратным фундаментальной величине.
- 30. Частным случаем электродинамики является электростатика, представляющая собой учение о взаимодействии электрических зарядов. Основу электростатики составляют: -
- 31. 1.1. Электрический заряд Электростатика – раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля.
- 32. Сила взаимодействия между зарядами определяется только их взаимным расположением. Следовательно, энергия электростатического взаимодействия – потенциальная энергия.
- 33. Несмотря на обилие различных веществ в природе, существуют только два вида электрических зарядов: заряды подобные тем,
- 34. Франклин Бенджамин (1706 – 1790) американский физик, политический и общественный деятель. Основные работы в области электричества.
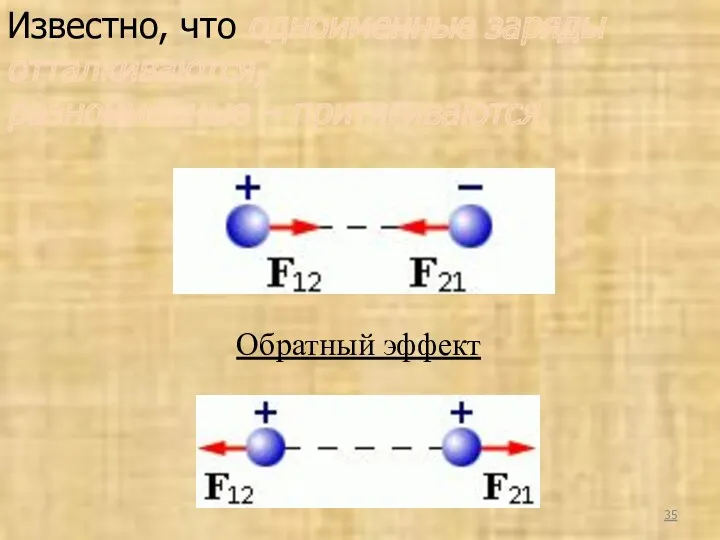
- 35. Обратный эффект Известно, что одноименные заряды отталкиваются, разноименные – притягиваются.
- 36. Если поднести заряженное тело (с любым зарядом) к легкому – незаряженному, то между ними будет притяжение
- 37. Таким образом, всякий процесс заряжения есть процесс разделения зарядов. Сумма зарядов не изменяется, заряды только перераспределяются.
- 38. Отсюда следует закон сохранения заряда – один из фундаментальных законов природы, сформулированный в 1747 г. Б.
- 39. Закон сохранения заряда суммарный электрический заряд замкнутой системы не изменяется.
- 40. Электрические заряды не существуют сами по себе, а являются внутренними свойствами элементарных частиц – электронов, протонов
- 41. Заряд q любого тела составляет целое кратное от элементарного электрического заряда : где n – целое
- 42. Электрон и протон являются соответственно носителями элементарных отрицательного и положительного зарядов.
- 43. Например, наша Земля имеет отрицательный заряд - 6 * 105Кл это установлено по измерению напряженности электростатического
- 44. Большой вклад в исследование явлений электростатики внес знаменитый французский ученый Ш. Кулон. В 1785 г. он
- 45. Кулон Шарль Огюстен (1736 – 1806) – французский физик и военный инженер. Работы относятся к электричеству,
- 46. 1.2. Взаимодействие электрических зарядов в вакууме. Точечным зарядом (q) называется заряженное тело, размеры которого пренебрежительно малы
- 47. Закон Кулона сила взаимодействия точечных зарядов в вакууме пропорциональна величине зарядов и обратно пропорциональна квадрату расстояния
- 48. здесь k0 – коэффициент пропорциональности, зависящий от системы единиц.
- 49. В системе СИ единица заряда 1 Кл = 1А * 1с где ε0 – электрическая постоянная;
- 50. Электрическая постоянная относится к числу фундаментальных физических констант и равна Элементарный заряд в СИ: Отсюда следует,
- 51. В векторной форме закон Кулона выглядит так: где F1 – сила, действующая на заряд q1 F2
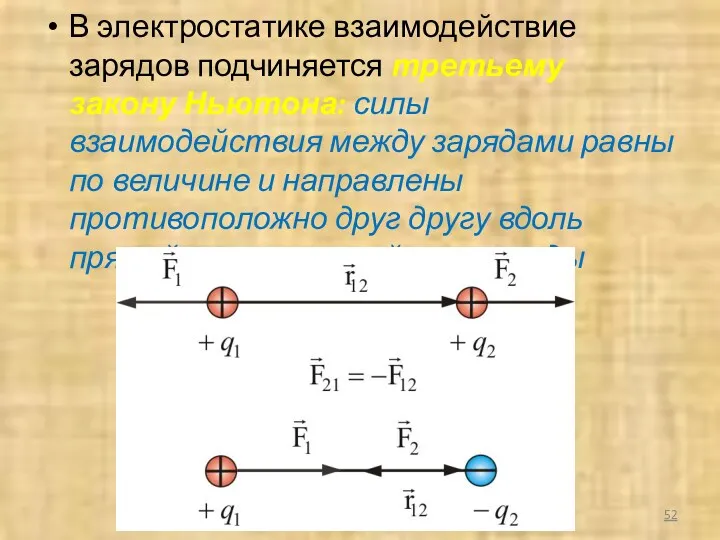
- 52. В электростатике взаимодействие зарядов подчиняется третьему закону Ньютона: силы взаимодействия между зарядами равны по величине и
- 53. Если заряды не точечные, то в такой форме закон Кулона не годится – нужно разбить заряженное
- 54. Закон Кулона в основных чертах подобен закону всемирного тяготения Ньютона, в соответствии с которым все тела
- 55. При всей внешней схожести формулировок этих законов между ними имеются серьезные различия. Качественное различие заключаются в
- 56. Однако более существенным обстоятельством является количественный аспект, а именно: сила электростатического отталкивания двух электронов превышает силу
- 57. Сила кулоновского притяжения между электроном и протоном в атоме водорода в 1039 раз больше их гравитационного
- 58. 1.3. Электростатическое поле в вакууме. Напряженность электростатического поля Почему заряды взаимодействуют? Имелет место борьба двух теорий:
- 59. Вокруг заряда всегда есть электрическое поле, основное свойство которого заключается в том, что на всякий другой
- 60. ЭМП – есть не абстракция, а объективная реальность – форма существования материи, обладающая определенными физическими свойствами,
- 61. Силовой характеристикой поля, создаваемого зарядом q является отношение силы, действующей на пробный заряд q’ , помещенный
- 62. Силовая характеристикой поля – напряженность электростатического поля: q’ - пробный заряд
- 63. Напряженность в векторной форме здесь r – расстояние от заряда до точки, где мы изучаем это
- 64. Вектор напряженности электростатического поля равен силе, действующей в данной точке на помещенный в нее пробный единичный
- 65. В СИ размерность напряженности:
- 66. 1.4. Сложение электростатических полей. Принцип суперпозиции Если поле создается несколькими точечными зарядами, то на пробный заряд
- 67. Результирующая сила определится выражением: – это принцип суперпозиции или независимости действия сил
- 68. т.к. то – результирующая напряженность поля в точке, где расположен пробный заряд, так же подчиняется принципу
- 69. Напряженность результирующего поля, системы точечных зарядов равна векторной сумме напряженностей полей, созданных в данной точке каждым
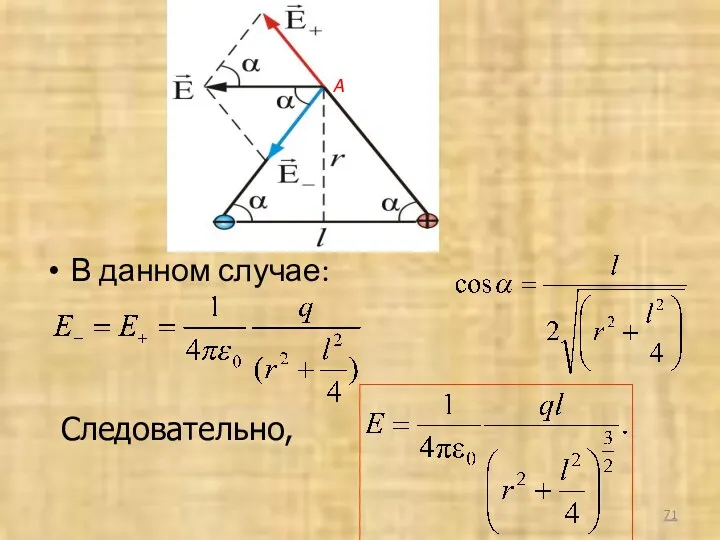
- 70. Пример 1 т. е. задача симметрична А
- 71. В данном случае: Следовательно, А
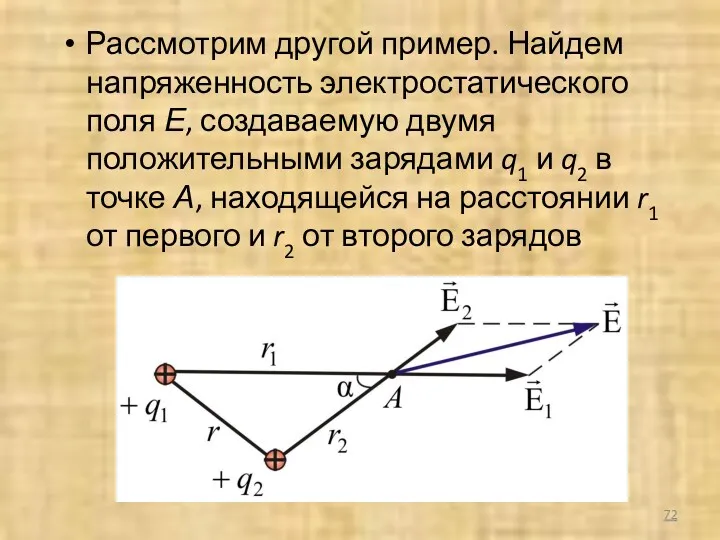
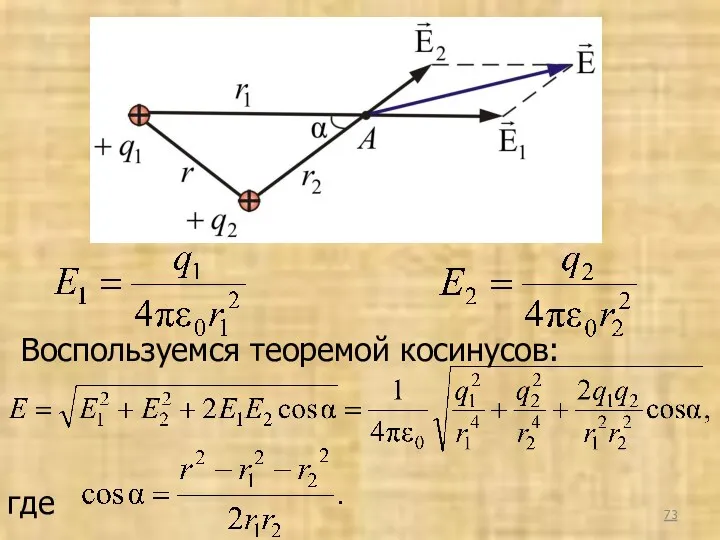
- 72. Рассмотрим другой пример. Найдем напряженность электростатического поля Е, создаваемую двумя положительными зарядами q1 и q2 в
- 73. Воспользуемся теоремой косинусов: где
- 74. Если поле создается не точечными зарядами, то используют обычный в таких случаях прием. Тело разбивают на
- 75. Для решения подобных задач пользуются соответствующими значениями плотности заряда: – линейная плотность заряда, измеряется в Кл/м;
- 76. Определим напряженность электрического поля в точке А на расстоянии х от бесконечно длинного, линейного, равномерно распределенного
- 77. Считаем, что х – мало по сравнению с длиной проводника. Элемент длины dy, несет заряд dq
- 78. Вектор имеет проекции dEx и dEy причем Т.к. проводник бесконечно длинный, а задача симметричная, то у
- 79. Тогда Теперь выразим y через θ. Т.к. То
- 80. Напряженность электрического поля линейно распределенных зарядов изменяется обратно пропорционально расстоянию до заряда.
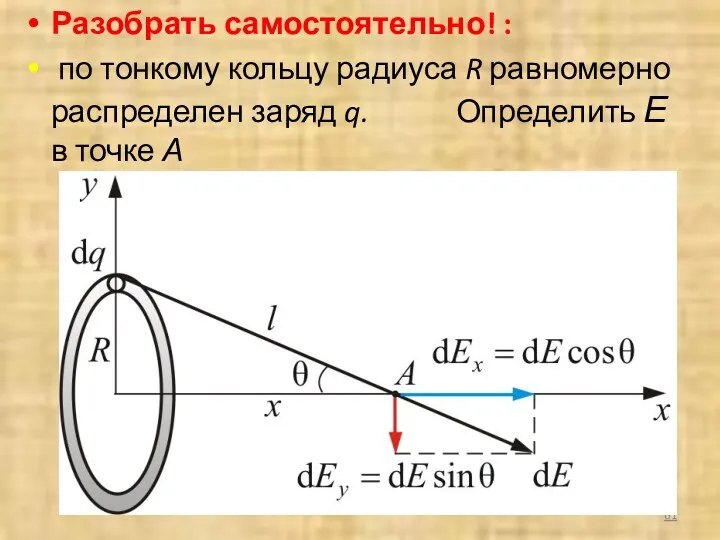
- 81. Разобрать самостоятельно! : по тонкому кольцу радиуса R равномерно распределен заряд q. Определить Е в точке
- 82. 1.5. Электростатическое поле диполя Электрическим диполем называется система двух одинаковых по величине, но разноименных точечных зарядов,
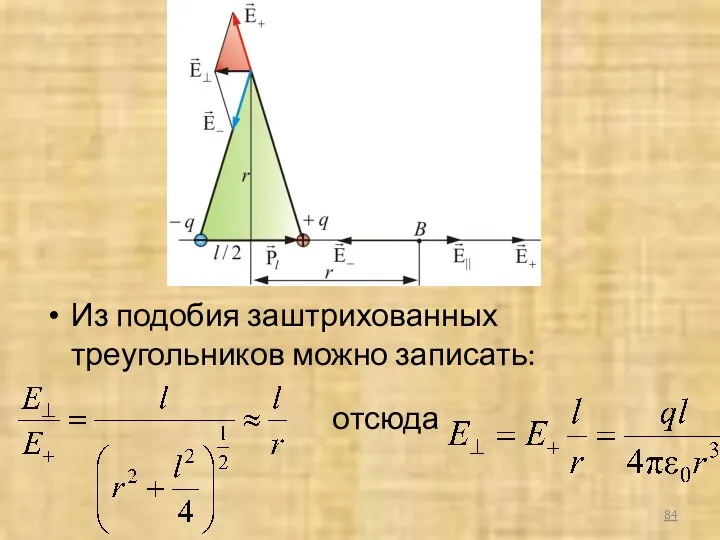
- 83. Пример 1. Найдем Е⊥ в точке А на прямой, проходящей через центр диполя и перпендикулярной к
- 84. Из подобия заштрихованных треугольников можно записать: отсюда
- 85. Обозначим вектор: – электрический момент диполя (или дипольный момент) – произведение положительного заряда диполя на плечо
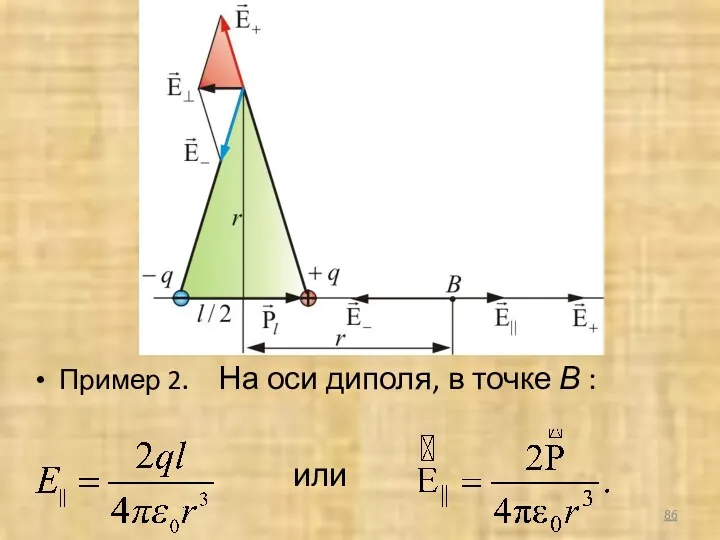
- 86. Пример 2. На оси диполя, в точке В : или
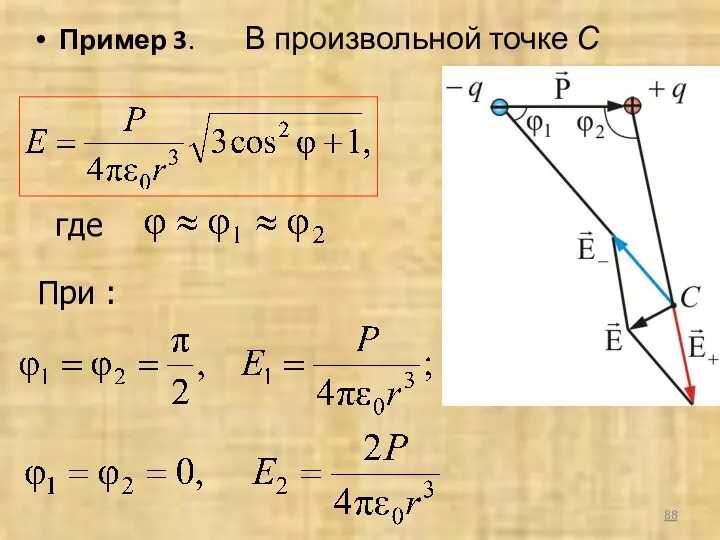
- 88. Пример 3. В произвольной точке С где При :
- 89. Электрическое поле диполя.
- 90. Из приведенных примеров видно, что напряженность электрического поля системы зарядов равна геометрической сумме напряженностей полей каждого
- 92. Скачать презентацию



























































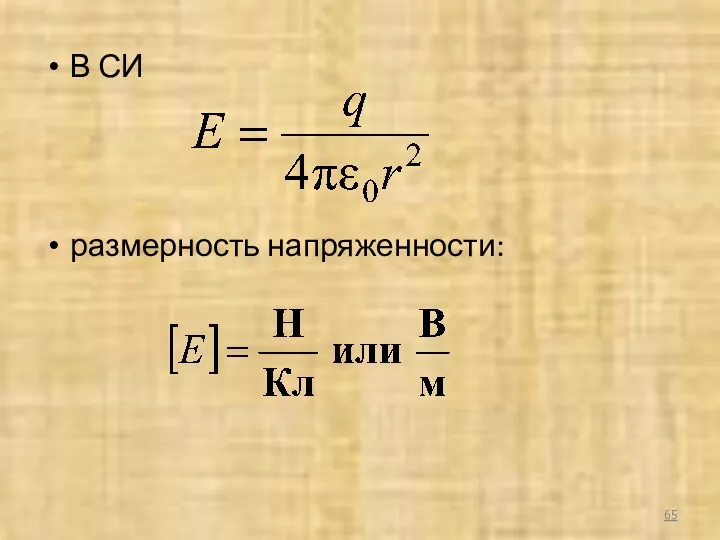


















 внеклассное мероприятие Как сберечь воду и уменьшить ее загрязнение для учащихся 6-7 классов
внеклассное мероприятие Как сберечь воду и уменьшить ее загрязнение для учащихся 6-7 классов Molecular-kinetic theory of ideal gases
Molecular-kinetic theory of ideal gases Динамика. Ньютон заңдары
Динамика. Ньютон заңдары Уравнения Максвелла. Вихревое электрическое поле
Уравнения Максвелла. Вихревое электрическое поле Радиотехническая отрасль, ее состав и значение для развития современного общества. Системы радиосвязи и радиовещания
Радиотехническая отрасль, ее состав и значение для развития современного общества. Системы радиосвязи и радиовещания Способы изменения внутренней энергии
Способы изменения внутренней энергии Передача информации с помощью электромагнитных волн
Передача информации с помощью электромагнитных волн Квантовые явления в оптике
Квантовые явления в оптике Взаимное притяжение и отталкивание между молекулами. Физика. 7 класс
Взаимное притяжение и отталкивание между молекулами. Физика. 7 класс Электромагнитные излучения небесных тел
Электромагнитные излучения небесных тел Ремонт раздаточной коробки LADA NIVA 4Х4 ВАЗ 2113. Правила и порядок заправки топливом ТС
Ремонт раздаточной коробки LADA NIVA 4Х4 ВАЗ 2113. Правила и порядок заправки топливом ТС План трассы. Вписывание круговых кривых с переходными кривыми
План трассы. Вписывание круговых кривых с переходными кривыми Закон Кулона. Напряженность поля точечного заряда
Закон Кулона. Напряженность поля точечного заряда Механічна робота. Потужність
Механічна робота. Потужність Проект “Дизельный двигатель”
Проект “Дизельный двигатель” Микроскоп – знакомство, создание, опыты
Микроскоп – знакомство, создание, опыты Электрический ток в полупроводниках
Электрический ток в полупроводниках Коллиматор. Разновидности коллиматоров. Виды тест-объектов. Зрительная труба. Диоптрийная трубка
Коллиматор. Разновидности коллиматоров. Виды тест-объектов. Зрительная труба. Диоптрийная трубка Потери мощности и энергии электроприводов
Потери мощности и энергии электроприводов Мастер-класс Подготовка к Единому государственному экзамену по Кинематике.
Мастер-класс Подготовка к Единому государственному экзамену по Кинематике. Ультрафиолетовые лучи
Ультрафиолетовые лучи Изнашивание неметаллических материалов
Изнашивание неметаллических материалов Закон всемирного тяготения. Сила тяжести. Невесомость
Закон всемирного тяготения. Сила тяжести. Невесомость Основные способы обработки деталей машин
Основные способы обработки деталей машин Принципы создания магнитных материалов. Магнитомягкие сплавы
Принципы создания магнитных материалов. Магнитомягкие сплавы Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение Молекулярная физика и термодинамика
Молекулярная физика и термодинамика Электрохимиялық талдау әдістері. Дәріс № 13-14
Электрохимиялық талдау әдістері. Дәріс № 13-14