Содержание
- 2. 02/06/2020 12:16 ص
- 3. Course Supplemental Materials Textbook - Engineering Mechanics: Dynamics, R. C. Hibbeler, 8th Edition, Pearson Prentice Hall,
- 4. Course Grading System 20% Attendance, participation, Quizzes and assignments 20% 1st Midterm Exam 20% 2nd Midterm
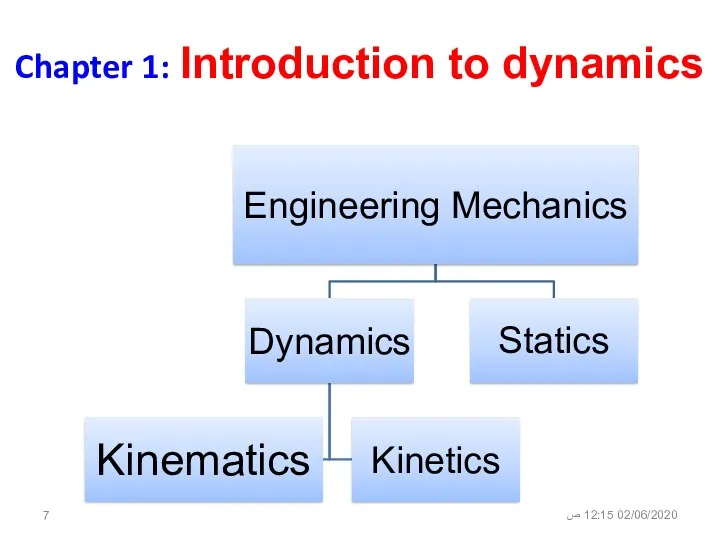
- 5. Course Topics Chapter 1: Introduction to dynamics Chapter 2: Kinematics of a Particle: Topic # 1:
- 6. Course Topics – Cont. Chapter 4: Planer Kinematics of a Rigid Body. Chapter 5: Planar Kinetics
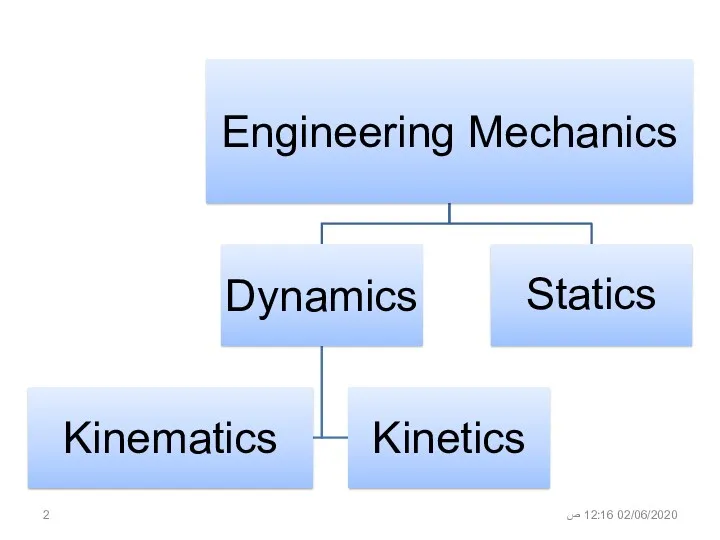
- 7. Chapter 1: Introduction to dynamics 02/06/2020 12:15 ص
- 8. Definitions 02/06/2020 12:15 ص Statics: concerned with the equilibrium of a body that is either at
- 9. Definitions – Cont. 02/06/2020 12:15 ص Dynamics 1- Kinematics: study of the motion of particles/rigid bodies
- 10. Definitions – Cont. Rigid Body Particle 02/06/2020 12:15 ص
- 11. Review of Vectors and Scalars A Scalar quantity has magnitude only. A Vector quantity has both
- 12. Scalars (e.g) Distance Mass Temperature Pure numbers Time Pressure Area Volume Vectors (e.g.) Displacement Velocity Acceleration
- 13. Vectors Can be represented by an arrow (called the “vector”). Length of a vector represents its
- 14. Chapter 2: Kinematics of a Particle: Topic # 1: Particle motion along a straight line (Rectilinear
- 15. Definition Rectilinear motion: A particle moving along a horizontal/vertical/inclined straight line.
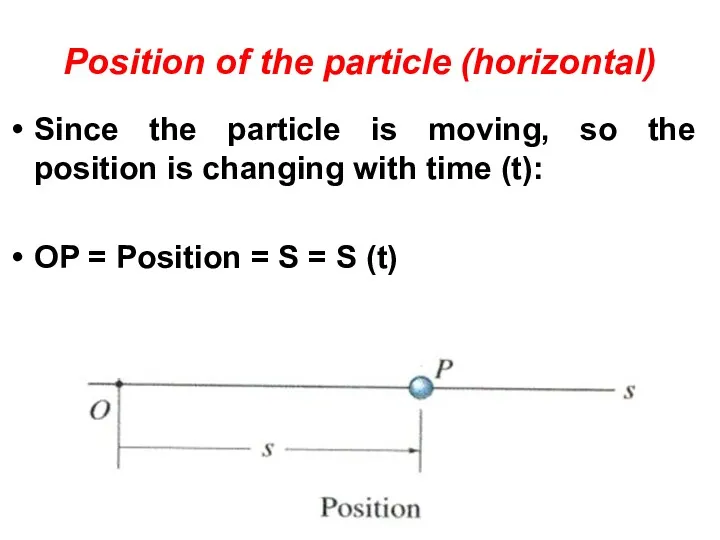
- 16. Position of the particle (horizontal) Since the particle is moving, so the position is changing with
- 17. Displacement of the particle (horizontal) Displacement (∆s) : The displacement of the particle is the change
- 18. Displacement of the particle (horizontal) 1- ∆S is positive since the particle's final position is to
- 19. Velocity of the particle (horizontal) Velocity (v) : If the particle displacement ∆s during time interval
- 20. Instantaneous velocity : Velocity of the particle (horizontal) So (v) is a function of time (t):
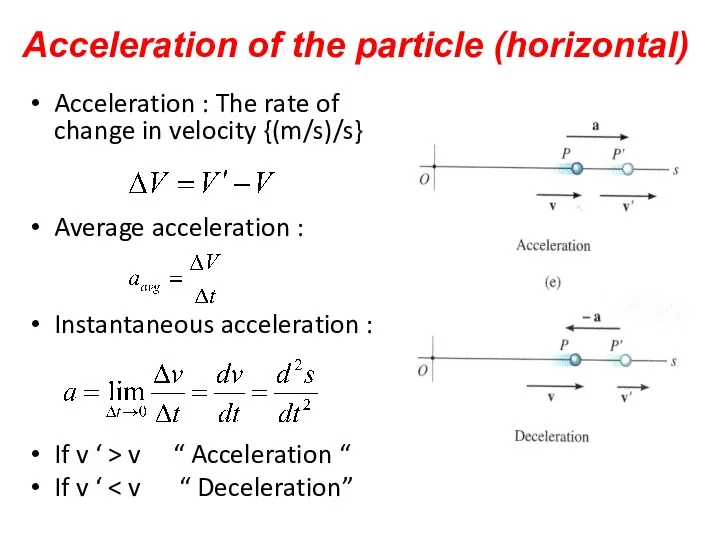
- 21. Acceleration : The rate of change in velocity {(m/s)/s} Average acceleration : Instantaneous acceleration : If
- 22. Acceleration of the particle (horizontal) Acceleration (a) : is the rate of change of velocity with
- 23. Solved Examples A particle moves along a straight line such that its position is defined by
- 24. A particle moves along a straight line such that its position is defined by s =
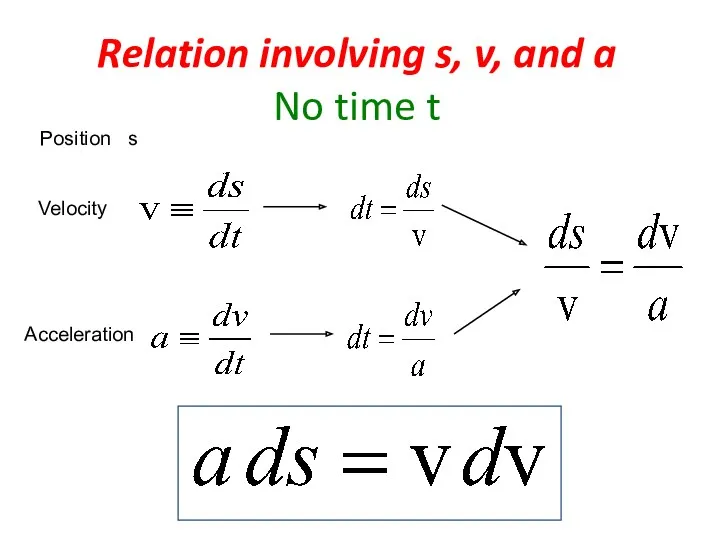
- 25. Relation involving s, v, and a No time t Position s
- 26. Motion with uniform/constant acceleration a
- 27. Motion with uniform/constant acceleration a
- 28. Motion with uniform/constant acceleration a
- 29. Summary Time dependent acceleration Constant acceleration
- 30. A car moves in a straight line such that for a short time its velocity is
- 31. Chapter 2: Kinematics of a Particle: Topic # 2: Particle Motion along a Curved Path
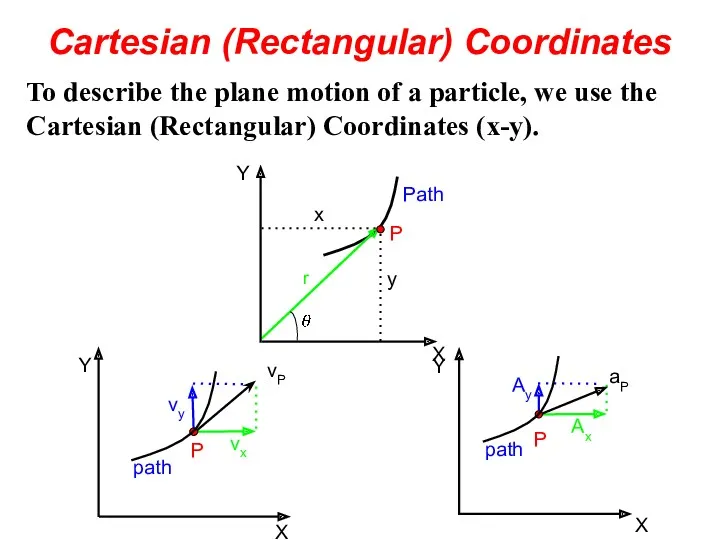
- 32. Cartesian (Rectangular) Coordinates To describe the plane motion of a particle, we use the Cartesian (Rectangular)
- 33. 12Projectile Motion Projectile: any body that is given an initial velocity and then follows a path
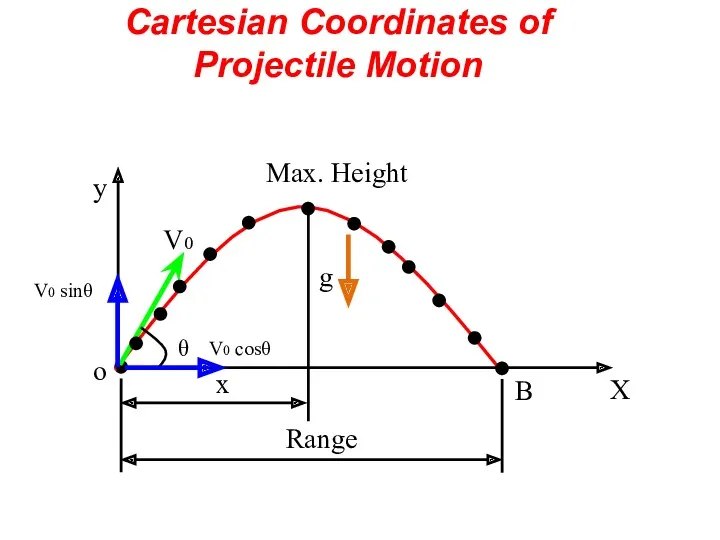
- 34. Max. Height Cartesian Coordinates of Projectile Motion B
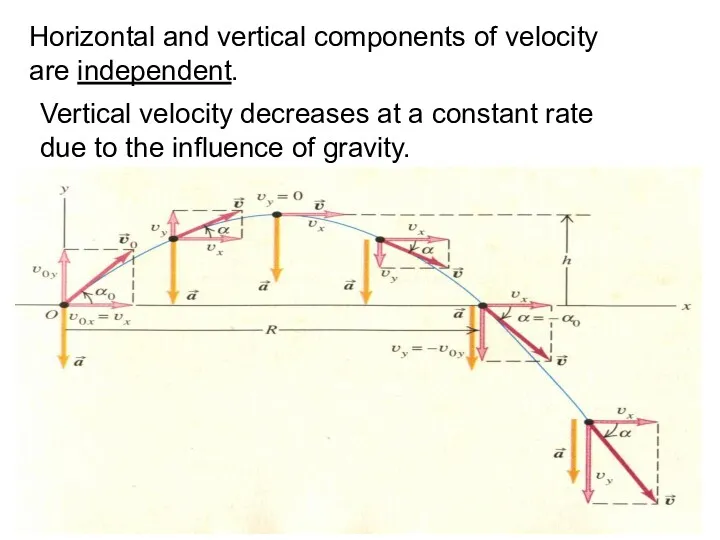
- 35. Horizontal and vertical components of velocity are independent. Vertical velocity decreases at a constant rate due
- 36. Cartesian Coordinates of Projectile Motion Assumptions: (1) free-fall acceleration (2) neglect air resistance Choosing the y
- 37. Horizontal Motion of Projectile Acceleration in X-direction: ax= 0 Integrate the acceleration yields: Integrate the velocity
- 38. Vertical Motion of Projectile ay = ac= -g = -9.81 m/s2 Integrate the acceleration yields: Integrate
- 39. ax = 0; ay = - g (a constant) Integration of these acceleration yields Elimination of
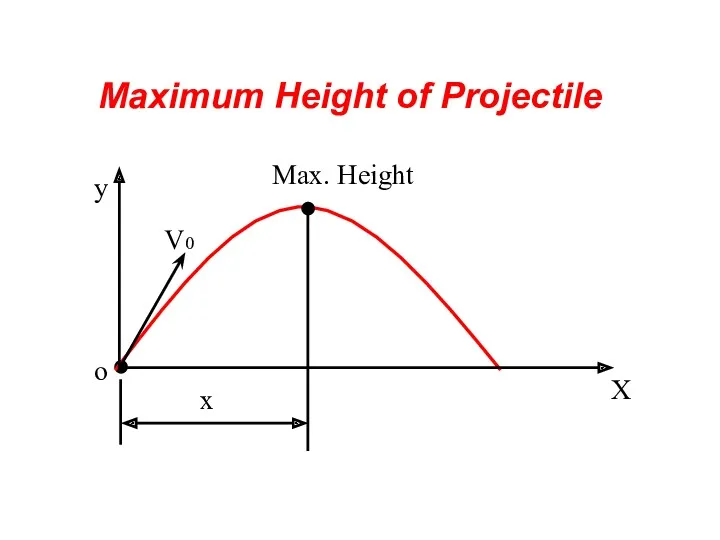
- 40. Max. Height Maximum Height of Projectile
- 41. Maximum Height of Projectile At the peak of its trajectory, vy = 0. Time t1 to
- 42. Maximum Height of Projectile
- 43. Maximum Height of Projectile and the corresponding time and X
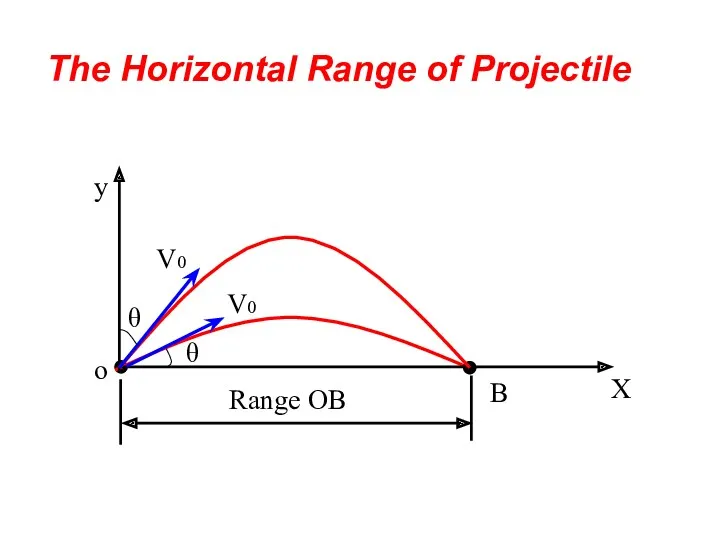
- 44. B The Horizontal Range of Projectile
- 45. The Horizontal Range of Projectile The range (OB) where y = 0. Time for the range
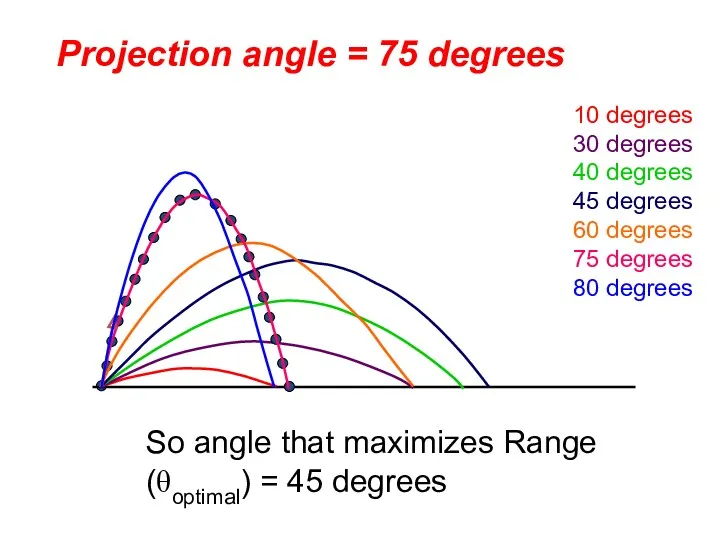
- 46. The Horizontal Range of Projectile From the Rang equation it is clear that an angle of
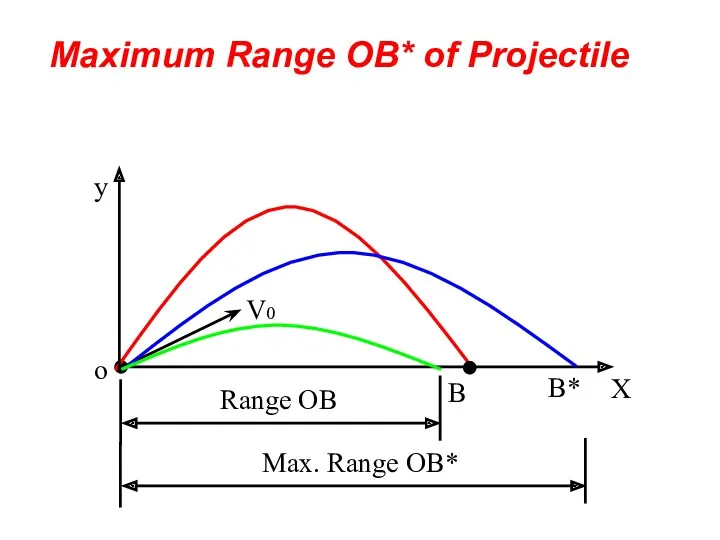
- 47. B Maximum Range OB* of Projectile B*
- 48. Maximum Range OB* of Projectile To calculate max. Range (OB*) and its angle
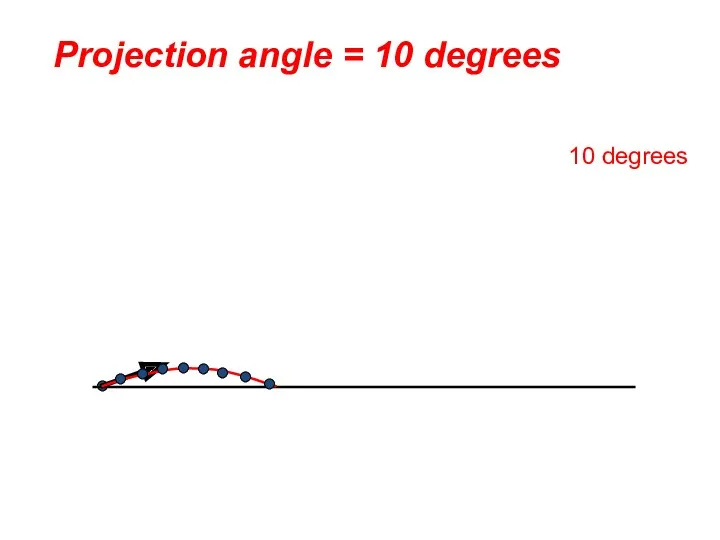
- 49. Projection Angle The optimal angle of projection is dependent on the goal of the activity. For
- 50. 10 degrees Projection angle = 10 degrees
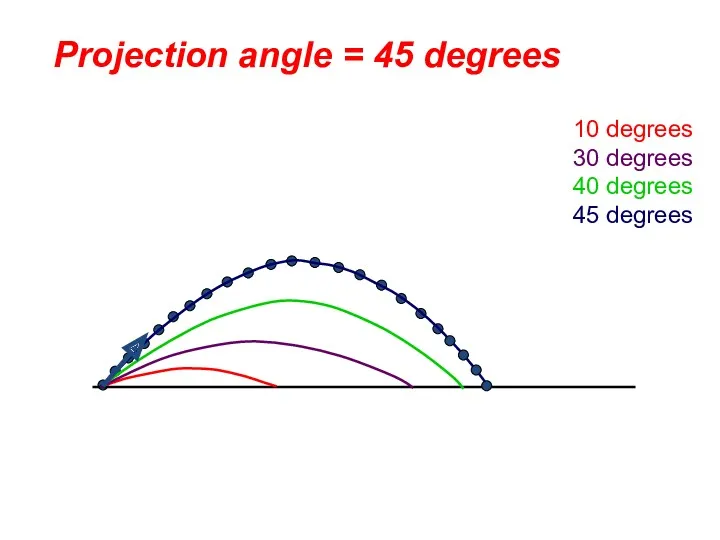
- 51. 10 degrees 30 degrees 40 degrees 45 degrees Projection angle = 45 degrees
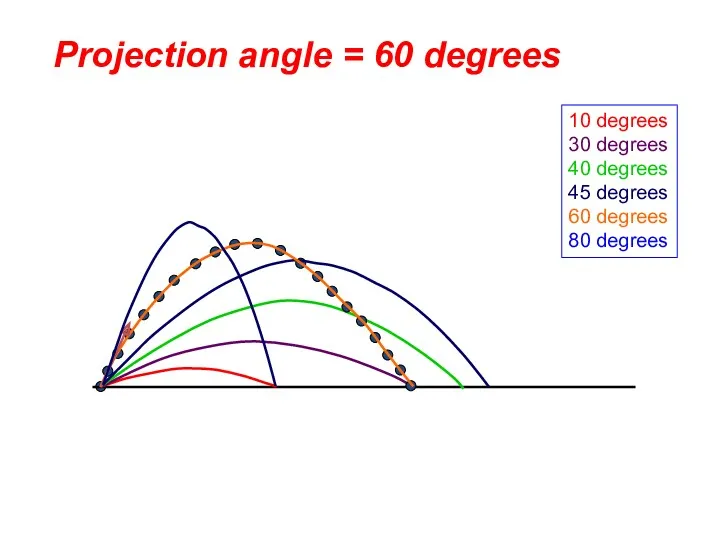
- 52. 10 degrees 30 degrees 40 degrees 45 degrees 60 degrees 80 degrees Projection angle = 60
- 53. 10 degrees 30 degrees 40 degrees 45 degrees 60 degrees 75 degrees 80 degrees Projection angle
- 55. Скачать презентацию





































 Газораспределительный механизм двигателя
Газораспределительный механизм двигателя Автоматическая система капельного полива огорода с помощью солнечного нагрева воды
Автоматическая система капельного полива огорода с помощью солнечного нагрева воды Электромагнитные устройства и трансформаторы
Электромагнитные устройства и трансформаторы Модели атома. Опыт Резерфорда
Модели атома. Опыт Резерфорда Работа и мощность электрического тока
Работа и мощность электрического тока Леонардо да Винчи
Леонардо да Винчи Ручная таль
Ручная таль Статические свойства атомных ядер. Ядерные модели
Статические свойства атомных ядер. Ядерные модели Источники света. Прямолинейное распространение света.
Источники света. Прямолинейное распространение света.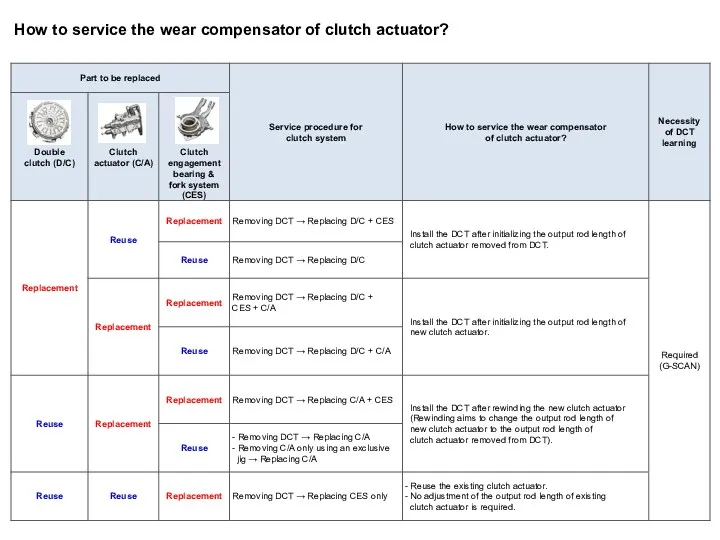 How to service the wear compensator of clutch actuator
How to service the wear compensator of clutch actuator Упругое рассеяние в центральном поле
Упругое рассеяние в центральном поле презентации к урокам
презентации к урокам Кручение стержней круглого сечения
Кручение стержней круглого сечения Inductance. Self-inductance
Inductance. Self-inductance Основы технической механики. Основы статики. Урок 1
Основы технической механики. Основы статики. Урок 1 Иллюзия или обман зрения
Иллюзия или обман зрения Астродинамика. Движение космических аппаратов по орбите
Астродинамика. Движение космических аппаратов по орбите Устройство кривошипно - шатунного механизма
Устройство кривошипно - шатунного механизма Фізичні та хімічні властивості води
Фізичні та хімічні властивості води Перспективные материалы и технологии. Экскурсия в наномир
Перспективные материалы и технологии. Экскурсия в наномир Как человек научился считать время (окружающий мир, 4 класс)
Как человек научился считать время (окружающий мир, 4 класс) Презентация Механическое движение
Презентация Механическое движение Цвет. Оптика
Цвет. Оптика Урок - исследование. Воздух и его свойства. Воздушная оболочка Земли
Урок - исследование. Воздух и его свойства. Воздушная оболочка Земли Рупорные антенны. (Лекция 12)
Рупорные антенны. (Лекция 12) Улаштування та ТО карбюраторів. ТО системи живлення карбюраторних двигунів
Улаштування та ТО карбюраторів. ТО системи живлення карбюраторних двигунів Атомные электростанции
Атомные электростанции тест Диск
тест Диск