Содержание
- 2. Общая характеристика теории Максвелла Основу теории Максвелла составляют четыре структурных уравнения, которые записываются в интегральной и
- 3. Теоремы векторного анализа Теорема Остроградского-Гаусса: поток Фа вектора а сквозь произвольную замкнутую поверхность S равен объемному
- 4. Теоремы векторного анализа Теорема Стокса: циркуляция вектора а вдоль замкнутого контура L равна поверхностному интегралу от
- 5. Первое уравнение Максвелла в интегральной и дифференциальной формах по сути, это закон электромагнитной индукции Фарадея с
- 6. Ток смещения Максвелл предположил, что источником МП может быть не только макроток (ток проводимости), но и
- 7. Второе уравнение Максвелла в интегральной и дифференциальной формах С учетом тока смещения закон полного тока для
- 8. Третье и четвертое уравнение Максвелла в интегральной и дифференциальной формах Максвелл обобщил теорему Остроградского-Гаусса для электростатического
- 9. Полная система структурных уравнений Максвелла для ЭМП в общем случае
- 10. Материальные уравнения и граничные условия для ЭМП Данные четыре структурных уравнения (табл. 1) дополняются тремя материальными
- 11. Полная система структурных уравнений Максвелла для стационарных ЭП и МП при наличии зарядов и токов проводимости
- 12. Полная система уравнений Максвелла состоит из Четырех структурных уравнений в интегральной или дифференциальной форме Трех материальных
- 14. Скачать презентацию











 Електрика: промислова, статична і атмосферна
Електрика: промислова, статична і атмосферна Ремонт автомобилей. Техническое нормирование ремонтных (ручных) работ. (Тема 5.3)
Ремонт автомобилей. Техническое нормирование ремонтных (ручных) работ. (Тема 5.3) Сила. Явление тяготения. Сила тяжести. Что такое сила?
Сила. Явление тяготения. Сила тяжести. Что такое сила?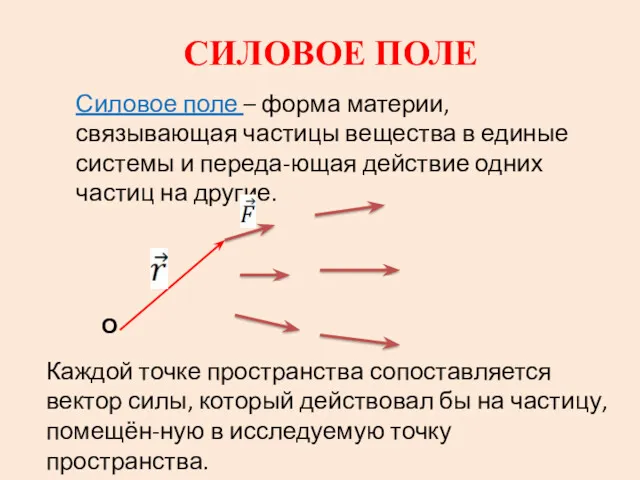 Силовое поле
Силовое поле Презентация Гелиоцентрическая система мира
Презентация Гелиоцентрическая система мира Механічні та електромагнітні хвилі
Механічні та електромагнітні хвилі Теориялық механика
Теориялық механика Аккумуляторы для крупномасштабного хранения энергии. Лекция 8
Аккумуляторы для крупномасштабного хранения энергии. Лекция 8 Тепловые двигатели и охрана окружающей среды
Тепловые двигатели и охрана окружающей среды Контактные явления. Контакт металл - полупроводник
Контактные явления. Контакт металл - полупроводник Влажность воздуха.
Влажность воздуха. Динамика материальной точки
Динамика материальной точки Тема урока: Влажность воздуха
Тема урока: Влажность воздуха Изменение агрегатных состояний вещества
Изменение агрегатных состояний вещества Изобретение радио. Принцип радиосвязи.
Изобретение радио. Принцип радиосвязи. решение задач на давление в жидкости
решение задач на давление в жидкости Причіпні пожежні мотопомпи. Експлуатація мотопомп
Причіпні пожежні мотопомпи. Експлуатація мотопомп Магнітне поле. Сила Ампера
Магнітне поле. Сила Ампера Работа и мощность электрического тока. 8 класс
Работа и мощность электрического тока. 8 класс През.ЮА.МС11-21
През.ЮА.МС11-21 Электрические цепи переменного тока. Лекция 2
Электрические цепи переменного тока. Лекция 2 Анимации на уроках физики.
Анимации на уроках физики. Lubrication
Lubrication Простые механизмы
Простые механизмы Урок-соревнование по физике в VIII классе по теме Тепловые явления +презентация
Урок-соревнование по физике в VIII классе по теме Тепловые явления +презентация Різновиди механізмів натиску листових друкарських машин
Різновиди механізмів натиску листових друкарських машин Моделирование процессов термомодифицирования древесины
Моделирование процессов термомодифицирования древесины Сборочные чертежи. Виды соединений деталей
Сборочные чертежи. Виды соединений деталей