Содержание
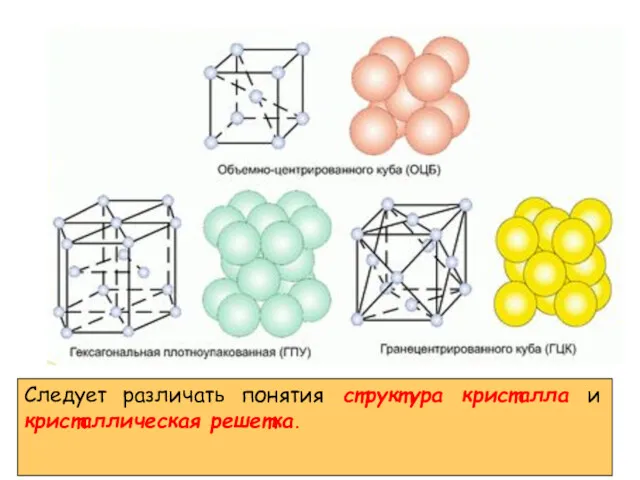
- 2. Следует различать понятия структура кристалла и кристаллическая решетка.
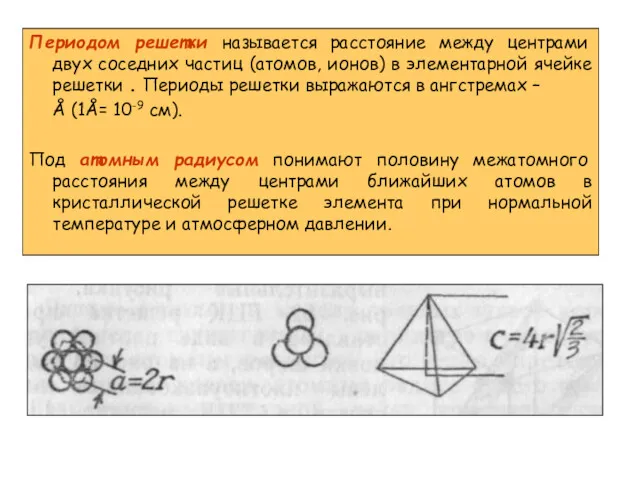
- 3. Периодом решетки называется расстояние между центрами двух соседних частиц (атомов, ионов) в элементарной ячейке решетки .
- 4. Энергия кристаллической решетки определяется как энергия, выделяющаяся при образовании кристалла из ионов, атомов или других частиц,
- 5. любую кристаллографическую плоскость и любую грань кристалла можно определить тремя целыми числами - индексами Миллера, которые
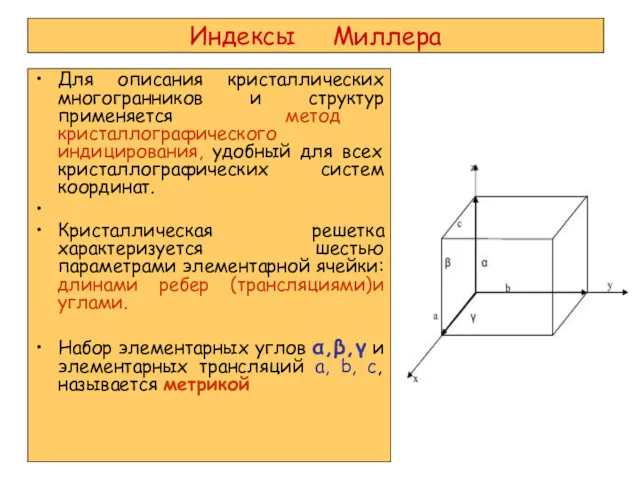
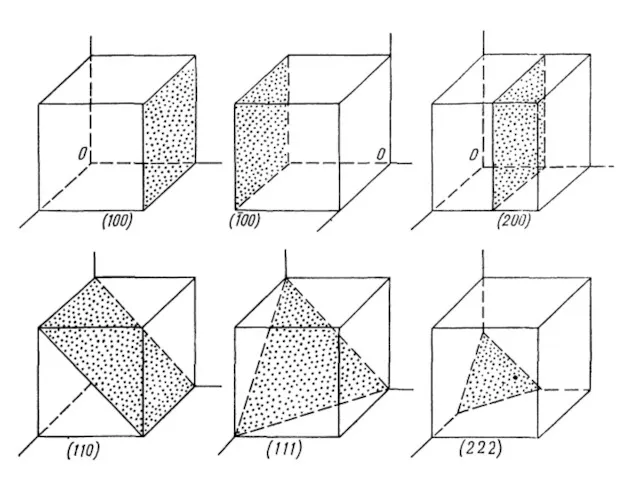
- 6. Индексы Миллера Для описания кристаллических многогранников и структур применяется метод кристаллографического индицирования, удобный для всех кристаллографических
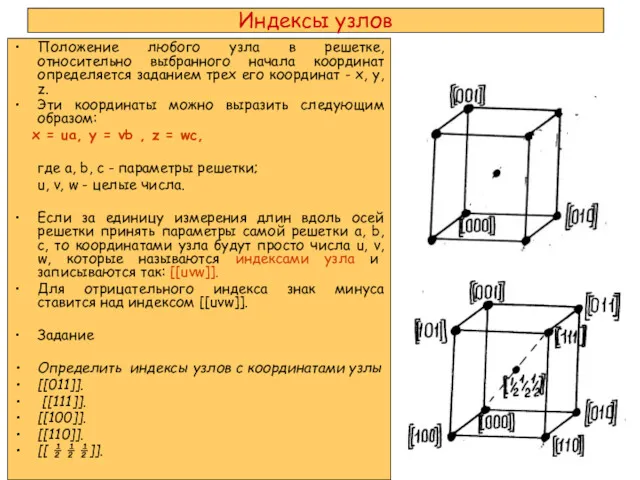
- 7. Индексы узлов Положение любого узла в решетке, относительно выбранного начала координат определяется заданием трех его координат
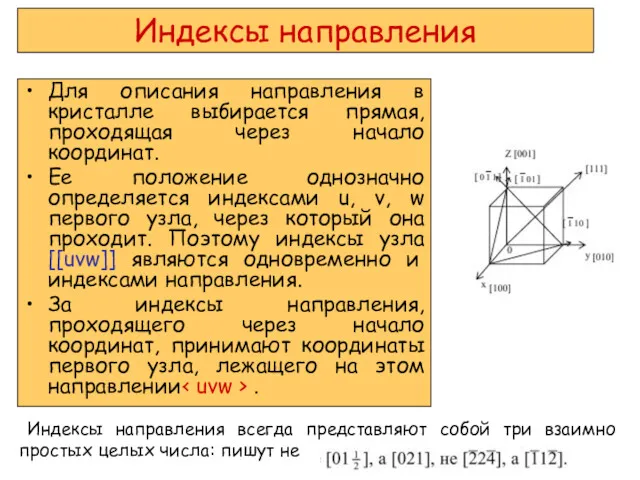
- 8. Индексы направления Для описания направления в кристалле выбирается прямая, проходящая через начало координат. Ее положение однозначно
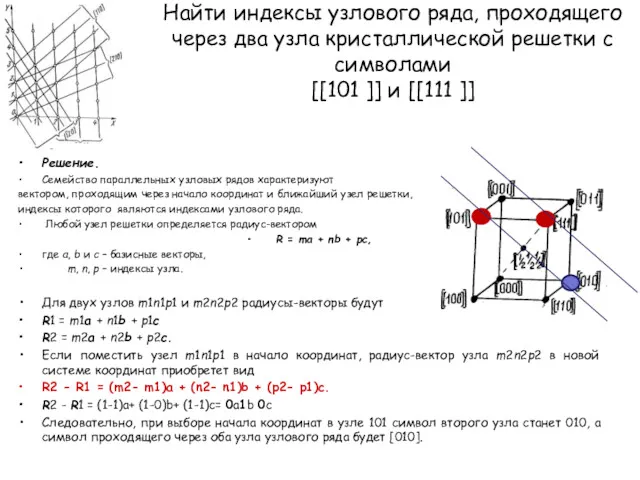
- 9. Найти индексы узлового ряда, проходящего через два узла кристаллической решетки с символами [[101 ]] и [[111
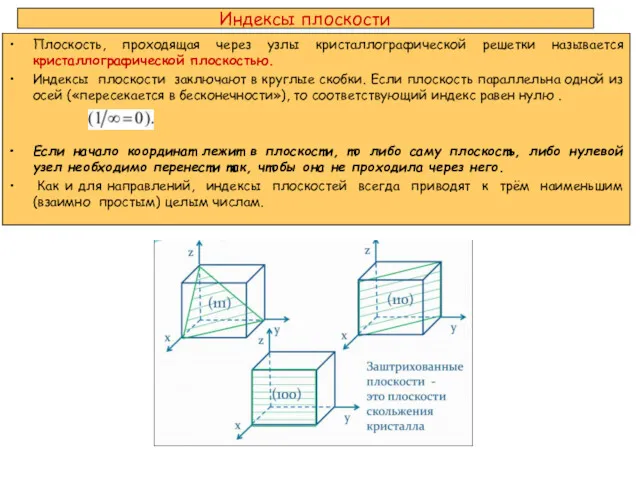
- 10. Плоскость, проходящая через узлы кристаллографической решетки называется кристаллографической плоскостью. Индексы плоскости заключают в круглые скобки. Если
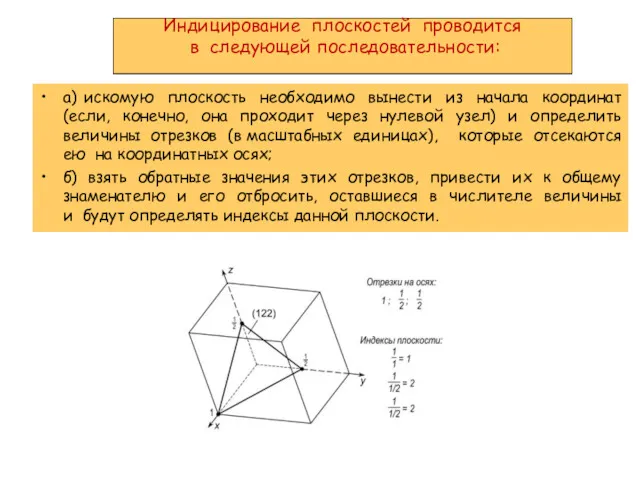
- 11. Индицирование плоскостей проводится в следующей последовательности: а) искомую плоскость необходимо вынести из начала координат (если, конечно,
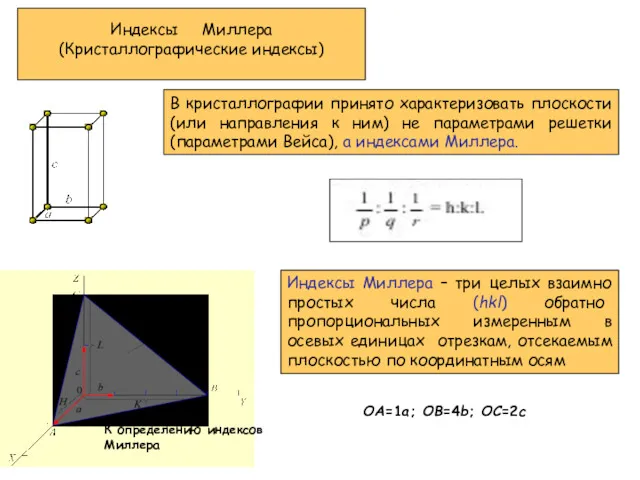
- 13. Индексы Миллера (Кристаллографические индексы) К определению индексов Миллера ОА=1а; ОВ=4b; OC=2c В кристаллографии принято характеризовать плоскости
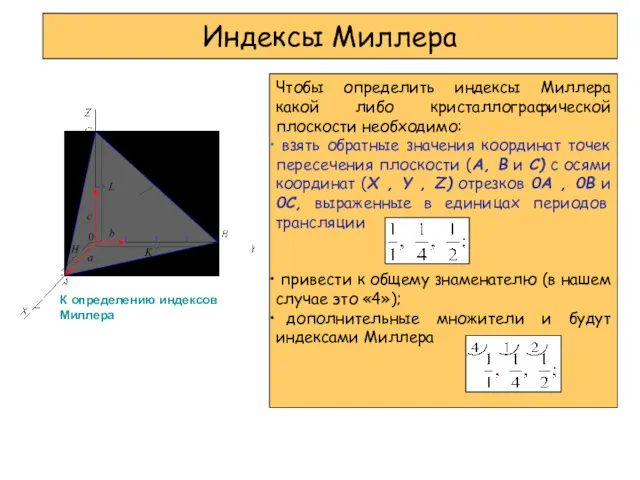
- 14. Индексы Миллера Чтобы определить индексы Миллера какой либо кристаллографической плоскости необходимо: взять обратные значения координат точек
- 15. Изобразите плоскость с индексами В этом случае сначала придется выполнить задачу, обратную предыдущей, поскольку предварительно надобно
- 16. Найдите индексы плоскости, отсекающей на координатных осях отрезки: 2; -1; - 1/2. 1. Искомая плоскость отсекает
- 17. В кристалле всегда можно выделить плоскости, которые параллельны одному направлению в пространстве. При параллельном переносе все
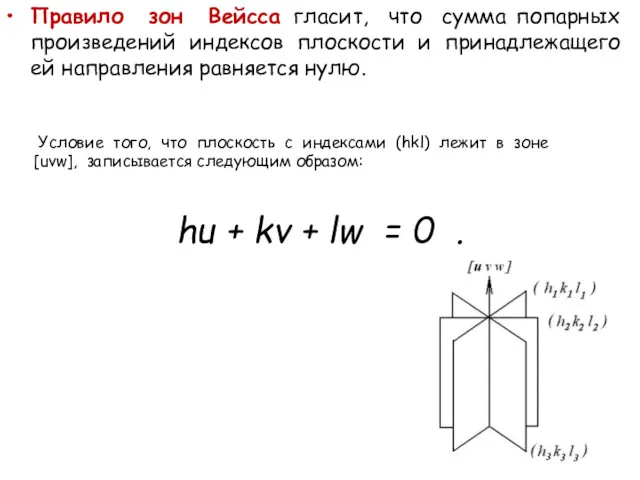
- 18. Правило зон Вейсса гласит, что сумма попарных произведений индексов плоскости и принадлежащего ей направления равняется нулю.
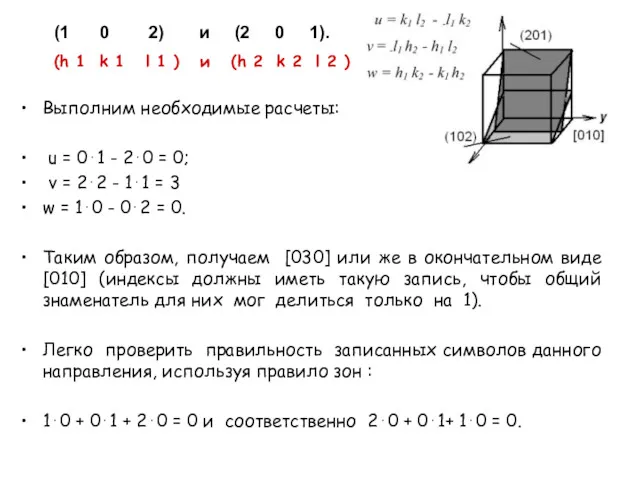
- 19. Определите ось зоны для следующих пересекающихся плоскостей: (102) и (201). Дайте изображение этих плоскостей и оси
- 20. Выполним необходимые расчеты: u = 0⋅1 - 2⋅0 = 0; v = 2⋅2 - 1⋅1 =
- 21. Какие из перечисленных ниже плоскостей могут входить в кристаллографическую зону [-1 1 1]: (100); (110); (101);
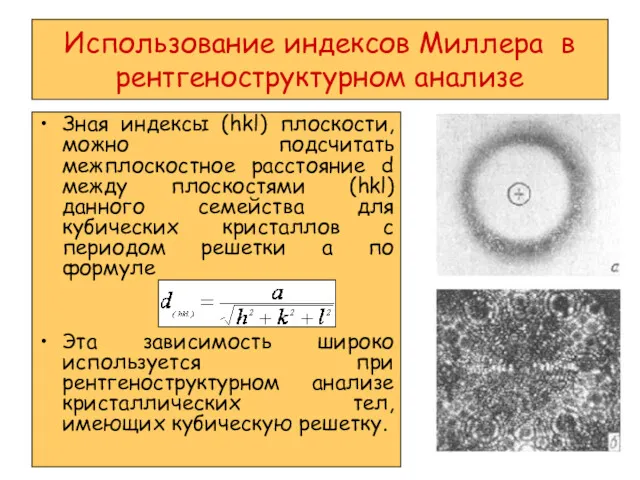
- 22. Использование индексов Миллера в рентгеноструктурном анализе Зная индексы (hkl) плоскости, можно подсчитать межплоскостное расстояние d между
- 23. Основой рентгеноструктурного анализа является формула Вульфа — Брэггов, показывающая условия интерференции отраженных рентгеновских лучей от атомов
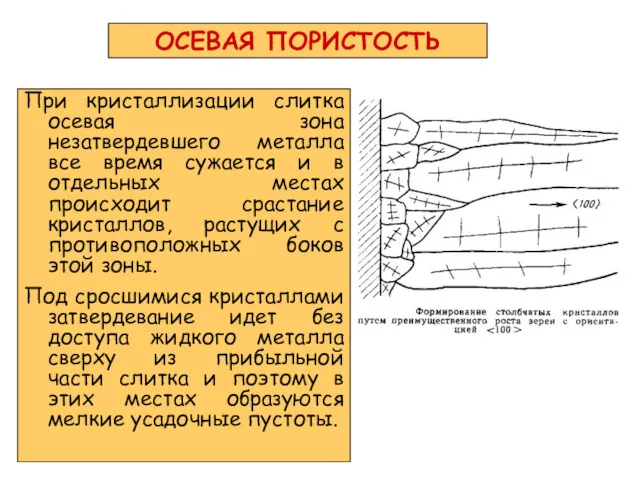
- 24. ОСЕВАЯ ПОРИСТОСТЬ При кристаллизации слитка осевая зона незатвердевшего металла все время сужается и в отдельных местах
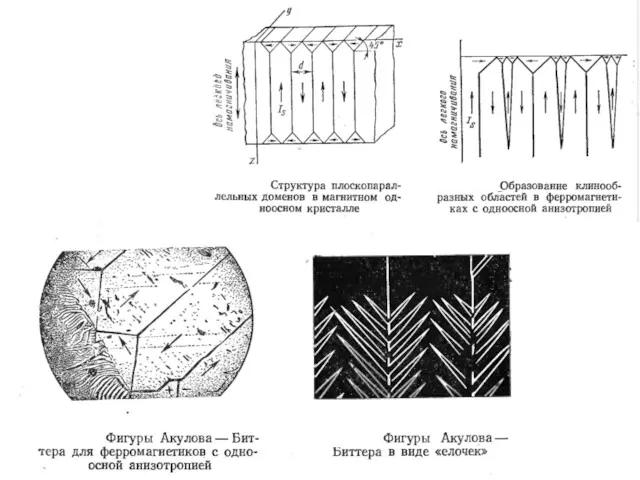
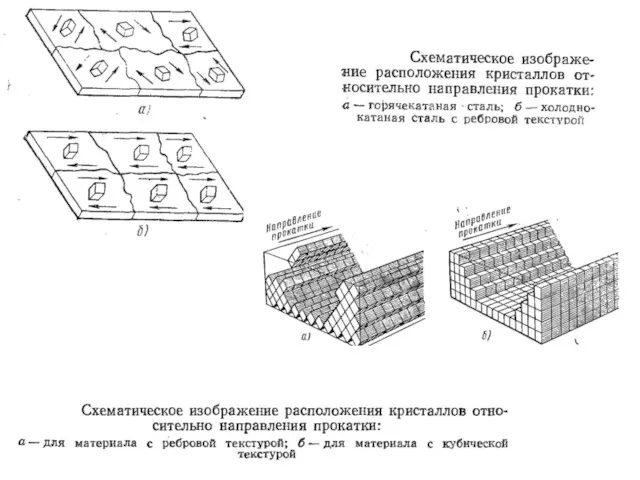
- 26. Домены
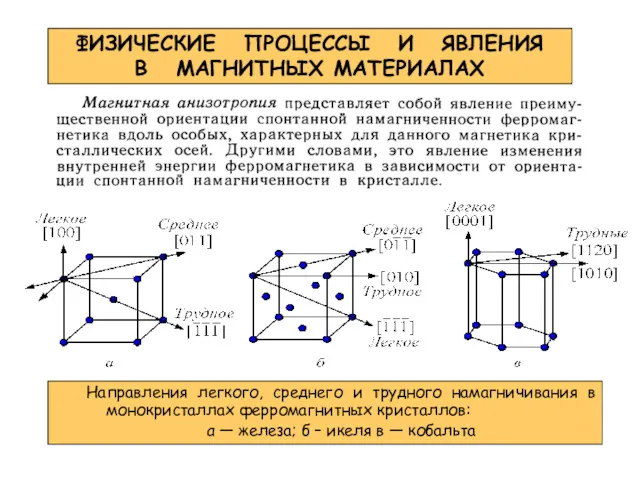
- 28. ФИЗИЧЕСКИЕ ПРОЦЕССЫ И ЯВЛЕНИЯ В МАГНИТНЫХ МАТЕРИАЛАХ Направления легкого, среднего и трудного намагничивания в монокристаллах ферромагнитных
- 29. рисунке ФИЗИЧЕСКИЕ ПРОЦЕССЫ И ЯВЛЕНИЯ В МАГНИТНЫХ МАТЕРИАЛАХ Кривые намагничивания кристаллов железа и никеля вдоль различны»
- 32. Скачать презентацию











 Давление. Единицы давления. Способы уменьшения и увеличения давления
Давление. Единицы давления. Способы уменьшения и увеличения давления Двигатели внутреннего сгорания
Двигатели внутреннего сгорания Фізичні характеристики Сонця
Фізичні характеристики Сонця Способ установки фаркопа для легковых автомобилей категории М1 и его сертификация
Способ установки фаркопа для легковых автомобилей категории М1 и его сертификация Импульс, закон сохранения импульса
Импульс, закон сохранения импульса ИК-спектроскопия
ИК-спектроскопия Электромагнитное излучение. Свойства излучения Электромагнитное излучение, исследуемое в астрофизике
Электромагнитное излучение. Свойства излучения Электромагнитное излучение, исследуемое в астрофизике Механика твердого тела. (Лекция 4)
Механика твердого тела. (Лекция 4) Физические основы воздействия на атмосферные процессы. Реагенты
Физические основы воздействия на атмосферные процессы. Реагенты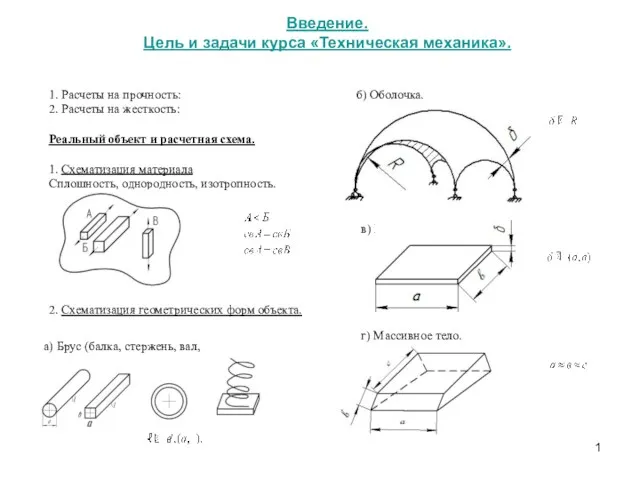 Цель и задачи курса Техническая механика. Расчеты на прочность. Расчеты на жесткость
Цель и задачи курса Техническая механика. Расчеты на прочность. Расчеты на жесткость Электронная презентация Изопроцессы в идеальном газе
Электронная презентация Изопроцессы в идеальном газе Теплотехника. Термодинамика открытых систем
Теплотехника. Термодинамика открытых систем Электрический ток в металлах. Электролитическая диссоциация. Электролиз
Электрический ток в металлах. Электролитическая диссоциация. Электролиз Энергия. Работа. Мощность
Энергия. Работа. Мощность NW Rapid Site Installation
NW Rapid Site Installation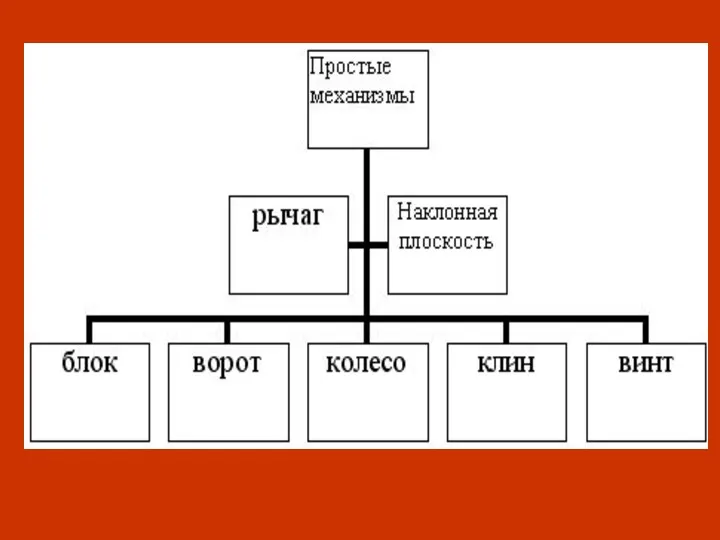 Простые механизмы
Простые механизмы Гетерогенный химический процесс система газ твердое
Гетерогенный химический процесс система газ твердое Стоячие волны
Стоячие волны Конспект урока по физике в 7 классе Сообщающиеся сосуды
Конспект урока по физике в 7 классе Сообщающиеся сосуды Сила трения
Сила трения Механизмы переноса тепла: теплопроводность, конвекция, излучение
Механизмы переноса тепла: теплопроводность, конвекция, излучение Сила трения. Особенности сил трения
Сила трения. Особенности сил трения Закон сохранения энергии, 7 класс
Закон сохранения энергии, 7 класс Огляд конструкцій плугів спец. призначення. Огляд конструкцій фрезерних машин, ямокопачів, площадкоутворювачів. Лекція 4 (ч. 2)
Огляд конструкцій плугів спец. призначення. Огляд конструкцій фрезерних машин, ямокопачів, площадкоутворювачів. Лекція 4 (ч. 2) Ремонт и сборка зубчатых передач
Ремонт и сборка зубчатых передач Система единиц СИ. Векторные и скалярные величины
Система единиц СИ. Векторные и скалярные величины Основні закономірності термодинаміки. Термостатика та термодинаміка. Лекція 1
Основні закономірності термодинаміки. Термостатика та термодинаміка. Лекція 1 Ректификация үдерісі
Ректификация үдерісі