Содержание
- 2. (12.1.1) (12.1.2)
- 3. (12.1.3)
- 5. (12.2.1)
- 8. (12.2.4)
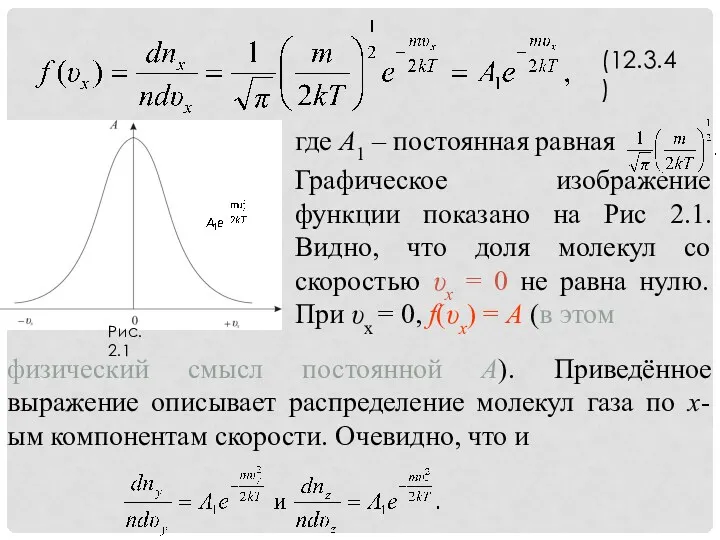
- 10. (12.3.4)
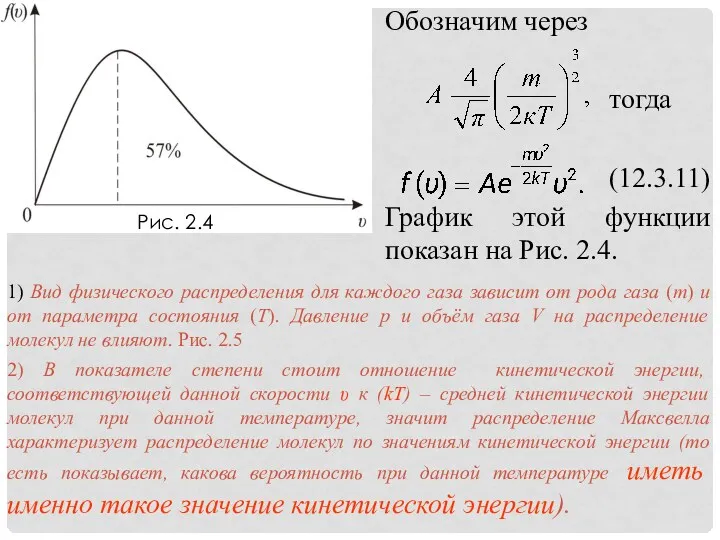
- 11. (12.3.5)
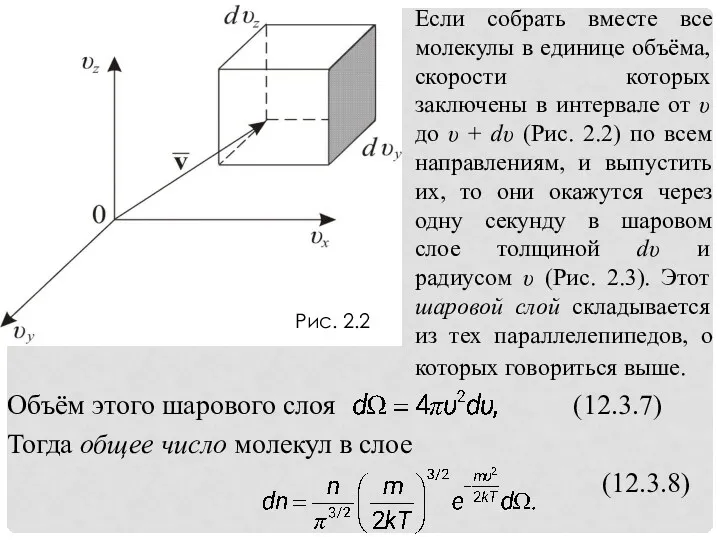
- 12. Рис. 2.2
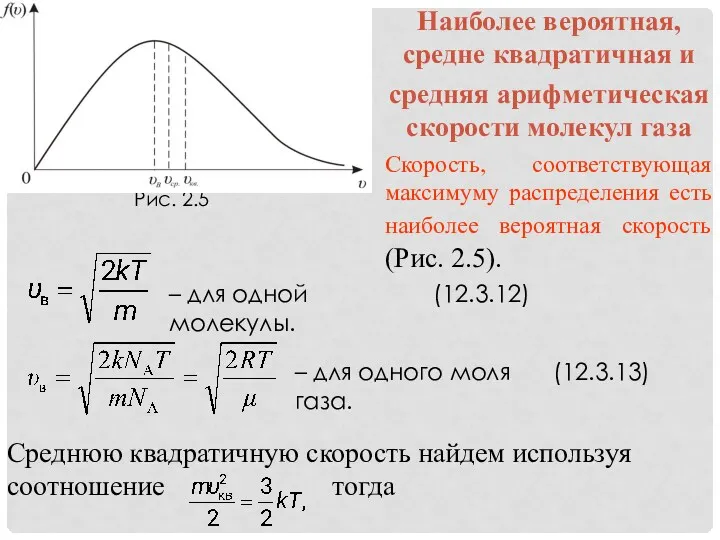
- 15. – для одной молекулы. (12.3.12) – для одного моля газа. (12.3.13)
- 16. – для одной молекулы. (12.3.14) – для одного моля газа. (12.3.15) Средняя арифметическая скорость − υср
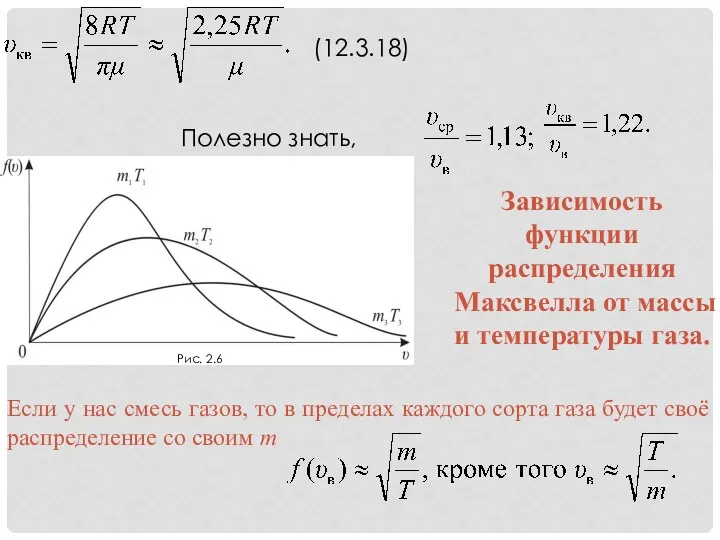
- 17. (12.3.18) Полезно знать, что
- 19. (12.3.20)
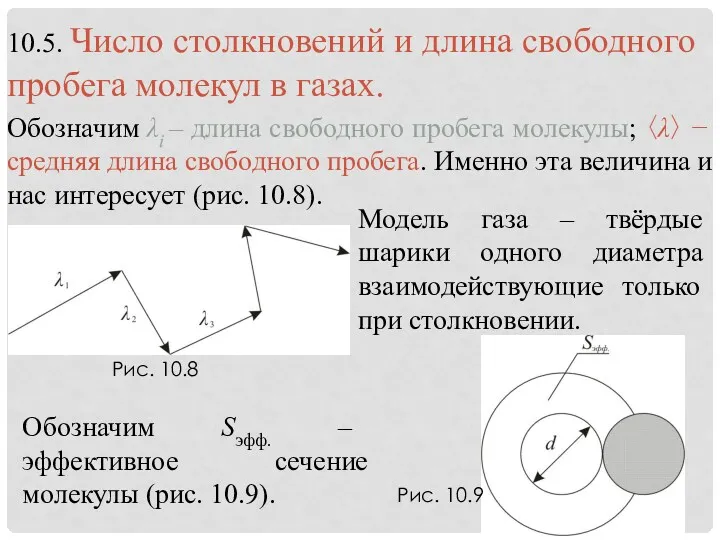
- 21. Рис. 10.8 Рис. 10.9
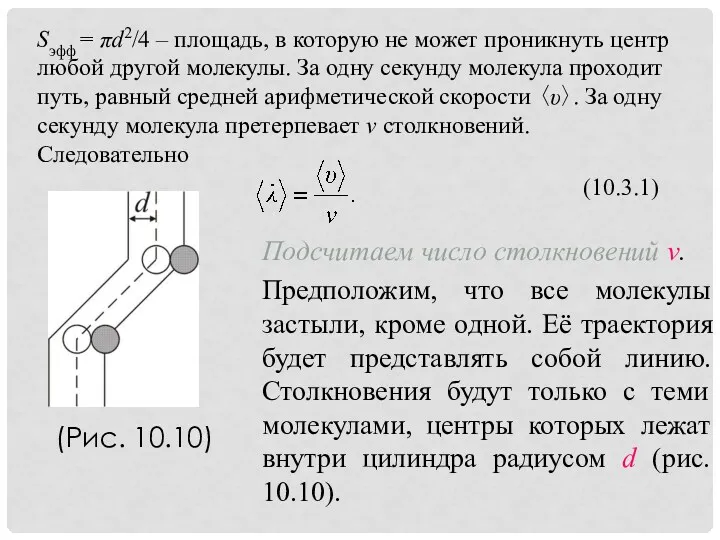
- 22. (Рис. 10.10)
- 23. (10.3.3) А так как то получим (10.3.4) Так как p = nkT, то есть то (10.3.5)
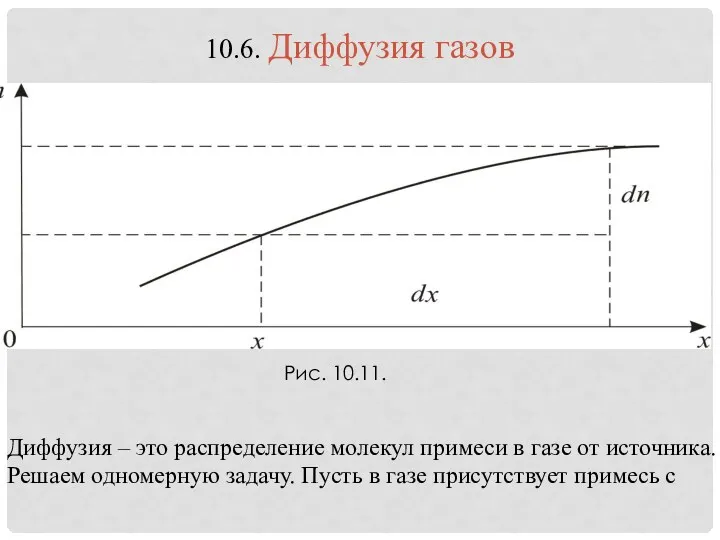
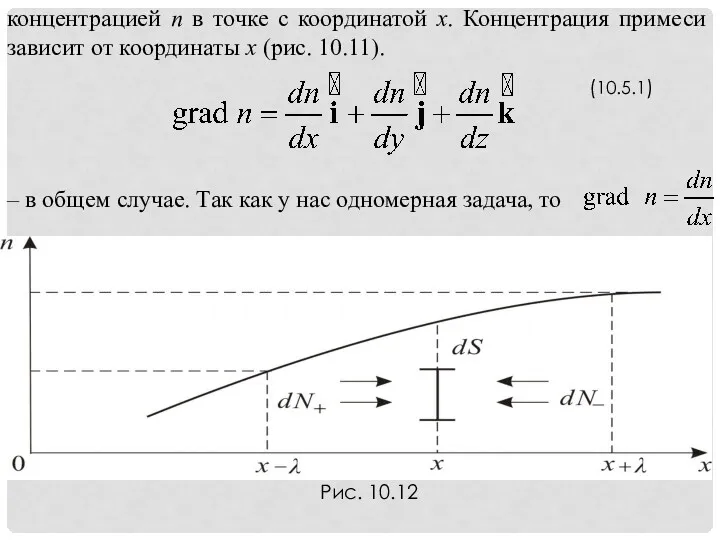
- 26. Диффузия – это распределение молекул примеси в газе от источника. Решаем одномерную задачу. Пусть в газе
- 27. (10.5.1) – в общем случае. Так как у нас одномерная задача, то
- 28. При наличии grad n, хаотическое движение будет более направленным – стремиться выровняться по концентрации и возникнет
- 29. где − концентрация молекул слева от площади, а − концентрация молекул справа от площади. (10.5.4)
- 30. Подставив это в выражение (10.5.4), получим, что (10.5.5) Сравнение выражения 10.5.5) с формулой 10.4.1) показывает, что
- 31. (13.3.7) или в общем случае (в трёх мерной системе) N = – D grad n S
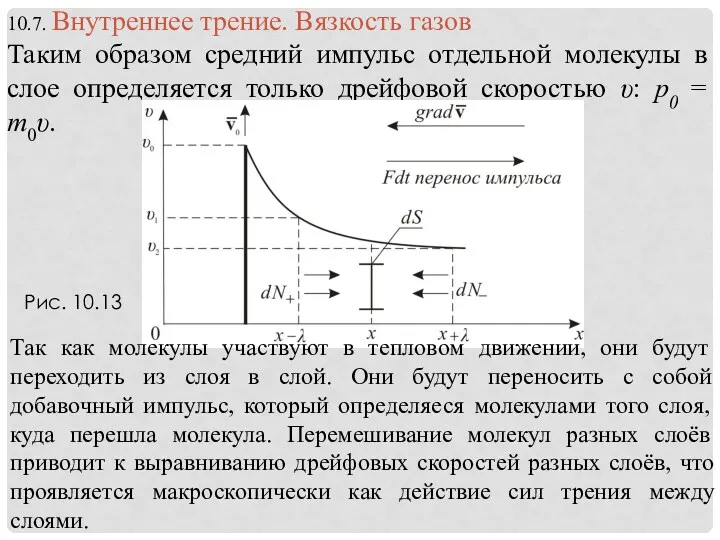
- 32. Рис. 10.13 Так как молекулы участвуют в тепловом движении, они будут переходить из слоя в слой.
- 33. Вернёмся к рис. υ(х) и рассмотрим элементарную площадку dS перпендикулярно оси х. Через эту площадку за
- 34. Приняв во внимание, что произведение nm равно плотности газа , можно записать (10.7.4) (10.7.5) Это уравнение
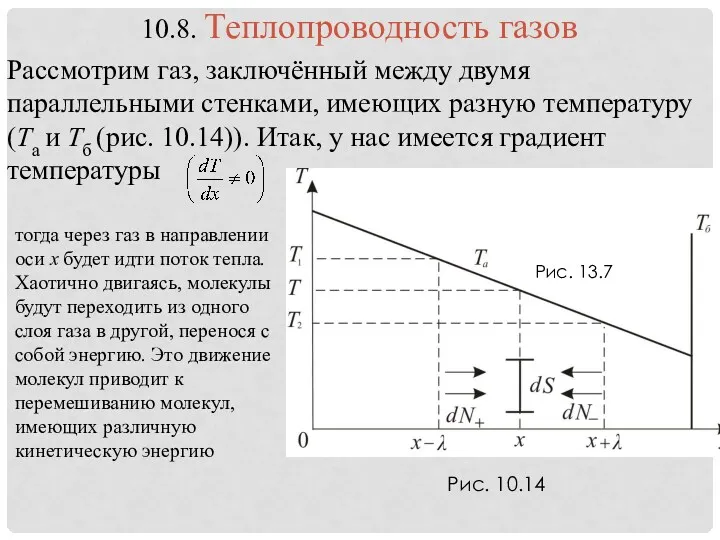
- 35. Рис. 13.7 Рис. 10.14
- 36. При подсчёте потока тепла введём следующие упрощения: 1) 〈υ〉 = const (средне арифметическая скорость). 2) Примем,
- 37. (10.8.5)
- 38. (10.8.6)
- 39. N = −D gradU или Уравнение Фика для диффузии; K = −η gradu или Уравнение Ньютона
- 41. Скачать презентацию



























 Будова атома. Склад атомних ядер. Протонне та нуклонне число
Будова атома. Склад атомних ядер. Протонне та нуклонне число Законы механики Ньютона
Законы механики Ньютона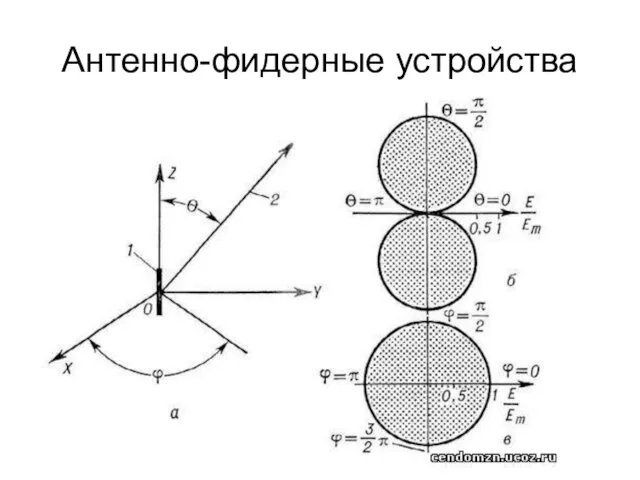 Антенно-фидерные устройства
Антенно-фидерные устройства Радиоактивтілік. Сәуле шығару. Элементар бөлшектерді тіркеу мен бақылау әдістері
Радиоактивтілік. Сәуле шығару. Элементар бөлшектерді тіркеу мен бақылау әдістері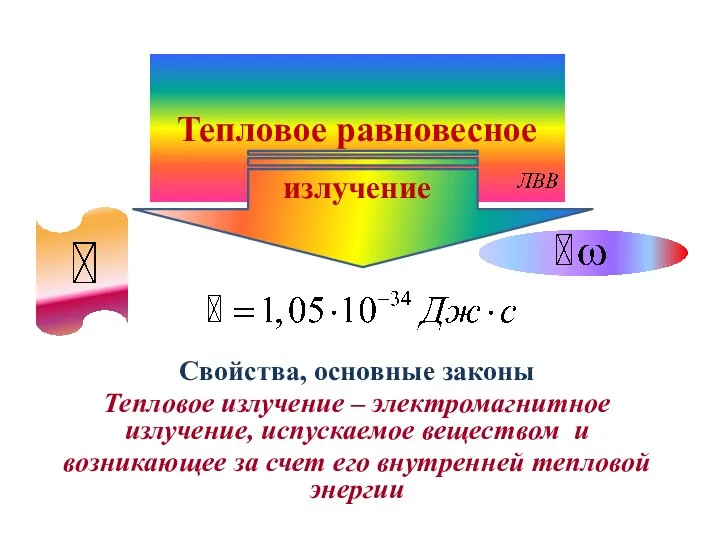 Тепловое равновесное излучение. Лекция 1
Тепловое равновесное излучение. Лекция 1 Средства контроля
Средства контроля Презентация Физика в загадках
Презентация Физика в загадках Основы электродинамики
Основы электродинамики Бұралған білік үшін беріктік шарты
Бұралған білік үшін беріктік шарты Сила. Графічне зображення сил
Сила. Графічне зображення сил Давление газа и твердых тел
Давление газа и твердых тел Қатты дене-сұйық жанасу шегіндегі адсорбция
Қатты дене-сұйық жанасу шегіндегі адсорбция Судовые аккумуляторы
Судовые аккумуляторы Система охлаждения с заданными значениями
Система охлаждения с заданными значениями Технические изобретения 17,18,19 и начало 20 века
Технические изобретения 17,18,19 и начало 20 века Термическая обработка
Термическая обработка Главные схемы электрических соединений электроустановок. (Лекция 11)
Главные схемы электрических соединений электроустановок. (Лекция 11) Квантовые постулаты Бора
Квантовые постулаты Бора Простые механизмы
Простые механизмы Презентация по физике на тему:Солнечная батарея и ее использование в физике
Презентация по физике на тему:Солнечная батарея и ее использование в физике Свободное падение.
Свободное падение. Работа силы. Мощность. Теория №9
Работа силы. Мощность. Теория №9 Оптика. Световые явления. (Урок 29 -30)
Оптика. Световые явления. (Урок 29 -30) Полупроводниковые диоды
Полупроводниковые диоды Система охлаждения двигателя внутреннего сгорания
Система охлаждения двигателя внутреннего сгорания Явление электромагнитной индукции. Магнитный поток. Закон электромагнитной индукции.
Явление электромагнитной индукции. Магнитный поток. Закон электромагнитной индукции. Движение тел под действием силы тяжести
Движение тел под действием силы тяжести Физические основы оптической локации
Физические основы оптической локации