Мпр=0 – момент на правой опоре С правого пролета ВС,
Раскрыть
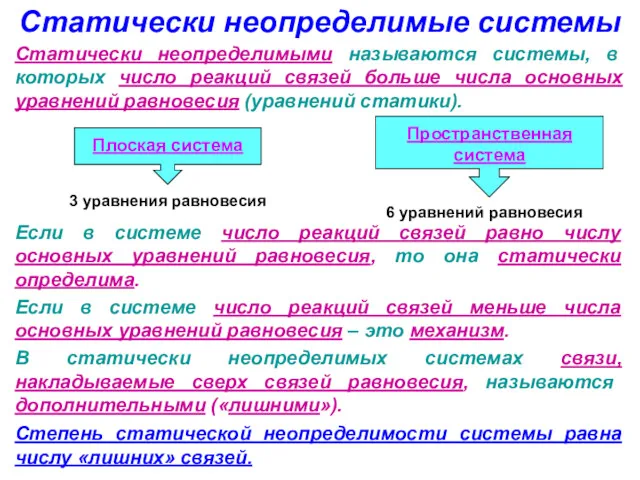
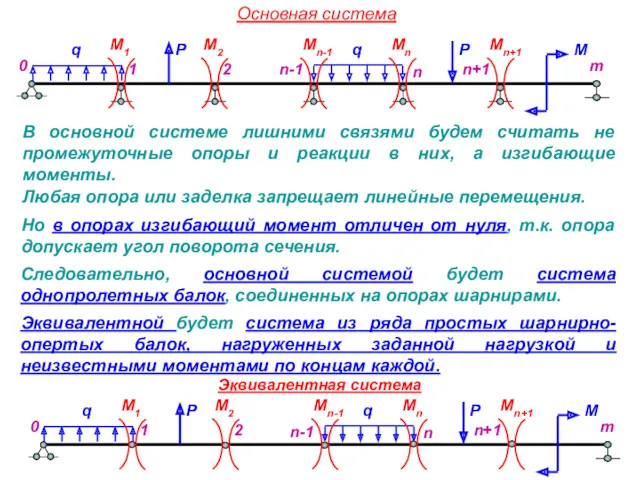
статическую неопределимость двухпролетной балки.
Система один раз статически неопределима:
4 неизвестные опорные реакции: RA ,RB ,RC ,HC
1 степень статической неопределимости,
Пример.
3 основных уравнения равновесия
-
Ωл = 0
lл=l – длина левого пролета АВ,
Мл=0 – момент на левой опоре А левого пролета АВ,
2 Мср = 2МВ – удвоенный момент на средней опоре,
lпр=l – длина правого пролета ВС,
Ωл = 0
– площадь грузовой эпюры моментов под левым пролетом,
– площадь грузовой эпюры моментов под правым пролетом,
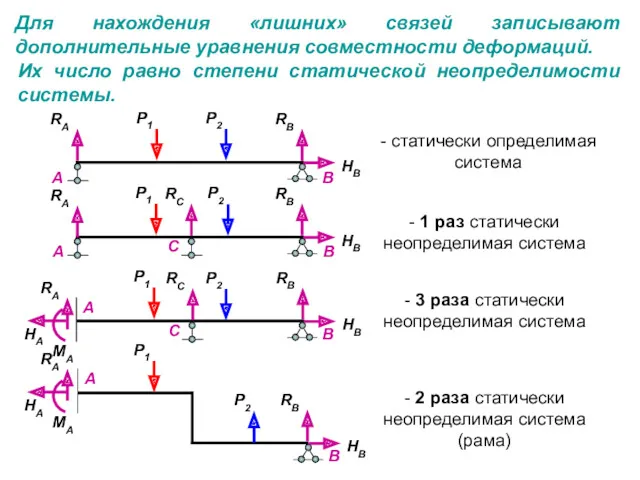
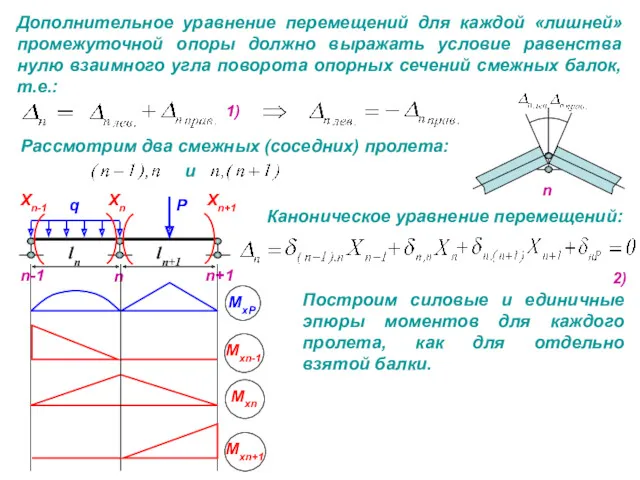
Врезаем мысленно шарнир в точке В в ось балки и рассматриваем каждый пролет, как отдельно взятую статически определимую балку.
Левый пролет АВ пустой, под правым пролетом ВС выстраиваем грузовую эпюру изгибающего момента МхР .
необходимо записать одно уравнение 3-х моментов:
ал= 0
– расстояние от центра тяжести Ωл до левой опоры А левого пролета АВ,
bпр= l/2
– расстояние от центра тяжести Ωпр до правой опоры С правого пролета ВС.
0·l + 2МВ ( l + l ) + 0·l + 6 (
) = 0
или:
4МВ l +
откуда:
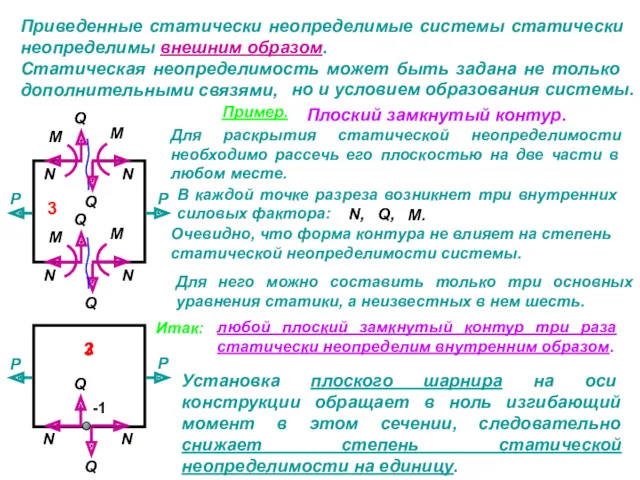
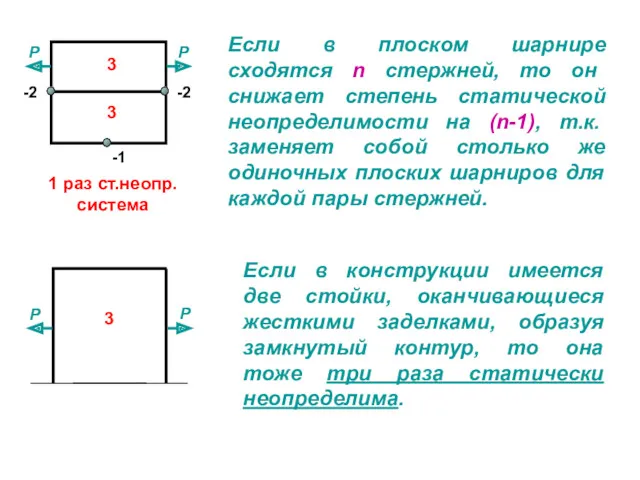
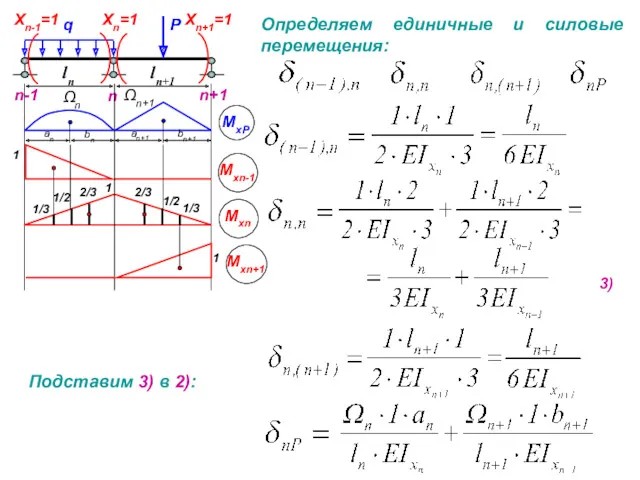
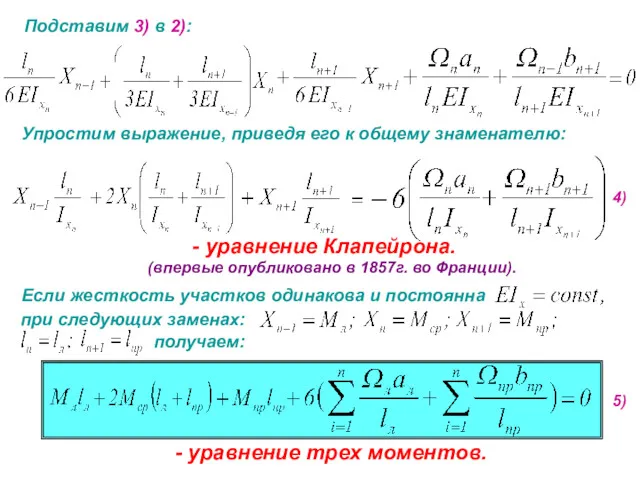
Снова рассмотрим каждый пролет, как отдельно взятую статически определимую балку с найденным моментом МВ , учитывая его знак.
Строим эпюры Qy и Мх под каждым пролетом отдельно.






 Загадки непростые, а с подсказками
Загадки непростые, а с подсказками Электрическая цепь и ее составные части
Электрическая цепь и ее составные части Система сходящихся сил. Момент силы. Лекция 2
Система сходящихся сил. Момент силы. Лекция 2 Умники и умницы
Умники и умницы Закон сохранения и превращения механической энергии
Закон сохранения и превращения механической энергии Кількість теплоти, що виділяється в провіднику зі струмом
Кількість теплоти, що виділяється в провіднику зі струмом Cummins Engine Company LTD
Cummins Engine Company LTD Гідростатичний тиск
Гідростатичний тиск Физические основы механики. Лекция 1.1
Физические основы механики. Лекция 1.1 Технический проекты Леонардо да Винчи
Технический проекты Леонардо да Винчи Взаимодействие ионизирующего излучения с веществом
Взаимодействие ионизирующего излучения с веществом Испарение и конденсация. Кипение жидкости
Испарение и конденсация. Кипение жидкости Решение задач по теме Основы термодинамики
Решение задач по теме Основы термодинамики Основы квантовой физики. Лазеры
Основы квантовой физики. Лазеры Методы повышения эффективности усвоения понятий при изучении темы динамика
Методы повышения эффективности усвоения понятий при изучении темы динамика Основные понятия в теории механизмов и машин. ТММ Лекция 1
Основные понятия в теории механизмов и машин. ТММ Лекция 1 Методы синтеза САУ
Методы синтеза САУ Шпоночные и шлицевые соединения
Шпоночные и шлицевые соединения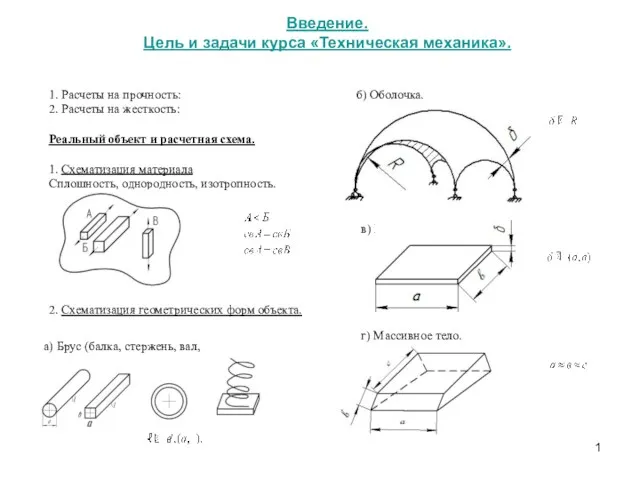 Цель и задачи курса Техническая механика. Расчеты на прочность. Расчеты на жесткость
Цель и задачи курса Техническая механика. Расчеты на прочность. Расчеты на жесткость Стальные и растительные тросы
Стальные и растительные тросы Простые механизмы.4 класс
Простые механизмы.4 класс Синергетика – новое междисциплинарное научное направление
Синергетика – новое междисциплинарное научное направление Дизель 10 Д 100
Дизель 10 Д 100 Устройство, принцип работы системы питания карбюраторного двигателя
Устройство, принцип работы системы питания карбюраторного двигателя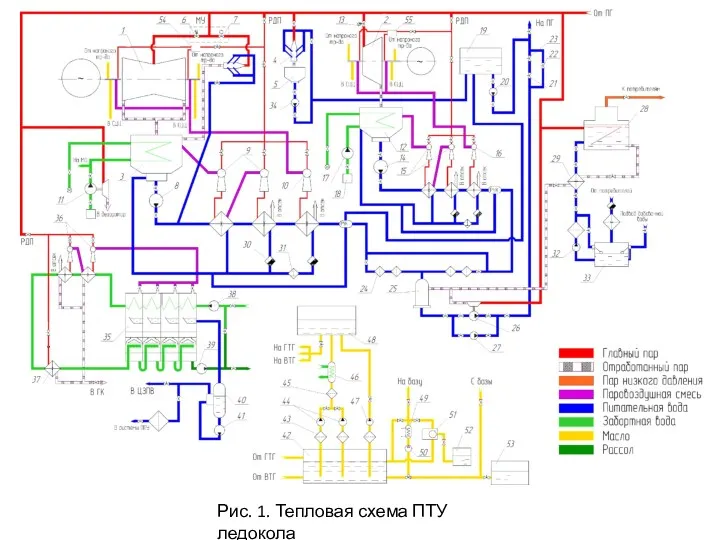 Системы ПТУ 2
Системы ПТУ 2 Связанные волны в нелинейной среде
Связанные волны в нелинейной среде Выталкивающая сила
Выталкивающая сила Измерение влажности
Измерение влажности