Теория упругости сплошных сред. Упругие поля (поля напряжений) вокруг дислокаций. Энергия дислокаций презентация
Содержание
- 2. Типы дислокаций: Краевые дислокации - Edge Dislocation: A portion of an extra plane of atoms Винтовые
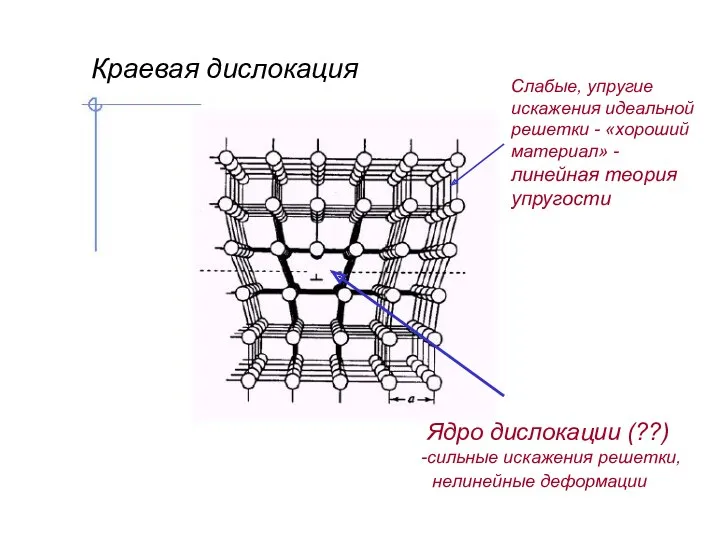
- 3. Ядро дислокации (??) сильные искажения решетки, нелинейные деформации Краевая дислокация Слабые, упругие искажения идеальной решетки -
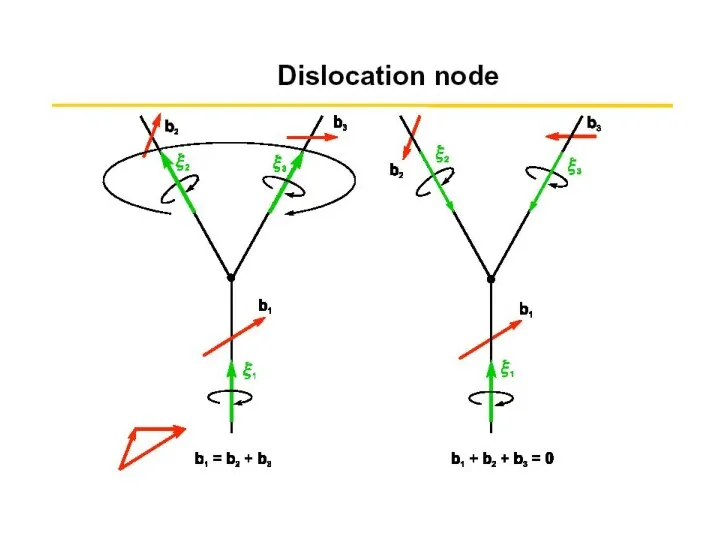
- 4. Свойства вектора Бюргерса Finish-start/ right hand
- 5. Свойства дислокаций Дислокационная линия не может закончиться внутри кристалла, а только - на его поверхности -
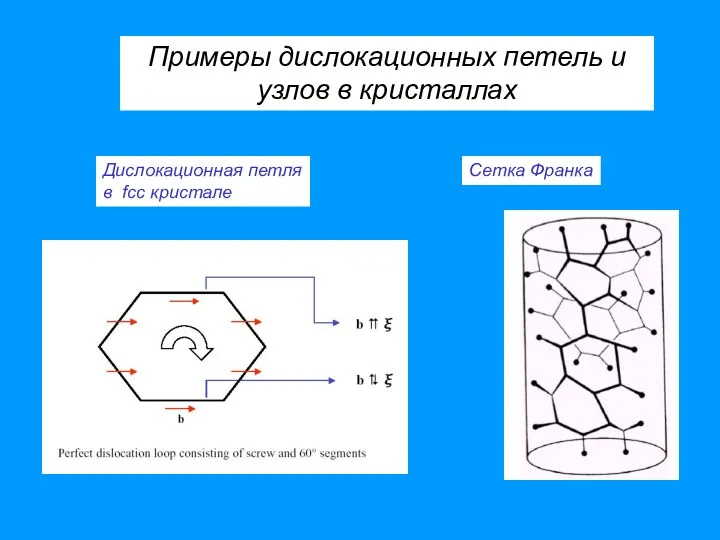
- 7. Сетка Франка Дислокационная петля в fcc кристале Примеры дислокационных петель и узлов в кристаллах
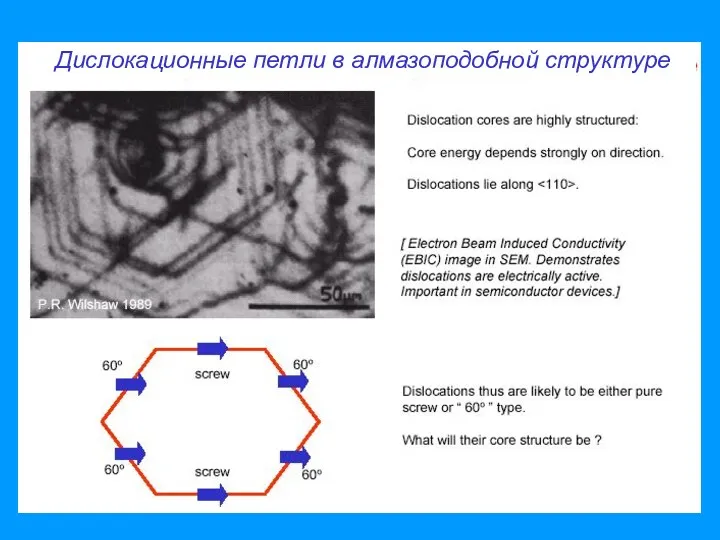
- 8. Дислокационные петли в алмазоподобной структуре
- 9. ρ -1/2 Плотность дислокаций Определение плотности дислокаций Выражается в единицах, см-2 Типичные значения в отожженных металлах
- 10. Элементы теории упругости сплошных сред
- 11. Закон Гука, модуль Юнга Y ≡ E Брусок из однородного изотропного материала
- 12. Коэффициент Пуассона В кристаллах: σ ij = Cijkl εkl
- 13. Брусок под действием гидростатического давления
- 15. Объемный модуль упругости
- 16. Однородный сдвиг (1) клей
- 17. Однородный сдвиг (2) ∑Fi = 0 ∑Mi = 0
- 18. Однородный сдвиг (3) сдвиге
- 19. -1 Однородный сдвиг (4)
- 20. Элементы теории упругости кристаллов
- 22. σij = dFi /dAj
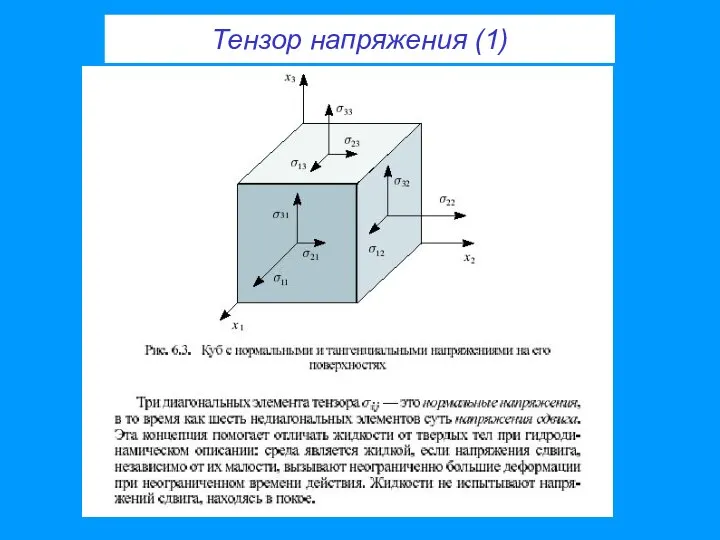
- 24. Тензор напряжения (1)
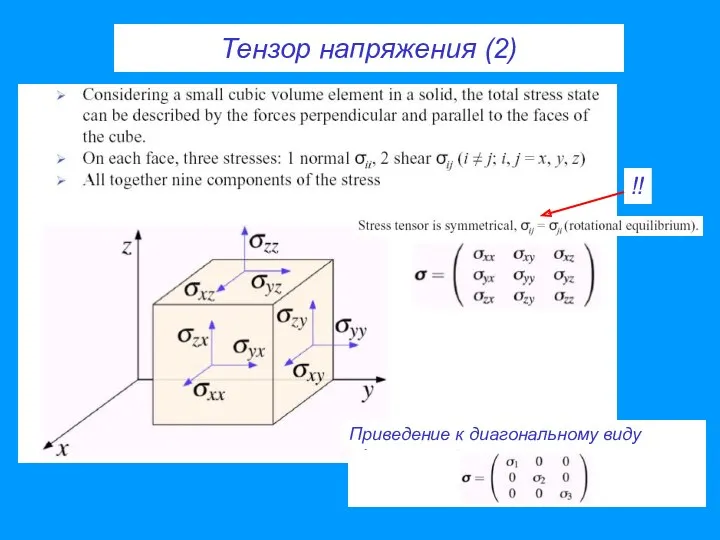
- 25. Тензор напряжения (2) Приведение к диагональному виду !!
- 26. σij Симметрия тензора напряжения σij
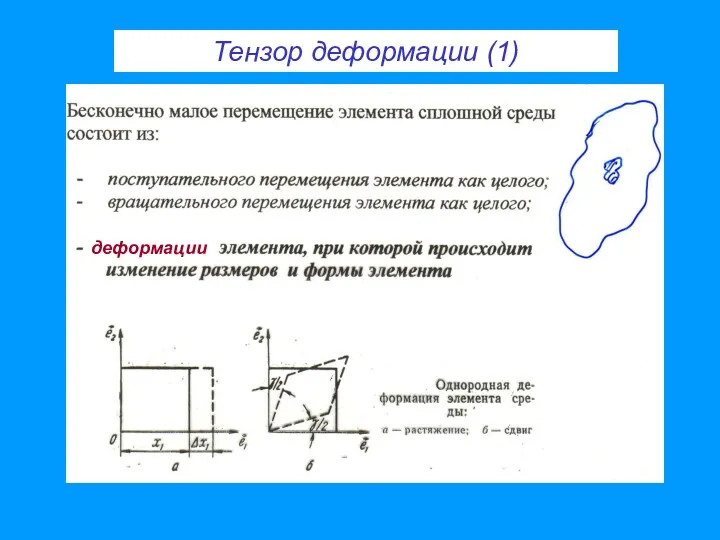
- 27. Тензор деформации (1) деформации
- 28. Тензор деформации (2) u - смещение частицы e = lim (Δ x’ - Δ x)/ Δ
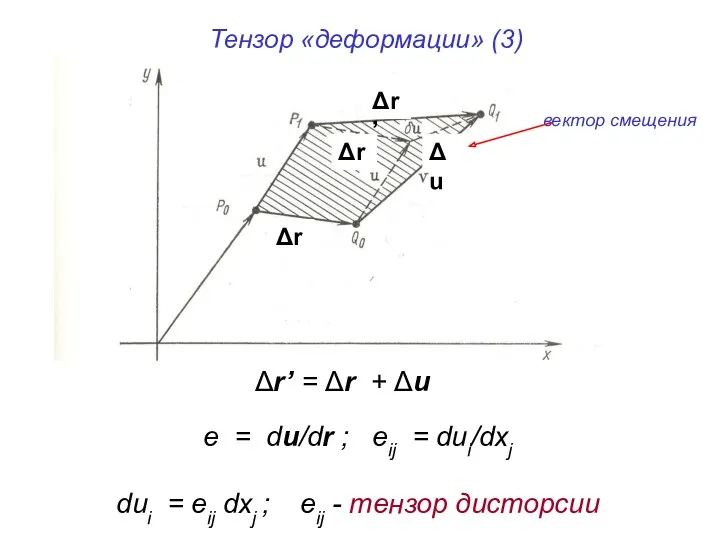
- 29. Тензор «деформации» (3) Δr’ Δr Δr Δu Δr’ = Δr + Δu e = du/dr ;
- 30. Тензор дисторсии (1)
- 31. В общем случае: Δ r’ = Δ r + Δ u e = du/dr ; eij
- 32. Тензор дисторсии (2) 2
- 33. Определение тензора деформации - Тензор деформации - Чистые повороты
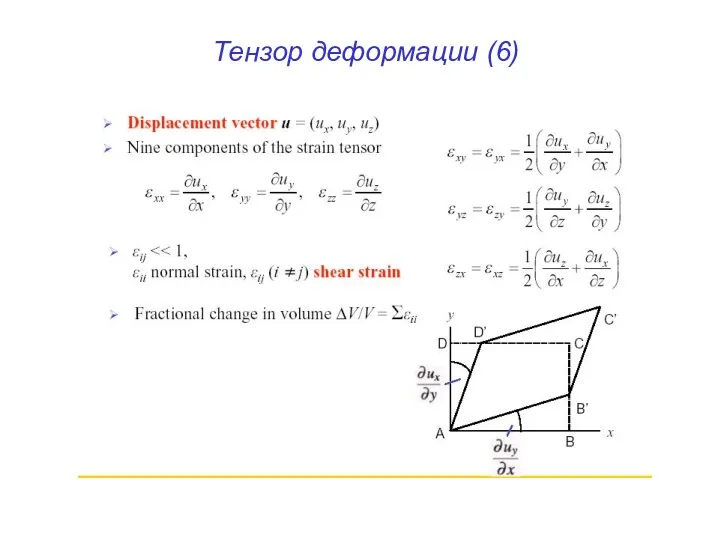
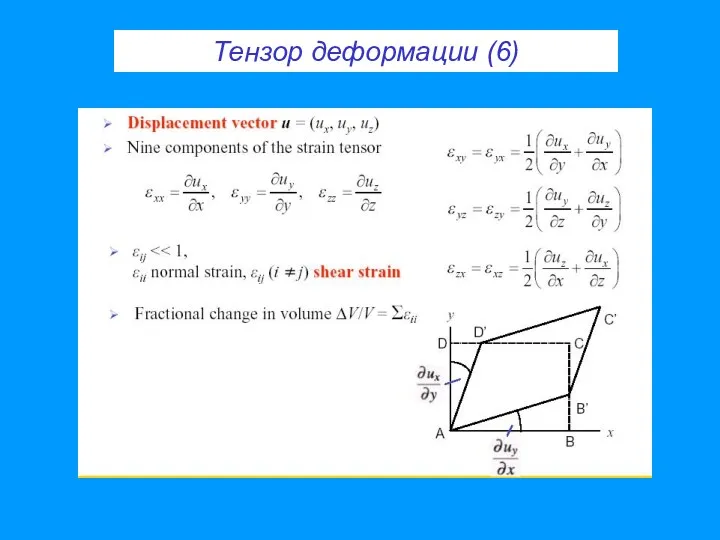
- 34. Тензор деформации (6)
- 35. Δr’ = Δr + Δu (Δr’)2 = (Δr)2 + 2Δr Δu + Δu2 (Δr’)2 - (Δr)2
- 36. Δr Δr’ Δu = ω x Δr Акивис, Гольдберг, 1969
- 37. Акивис, Гольдберг, 1969
- 39. Тензор деформации (5)
- 40. Тензор деформации (6)
- 41. Тензор упругости σij σij = Cijkl εkl σij σij
- 42. Роль симметрии В кубических кристаллах достаточно трех упругих констант Кубические кристаллы Ромбическая Тригональная
- 43. Изотропное твердое тело μ ≡ G E = 2G (1+ ν) ν = λ/2(λ +G )
- 44. Коэффициенты упругости Кубические кристаллы 1.6х10-12 Оценка величины коэффициентов упругости C11 Cijkl C C C12 C44 Дин/см2
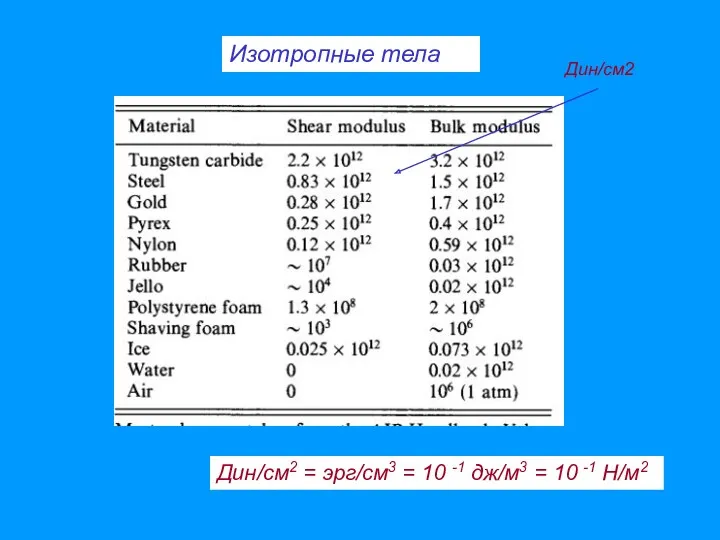
- 45. Изотропные тела Дин/см2 = эрг/см3 = 10 -1 дж/м3 = 10 -1 Н/м2 Дин/см2
- 46. Энергия деформируемого кристалла
- 47. В случае однородной деформации: εkl = const (r ) Wel полн = (1/2)Cε2 V - одноконстантное
- 48. Энергия деформируемого кристалла
- 49. В общем случае если деформация производится обратимо и при постоянной температуре, и если вся работа идет
- 50. Упругие поля и напряжения вокруг дислокаций
- 51. Дислокации в непрерывной упругой среде Построение Вольтерра
- 52. Образование краевой дислокации в кристалле
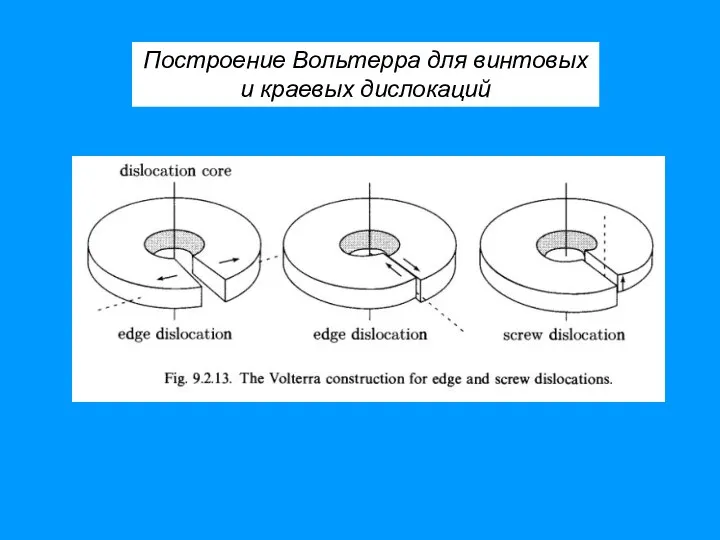
- 53. Построение Вольтерра для винтовых и краевых дислокаций
- 54. Поле смещений вокруг винтовой дислокации Цилиндрические координаты: r, θ, z x2 + y2 = r2; tgθ
- 55. Вычисление компонент тензора деформации (1) uz = uz(x,y) ux = 0 uy = 0
- 56. Вычисление компонент тензора деформации (2) Смещения: (1/2)duz/dy =(b/4π)d[ arctg(y/x)]/dy = ∫dy/(y2 +a2) = (1/a) arctg(y/a) arctg
- 57. Вычисление компонент тензора деформации (3) εxx = εyy = εzz = εxy = εyx = 0
- 58. μ ≡ G Вычисление компонент тензора напряжений
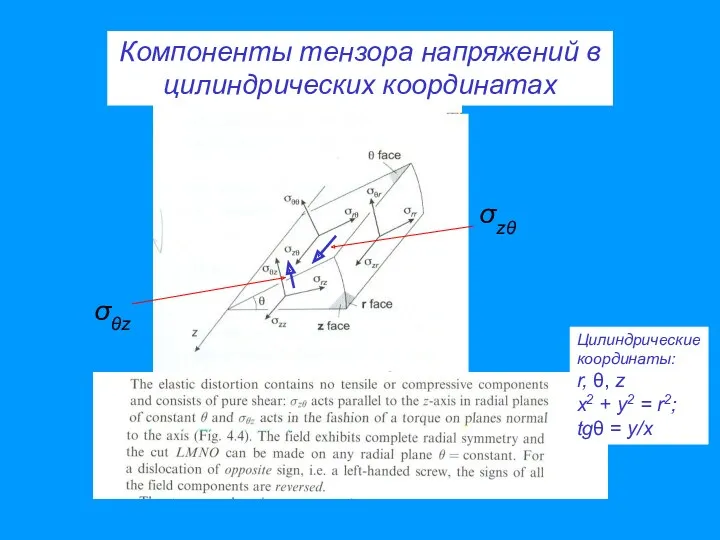
- 59. Компоненты тензора напряжений в цилиндрических координатах σθz σzθ Цилиндрические координаты: r, θ, z x2 + y2
- 60. Компоненты тензоров напряжений и деформаций в цилиндрических координатах используя соотношения: и, аналогичным образом, для сдвиговых деформаций,
- 61. Отличные от нуля компоненты εij и σkl убывают с расстоянием от дислокации как r -1, ε
- 62. Сравнение законов спадания напряжений с расстоянием r, для точечных дефектов, дислокаций и дислокационных стенок
- 63. в нем имеются внутренние напряжения, источником которых являются дислокации.
- 64. Упругая энергия дислокации Полная энергия дислокации состоит из двух частей: Плотность упругой энергии, запасенной в дислокации:
- 65. Оценки упругой энергии дислокации При обычных значениях плотности дислокаций ρ =107 см-2, среднее расстояние между ними
- 67. Наименьшей энергией обладают дислокации с наи- !!
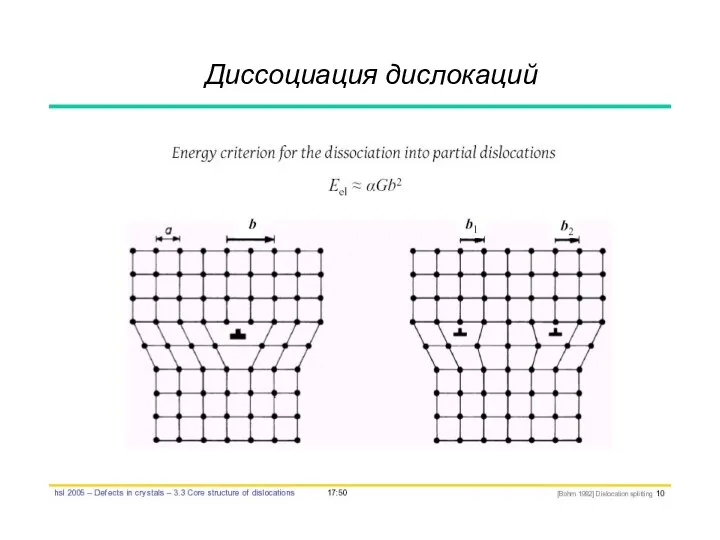
- 68. Диссоциация дислокаций
- 69. Ядро дислокации ядро – неупругие искажения упругие деформации
- 71. Скачать презентацию










































![Вычисление компонент тензора деформации (2) Смещения: (1/2)duz/dy =(b/4π)d[ arctg(y/x)]/dy =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/317692/slide-55.jpg)











 Тема 6. Электромагнитные волны
Тема 6. Электромагнитные волны Выталкивающая сила. Тест для 7 класса
Выталкивающая сила. Тест для 7 класса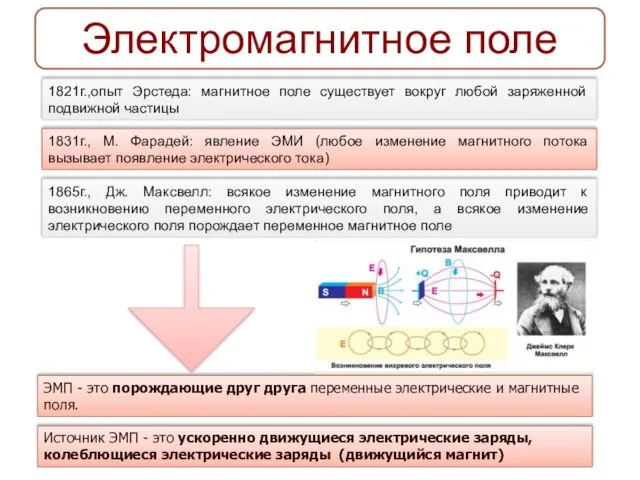 Электромагнитное поле
Электромагнитное поле Законы динамики (законы Ньютона). Лекция 5
Законы динамики (законы Ньютона). Лекция 5 Формирование логического мышления на уроках физики
Формирование логического мышления на уроках физики Конкурс учителей Есть идея!
Конкурс учителей Есть идея! Сцепление. Назначение, конструкции
Сцепление. Назначение, конструкции Закон Ома для участка электрической цепи
Закон Ома для участка электрической цепи Давление твердых тел, жидкостей и газов. Урок физики. 7 класс
Давление твердых тел, жидкостей и газов. Урок физики. 7 класс Magnit orici
Magnit orici Ауада ұшу тақырыбына презентаия
Ауада ұшу тақырыбына презентаия Элементы статистической физики. Распределение Максвелла
Элементы статистической физики. Распределение Максвелла Середня швидкість. Нерівномірний рух
Середня швидкість. Нерівномірний рух Апарати для дослідження океанічних глибин
Апарати для дослідження океанічних глибин Плоское зеркало
Плоское зеркало Физика элементарных частиц
Физика элементарных частиц Свойства воды
Свойства воды Основы теории антенн. Лекция № 6. АФУ
Основы теории антенн. Лекция № 6. АФУ Дефекты поршневой группы, оценка состояния и влияние на надежность
Дефекты поршневой группы, оценка состояния и влияние на надежность Введение в кинематику
Введение в кинематику Розв’язування задач із теми Взаємодія тіл (урок 43 - 44)
Розв’язування задач із теми Взаємодія тіл (урок 43 - 44) Основы молекулярно-кинетической теории
Основы молекулярно-кинетической теории Рефрактометрия
Рефрактометрия Дисперсные системы. Лиофобные дисперсные системы (часть 1)
Дисперсные системы. Лиофобные дисперсные системы (часть 1) Основы теории автоматического управления. Основные понятия. Лекция 7
Основы теории автоматического управления. Основные понятия. Лекция 7 Презентация к уроку физики по теме Сила тяжести.Вес тела
Презентация к уроку физики по теме Сила тяжести.Вес тела Конвективті жылу беру
Конвективті жылу беру Тепловые характеристики электротехнических материалов
Тепловые характеристики электротехнических материалов