Содержание
- 2. Ядерный магнитный резонанс ЗАВОЙСКИЙ Евгений Константинович (1907 - 1976) Реконструированная установка Е.К. Завойского (музей Е.К. Завойского
- 3. Richard R. Ernst, Switzerland Felix Bloch, USA Edward Mills Purcell, USA Isidor Isaac Rabi, USA Kurt
- 4. Общие понятия ЯМР Объекты исследования для метода ЯМР – вещества, содержащие в своём составе атомы с
- 5. Области электромагнитных излучений, используемых в аналитических методах
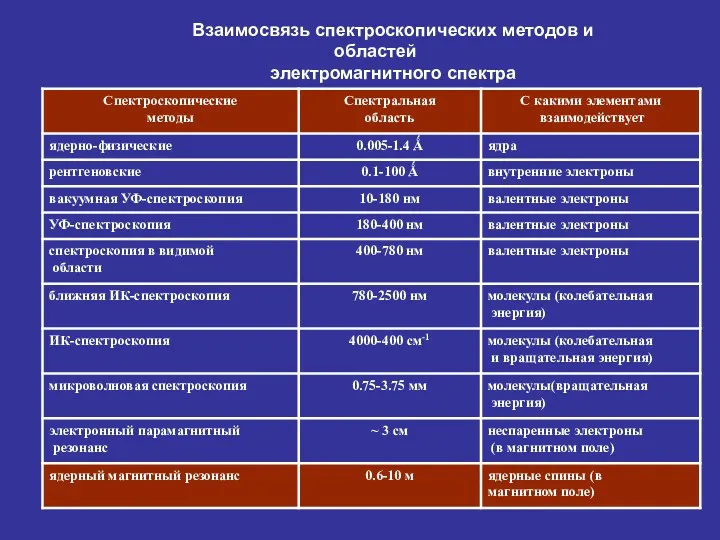
- 6. Взаимосвязь спектроскопических методов и областей электромагнитного спектра
- 7. Идентификация органических соединений. Установление или подтверждение структуры (структурно-групповой анализ). 2. Количественное определение концентрации (органических) соединений в
- 8. Состав и характеристика атомных ядер (1) Атомное ядро состоит из протонов и нейтронов (нуклонов). Эта модель
- 9. Состав и характеристика атомных ядер (2) Нейтрон (n) – электрический заряд равен нулю, а масса mn=
- 10. Состав и характеристика атомных ядер (3) Дейтрон (d) – имеет механический момент, равный сумме механических моментов
- 11. Магнитный момент ядра (1) Атомное ядро состоит из протонов и нейтронов, обладающих спином 1/2, и может
- 12. Для ядер, обладающих ненулевым спином I, магнитный момент ядра будет равен: μя = γя р =
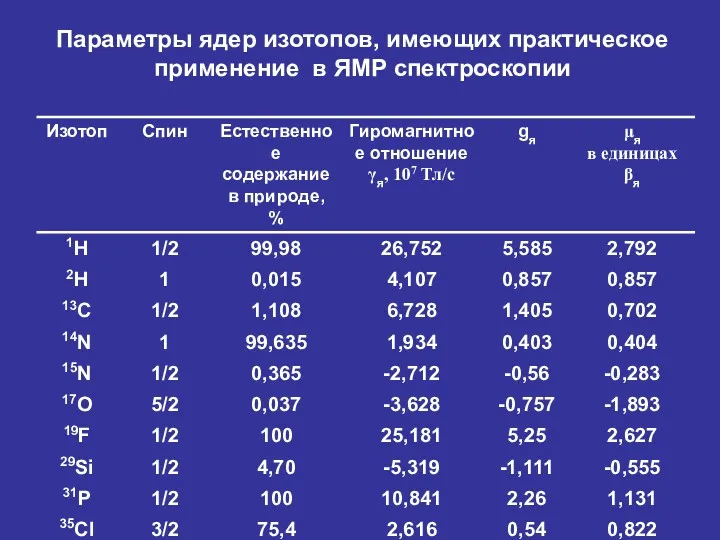
- 13. Параметры ядер изотопов, имеющих практическое применение в ЯМР спектроскопии
- 14. При наложении постоянного магнитного поля, обладающего индукцией В0 возникает взаимодействие между этим полем и магнитным моментом
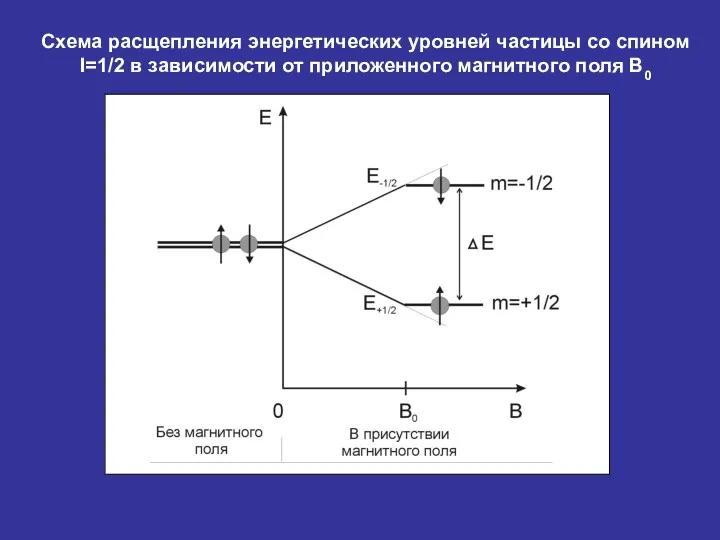
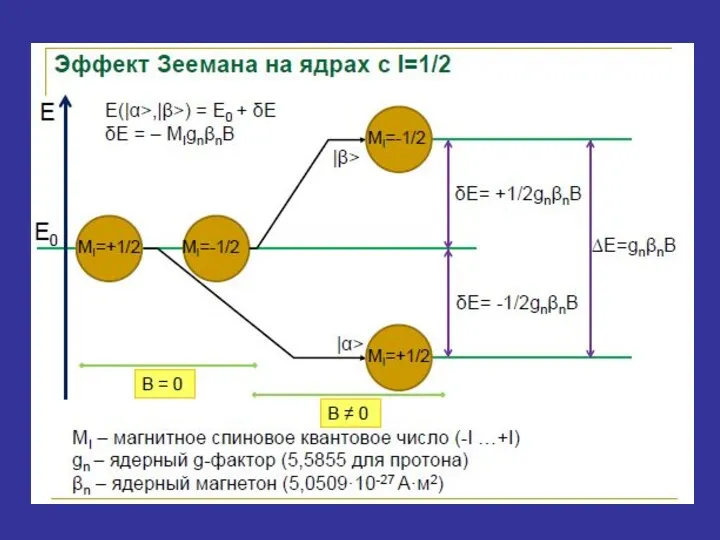
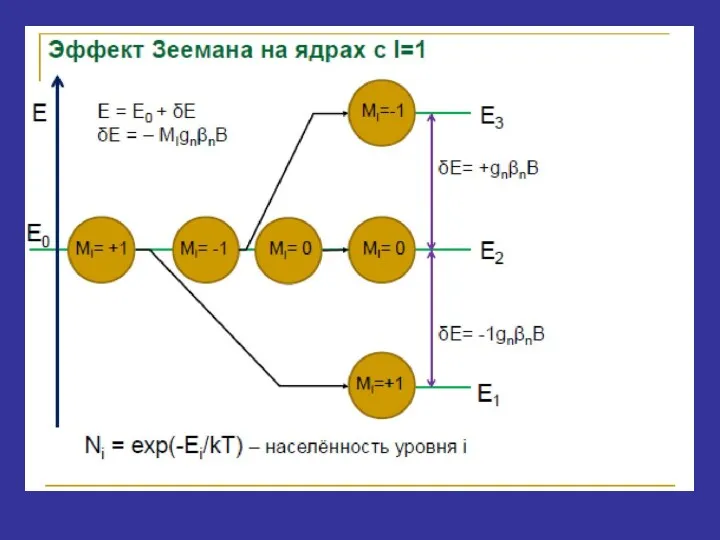
- 15. и Квантование проекции Iz, возникающее под действием приложенного магнитного поля В приводит к зеемановскому расщеплению ядерных
- 16. Схема расщепления энергетических уровней частицы со спином I=1/2 в зависимости от приложенного магнитного поля В0
- 19. где Nв,н – вероятность нахождения частицы на верхнем или нижнем уровне соответственно; k - постоянная Больцмана,
- 20. Для возбуждения переходов между расщепленными спиновыми уровнями ядра на образец, помещенный в постоянное однородное магнитное поле
- 21. Это равенство представляет собой так называемое условие ядерного магнитного резонанса. При этом для представленной на рисунке
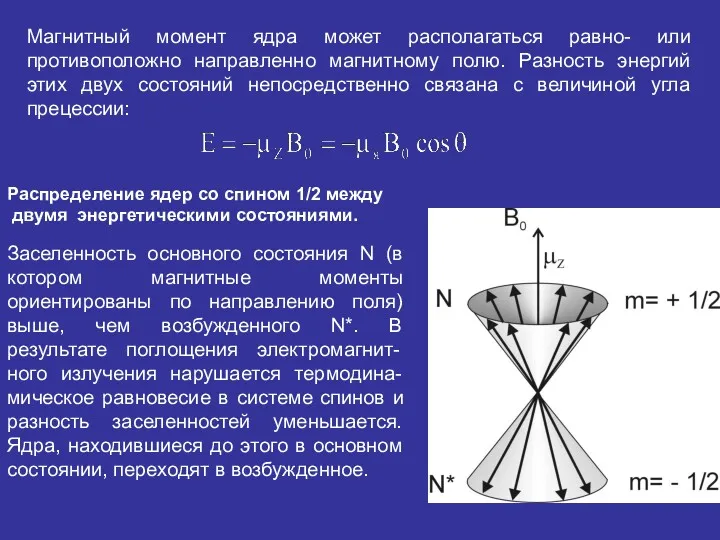
- 22. Магнитный момент ядра может располагаться равно- или противоположно направленно магнитному полю. Разность энергий этих двух состояний
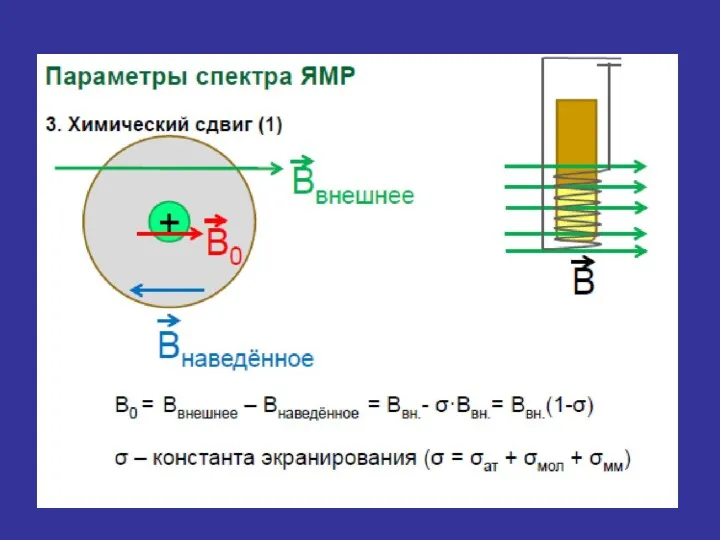
- 23. Поскольку резонансная частота ν0 и напряженность магнитного поля В0 взаимосвязаны через константу экранирования, то на практике
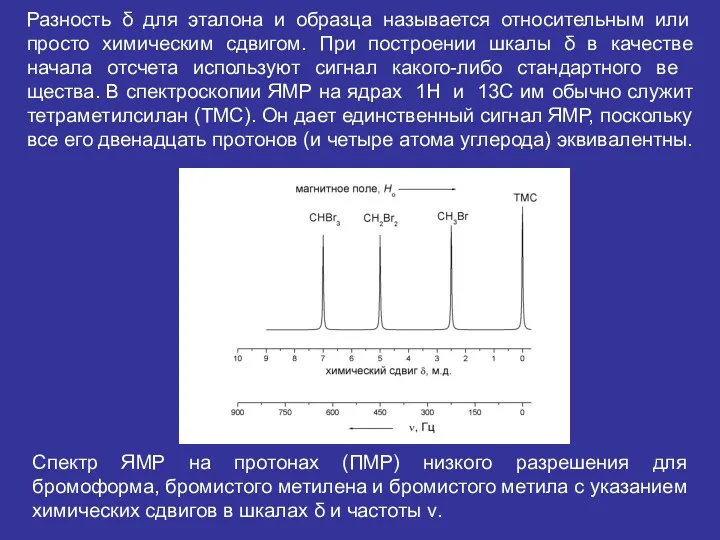
- 25. Разность δ для эталона и образца называется относительным или просто химическим сдвигом. При построении шкалы δ
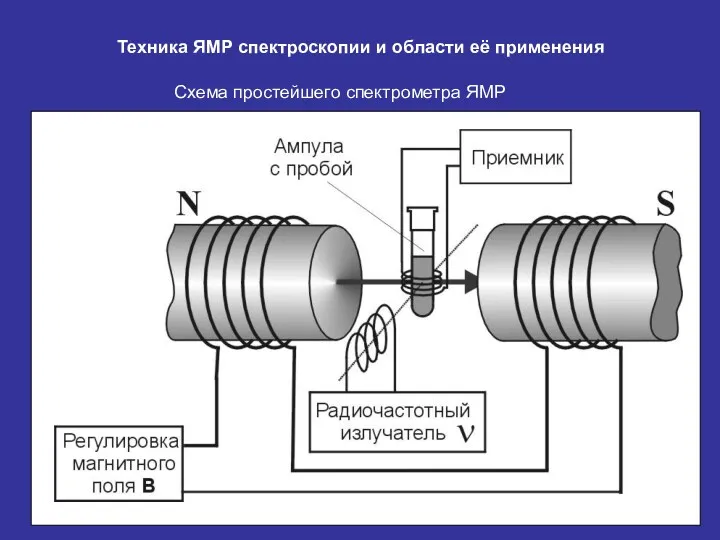
- 26. Техника ЯМР спектроскопии и области её применения Схема простейшего спектрометра ЯМР
- 27. Одни из первых спектрометров ЯМР фирмы Bruker Современный спектрометр ЯМР на электромагните Сканирующая ЯМР- спектроскопия
- 28. Современный приборы. Топ-модели. Магнит спектрометра ЯМР на 1000 МГц Bruker Германия Магнит спектрометра ЯМР на 900
- 29. Фурье–ЯМР-спектрометр Bruker Avance III 500 Год запуска: 2009 Современный приборы. Средний класс.
- 30. Фурье–ЯМР-спектрометр Bruker DPX 250 после upgrade 'a Год запуска: 1998. Современный приборы. Средний класс.
- 31. Жидкостный хроматограф в комплексе с ЯМР-спектрометром Физико-химические комплексы
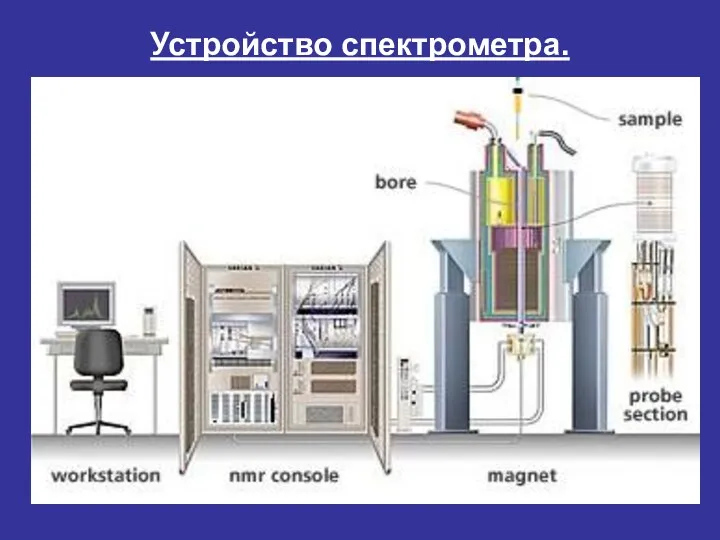
- 32. Устройство спектрометра.
- 33. Устройство спектрометра. Магнит
- 34. Устройство спектрометра. Магнит
- 35. Устройство спектрометра. Ампулы Набор для пробоподготовки для твердотельного датчика: - воронка - ампула - крышка -экстрактор
- 36. Пробоподготовка.
- 37. Пробоподготовка. Чистая ампула - Однородный раствор - Объем раствора (15-17 мм) - Плотно надетый колпачок
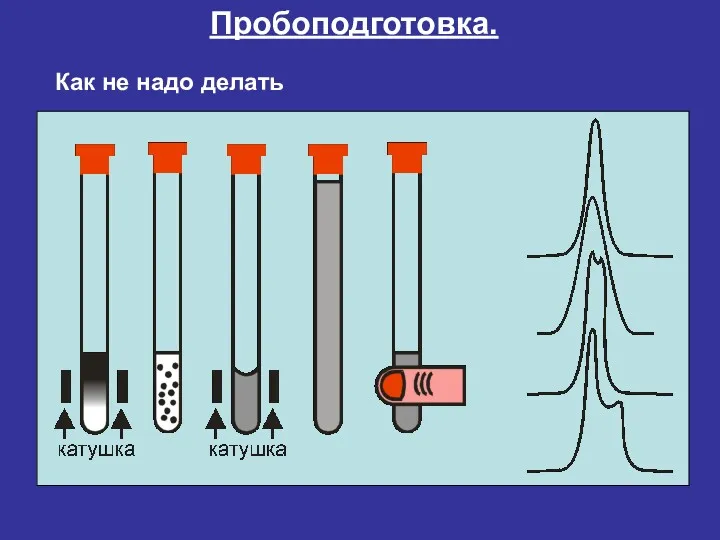
- 38. Пробоподготовка. Как не надо делать
- 39. Современный приборы. Средний класс Фурье ЯМР-спектрометр Bruker AM-400 под управлением Aspect 3000. Фурье ЯМР-спектрометр Bruker AС-200
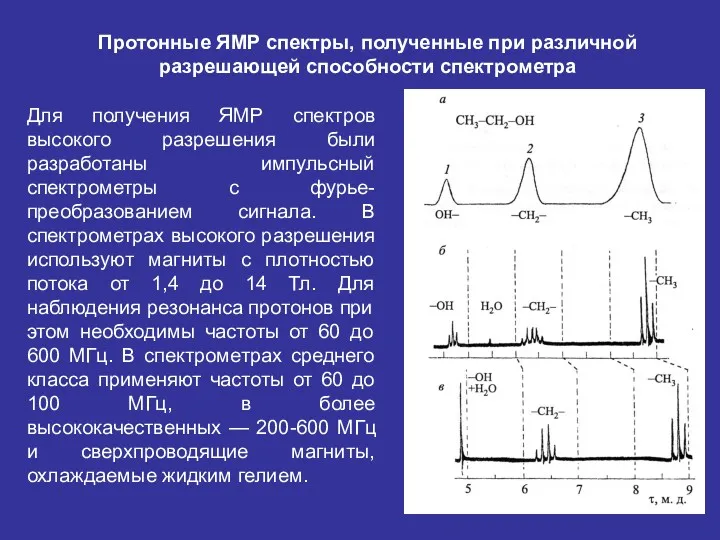
- 40. Протонные ЯМР спектры, полученные при различной разрешающей способности спектрометра Для получения ЯМР спектров высокого разрешения были
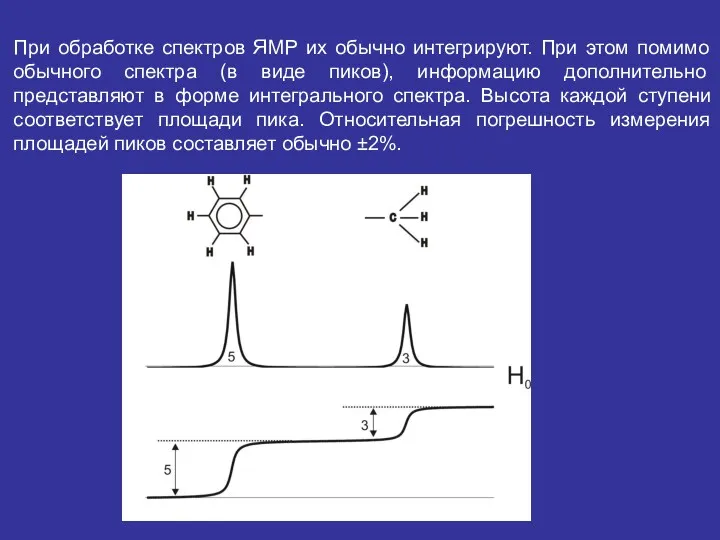
- 41. При обработке спектров ЯМР их обычно интегрируют. При этом помимо обычного спектра (в виде пиков), информацию
- 44. Скачать презентацию




























 Физические методы измерений. Виды и методы измерений. (Лекция 1)
Физические методы измерений. Виды и методы измерений. (Лекция 1) Органические полупроводники
Органические полупроводники урок по физике в 10 классе Силы трения с презентацией
урок по физике в 10 классе Силы трения с презентацией Графические физические задачи. Основные виды, этапы, решения
Графические физические задачи. Основные виды, этапы, решения Измерение атмосферного давления. К уроку по физике в 7 классе
Измерение атмосферного давления. К уроку по физике в 7 классе Пара сил и момент силы относительно точки
Пара сил и момент силы относительно точки Механика сплошных сред
Механика сплошных сред КРИСТАЛЛИЧЕСКИЕ ТЕЛА
КРИСТАЛЛИЧЕСКИЕ ТЕЛА Техника транспорта, обслуживание и ремонт. Ремонт кривошипно-шатунного механизма. (Тема 9.1)
Техника транспорта, обслуживание и ремонт. Ремонт кривошипно-шатунного механизма. (Тема 9.1) Система допусков и посадок ISO. Расчет и выбор посадок
Система допусков и посадок ISO. Расчет и выбор посадок Инструментальные методы анализа. Классификация методов
Инструментальные методы анализа. Классификация методов Плазма. Особенность
Плазма. Особенность Русские изобретения, без которых нельзя представить современный мир
Русские изобретения, без которых нельзя представить современный мир Магнитное поле постоянного электрического тока
Магнитное поле постоянного электрического тока How to use 5 service ports
How to use 5 service ports Зависимость силы тока от напряжения. Электрическое сопротивление
Зависимость силы тока от напряжения. Электрическое сопротивление Лекция 1. Экспериментальные методы физики твердого тела
Лекция 1. Экспериментальные методы физики твердого тела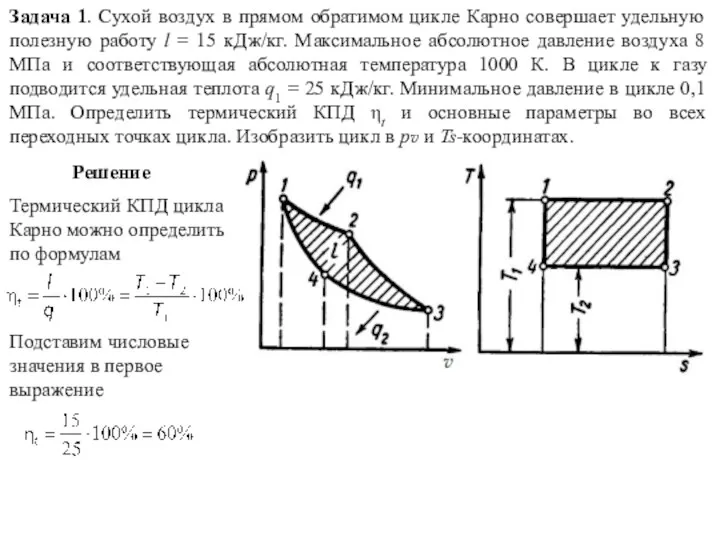 Задачи. Термодинамические циклы
Задачи. Термодинамические циклы Траектория движение тела, брошенного под углом к горизонту, с учетом сопротивления ветра
Траектория движение тела, брошенного под углом к горизонту, с учетом сопротивления ветра Методы испытаний ГТД и СУ. Лекция 1,2
Методы испытаний ГТД и СУ. Лекция 1,2 Презентация по теме Излучения и спектры 11 класс
Презентация по теме Излучения и спектры 11 класс Подшипники скольжения
Подшипники скольжения Способы герметизации клепаных швов и изделий
Способы герметизации клепаных швов и изделий Агрегатные состояния вещества. Плавление и отвердевание кристаллических тел
Агрегатные состояния вещества. Плавление и отвердевание кристаллических тел Ускорение свободного падения на других планетах
Ускорение свободного падения на других планетах Электрический ток
Электрический ток Атомный реактор
Атомный реактор Насыщенный пар
Насыщенный пар