Содержание
- 2. Математики видят ее в: гармонии чисел и форм, геометрической выразительности, стройности математических формул, решении задач различными
- 3. Но красота математики выражается не только в красоте форм ,наглядной выразительности математических объектов, восприятие которых сопряжено
- 4. Можно ли насладиться решением уравнения sinx-cosx=1? Да, если стать его исследователем! способы решения уравнения sinx-cosx=1 и
- 5. Универсальные методы решения уравнения sin x – cos x=1 Мы уже говорили о богатстве приложений универсальных
- 6. Мы не просто в правой части уравнения получили ноль,мы выделили выражение 1 + cos x …
- 7. Ну, конечно,вы догадались ! Необходимо перейти к половинному аргументу, применив формулу повышения степени и формулу двойного
- 8. Разложение левой части уравнения на множители sinx-cosx=1 1-й способ
- 9. Произведение равное нулю, если хотя бы один из множителей равен нулю, а остальные при этом не
- 10. Делим обе его части на что противоречит тождеству Получим Ответ:
- 11. А может вы заметили, что левая часть уравнения sin x – cos x является однородным выражением
- 12. Приведение уравнения к однородному относительно синуса и косинуса sinx-cosx=1 Разложим левую часть по формулам двойного аргумента,
- 13. Тригонометрия удивительна тем ,что она даёт собственные оригинальные способы преобразования разности (или суммы) тригонометрических функций в
- 14. 3-й способ. Преобразование разности ( или суммы) тригонометрических функций в произведение. sinx-cosx=1 Запишем уравнение в виде:
- 15. Другим универсальным методом решения уравнений является замена переменной. И хотя для данного уравнения этот способ не
- 16. 4-й способ Приведение к квадратному уравнению относительно одной из функций sinx-cosx=1 Так как Возведем обе части
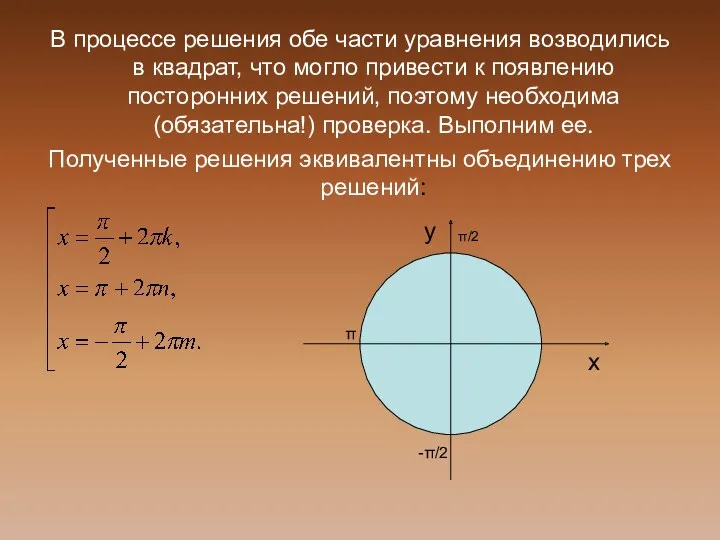
- 17. В процессе решения обе части уравнения возводились в квадрат, что могло привести к появлению посторонних решений,
- 18. Первое и второе решения совпадают с ранее полученными, поэтому не являются посторонними. Проверим Левая часть: Правая
- 19. 5-й способ Выражение всех функций через tgx (универсальная подстановка) по формулам: С учетом приведенных формул уравнение
- 20. Умножим обе части уравнения на ОДЗ первоначального уравнения – все множество R.
- 21. При переходе к из рассмотрения выпали значения, при которых не имеет смысла, т.е. Следует проверить, не
- 22. На ряду с универсальными методами решения уравнений, есть и специфические. Наиболее ярким из них является метод
- 23. 6-й способ Введение вспомогательного угла (числа) sinx-cosx=1 В левой части вынесем за скобку ( корень квадратный
- 24. С помощью тригонометрического круга легко установить, что решение распадается на два случая х у π/4 3π/4
- 25. 7-способ Возведение обеих частей уравнения в квадрат sinx-cosx=1
- 26. Полученное решение эквивалентно объединению четырех решений: Проверка показывает, что первое и четвертое решения – посторонние. Ответ:
- 28. Скачать презентацию
























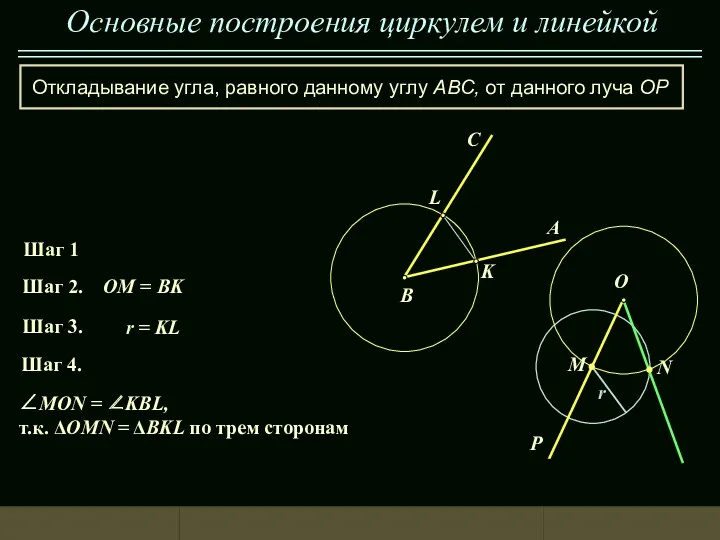 Построение угла равного данному
Построение угла равного данному Треугольник
Треугольник Конспект урока Взаимное расположение прямой и окружности Геометрия 8 класс
Конспект урока Взаимное расположение прямой и окружности Геометрия 8 класс Математические термины
Математические термины Три точки зрения на геометрию вселенной
Три точки зрения на геометрию вселенной треугольники и их виды
треугольники и их виды построение сечений
построение сечений Интерактивный плакат по геометрии Признаки равенства треугольников 7 класс
Интерактивный плакат по геометрии Признаки равенства треугольников 7 класс Презентация к уроку геометрии Симметрия. Осевая симметрия.
Презентация к уроку геометрии Симметрия. Осевая симметрия. урок-презентация Цилиндр
урок-презентация Цилиндр Урок объяснения нового материала по геометрии в 10 классе. Тема: Параллельность прямой и плоскости
Урок объяснения нового материала по геометрии в 10 классе. Тема: Параллельность прямой и плоскости задачи на готовых чертежах по теме: Ромб
задачи на готовых чертежах по теме: Ромб Осевая симметрия
Осевая симметрия 7класс Геометрия Перпендикулярные прямые
7класс Геометрия Перпендикулярные прямые Сумма углов треугольника
Сумма углов треугольника Презентация к уроку Пропорциональные отрезки в прямоугольном треугольнике
Презентация к уроку Пропорциональные отрезки в прямоугольном треугольнике Пирамида
Пирамида Урок геометрии в 8 классе Свойства трапеции
Урок геометрии в 8 классе Свойства трапеции Первый признак равенства треугольников
Первый признак равенства треугольников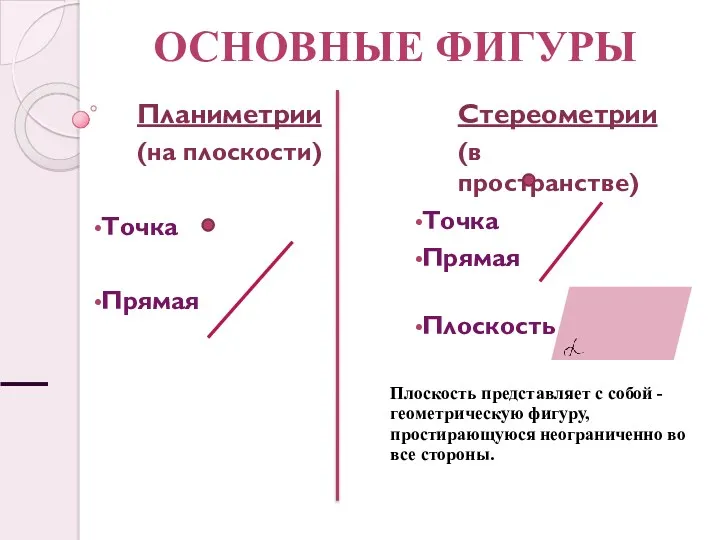 Основные понятия стереометрии
Основные понятия стереометрии урок геометрии в 8 классе Иследование некоторых фактов из геометрии четырехугольников
урок геометрии в 8 классе Иследование некоторых фактов из геометрии четырехугольников Простейшие задачи в координатах
Простейшие задачи в координатах Презентация элективного курса по геометрии. 10 класс.
Презентация элективного курса по геометрии. 10 класс. Бинарный урок по геометрии и информатике Параллелограмм и трапеция
Бинарный урок по геометрии и информатике Параллелограмм и трапеция Сборник УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ Смежные и вертикальные углы
Сборник УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ Смежные и вертикальные углы тест по геометрии 7 класс
тест по геометрии 7 класс Тема ШАР
Тема ШАР Признаки параллельности двух прямых на плоскости
Признаки параллельности двух прямых на плоскости