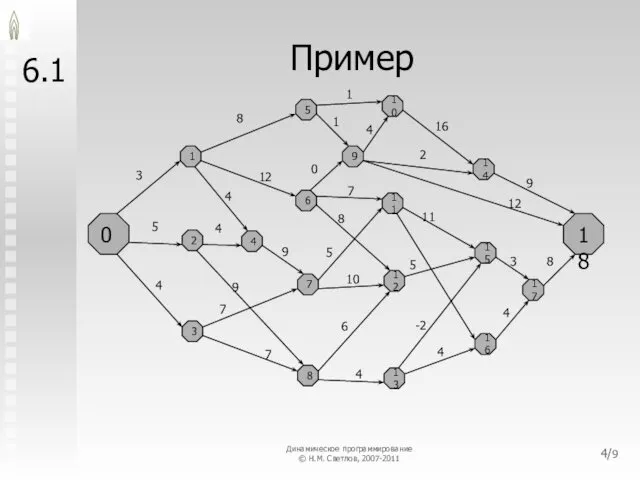
Математическая запись
6.1
/9
1, если путь проходит через дугу (i,j)
0, если не
проходит или такой дуги нет
Например, расстояние между пунктами i и j, км
{(1,2), (1,3), (2,4), (2,5), (3,5)…}
единственность искомого пути: в каждую вершину можно прийти только из одной вершины (или вообще нельзя)
если искомый путь пришёл в вершинуk, то он должен из неё выйти (если только она не конечная)
Условие целочисленности переменных
Между вершинами i и j нет дуги.
сумма числовых значений (e.g. расстояний) по всему пути
Динамическое программирование
© Н.М. Светлов, 2007-2011




 Пособие по плаванию в сети Интернет (родителям)
Пособие по плаванию в сети Интернет (родителям) Методы представления графических изображений
Методы представления графических изображений Android компоненттері
Android компоненттері Ввод изображения
Ввод изображения ОБЪЕКТ И ЕГО ХАРАКТЕРИСТИКА
ОБЪЕКТ И ЕГО ХАРАКТЕРИСТИКА Как заработать 150 000 рублей за месяц на одном товаре
Как заработать 150 000 рублей за месяц на одном товаре HTML құжатында кестелерді қалыптастыру. Кесте параметрлерін тағайындау тегтері
HTML құжатында кестелерді қалыптастыру. Кесте параметрлерін тағайындау тегтері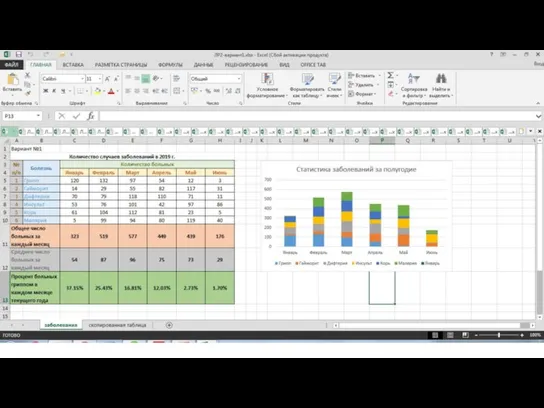 Заполнить таблицу
Заполнить таблицу Информационная система автоматизации обработки информации о реабилитации больных на санаторном этапе
Информационная система автоматизации обработки информации о реабилитации больных на санаторном этапе Changes in society by computing technology
Changes in society by computing technology Назначение и устройство компьютера. Компьютерная память.
Назначение и устройство компьютера. Компьютерная память. Обобщенная линейная модель множественной регрессии с гетероскедастичными остатками. Лекция 8
Обобщенная линейная модель множественной регрессии с гетероскедастичными остатками. Лекция 8 Приятные новости. Hot Talk представляет
Приятные новости. Hot Talk представляет Обработка информации. Информация и информационные процессы
Обработка информации. Информация и информационные процессы Операции и выражения. (Лекция 4)
Операции и выражения. (Лекция 4) Графический редактор Paint
Графический редактор Paint Итоги петровских преобразований. Урок по истории России в 10 класс. Интегрированный урок история + информатика
Итоги петровских преобразований. Урок по истории России в 10 класс. Интегрированный урок история + информатика Связи между классами. Объектно-ориентированное программирование. (Лекция 3)
Связи между классами. Объектно-ориентированное программирование. (Лекция 3) Корпоративные информационные системы
Корпоративные информационные системы Искусственный интеллект
Искусственный интеллект Поколения ЭВМ
Поколения ЭВМ Модуль управления движением автомобиля для системы оценки профессиональной пригодности водителей автотранспорта
Модуль управления движением автомобиля для системы оценки профессиональной пригодности водителей автотранспорта Работа с донорами. Письма донорам: технология и содержание
Работа с донорами. Письма донорам: технология и содержание Mathcad 2000 Professional
Mathcad 2000 Professional Алгоритмы и структуры данных. Алгоритмы сортировки
Алгоритмы и структуры данных. Алгоритмы сортировки Команда и программа
Команда и программа Системы автоматизации управления проектами
Системы автоматизации управления проектами 6 кроків для створення власного логотипу
6 кроків для створення власного логотипу