Содержание
- 2. І.Пошук в глибину
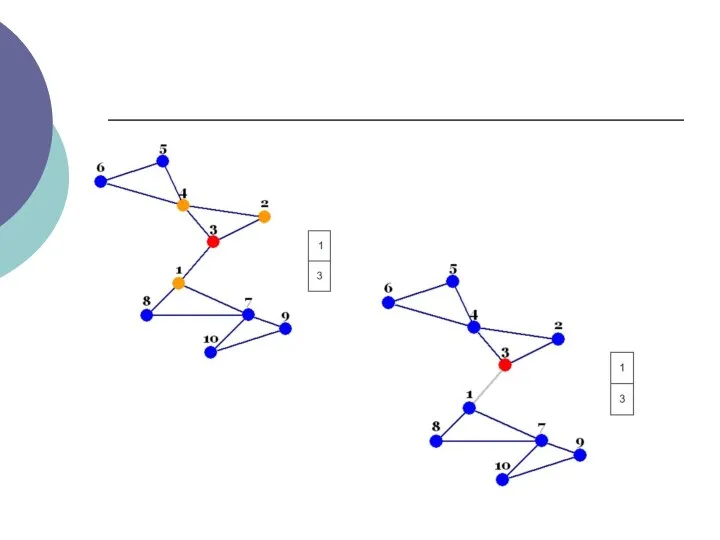
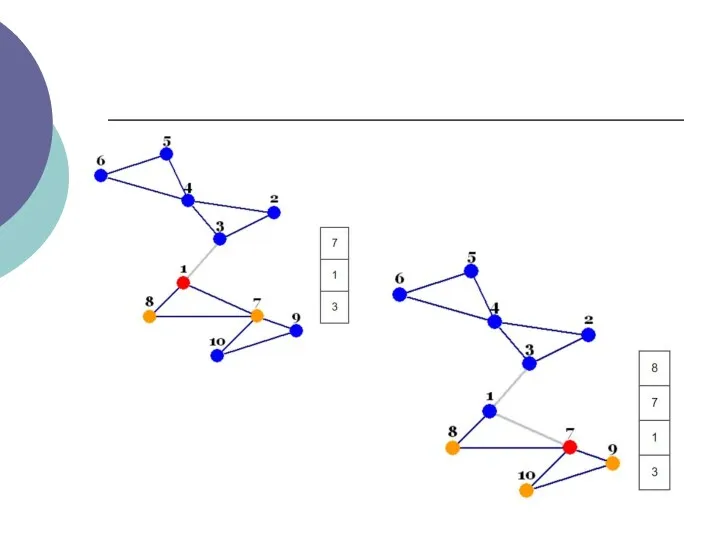
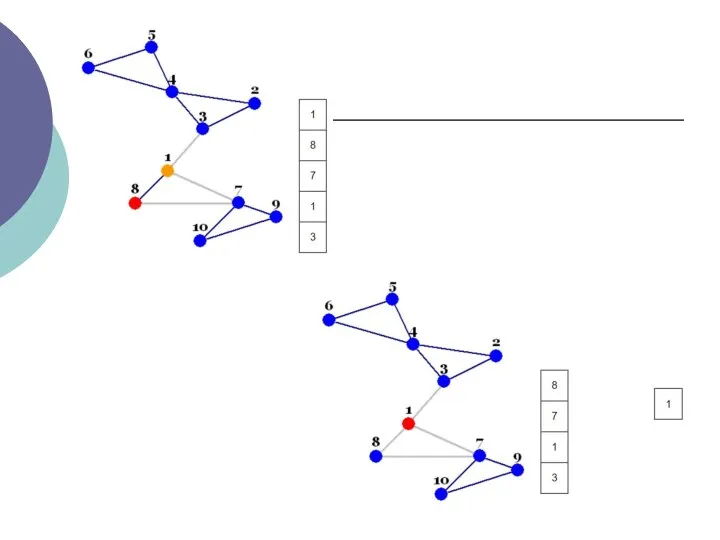
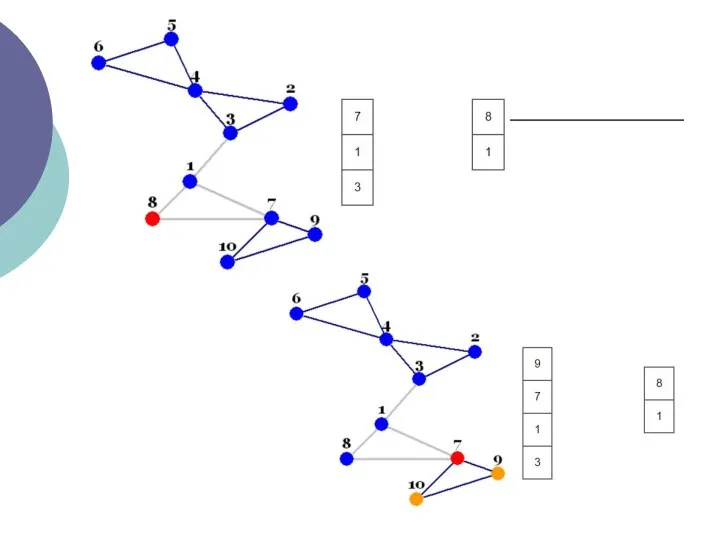
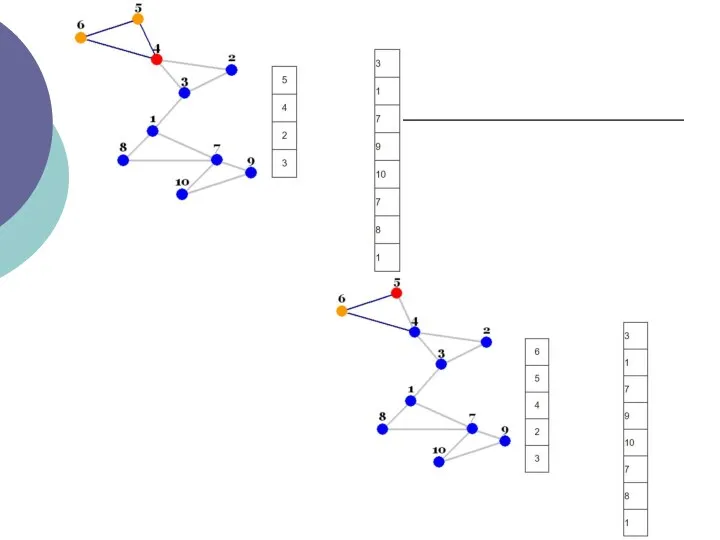
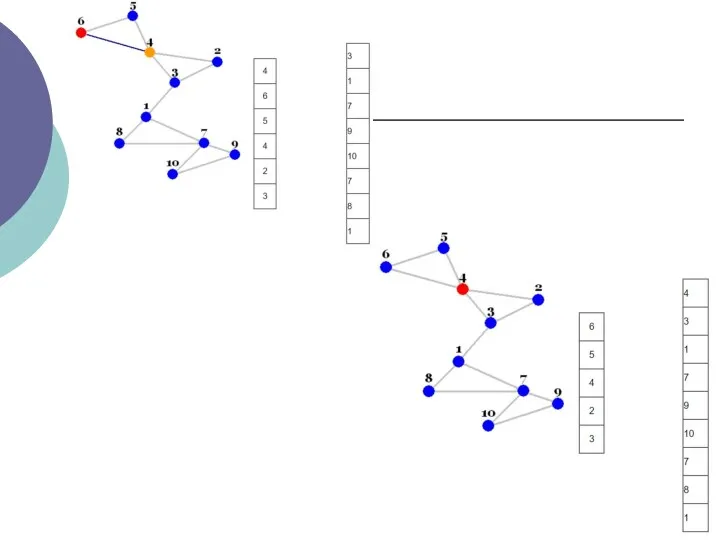
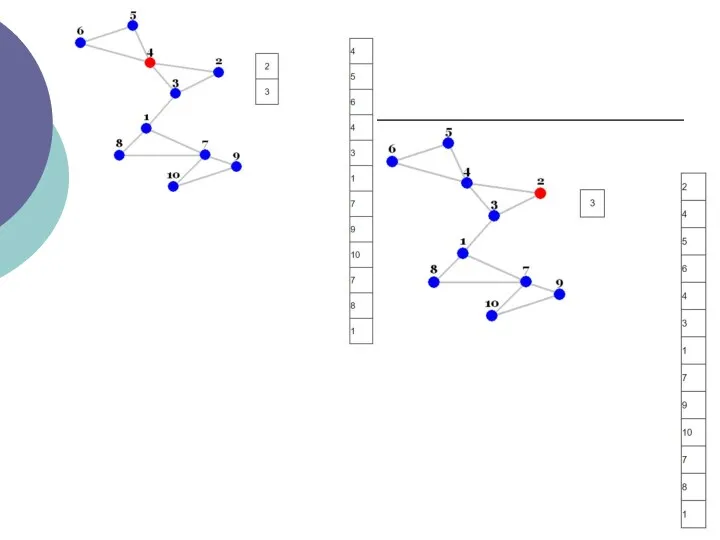
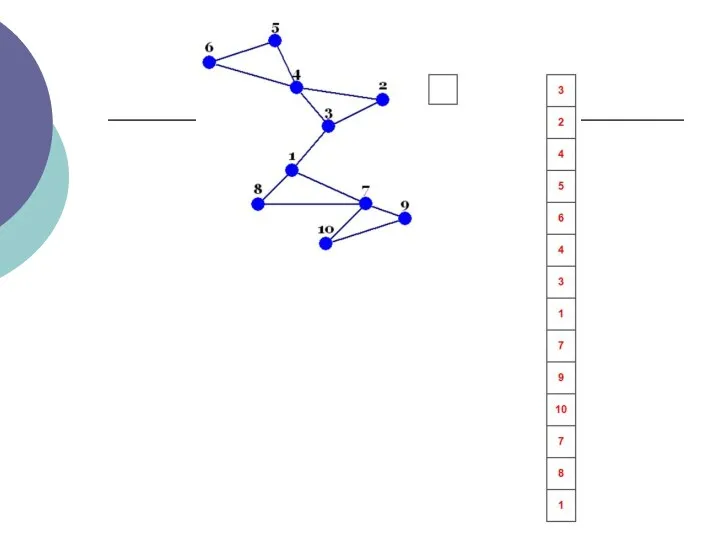
- 3. Пошук в глибину - це алгоритм обходу вершин графа. Пошук в ширину проводиться симетрично (вершини графа
- 4. Відсутність останнього свідчить про одну з двох можливих ситуацій: всі вершини графа вже переглянуті, переглянуті вершини
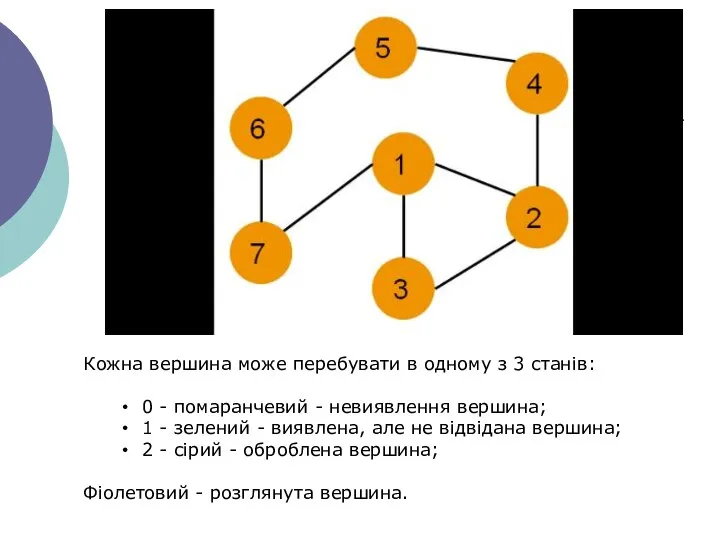
- 5. Кожна вершина може перебувати в одному з 3 станів: 0 - помаранчевий - невиявлення вершина; 1
- 6. #include using namespace std; int mas[7][7] = { { 0, 1, 1, 0, 0, 0, 1
- 7. void search(int st, int n) { int r; cout
- 9. #include #include // стек using namespace std; struct Edge { int begin; int end; }; int
- 10. cout > req; req--; Stack.push(0); // заносимо в стек першу вершину while (!Stack.empty()){ // поки стек
- 11. cout
- 12. Пошук будь-якого шляху в графі. Пошук лексикографічно першого шляху в графі. Перевірка, чи є одна вершина
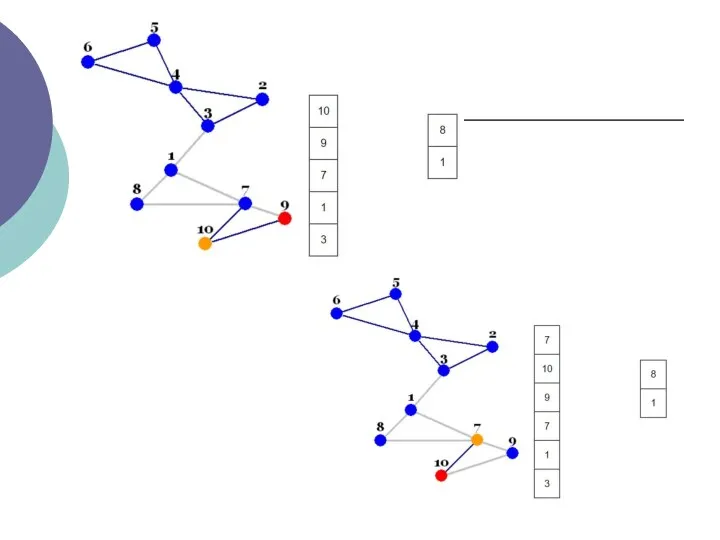
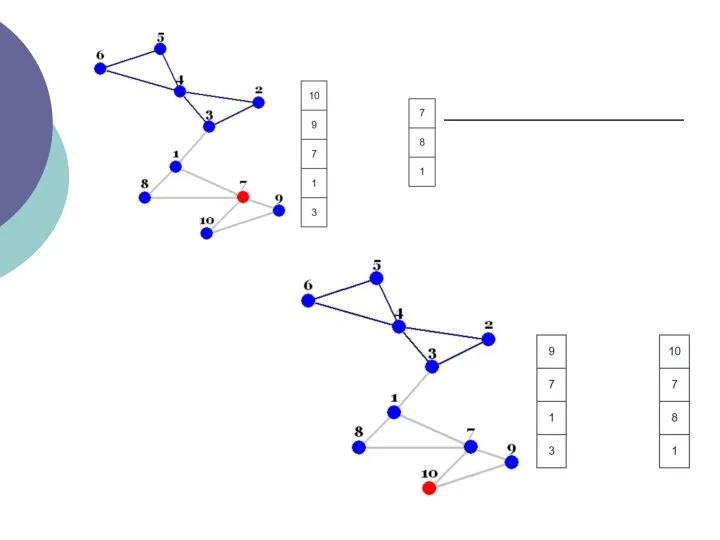
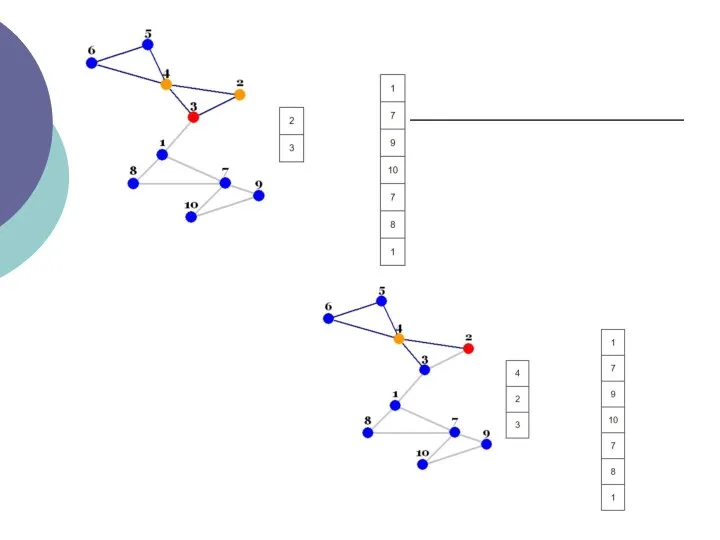
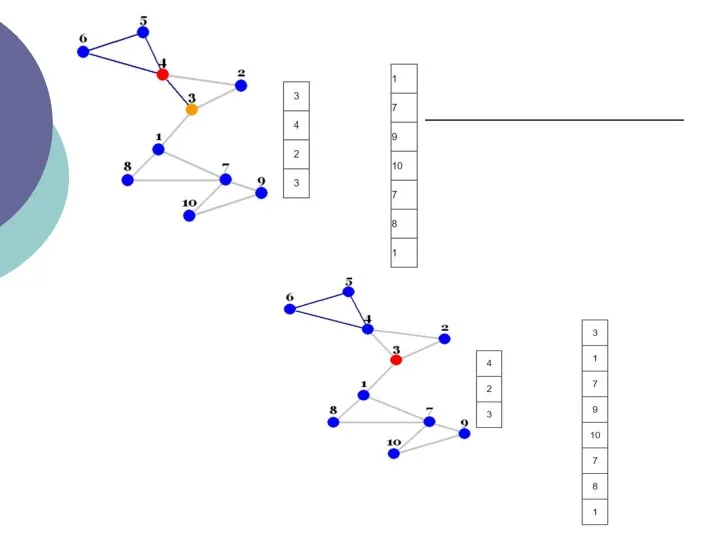
- 13. ІІ.Алгоритм Дейкстри
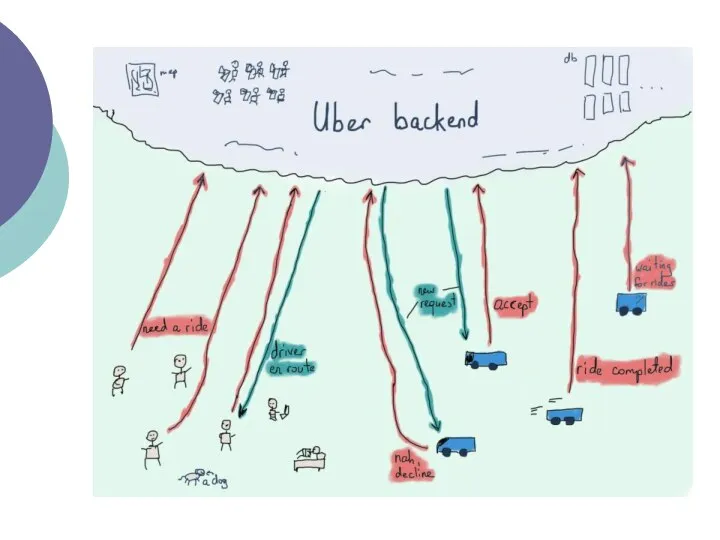
- 14. З його 50 мільйонами користувачів і 7 мільйонами водіїв (джерело), одна з найважливіших речей, яка має
- 16. Крім обробки вхідних запитів і знаходження області розташування на основі координат користувача, а потім знаходження водіїв
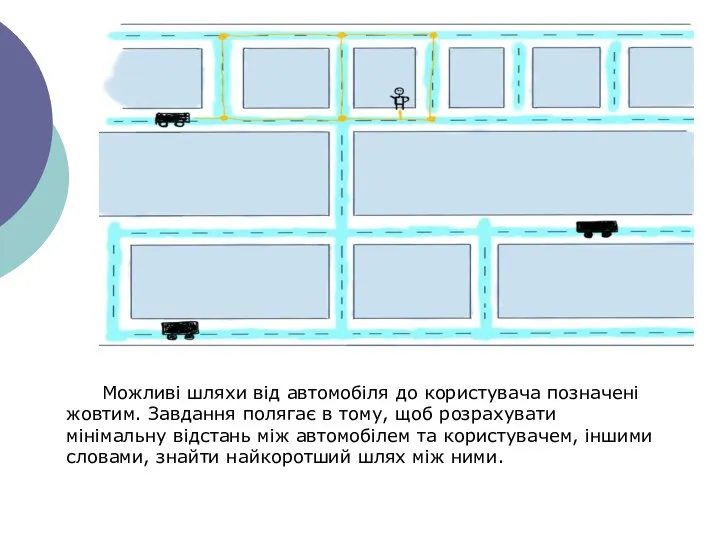
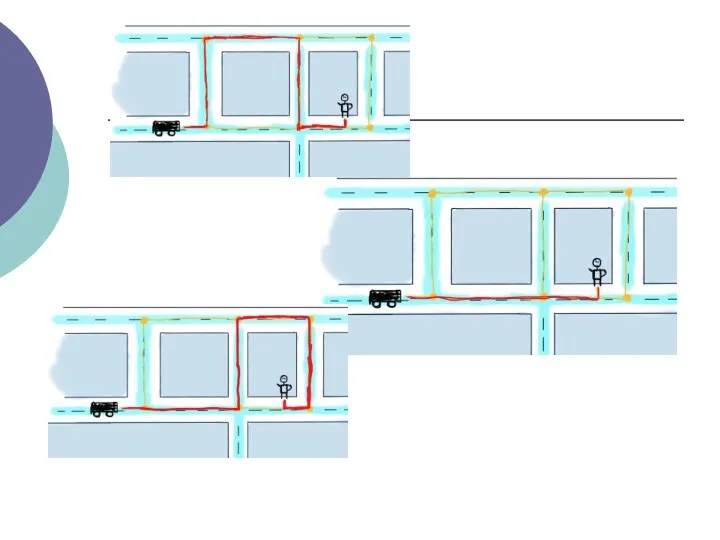
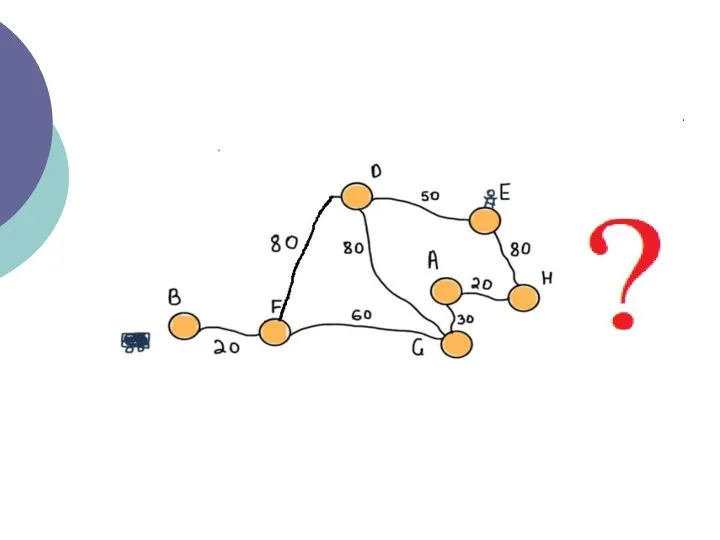
- 17. Можливі шляхи від автомобіля до користувача позначені жовтим. Завдання полягає в тому, щоб розрахувати мінімальну відстань
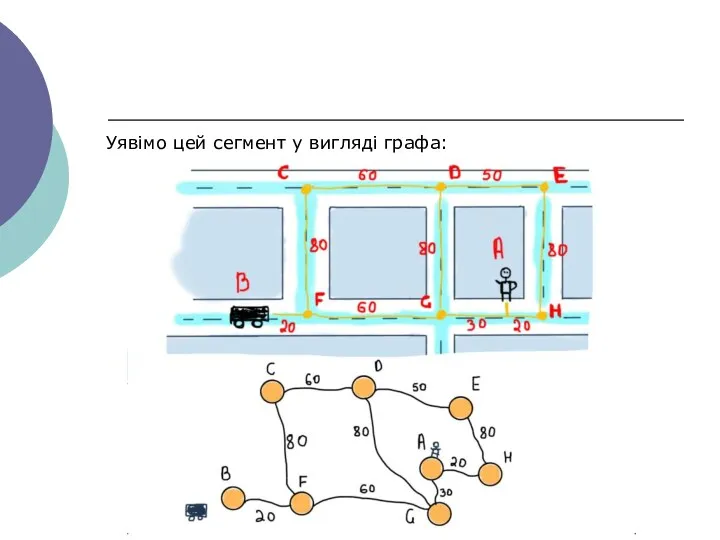
- 19. Уявімо цей сегмент у вигляді графа:
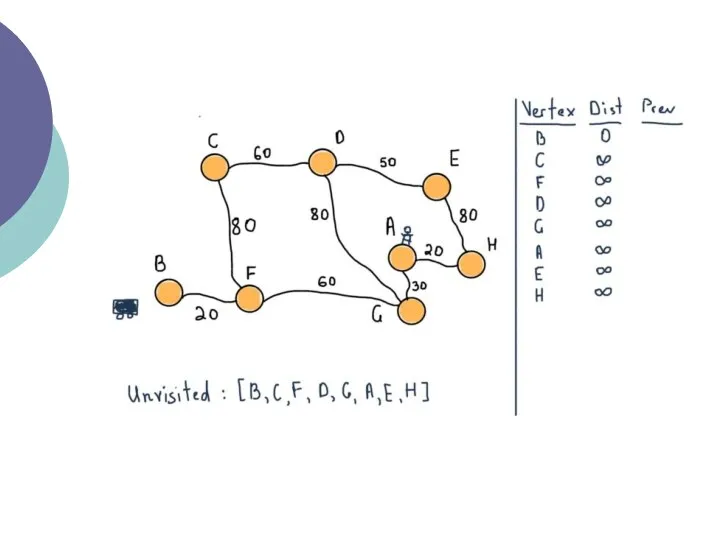
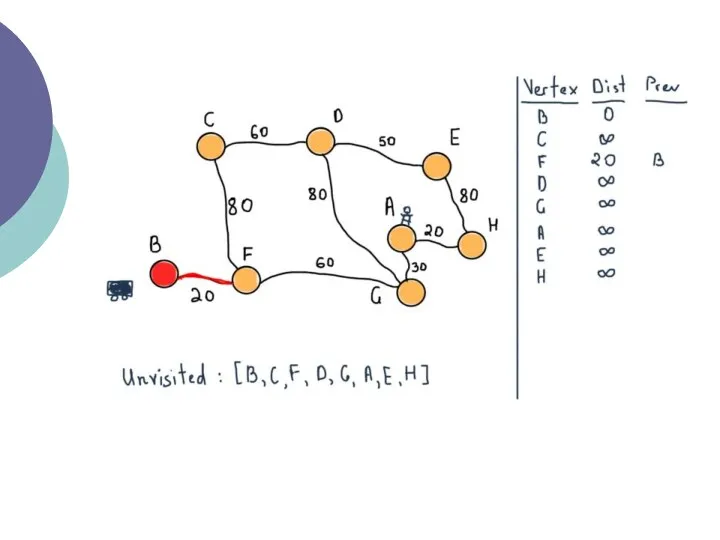
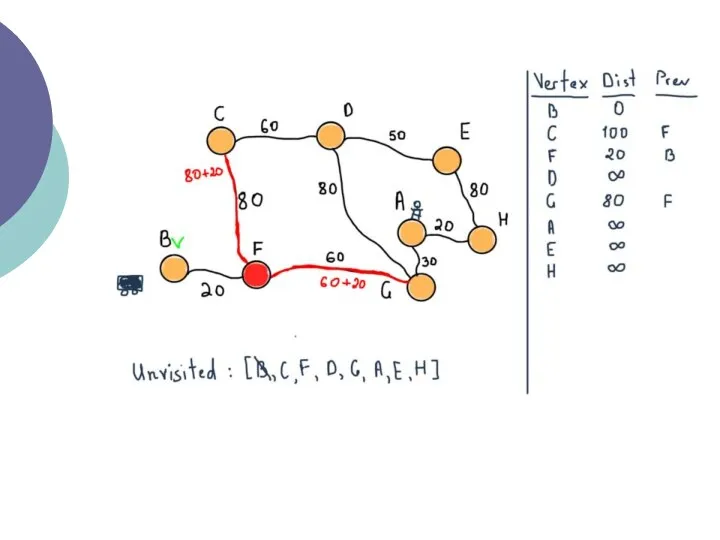
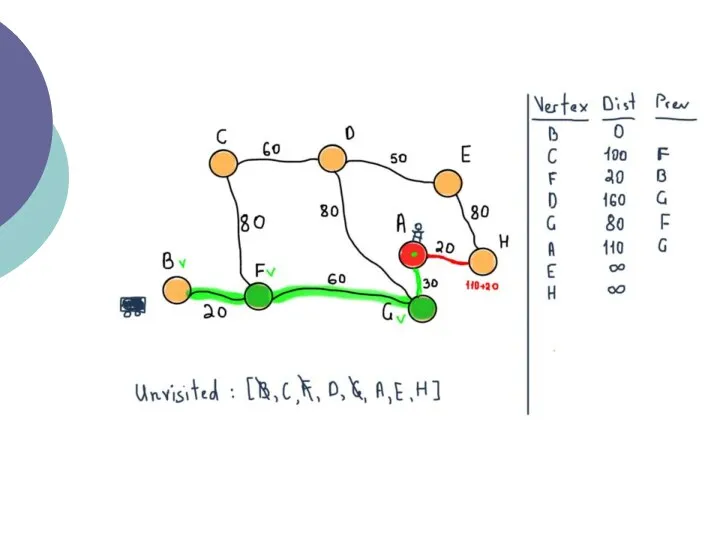
- 20. Відзначте всі вершини як ще невідвідані. Створіть структуру всіх невідвіданих вершин. Дайте кожній вершині значення відстань
- 21. Коли ми закінчимо розглядати всіх сусідів поточної вершини, відзначте поточну вершину як відвідану і видаліть її
- 28. Програмна реалізація #include #include #define SIZE 6 int main(){ int a[SIZE][SIZE]; // матриця суміжності int d[SIZE];
- 29. for (int i = 0; i
- 30. // Додаємо знайдену мінімальну вагу до поточної ваги вершини // і порівнюємо з поточною мінімальною вагою
- 31. ІІІ.Алгоритм Флойда-Уоршелла
- 32. Алгоритм Флойда-Воршелла використовується для розв'язання задачі про найкоротший шлях у зваженому графі з додатними або від'ємними
- 33. Алгоритм Воршелла порівнює всі можливі шляхи в графі між кожною парою вершин. Він виконується за Θ(|V|³)
- 34. Розгляньмо граф G з ребрами V, пронумерованими від 1 до N. Крім того розгляньмо функцію shortestPath(i,
- 35. Для кожної з цих пар вершин, найкоротший шлях може бути або (1)- шлях, у якому є
- 36. Ця формула є основною частиною алгоритму Флойда-Воршелла. Алгоритм спочатку обчислює shortestPath(i, j, k) для всіх пар(i,
- 37. ІV. Ейлерів Граф
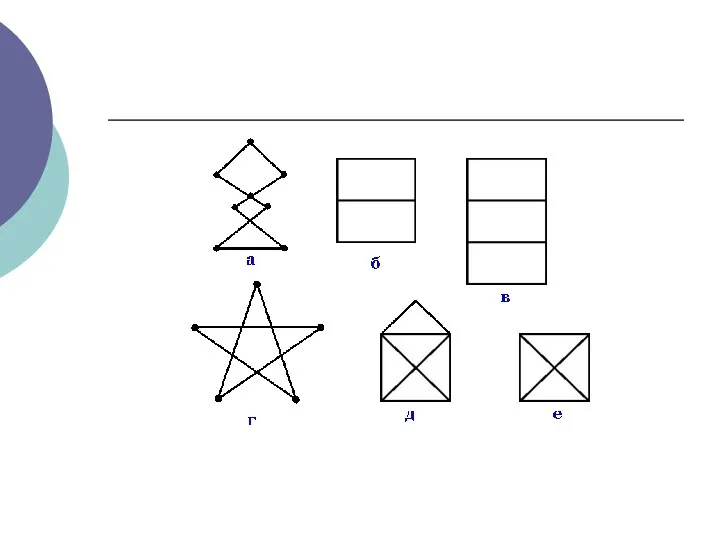
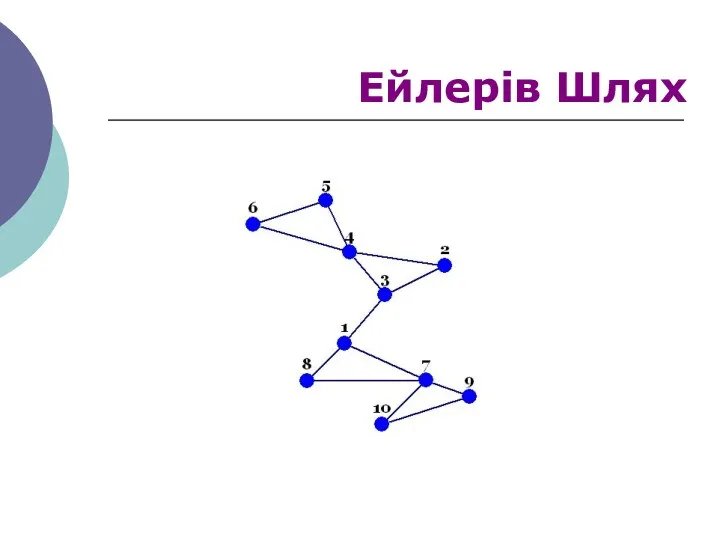
- 39. Ейлеревим шляхом у графі називається шлях, що містить всі ребра графа. Ейлеревим циклом у графі називається
- 40. Тв 1. Якщо граф має ейлерів цикл, то він зв'язний і всі його вершини парні. Справді,
- 41. Тв 3. Якщо граф містить ейлерів шлях з кінцями А та В (А не співпадає з
- 42. Тв 4. Якщо граф зв'язний та А і В єдині непарні вершини, то граф має ейлерів
- 43. Ейлерів Шлях
- 59. Дякую за увагу
- 62. Скачать презентацию



![#include using namespace std; int mas[7][7] = { { 0,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/580617/slide-5.jpg)































 Что такое socket.io
Что такое socket.io Object oriented programming. (Lesson 6, part 2)
Object oriented programming. (Lesson 6, part 2) Полезные адреса Интернет-ресурсов
Полезные адреса Интернет-ресурсов Аппаратное и программное обеспечение ЭВМ и сетей
Аппаратное и программное обеспечение ЭВМ и сетей Способы передачи движения. Модель: Мотоцикл с коляской. Занятие №4
Способы передачи движения. Модель: Мотоцикл с коляской. Занятие №4 Запоминающие устройства компьютера. (Лекция 5)
Запоминающие устройства компьютера. (Лекция 5) Значение логического выражения. Решение задания 3. ОГЭ
Значение логического выражения. Решение задания 3. ОГЭ Процесс загрузки и BIOS
Процесс загрузки и BIOS Электронная почта. Сетевое коллективное взаимодействие и сетевой этикет
Электронная почта. Сетевое коллективное взаимодействие и сетевой этикет Установка виртуальной машины. Установка операционной системы
Установка виртуальной машины. Установка операционной системы Управление файловой системой
Управление файловой системой Структуры данных
Структуры данных Условные операторы
Условные операторы Офіційний майданчик державних закупівель. Ваше зручне місце для торгів. Public-Bid
Офіційний майданчик державних закупівель. Ваше зручне місце для торгів. Public-Bid Введение в Matlab
Введение в Matlab Практическая работа в MS PowerPoint-2010
Практическая работа в MS PowerPoint-2010 Порядок оформления заказа
Порядок оформления заказа Я и интернет будущего
Я и интернет будущего Виды компьютерных сетей
Виды компьютерных сетей Принципы построения компьютеров
Принципы построения компьютеров Способы адресации в микропроцессорных системах
Способы адресации в микропроцессорных системах Оценка сложности вычислительных алгоритмов. Лекция 22
Оценка сложности вычислительных алгоритмов. Лекция 22 Парадигмы программирования
Парадигмы программирования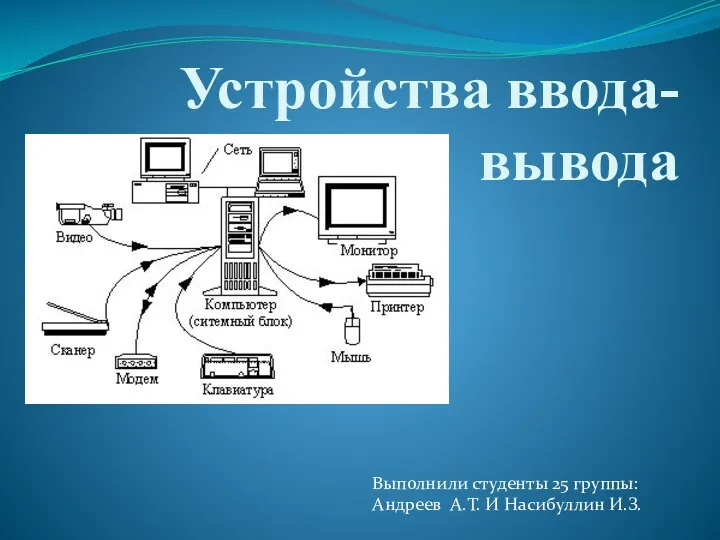 Устройства ввода-вывода
Устройства ввода-вывода Презентация к уроку информатики и ИКТ
Презентация к уроку информатики и ИКТ Создание графических изображений. Обработка графической информации. Информатика. 7 класс
Создание графических изображений. Обработка графической информации. Информатика. 7 класс Всероссийская перепись населения 2020
Всероссийская перепись населения 2020 презентация электронного учебника
презентация электронного учебника