Содержание
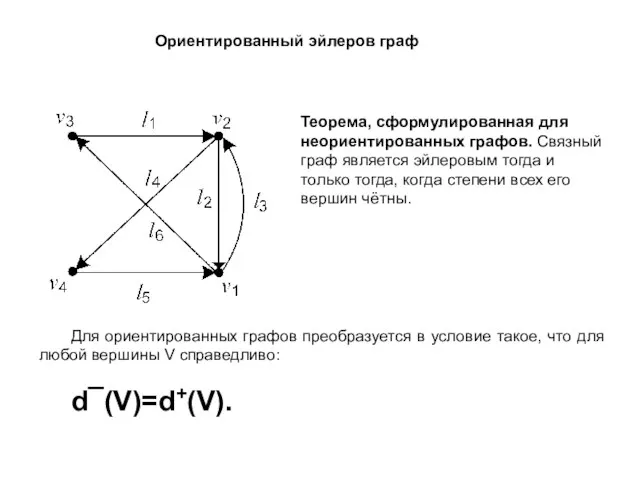
- 2. Ориентированный эйлеров граф Теорема, сформулированная для неориентированных графов. Связный граф является эйлеровым тогда и только тогда,
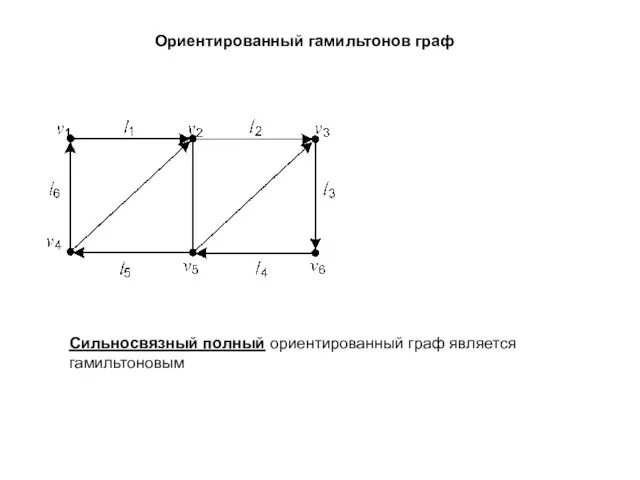
- 3. Ориентированный гамильтонов граф Сильносвязный полный ориентированный граф является гамильтоновым
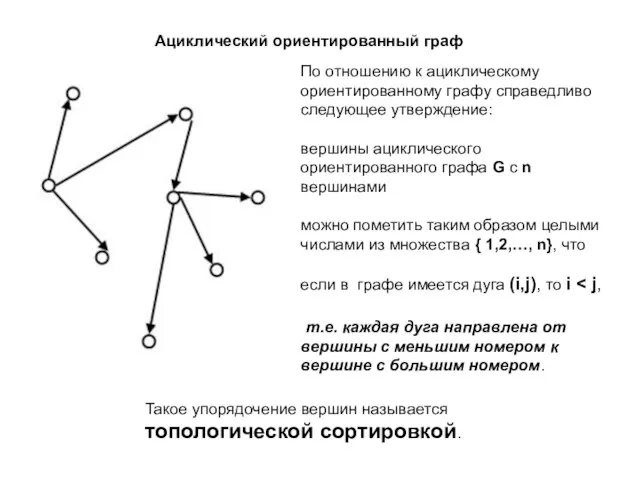
- 4. Ациклический ориентированный граф По отношению к ациклическому ориентированному графу справедливо следующее утверждение: вершины ациклического ориентированного графа
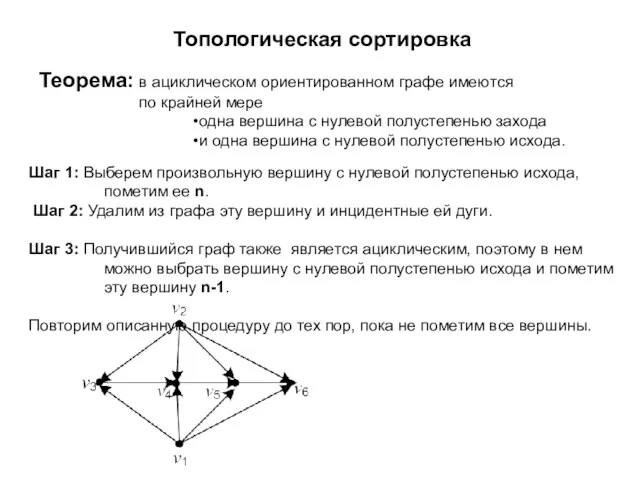
- 5. Топологическая сортировка Теорема: в ациклическом ориентированном графе имеются по крайней мере одна вершина с нулевой полустепенью
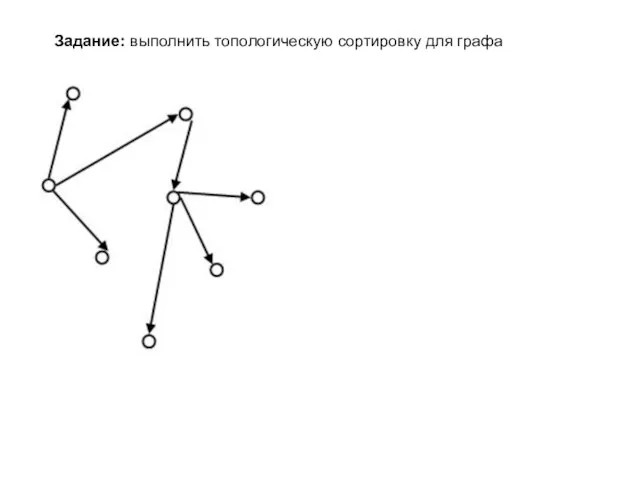
- 6. Задание: выполнить топологическую сортировку для графа
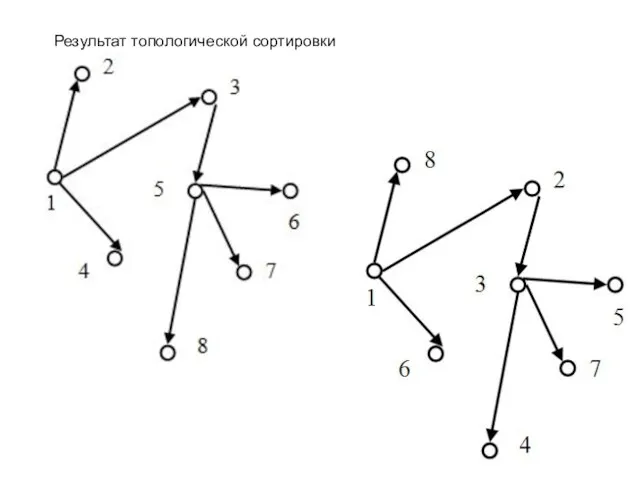
- 7. Результат топологической сортировки
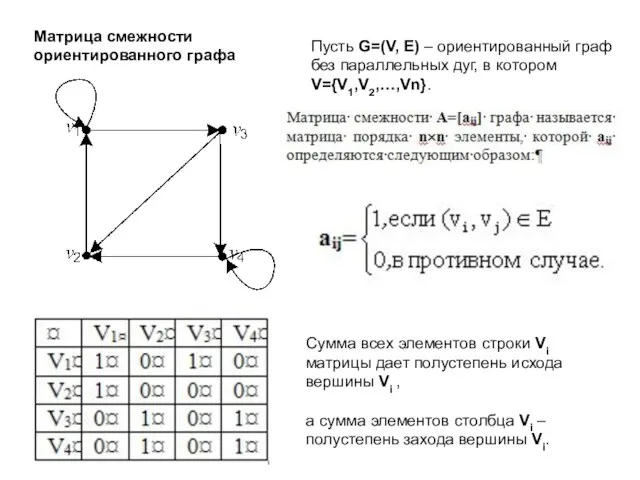
- 8. Матрица смежности ориентированного графа Пусть G=(V, E) – ориентированный граф без параллельных дуг, в котором V={V1,V2,…,Vn}.
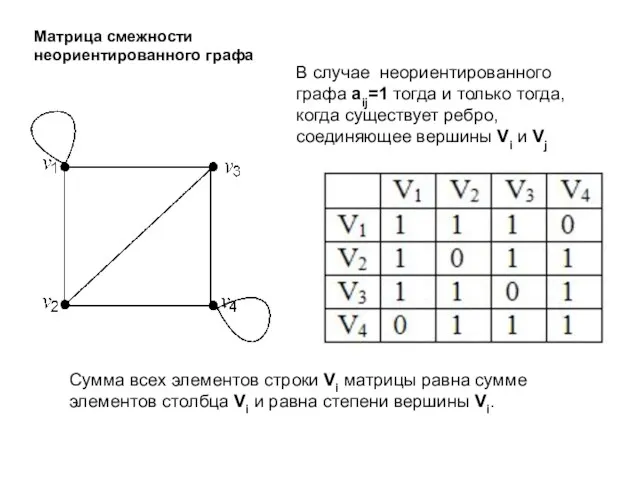
- 9. Матрица смежности неориентированного графа В случае неориентированного графа aij=1 тогда и только тогда, когда существует ребро,
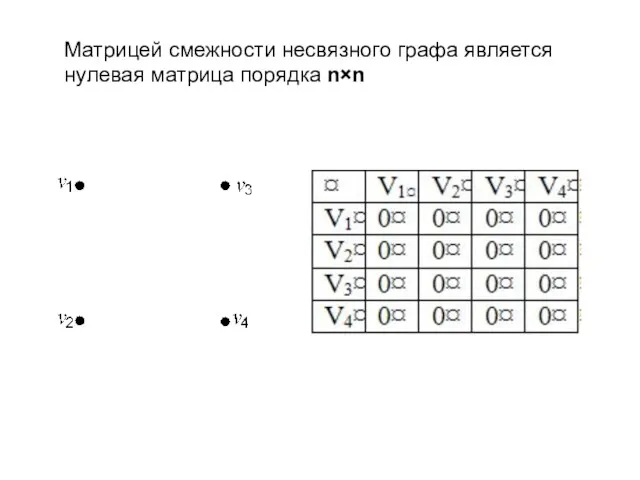
- 10. Матрицей смежности несвязного графа является нулевая матрица порядка n×n
- 11. Матрица достижимостей R=[rij] Все диагональные элементы в матрице R равны 1, поскольку каждая вершина достижима из
- 12. Вопрос 1. Как будет выглядеть матрица достижимости для неоринтированного графа? Вопрос 2. Как будет выглядеть матрица
- 13. Матрица инциденций B=[bij] Если граф G ориентированный Если граф G неориентированный Рассмотрим граф G на n
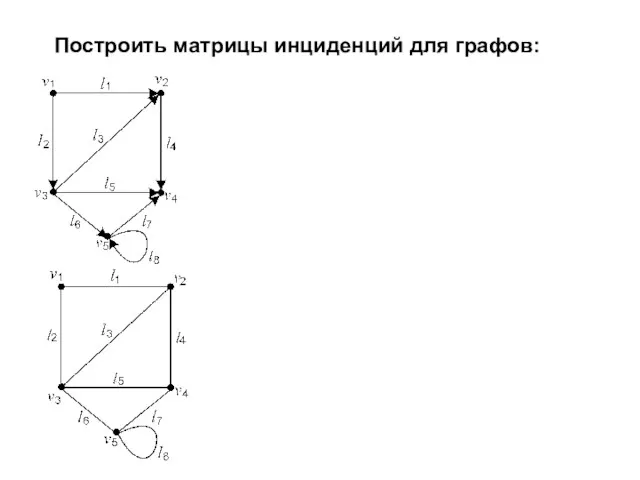
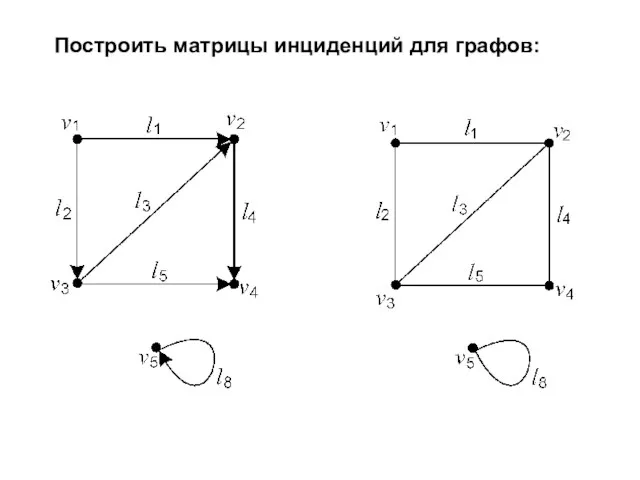
- 14. Построить матрицы инциденций для графов:
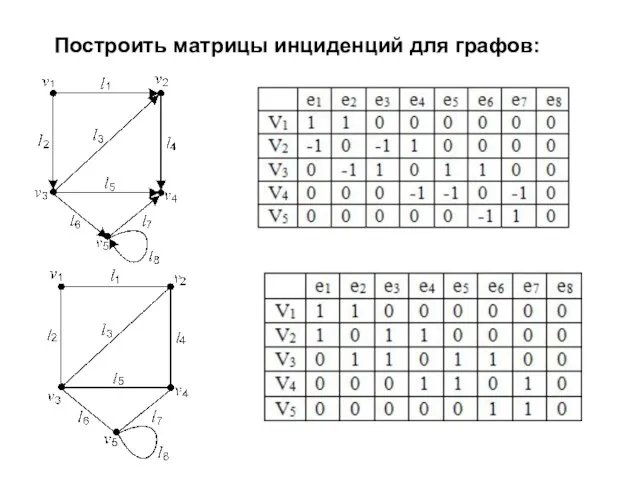
- 15. Построить матрицы инциденций для графов:
- 16. Свойства матриц инциденций для графов: Свойства матрицы инцидентности неориентированного графа. 1. Сумма элементов матрицы на i-й
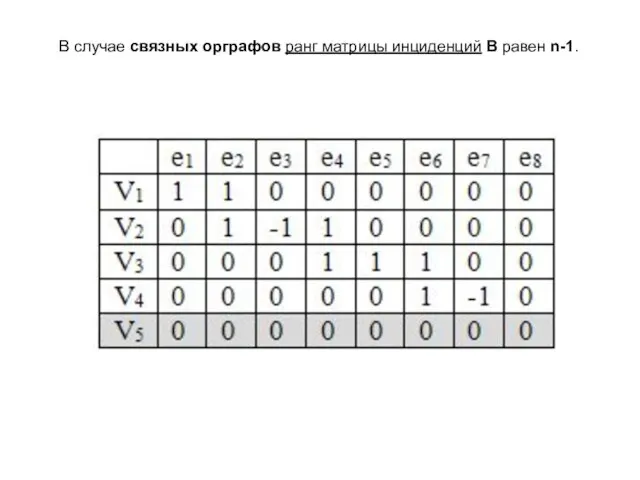
- 17. В случае связных орграфов ранг матрицы инциденций В равен n-1.
- 18. Построить матрицы инциденций для графов:
- 20. Скачать презентацию
![Матрица достижимостей R=[rij] Все диагональные элементы в матрице R равны](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/419834/slide-10.jpg)

![Матрица инциденций B=[bij] Если граф G ориентированный Если граф G](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/419834/slide-12.jpg)

 Программирование на языке Java. Методы класса
Программирование на языке Java. Методы класса Projektowanie aplikacji internetowych
Projektowanie aplikacji internetowych By Artem Morozov
By Artem Morozov Понятие дефекта.Виды дефектов.Bug Tracking Systems
Понятие дефекта.Виды дефектов.Bug Tracking Systems Python. Функции
Python. Функции Методы исследования динамических систем в среде matlab. (Лекция 1)
Методы исследования динамических систем в среде matlab. (Лекция 1) Растрлық және векторлық бағдарламалық құрылым. Компьютерлік графиканы қорытындылау
Растрлық және векторлық бағдарламалық құрылым. Компьютерлік графиканы қорытындылау Кодирование. Шифры. Защита информации
Кодирование. Шифры. Защита информации Электронные образовательные ресурсы нового поколения
Электронные образовательные ресурсы нового поколения Бирикс 24. Социальный интранет в облаке
Бирикс 24. Социальный интранет в облаке Файловые системы Windows
Файловые системы Windows Презентация к уроку Классификация компьютерных вирусов
Презентация к уроку Классификация компьютерных вирусов Создание комплексной автоматизированной системы управления. Ит в полиции
Создание комплексной автоматизированной системы управления. Ит в полиции Инструкция по работе с анкетой Naumen
Инструкция по работе с анкетой Naumen Оформление списка литературы. Библиографические БД
Оформление списка литературы. Библиографические БД Текстовый процесор Microsoft Word
Текстовый процесор Microsoft Word Косметология. Шаблон
Косметология. Шаблон Как создать компьютерный тест-пособие
Как создать компьютерный тест-пособие Создание приложений silverlight. (Лекция 4)
Создание приложений silverlight. (Лекция 4) Программирование циклических алгоритмов
Программирование циклических алгоритмов Структурный макет сайта
Структурный макет сайта Интервью
Интервью Структура веб-сайтів. Етапи створення веб-сайтів
Структура веб-сайтів. Етапи створення веб-сайтів Создание игры для изучение английского языка
Создание игры для изучение английского языка Каскадные таблицы стилей CSS
Каскадные таблицы стилей CSS Основные методологические аспекты проектирования информационной системы
Основные методологические аспекты проектирования информационной системы Середовища передавання даних
Середовища передавання даних -1763094957
-1763094957