Построение и анализ алгоритмов. Алгоритмы на графах. МОД в задаче коммивояжёра. (Лекция 6.2) презентация
Содержание
- 2. 01.03.2015 МОД в задаче коммивояжёра МОД как приближение в задаче коммивояжёра На лекции 2 рассматривались приближённые
- 3. 01.03.2015 МОД в задаче коммивояжёра Более точная терминология Лучше (более точно) называть это задачей коммивояжёра с
- 4. 01.03.2015 МОД в задаче коммивояжёра Оценка степени приближения алгоритмов АБС и АВБГ в евклидовом случае Nn
- 5. 01.03.2015 МОД в задаче коммивояжёра Новое: Приближённый алгоритм двойного обхода МОД при решении ЗК Для заданного
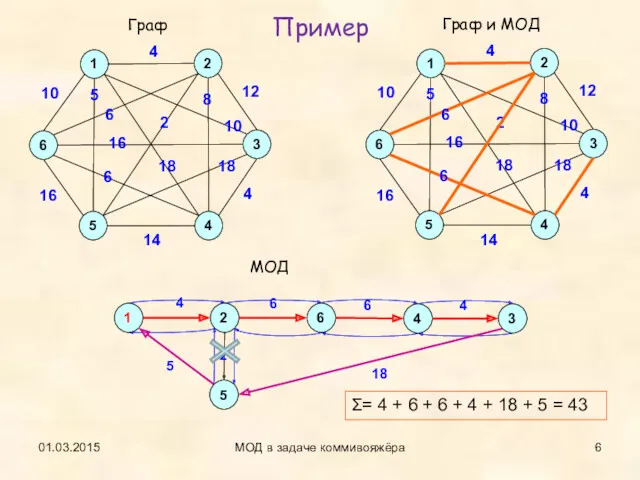
- 6. 01.03.2015 МОД в задаче коммивояжёра Пример Σ= 4 + 6 + 6 + 4 + 18
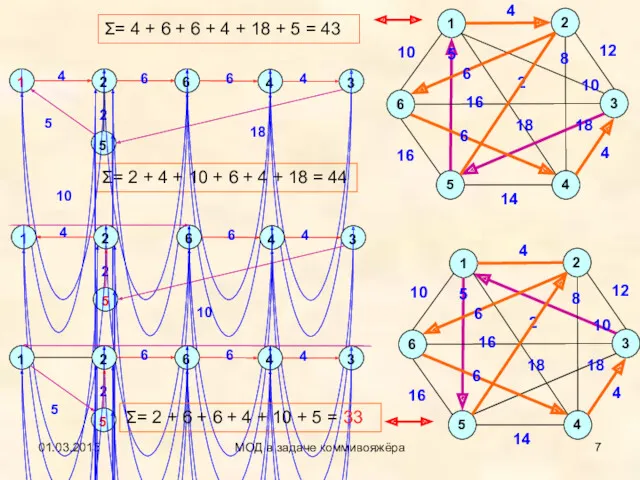
- 7. 01.03.2015 МОД в задаче коммивояжёра Σ= 2 + 4 + 10 + 6 + 4 +
- 8. 01.03.2015 МОД в задаче коммивояжёра Оценка приближения алгоритма двойного обхода МОД (АДО МОД) Пусть On –
- 9. 01.03.2015 МОД в задаче коммивояжёра Доказательство оценки Пусть есть оптимальный маршрут (цикл) On . Удалим одно
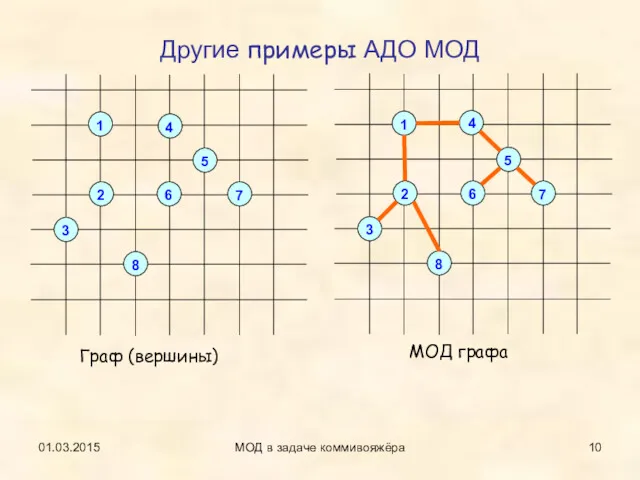
- 10. 01.03.2015 МОД в задаче коммивояжёра Другие примеры АДО МОД Граф (вершины) МОД графа
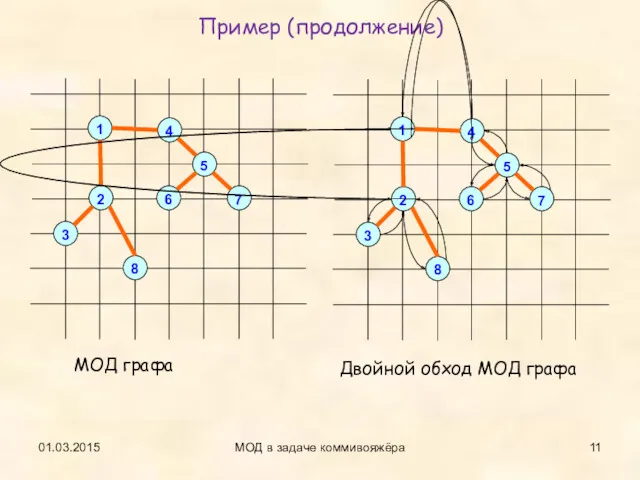
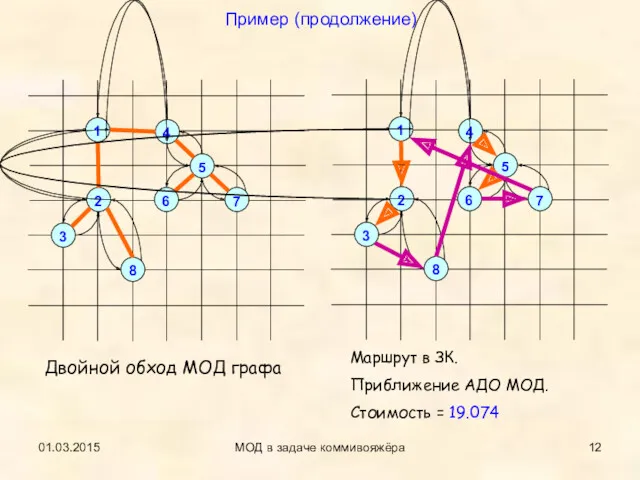
- 11. 01.03.2015 МОД в задаче коммивояжёра Пример (продолжение) МОД графа Двойной обход МОД графа
- 12. 01.03.2015 МОД в задаче коммивояжёра Маршрут в ЗК. Приближение АДО МОД. Стоимость = 19.074 Пример (продолжение)
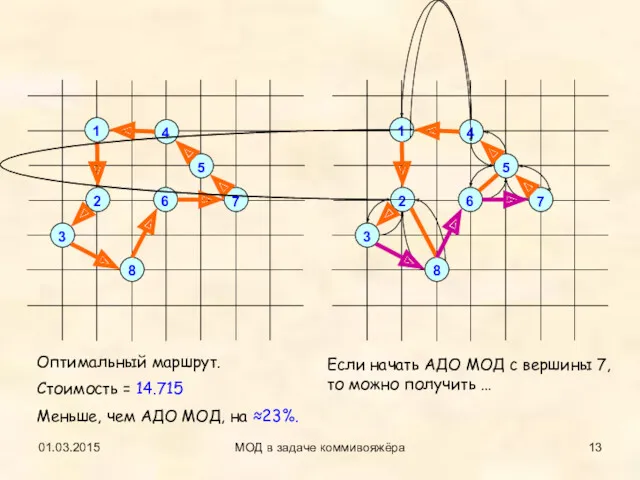
- 13. 01.03.2015 МОД в задаче коммивояжёра Оптимальный маршрут. Стоимость = 14.715 Меньше, чем АДО МОД, на ≈23%.
- 15. Скачать презентацию






 Государственная система научно-технической информации
Государственная система научно-технической информации Управление освещением витрины
Управление освещением витрины Контент. SEO текст
Контент. SEO текст Anatomy Lesson for Middle School Internal Organs of the Human Body
Anatomy Lesson for Middle School Internal Organs of the Human Body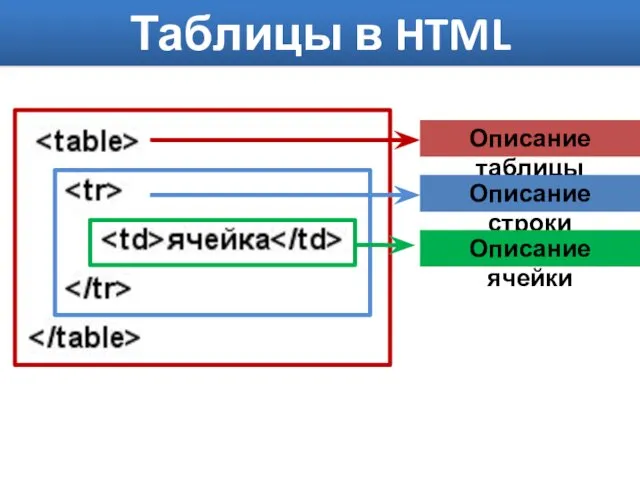 Таблицы в HTML
Таблицы в HTML Помехоустойчивое кодирование в системах телекоммуникаций (ПКСТ)
Помехоустойчивое кодирование в системах телекоммуникаций (ПКСТ) Решение задания ОГЭ по информатике
Решение задания ОГЭ по информатике Программирование (Python). Введение
Программирование (Python). Введение Кодирование, как изменение формы представления информации
Кодирование, как изменение формы представления информации Понятие информация. Виды информации. Основные информационные процессы
Понятие информация. Виды информации. Основные информационные процессы использование игр на уроке информатики в начальной школе
использование игр на уроке информатики в начальной школе Представление числовой информации в таблицах. Повторение
Представление числовой информации в таблицах. Повторение Каналы. Неименованные каналы
Каналы. Неименованные каналы Файловая система и ввод вывод информации
Файловая система и ввод вывод информации Overview software development methodology Аgile.Вusiness approach
Overview software development methodology Аgile.Вusiness approach Решение задач на компьютере. Алгоритмизация и программирование. 9 класс
Решение задач на компьютере. Алгоритмизация и программирование. 9 класс Интервью (событийное) как жанр журналистики (лекция № 6)
Интервью (событийное) как жанр журналистики (лекция № 6) Программирование. Оператор Mod в Visual Basic
Программирование. Оператор Mod в Visual Basic Перевод чисел из 10СС в 2СС
Перевод чисел из 10СС в 2СС Python NumPy. Установка. Массивы
Python NumPy. Установка. Массивы Декодирование. Построение префиксного кода по набору длин элементарных кодов
Декодирование. Построение префиксного кода по набору длин элементарных кодов Язык программирования C++
Язык программирования C++ Способы передачи данных. (Тема 4)
Способы передачи данных. (Тема 4) Графический дизайн для непрофессионалов
Графический дизайн для непрофессионалов Сущность и значение комплектования государственных архивов. Технотронные документы
Сущность и значение комплектования государственных архивов. Технотронные документы Автоматизированная информационная система Молодежь России. Регистрация в АИС
Автоматизированная информационная система Молодежь России. Регистрация в АИС Персональные данные (для детей 9-11 лет)
Персональные данные (для детей 9-11 лет) Создание комплексной системы непрерывного информационного обеспечения для повышение производительности качества сельхозпродукции
Создание комплексной системы непрерывного информационного обеспечения для повышение производительности качества сельхозпродукции