Содержание
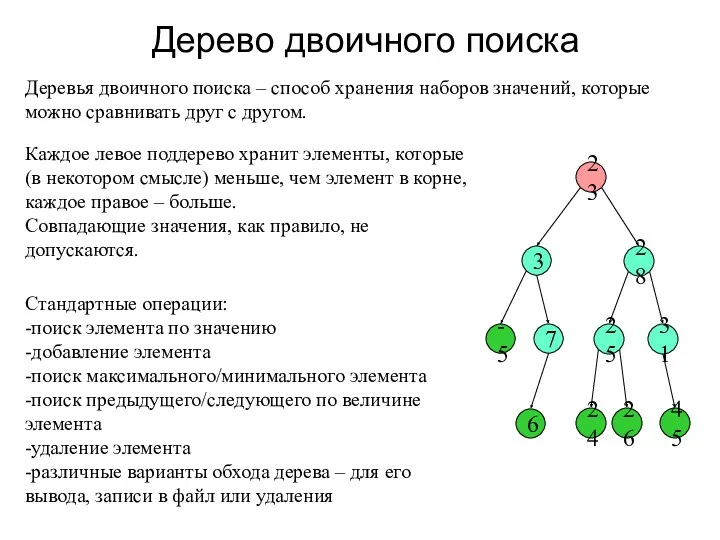
- 2. Дерево двоичного поиска Деревья двоичного поиска – способ хранения наборов значений, которые можно сравнивать друг с
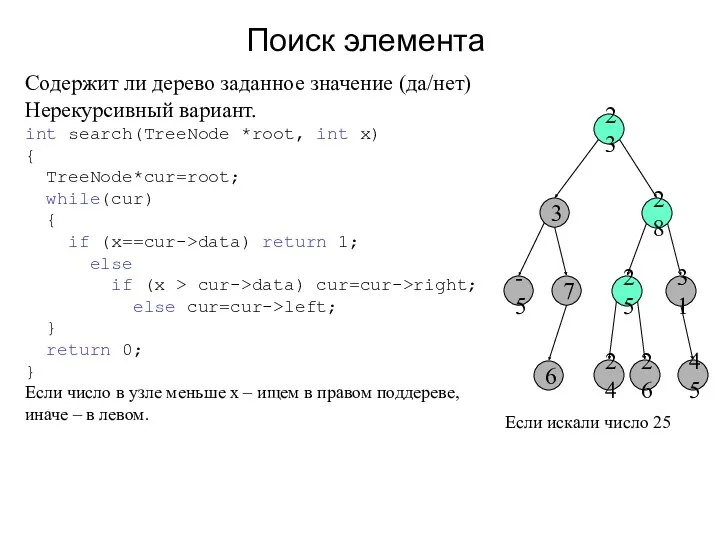
- 3. Поиск элемента -5 7 3 23 28 31 45 25 6 24 26 Содержит ли дерево
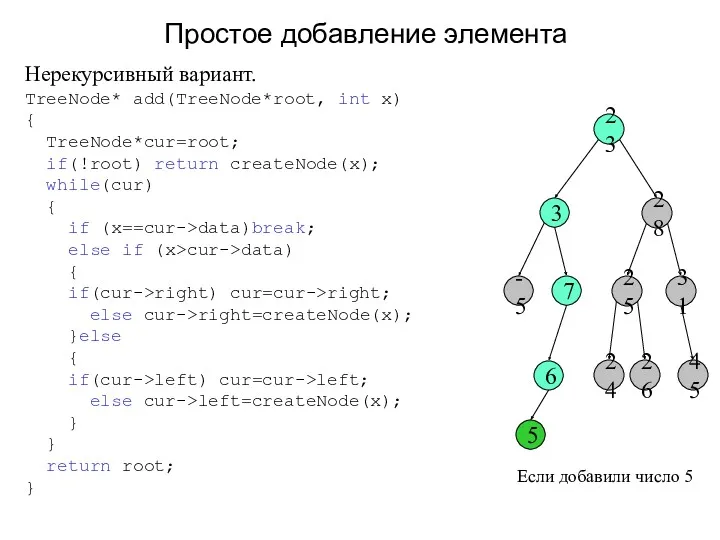
- 4. Простое добавление элемента -5 7 3 23 28 31 45 25 6 24 26 Нерекурсивный вариант.
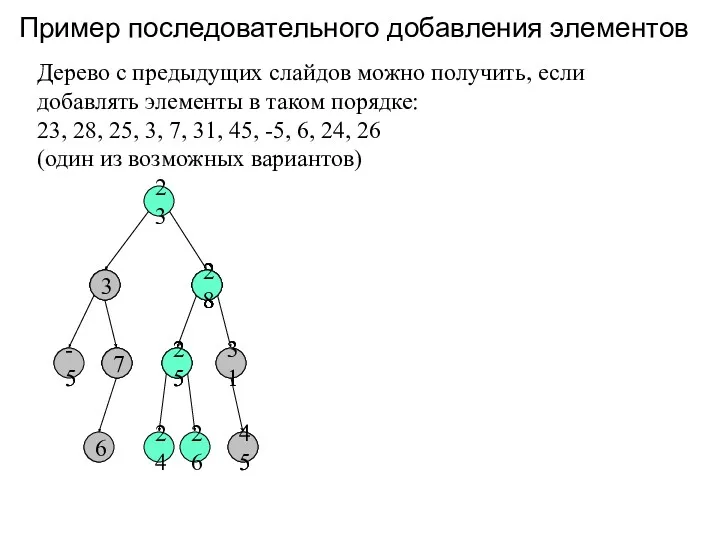
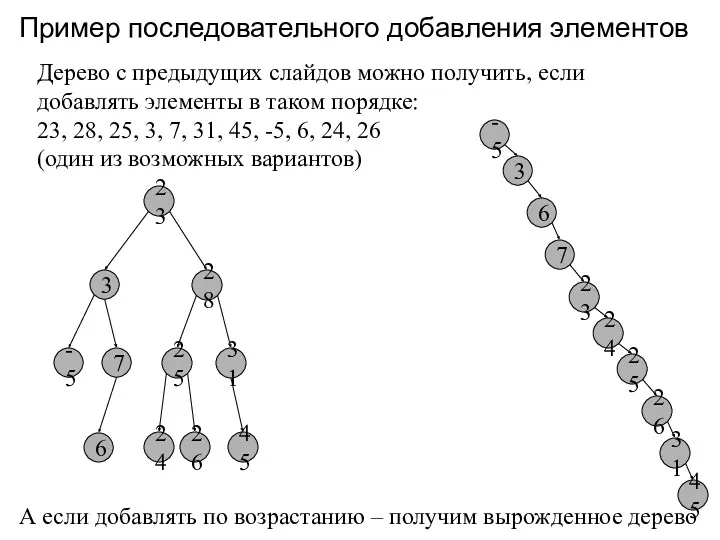
- 5. Пример последовательного добавления элементов 23 Дерево с предыдущих слайдов можно получить, если добавлять элементы в таком
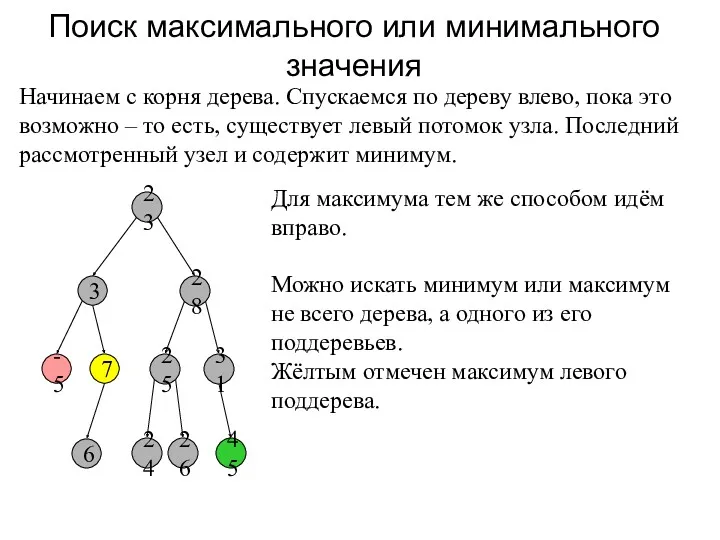
- 6. Поиск максимального или минимального значения 23 3 28 -5 7 25 31 45 6 24 26
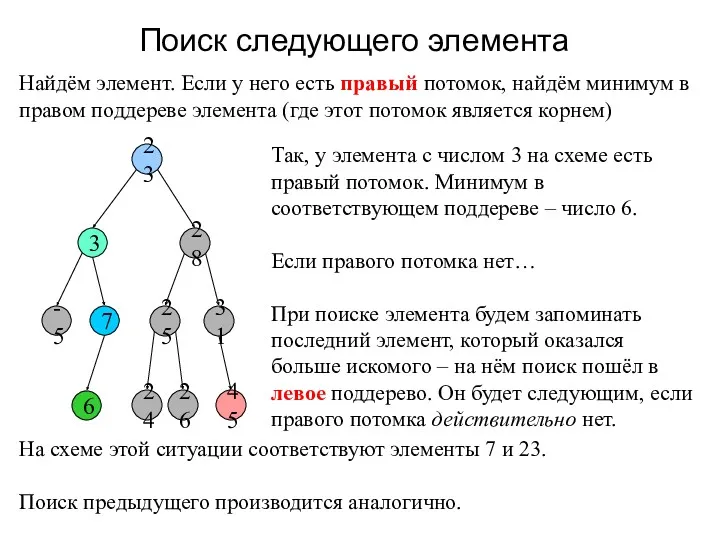
- 7. Поиск следующего элемента 23 3 28 -5 7 25 31 45 6 24 26 Найдём элемент.
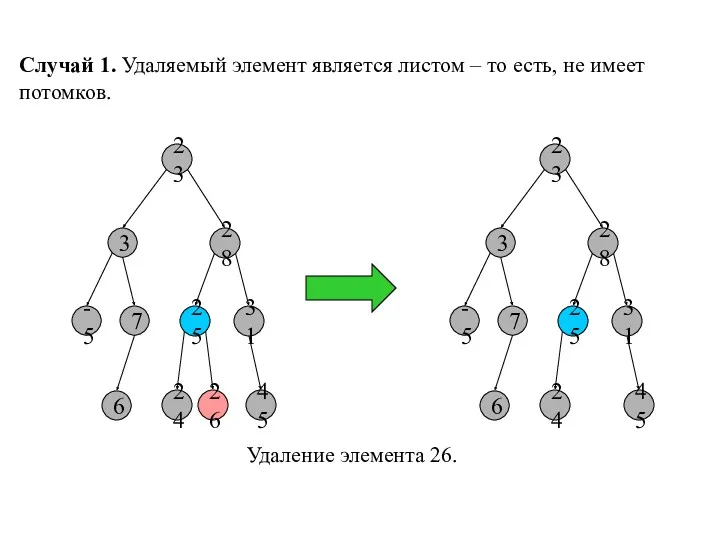
- 8. Варианты простого удаления элемента Случай 1. Удаляемый элемент является листом – то есть, не имеет потомков.
- 9. Случай 1. Удаляемый элемент является листом – то есть, не имеет потомков. 23 3 28 -5
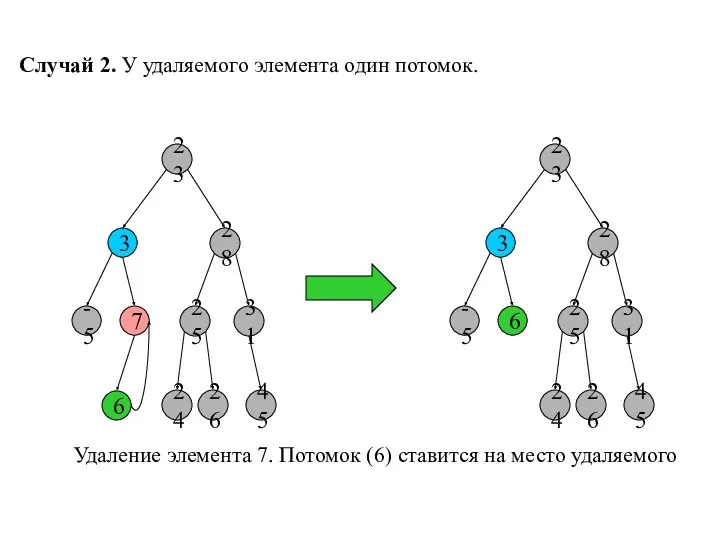
- 10. Случай 2. У удаляемого элемента один потомок. 23 3 28 -5 7 25 31 45 6
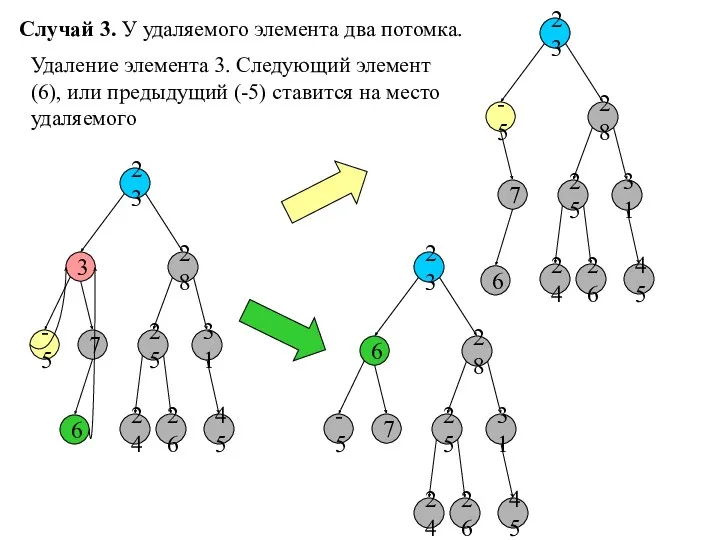
- 11. Случай 3. У удаляемого элемента два потомка. 23 3 28 -5 7 25 31 45 6
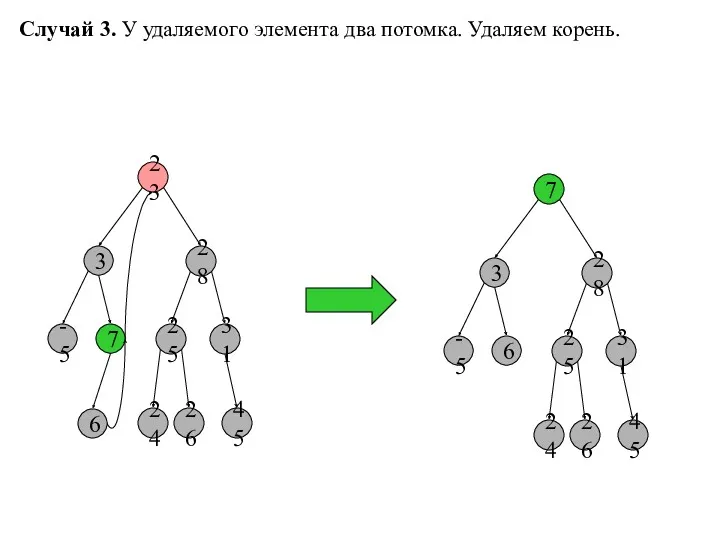
- 12. Случай 3. У удаляемого элемента два потомка. Удаляем корень. 23 3 28 -5 7 25 31
- 13. Пример последовательного добавления элементов 23 3 28 -5 7 25 31 45 6 24 26 Дерево
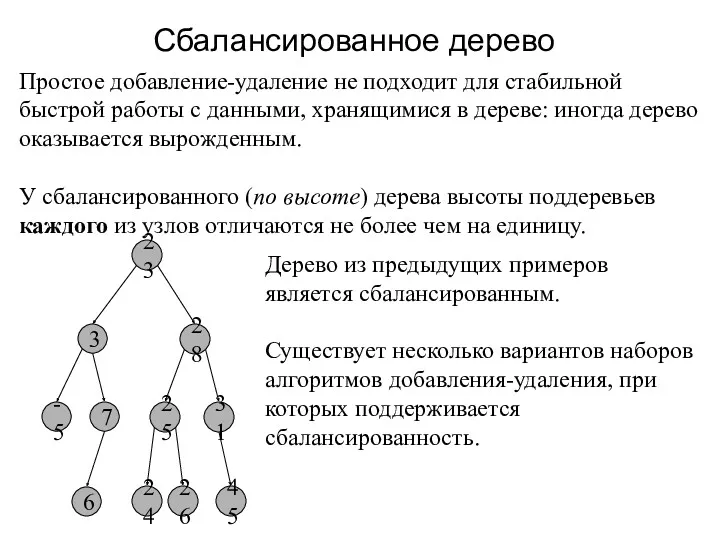
- 14. Сбалансированное дерево Простое добавление-удаление не подходит для стабильной быстрой работы с данными, хранящимися в дереве: иногда
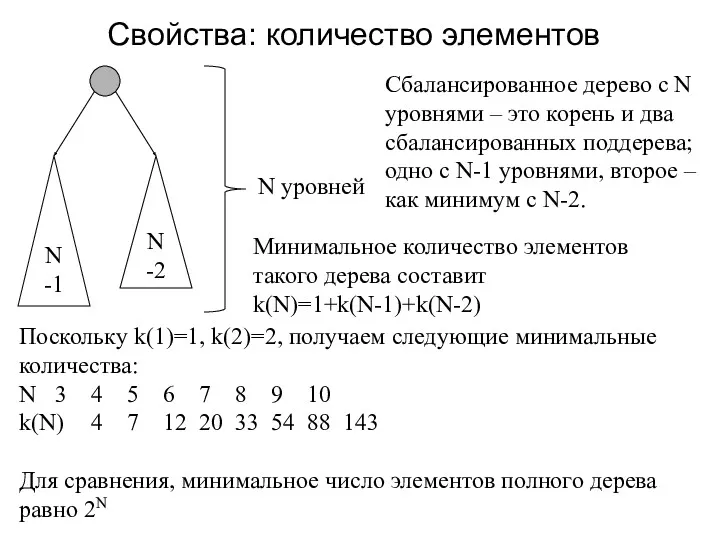
- 15. Свойства: количество элементов N-1 N-2 N уровней Сбалансированное дерево с N уровнями – это корень и
- 16. АВЛ-дерево Один из вариантов сбалансированного (по высоте) дерева, назван по фамилиям авторов 1962, «Один алгоритм организации
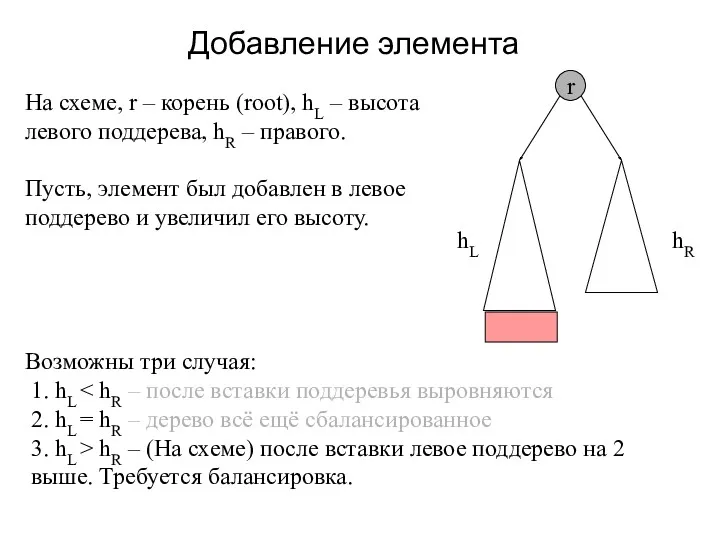
- 17. Добавление элемента r hL hR На схеме, r – корень (root), hL – высота левого поддерева,
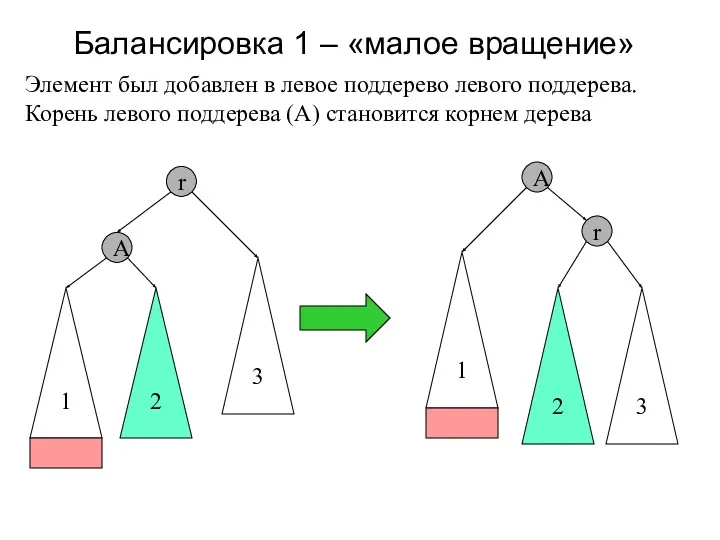
- 18. Балансировка 1 – «малое вращение» r 2 3 A 1 Элемент был добавлен в левое поддерево
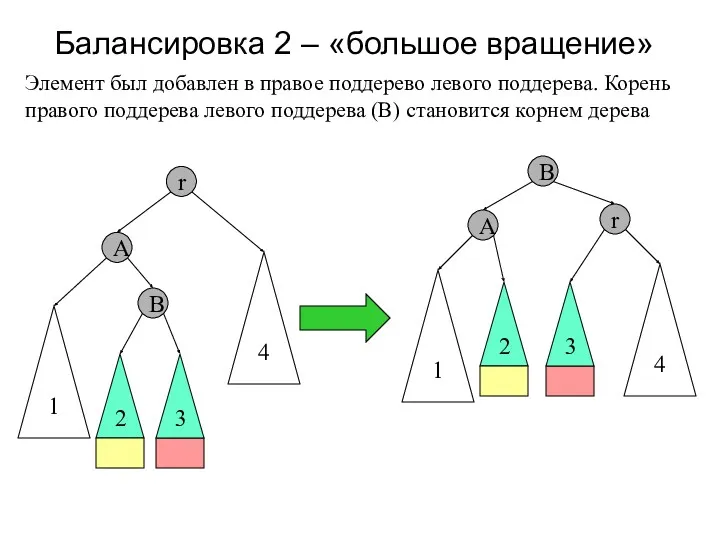
- 19. Балансировка 2 – «большое вращение» r 2 4 A 1 Элемент был добавлен в правое поддерево
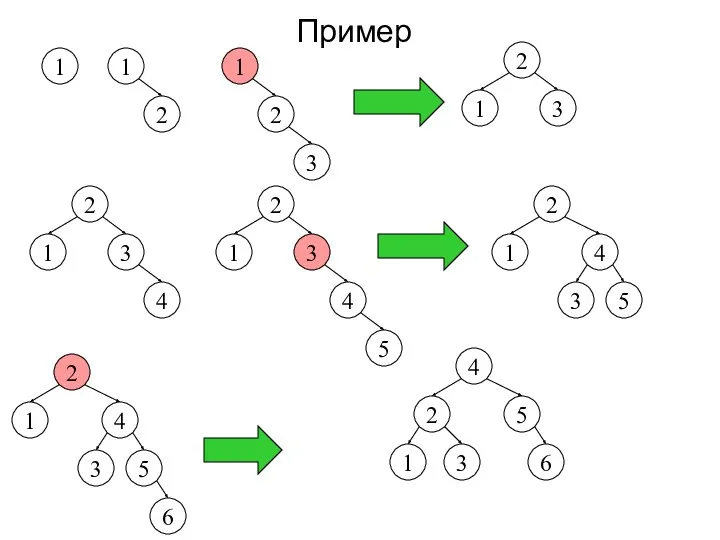
- 20. Пример 1 1 2 1 2 3 2 3 1 2 3 1 4 2 3
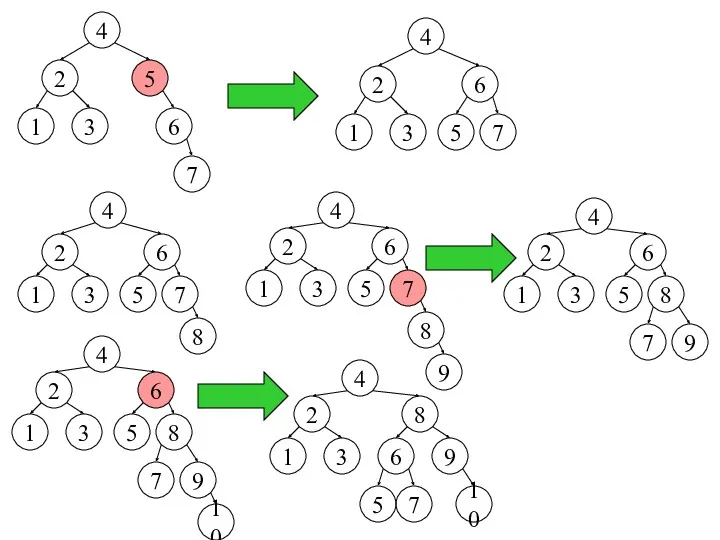
- 21. 4 2 3 5 6 1 7 4 2 3 5 6 1 7 4 2
- 22. АВЛ – дерево, комментарии Балансировка при добавлении в правое поддерево делается симметрично. Если расход памяти важен,
- 23. Красно-чёрное дерево Rudolf Bayer 1972, «Symmetric Binary B-Trees. Data Structure and Maintenance Algorithms» Красно-чёрными деревьями эти
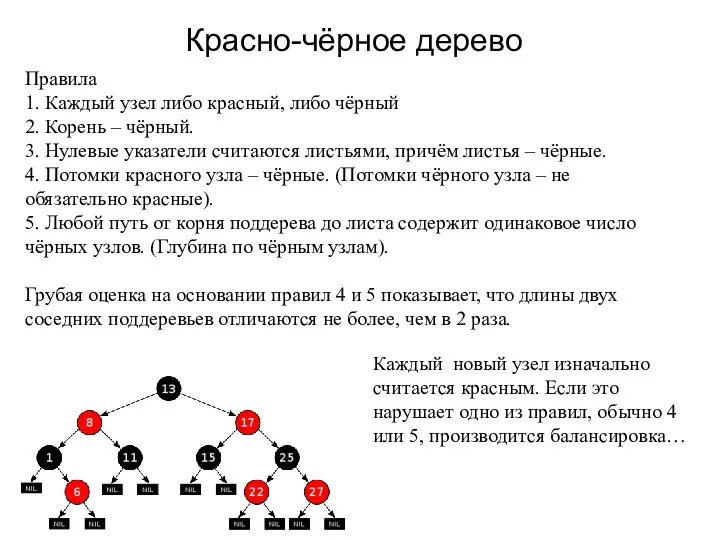
- 24. Красно-чёрное дерево Правила 1. Каждый узел либо красный, либо чёрный 2. Корень – чёрный. 3. Нулевые
- 26. Скачать презентацию



 Частная усадьба
Частная усадьба Ионное легирование полупроводников
Ионное легирование полупроводников Алгоритмы компьютерной графики. (Тема 3)
Алгоритмы компьютерной графики. (Тема 3) Visio бағдарламалық Aray Deluxe мейрамхана сайтының жобасын басқару
Visio бағдарламалық Aray Deluxe мейрамхана сайтының жобасын басқару Основные понятия теории баз данных
Основные понятия теории баз данных Цифровизация производства
Цифровизация производства Безопасный Интернет
Безопасный Интернет Antivirus dasturiy vositalar: kompyuter viruslarining xarakteristikalari, viruslarni aniqlash va ulardan himoya qilish
Antivirus dasturiy vositalar: kompyuter viruslarining xarakteristikalari, viruslarni aniqlash va ulardan himoya qilish Сравнение современных СУБД
Сравнение современных СУБД LINQ - технология
LINQ - технология Одномерные массивы. Сортировка массива
Одномерные массивы. Сортировка массива Phraseology as a branch of linguistics
Phraseology as a branch of linguistics Алгоритм ветвление
Алгоритм ветвление Intencje i przechowywanie danych
Intencje i przechowywanie danych Использование Интернет-ресурсов при подготовке исследовательской работы
Использование Интернет-ресурсов при подготовке исследовательской работы Программные средства машинной графики. Введение в интерактивную машинную графику (Тема №2)
Программные средства машинной графики. Введение в интерактивную машинную графику (Тема №2) Путешествие по карте. Множества или - или. 3 класс
Путешествие по карте. Множества или - или. 3 класс IPC. Product Lines. Roadmap
IPC. Product Lines. Roadmap Керування оперативною пам’яттю
Керування оперативною пам’яттю Текстовый процессор Microsoft Word 2003. Технология обработки текстовой информации
Текстовый процессор Microsoft Word 2003. Технология обработки текстовой информации Визуализация информации в текстовых документах
Визуализация информации в текстовых документах Анимация средствами CSS. (Часть 5)
Анимация средствами CSS. (Часть 5) Внеклассное мероприятие для недели информатики: Игра Крестики-нолики.
Внеклассное мероприятие для недели информатики: Игра Крестики-нолики.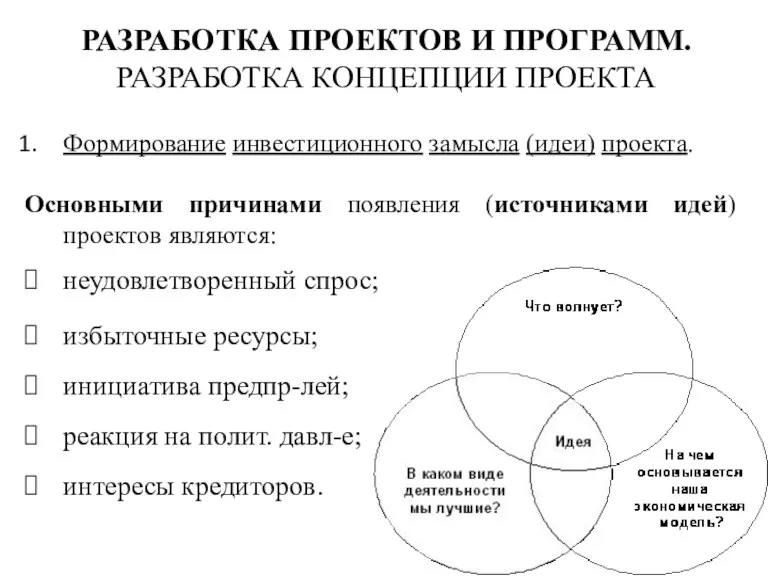 Разработка концепции проекта. (Лекция 4)
Разработка концепции проекта. (Лекция 4) Урок-игра по информатике
Урок-игра по информатике Содержание и объем ГОТ, 7 класс
Содержание и объем ГОТ, 7 класс Программное обеспечение
Программное обеспечение Урок информатики в 1 классе. Виды информации.
Урок информатики в 1 классе. Виды информации.