Содержание
- 2. DES
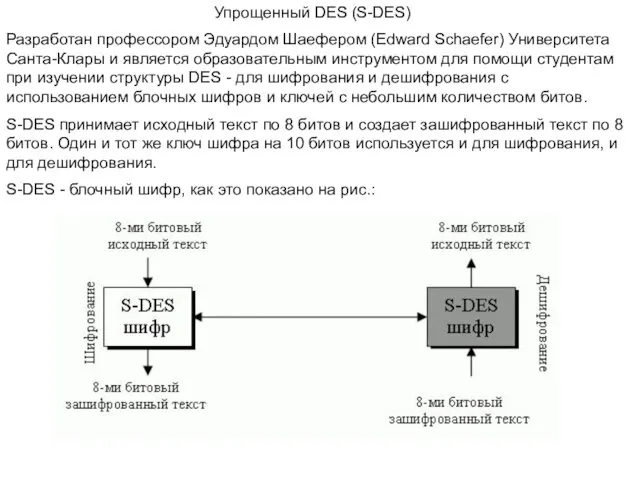
- 3. Упрощенный DES (S-DES) Разработан профессором Эдуардом Шаефером (Edward Schaefer) Университета Санта-Клары и является образовательным инструментом для
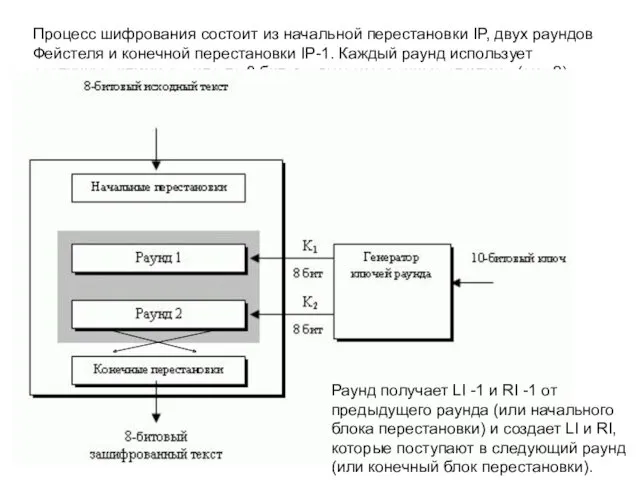
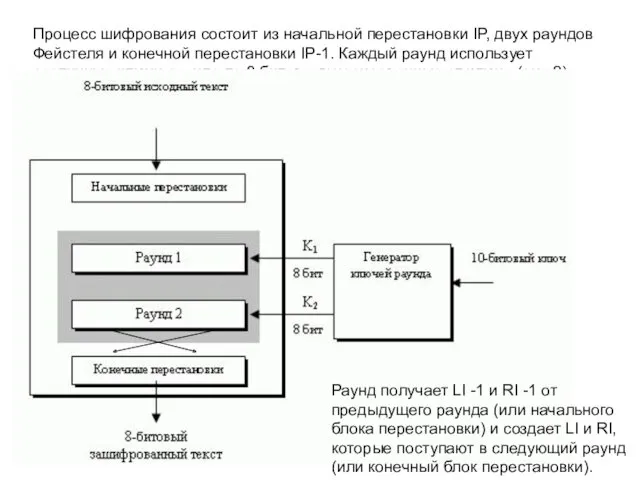
- 4. Процесс шифрования состоит из начальной перестановки IP, двух раундов Фейстеля и конечной перестановки IP-1. Каждый раунд
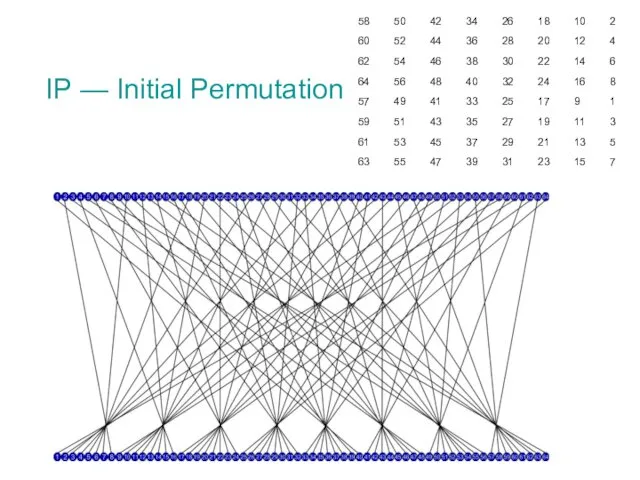
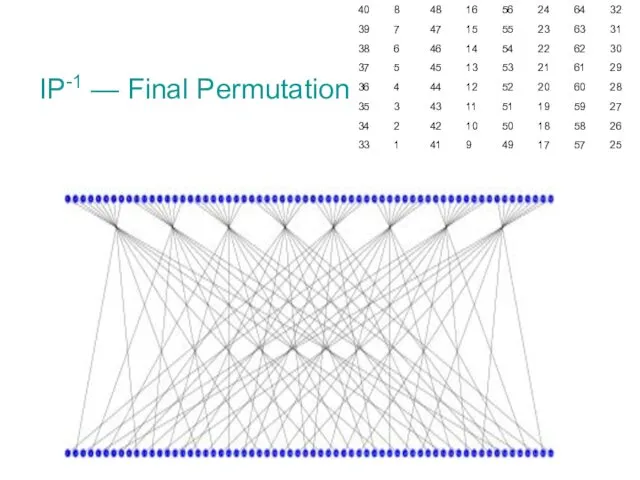
- 5. IP: [12345678]->[26314857]. IP-1:[12345678]->[41357286]. Начальная и конечная перестановка Пример: Шифротекст:
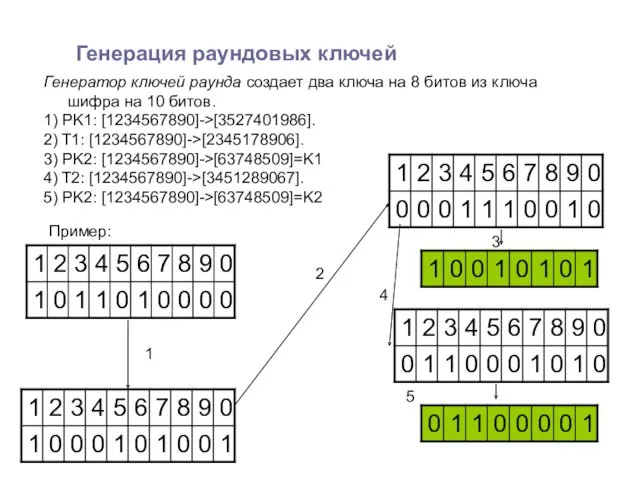
- 6. Генерация раундовых ключей Генератор ключей раунда создает два ключа на 8 битов из ключа шифра на
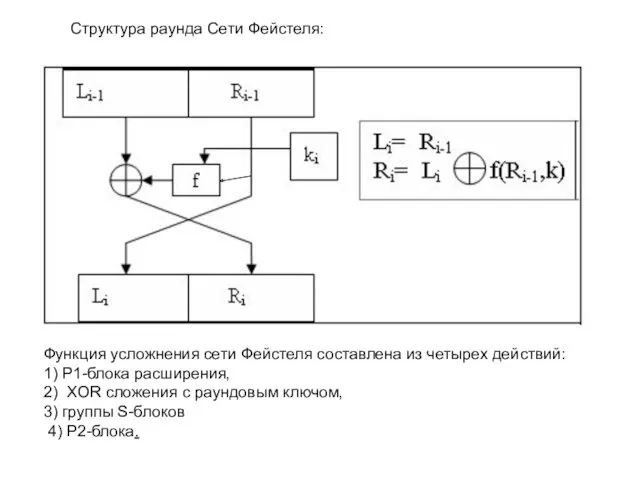
- 7. Функция усложнения сети Фейстеля составлена из четырех действий: 1) P1-блока расширения, 2) XOR сложения с раундовым
- 8. P1 :[1234]->[41232341]. P1-блок расширения: Пример.
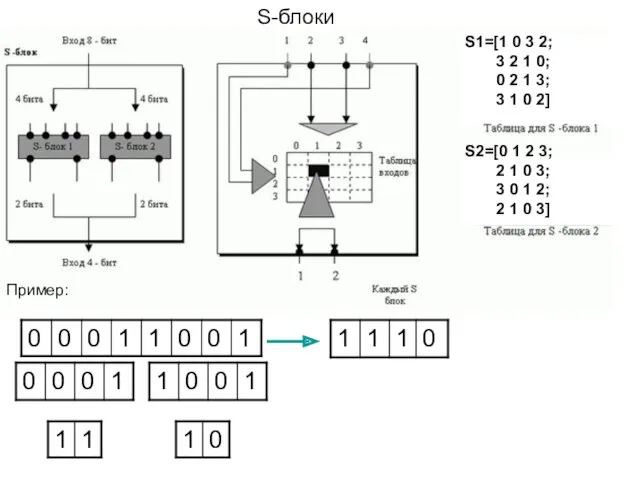
- 9. S-блоки Пример: S1=[1 0 3 2; 3 2 1 0; 0 2 1 3; 3 1
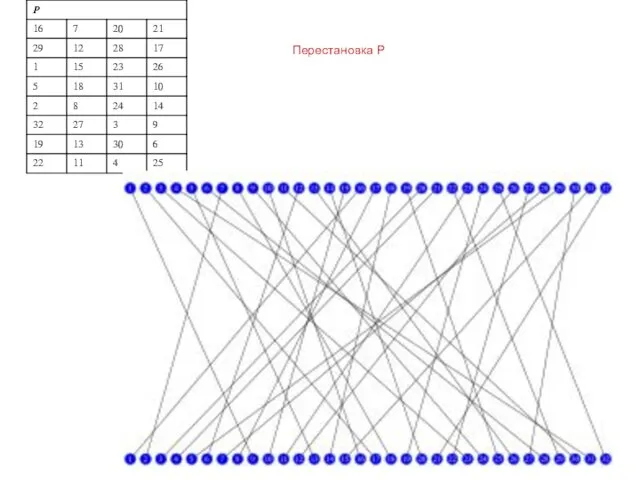
- 10. P2: [1234]->[2431]. Перестановка P2
- 11. Процесс шифрования состоит из начальной перестановки IP, двух раундов Фейстеля и конечной перестановки IP-1. Каждый раунд
- 12. История В 1972 году было проведено исследование потребности правительства США в компьютерной безопасности. Американское «национальное бюро
- 13. Алгоритм DES – шифр Фейстеля со следующими параметрами 1) 64 – битные блоки; 2) 56 битный
- 15. IP — Initial Permutation
- 16. IP-1 — Final Permutation
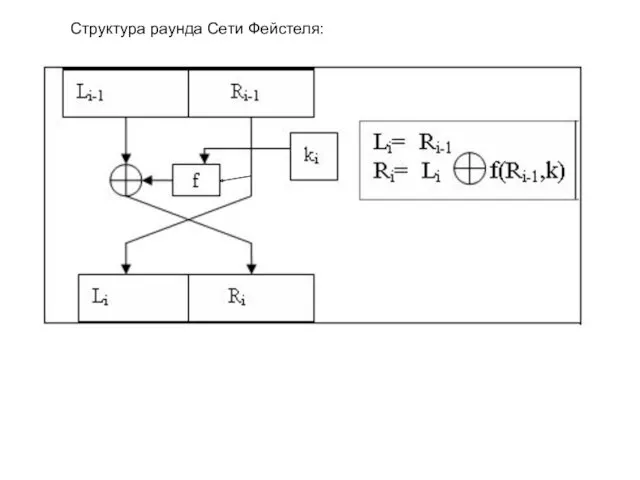
- 17. Структура раунда Сети Фейстеля:
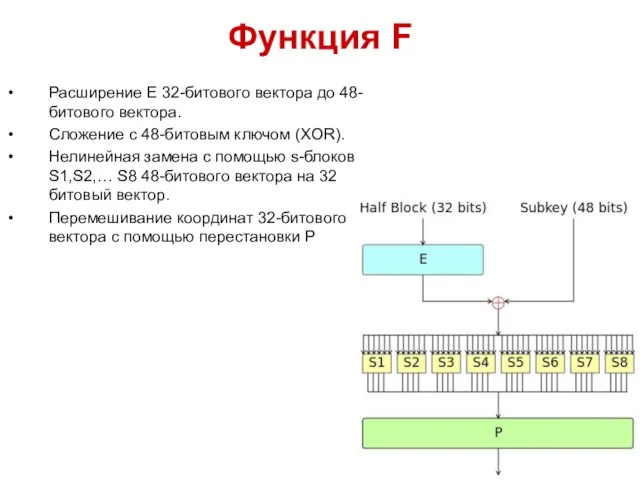
- 18. Функция F Расширение E 32-битового вектора до 48-битового вектора. Сложение с 48-битовым ключом (XOR). Нелинейная замена
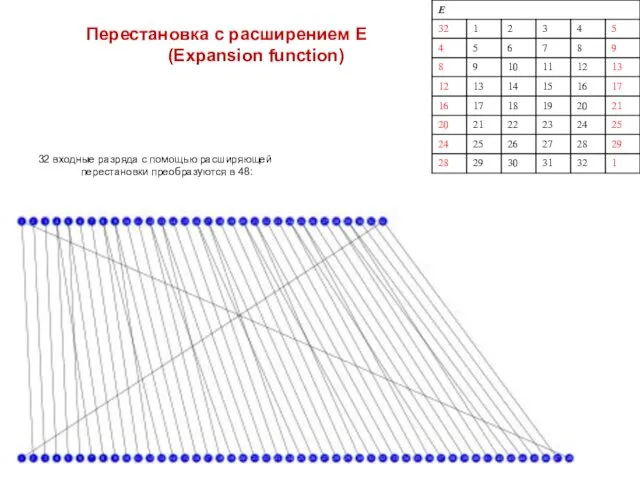
- 19. Перестановка с расширением E (Expansion function) 32 входные разряда с помощью расширяющей перестановки преобразуются в 48:
- 20. 2. «Подмешивание» циклового ключа Значение на выходе ключевого сумматора получается в результате побитового сложения сформированного 48-разрядного
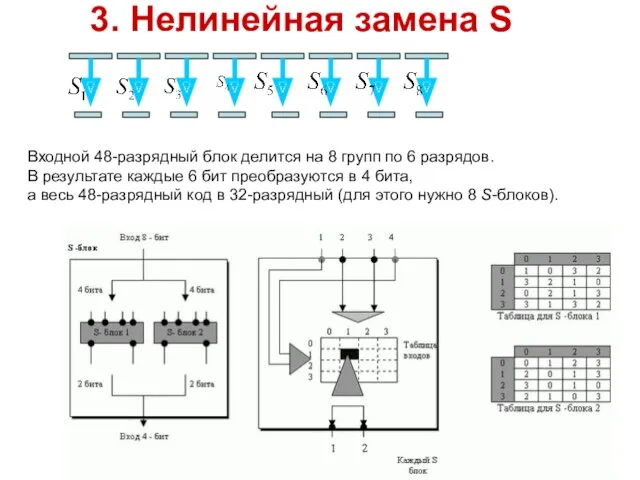
- 21. 3. Нелинейная замена S Входной 48-разрядный блок делится на 8 групп по 6 разрядов. В результате
- 22. Конструкция S-блока S-блоки представляют собой таблицы, содержащие 4 строки и 16 столбцов. Первый и последний разряд
- 23. Перестановка P
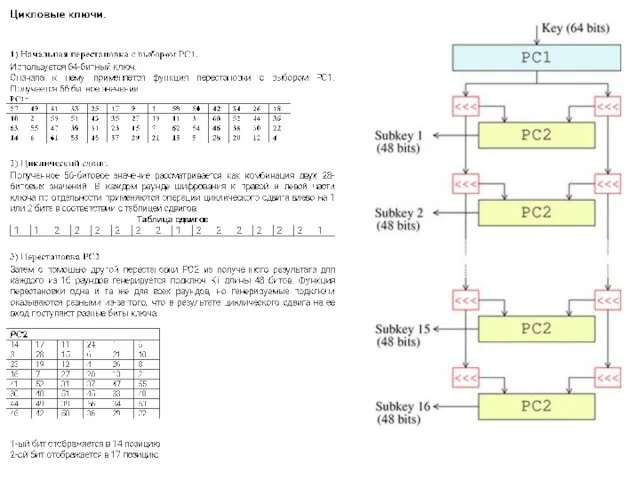
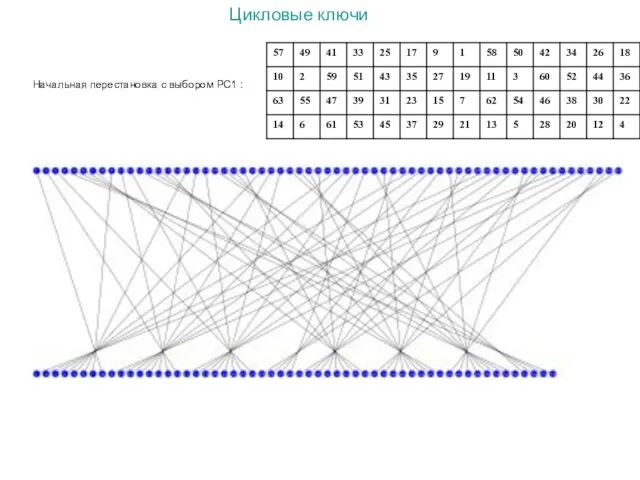
- 25. Цикловые ключи Начальная перестановка с выбором PC1 :
- 27. 2. Циклический сдвиг. Полученное 56-битовое значение рассматривается как комбинация двух 28-битовых значений. В каждом раунде шифрования
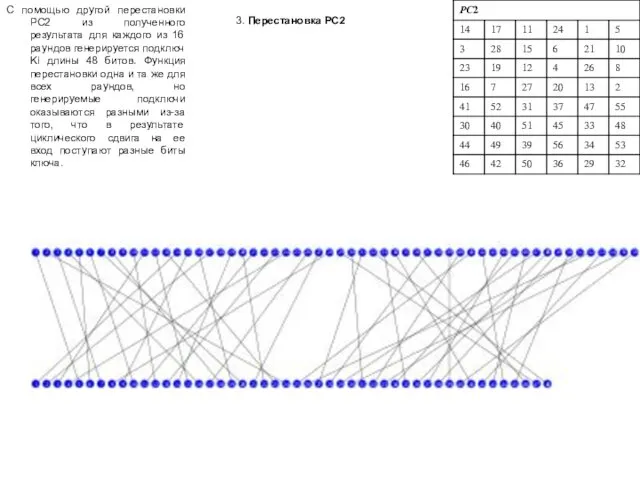
- 28. 3. Перестановка PC2 С помощью другой перестановки PC2 из полученного результата для каждого из 16 раундов
- 29. Прямое и обратное преобразование сети Фейстеля Minor cryptanalytic properties DES exhibits the complementation property, namely that
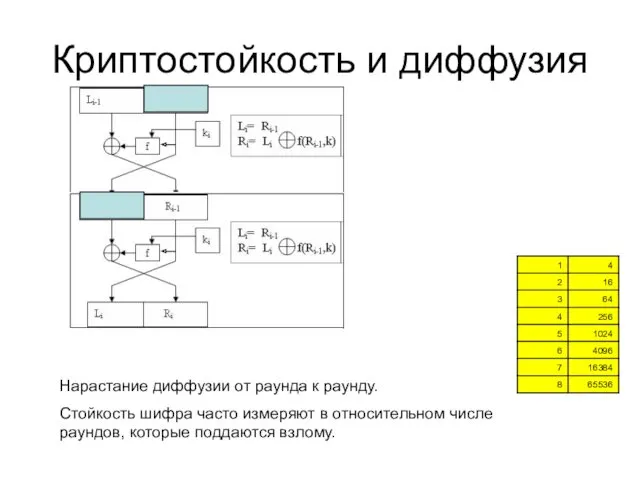
- 30. Криптостойкость и диффузия Нарастание диффузии от раунда к раунду. Стойкость шифра часто измеряют в относительном числе
- 31. Brute force attack For DES, questions were raised about the adequacy of its key size early
- 32. 1. Японский специалист Мицуру Мацуи (Mitsuru Matsui), изобретатель линейного криптоанализа, в 1993 году доказал возможность вычисления
- 33. Кроме того, практически сразу после появления DES были обнаружены следующие проблемы с ключами шифрования DES [4]:
- 34. DESX Метод DESX создан Рональдом Ривестом и формально продемонстрирована Killian и Rogaway. Этод метод — усиленный
- 35. Отечественный стандарт шифрования ГОСТ 28147-89 ГОСТ 28147-89 - это стандарт, принятый в 1989 году в Советском
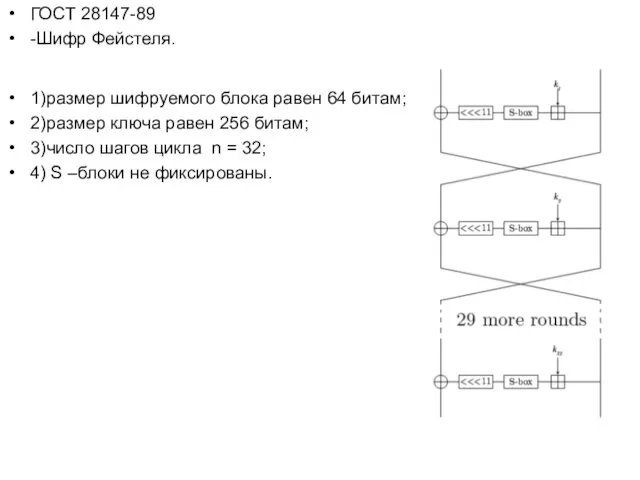
- 36. ГОСТ 28147-89 -Шифр Фейстеля. 1)размер шифруемого блока равен 64 битам; 2)размер ключа равен 256 битам; 3)число
- 37. 4)получение цикловых ключей Ключ К длины 256 битов разбивается на блоки длиной 32 бит: К =
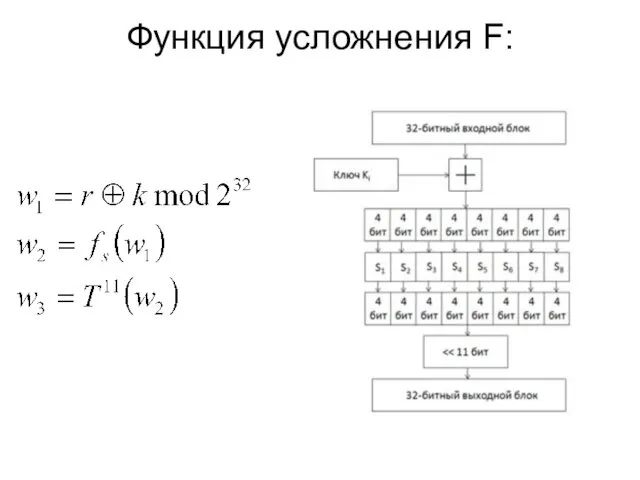
- 38. Функция усложнения F:
- 39. Таблица замен в ГОСТе - аналог S-блоков DES'а - представляет собой таблицу (матрицу) размером 8x16, содержащую
- 40. В настоящее время известны S-boxes, которые используются в приложениях Центрального Банка РФ и считаются достаточно сильными.
- 41. Криптоанализ В мае 2011 года известный криптоаналитик Николя Куртуа заявил об обнаружении серьезных уязвимостей в данном
- 42. Сравнение ГОСТ и DES
- 43. в DES сложная генерация подключей из ключей, а в ГОСТ простая. в DES 56-битный ключ, а
- 44. DES использует гораздо более сложную процедуру создания подключей, чем ГОСТ 28147. В ГОСТ эта процедура очень
- 45. ГОСТ не запантентован, поэтому его может свободно использовать любое юридическое и физическое лицо, если, конечно, это
- 46. Слабые ключи DES и ГОСТ Слабыми ключами называется ключи k такие, что Ek Ek(x)=x , где
- 47. Алгоритм IDEA International Data Encryption Algorithm IDEA является одним из нескольких симметричных криптографических алгоритмов, которыми первоначально
- 48. Алгоритм IDEA International Data Encryption Algorithm IDEA является одним из нескольких симметричных криптографических алгоритмов, которыми первоначально
- 49. Частично основан на структуре FEAL 1)размер блока 64 бита; 2) размер ключа 128 битов; 3) число
- 50. Безопасность IDEA основывается на использовании трех не совместимх типов арифметических операций над 16-битными словами. В ходе
- 51. Ключевое расписание Ключ K 128 бит. Получаем 52 раундовых ключа – 6 на каждый их 8
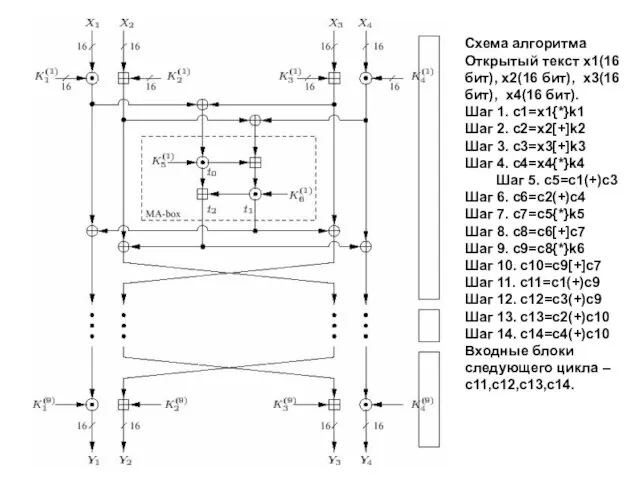
- 52. Схема алгоритма Открытый текст x1(16 бит), x2(16 бит), x3(16 бит), x4(16 бит). Шаг 1. c1=x1{*}k1 Шаг
- 53. Выходное отображение После 8 цикла реализуется выходное отображение Шаг 1. y1=x1(9){*}k1(9) Шаг 2. y2=x2(9)[+]k2(9) Шаг 3.
- 54. Расшифровка Метод вычисления, использующийся для расшифровки текста по существу такой же, как и при его шифровании.
- 55. Аппаратная реализация Аппаратная реализация имеет перед программной следующие преимущества: существенное повышение скорости шифрования за счёт использования
- 56. Развитие аппаратных реализаций IDEA 1998программная 23,53Мб/сек Limpaa 2000программная 44Мб/сек Limpaa 1992ASIC1992ASIC 1,5 мкм КМОП44Мб/сек Bonnenberg и
- 57. Брюс Шнайер отозвался об IDEA так: «Мне кажется, это самый лучший и надежный блочный алгоритм, опубликованный
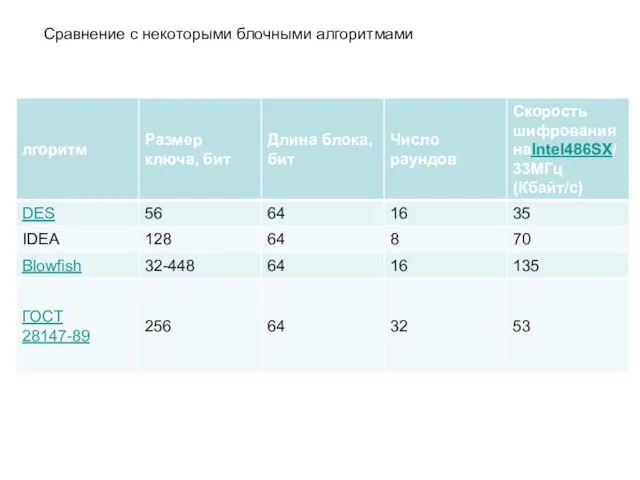
- 58. Сравнение с некоторыми блочными алгоритмами
- 59. Преимущества и недостатки IDEA Преимущества В программной реализации на Intel486SX по сравнению с DES IDEA в
- 60. Применение IDEA Алгоритм IDEA является торговой маркой и запатентован в Австрии, Франции, Германии, Италии, Нидерландах, Испании,
- 61. Недостатки DES
- 62. Double DES Наиболее логичным способом противодействия полному перебору ключа DES выглядит многократное зашифрование данных алгоритмом DES
- 63. Атака «встреча посередине» предложена Ральфом Мерклем (Ralph Merkle) и Мартином Хеллманом . С помощью этой атаки
- 64. Тройной DES Достаточно медленно работает, так что некоторые приложения не могут работать по этим алгоритмом. Так
- 65. AES
- 66. В 80-х годах в США был принят стандарт симметричного криптоалгоритма для внутреннего применения DES (Data Encryption
- 67. алгоритм должен быть симметричным, алгоритм должен быть блочным шифром, алгоритм должен иметь длину блока 128 бит,
- 68. использовать операции, легко реализуемые как аппаратно, так и программно, ориентироваться на 32-разрядные процессоры, не усложнять без
- 69. На первом этапе в оргкомитет соревнования поступило 15 заявок из совершенно разных уголков мира. В течение
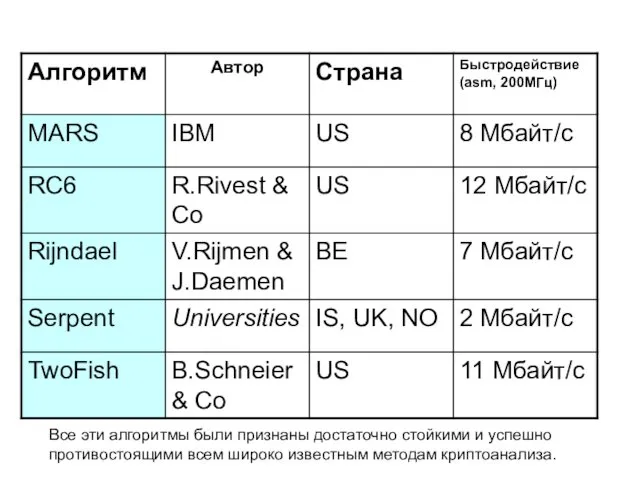
- 70. 5 финалистов AES Все эти алгоритмы были признаны достаточно стойкими и успешно противостоящими всем широко известным
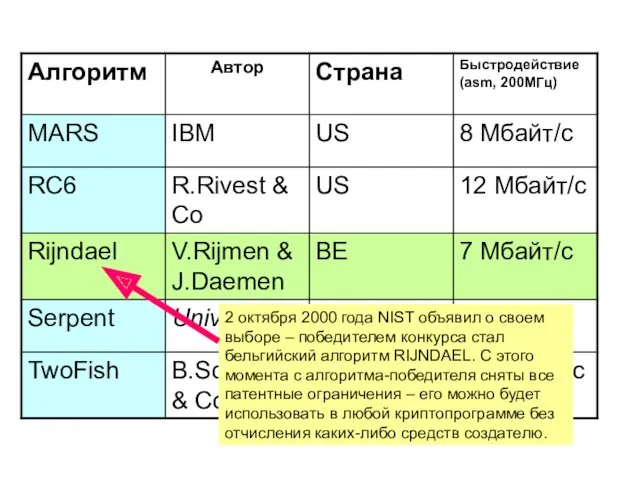
- 71. 5 финалистов AES 2 октября 2000 года NIST объявил о своем выборе – победителем конкурса стал
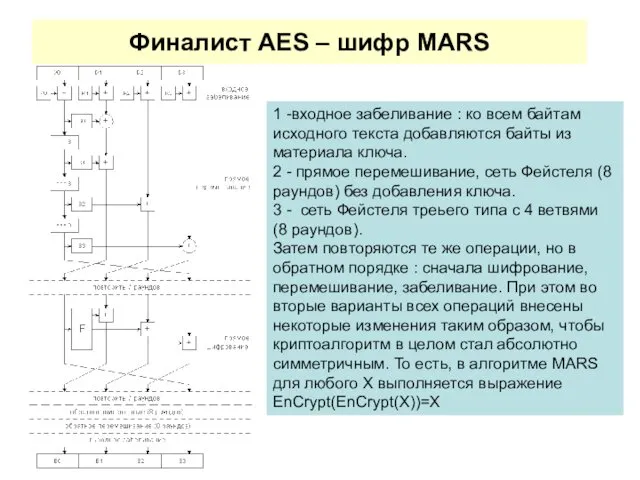
- 72. Финалист AES – шифр MARS 1 -входное забеливание : ко всем байтам исходного текста добавляются байты
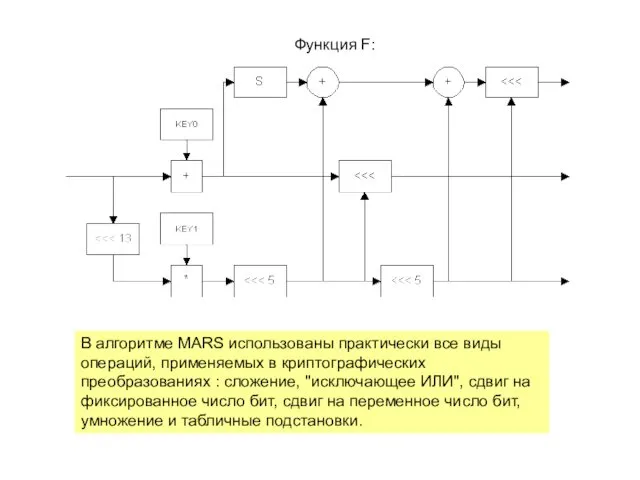
- 73. Функция F: В алгоритме MARS использованы практически все виды операций, применяемых в криптографических преобразованиях : сложение,
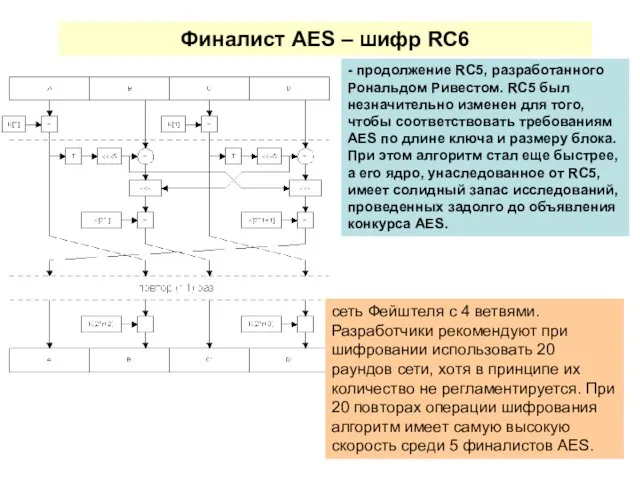
- 74. Финалист AES – шифр RC6 - продолжение RC5, разработанного Рональдом Ривестом. RC5 был незначительно изменен для
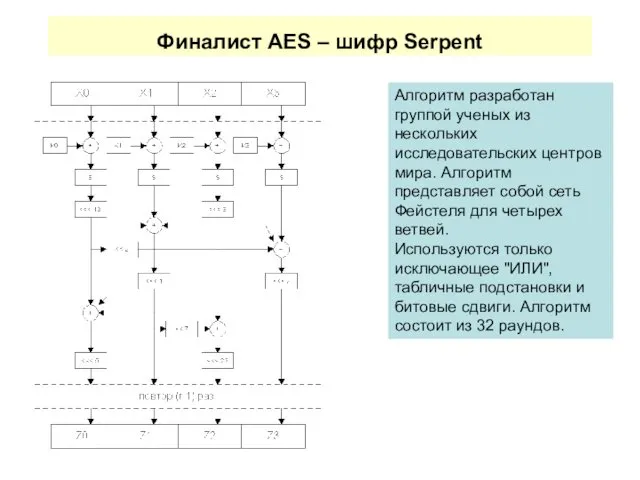
- 75. Финалист AES – шифр Serpent Алгоритм разработан группой ученых из нескольких исследовательских центров мира. Алгоритм представляет
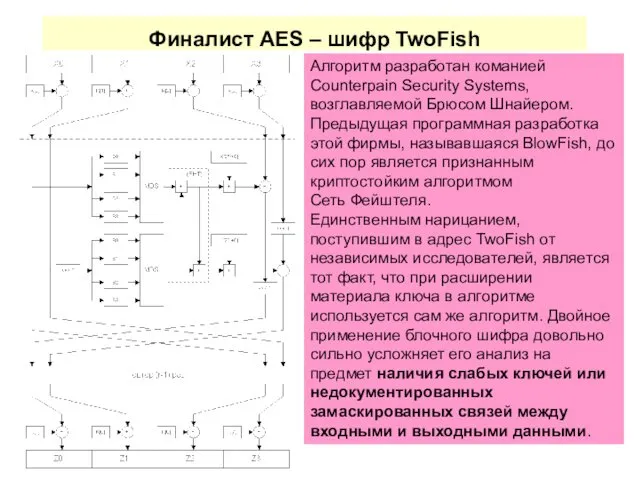
- 76. Финалист AES – шифр TwoFish Алгоритм разработан команией Counterpain Security Systems, возглавляемой Брюсом Шнайером. Предыдущая программная
- 77. Победитель AES – шифр Rijndael Не использует сеть Фейстеля для криптопреобразований. Алгоритм представляет каждый блок кодируемых
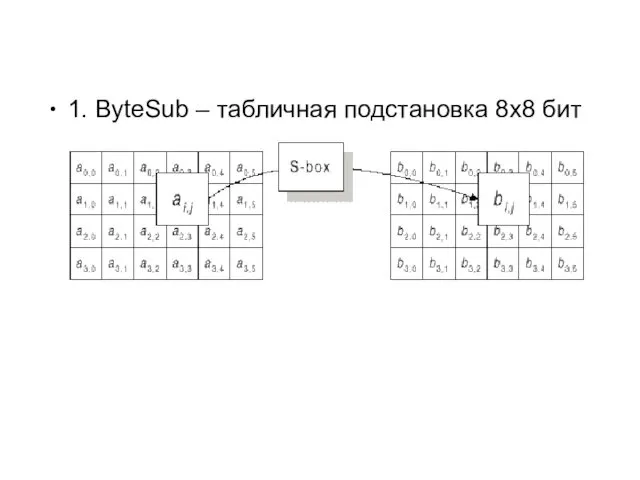
- 78. 1. ByteSub – табличная подстановка 8х8 бит
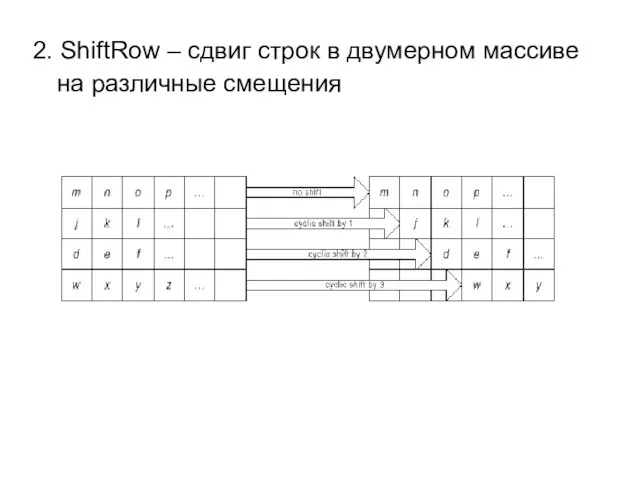
- 79. 2. ShiftRow – сдвиг строк в двумерном массиве на различные смещения
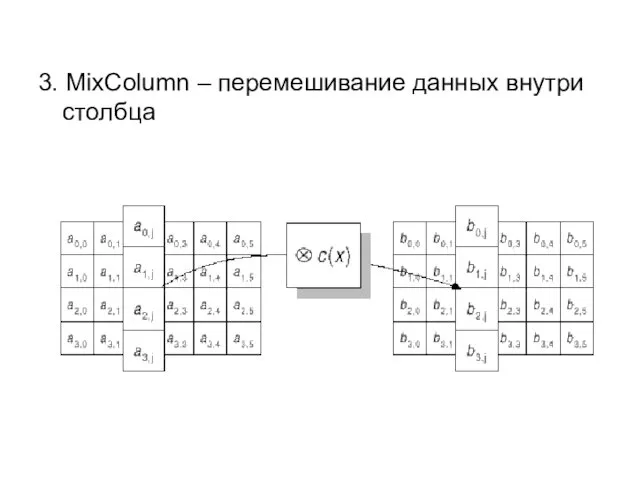
- 80. 3. MixColumn – перемешивание данных внутри столбца
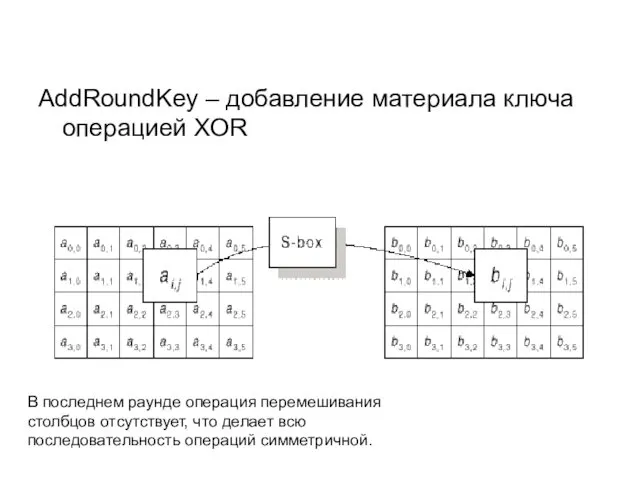
- 81. AddRoundKey – добавление материала ключа операцией XOR В последнем раунде операция перемешивания столбцов отсутствует, что делает
- 82. Криптоанализ AES На презентации алгоритма разработчики продемонстрировали атаку на 6 раундов алгоритма и заявили о необходимости
- 83. Криптоанализ Serpent Наиболее консервативный из всех участников конкурса. Полностью ориентирован на обеспечение безопасности. Наилучшая из атак
- 84. Криптоанализ Twofish Почти такой же быстрый, как AES, но с большим запасом прочности. Наилучшая атака –
- 86. Скачать презентацию

![IP: [12345678]->[26314857]. IP-1:[12345678]->[41357286]. Начальная и конечная перестановка Пример: Шифротекст:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/107956/slide-4.jpg)
![P1 :[1234]->[41232341]. P1-блок расширения: Пример.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/107956/slide-7.jpg)
![P2: [1234]->[2431]. Перестановка P2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/107956/slide-9.jpg)














































 Графический редактор Paint как инструмент для создания и обработки графики.
Графический редактор Paint как инструмент для создания и обработки графики. Електронна пошта. Передача поштових повідомлень
Електронна пошта. Передача поштових повідомлень Настройка сети Windows 7
Настройка сети Windows 7 Мы в современном медиапространстве: уважение, безопасность
Мы в современном медиапространстве: уважение, безопасность Предмет информатики. Информация, измерение, единицы измерения
Предмет информатики. Информация, измерение, единицы измерения מיון משתנים ,סולמות מדידה ,תיאור גרפי ובאמצעות מדדים
מיון משתנים ,סולמות מדידה ,תיאור גרפי ובאמצעות מדדים Презентация к занятию по внеурочной деятельности: Возникновение мультипликации
Презентация к занятию по внеурочной деятельности: Возникновение мультипликации Логические основы компьютера, 10 класс
Логические основы компьютера, 10 класс Условный оператор (Паскаль).
Условный оператор (Паскаль). Створення анімаційної сцени з використанням технології візуальних ефектів (Maya)
Створення анімаційної сцени з використанням технології візуальних ефектів (Maya) Передача информации. Локальные компьютерные сети
Передача информации. Локальные компьютерные сети Курс пользователя реестра государственных услуг. Теория
Курс пользователя реестра государственных услуг. Теория Обработка числовой информации в электронных таблицах
Обработка числовой информации в электронных таблицах Автоматизация бизнес-процессов стоматологической клиники
Автоматизация бизнес-процессов стоматологической клиники Разработка автоматизированной информационно - управляющей системы управления документооборотом кафедры АПиИТ
Разработка автоматизированной информационно - управляющей системы управления документооборотом кафедры АПиИТ Нормализация баз данных
Нормализация баз данных Computer Science 686 Spring 2007. Intel EM64T and VT Extensions
Computer Science 686 Spring 2007. Intel EM64T and VT Extensions Моделирование как метод познания
Моделирование как метод познания Технология Near Field Communication (NFC)
Технология Near Field Communication (NFC) Правовые нормы, относящиеся к информации, правонарушения в информационной сфере
Правовые нормы, относящиеся к информации, правонарушения в информационной сфере Стандарты и методология разработки корпоративных инфокоммуникационых систем
Стандарты и методология разработки корпоративных инфокоммуникационых систем Разработка автоматизированной информационной системы для учета заказов на предприятии по изготовлению корпусной мебели
Разработка автоматизированной информационной системы для учета заказов на предприятии по изготовлению корпусной мебели Relational Model
Relational Model Modelling and Simulation IS 331. Lec (7)
Modelling and Simulation IS 331. Lec (7) Информационная технология хранения данных
Информационная технология хранения данных Архитектура ЭВМ. Основные устройства компьютера
Архитектура ЭВМ. Основные устройства компьютера Арифметические основы организации ЭВМ
Арифметические основы организации ЭВМ Лавлейс Ада - тұңғыш бағдарламалаушы
Лавлейс Ада - тұңғыш бағдарламалаушы