Слайд 2

Полиномиальное хеширование
Хеш-функция сопоставляет объекту некоторое число.
Для вычисления хеша последовательности вида
a1a2a3…an нужно выбрать значение p - произвольное число большее, чем размер алфавита и mod - модуль хеширования такие, что
|ai| < p < mod, gcd(p, mod) = 1
Слайд 3

Полиномиальное хеширование
Прямой полиномиальный хеш можно вычислить следующим образом:
h = (a1 +
a2* p + a3* p2 + … + an - 1* pn - 1) % mod
Обратный полиномиальный хеш:
h = (a1 * pn - 1 + a2 * pn - 2 + … + an - 1 * p + an) % mod
Хеш вычисляется за O(N), N - длина строки.
Слайд 4

Полиномиальное хеширование
Учитывая, что хеш является значением многочлена, мы можем быстро пересчитывать
значение хеша от результата выполнения многих строковых операций.
Так для вычисления хеша подстроки произвольной длины (считается, что хеши на префиксах предпосчитаны) мы можем использовать вычитание многочленов.
Слайд 5

Полиномиальное хеширование
Пример. Дана последовательность a1a2a3a4a5. Получить значение хеша подстроки a3a4a5.
Обратный полиномиальный
хеш:
h[1:5] - h[1:2] * p3 = h[3:5]
h[1:5] = a1* p4 + a2* p3 + a3* p2 + a4* p + a5
h[1:2] = a1* p + a2
(a1* p4 + a2* p3 + a3* p2 + a4* p + a5) - (a1* p + a2)*p3 = a3* p2 + a4* p + a5
Слайд 6

Полиномиальное хеширование
Общая формула для вычисления значения хеша на подотрезке (i, j),
h(i, j) = pr[ j + 1] - pr[ i ] * p j - i + 1
Формула предподсчёта значений хеша на префиксе:
pri + 1 = pri * p + ai
Вычисление хеша на любой подстроке будет выполняться за O(1).
Слайд 7

Полиномиальное хеширование
Прямой полиномиальный хеш:
(a1 + a2* p + a3* p2 +
a4* p3 + a5* p4) - (a1 + a2* p) = a3* p2 + a4* p3 + a5* p4
Но хеш a3a4a5 равен:
a3 + a4* p + a5* p2
(a3 + a4* p + a5* p2) != (a3* p2 + a4* p3 + a5* p4)
Можно сделать так:
(a3* p2 + a4* p3 + a5* p4) * p-2
Слайд 8
![Полиномиальное хеширование В общем виде (h[ j + 1] -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/581163/slide-7.jpg)
Полиномиальное хеширование
В общем виде
(h[ j + 1] - h[ i ])
* p-i)
Для этого требуется знать обратный элемент. Если модуль выбран простым, то по теореме Эйлера мы сможем вычислить обратный элемент
pm - 2 = p-1 (mod m)
Слайд 9

Полиномиальное хеширование
Либо мы можем фиксировать не младшую степень, а старшую.
Тогда
(h[ j + 1] - h[ i ]) * pn - j
Где n - максимальный размер строки. В таком случае не требуется вычислять обратный элемент по модулю.
Слайд 10

Полиномиальное хеширование. Проверка на равенство
s = abcde → hs
t = abcde
→ ht
if (s == t) ⇒ hs == ht
if (hs == ht) ⇏ s == t
Несмотря на то, что из равенства хешей не следует равенство строк, этого можно добиться с большой вероятностью, если правильно выбрать пространство хеширования.
Выполняется за O(1)
Слайд 11

Полиномиальное хеширование. Сравнение на больше/меньше
Для сравнения на больше/меньше требуется найти первый
несовпадающий элемент слева, то есть найти минимальный префикс такой, что хеш от s и t на этом префиксе будут различны.
Находим наибольший общий префикс. Если хеши предпосчитаны, то мы можем сделать это бинарным поиском за O( log(min(len(s), len(t))) ).
Сравнить след. элемент за O(1).
Таким образом сравнение на больше/меньше выполняется за O(log(n))
Слайд 12

Полиномиальное хеширование. Уменьшение вероятности коллизий.
P = n2 / (2 * mod)
Чтобы
решение работало как можно чаще, нужно увеличить пространство хеширования.
Рассмотрим варианты, когда mod ~ 1018.
mod1 * mod2, mod1 && mod2 ∈ ℙ.
mod = 261 - 1 ∈ ℙ - самый быстрый вариант.
Также есть модуль 264 ∉ ℙ. Он удобен тем, что в C++ вычисления в типе uint64_t (unsigned long long) - вычисления по модулю 264.
Слайд 13

Полиномиальное хеширование. Строка Туэ-Морса.
При хешированию по модулю 264 строки вида
abbabaabbaababba…
В общем
виде:
Si + 1 = Si + (~Si)
Произойдёт зануление хеша.
Подробнее здесь:
https://codeforces.com/blog/entry/4898?locale=en
Слайд 14

Полиномиальное хеширование. Обмен местами двух символов в полиномиальном хеше.
Дана последовательность
s1…si…sl…sk…sj…sn
Требуется
вычислить хеш на отрезке [i, j] при условии, что sl и sk поменяли местами.
s1…[si…sk…sl…sj]…sn
Слайд 15

Полиномиальное хеширование. Обмен местами двух символов в полиномиальном хеше.
Учитывая, что у
нас были предпосчитаны хеши для начальной строки, мы можем собрать хеш новой подстроки из тех кусочков, на которых хеши не изменились:
s1…[si…sk…sl…sj]…sn
Будем считать, что мы вычислили длину не изменившихся блоков и она равна m3, m2, m1.
hm1 + sl*pm1 + hm2*pm1 + 1 + sk*pm1 + 1 + m2 + hm3*pm1 + m2 + 2
Слайд 16

Полиномиальное хеширование. Применение
Поиск всех вхождений одной строки длины n в другую
длины m за O(n + m)
Поиск наибольшей общей подстроки двух строк длин n и m (n ≥ m) за O((n + m·log(n))·log(m)) и O(n·log(m))
Нахождение лексикографически минимального циклического сдвига строки длины n за O(n·log(n))
Сортировка всех циклических сдвигов строки длины n в лексикографическом порядке за O(n·log(n)2)
Нахождение количества подпалиндромов строки длины n за O(n·log(n))
Количество подстрок строки длины n, являющихся циклическими сдвигами строки длины m за O((n + m)·log(n))
Количество суффиксов строки длины n, бесконечное расширение которых совпадает с бесконечным расширением всей строки за O(n·log(n)) (расширение — дублирование строки бесконечное число раз)
Наибольший общий префикс двух строк длины n с обменом двух произвольных символов одной строки местами за O(n·log(n))
Слайд 17

Полиномиальное хеширование. Полезные ссылки
https://codeforces.com/blog/entry/65819 - вычисление по модулю 261 - 1
https://pastebin.com/5Run2F5y
- реализация хеша в виде структуры данных
https://e-maxx.ru/algo/string_hashes
https://codeforces.com/blog/entry/60445
Слайд 18

Z-функция строки
Z-функция - массив длины n, i-ый элемент которого равен наибольшему
числу символов, начиная с позиции i, совпадающих с первыми символами строки S.
Иными словами Z[ i ] - это наибольший общий префикс строки S и её i-того суффикса.
Первый элемент Z-функции, Z[0] обычно считается неопределённым.
Слайд 19

Z-функция. Тривиальный алгоритм
Простая реализация выполняется за O(N2), где N - длина
строки. Для каждой позиции i перебираем для неё ответ, пока не обнаружим несовпадение или не дойдём до конца строки.
vector zFunction(s : string):
vector zf(n);
for i = 1 to n − 1
while i + zf[i] < n and s[zf[i]] == s[i + zf[i]]
zf[i]++
return zf
Слайд 20

Z-функция. Эффективный алгоритм
Назовём Z-блоком подстроку с началом в позиции i и
длиной Z[ i ]. Заведём 2 переменные: left и right - начало и конец Z-блока строки S, с максимальной позицией конца right. Изначально left = 0, right = 0.
i > right: Пробегаем по строке S и сравниваем символы на позициях S[i +j] и S[ j ]. Пусть j первая позиция для которой не выполняется S[i +j] = S[ j ]. Тогда j это и Z-функция для позиции i. Тогда left = i, right = i + j - 1
i <= right: Сравним Z[i - left] + i и right. Если right <, то нужно наивно пробежаться по строке начиная с позиции right и вычислить Z[ i ]. Иначе мы уже знаем верное значение Z[ i ], т.к. оно равно Z[ i - left ].
Этот алгоритм работает за O(N), N - длина строки
Слайд 21

Z-функция. Ссылки
https://e-maxx.ru/algo/z_function - тут есть доказательство линейности алгоритма
https://neerc.ifmo.ru/wiki/index.php?title=Z-функция
Слайд 22
![Префикс-функция Дана строка s[0…n-1]. Требуется вычислить для неё префикс-функцию, т.е.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/581163/slide-21.jpg)
Префикс-функция
Дана строка s[0…n-1]. Требуется вычислить для неё префикс-функцию, т.е. массив чисел
π[0…n-1], где π[ i ] определяется как наибольшая длина наибольшего собственного суффикса подстроки s[0…i], совпадающего с её префиксом.
Значение π[0] полагается равным 0.
Слайд 23
![Префикс-функция. Эффективный алгоритм Заметим, что p[i+1] Избавимся от явных сравнений](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/581163/slide-22.jpg)
Префикс-функция. Эффективный алгоритм
Заметим, что p[i+1] <= p[i]+1. Чтобы показать это, рассмотрим
суффикс,оканчивающийся на позиции i+1 и имеющий длину p[i+1], удалив из него последний символ, мы получим суффикс, оканчивающийся на позиции i и имеющий длину p[i + 1] - 1.
Избавимся от явных сравнений строк. Пусть мы вычислили p[i], тогда, если s[i+1]=s[p[i]], то p[i+1]=p[i]+1. Если окажется, что s[i+1]≠s[p[i]], то нужно попытаться попробовать подстроку меньшей длины. Хотелось бы сразу перейти к такому бордеру наибольшей длины, для этого подберем такое k, что k=p[i]−1. Делаем это следующим образом. За исходное k необходимо взять p[i−1], что следует из первого пункта. В случае, когда символы s[k] и s[i] не совпадают, p[k−1] — следующее потенциальное наибольшее значение k, что видно из рисунка. Последнее утверждение верно, пока k>0, что позволит всегда найти его следующее значение. Если k=0, то p[i]=1 при s[i]=s[1] , иначе p[i]=0.
Время работы алгоритма составит O(n).
Слайд 24

Алгоритм Кнута-Морриса-Пратта
КМП предназначен для поиска шаблона (подстроки) в строке.
https://leetcode.com/problems/find-the-index-of-the-first-occurrence-in-a-string/
Слайд 25

Префикс-функция → Z-функция & V/V ~ O(N)
Префикс-функция и Z-функция взаимозаменяемы и
могут быть представлены друг через друга за линейное время.
https://clck.ru/32jg2N - Построение префикс-функции по Z-функции
https://clck.ru/D3niW - Построение Z-функции по префикс-функции






![Полиномиальное хеширование В общем виде (h[ j + 1] -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/581163/slide-7.jpg)













![Префикс-функция Дана строка s[0…n-1]. Требуется вычислить для неё префикс-функцию, т.е.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/581163/slide-21.jpg)
![Префикс-функция. Эффективный алгоритм Заметим, что p[i+1] Избавимся от явных сравнений](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/581163/slide-22.jpg)


 Электронные таблицы Excel
Электронные таблицы Excel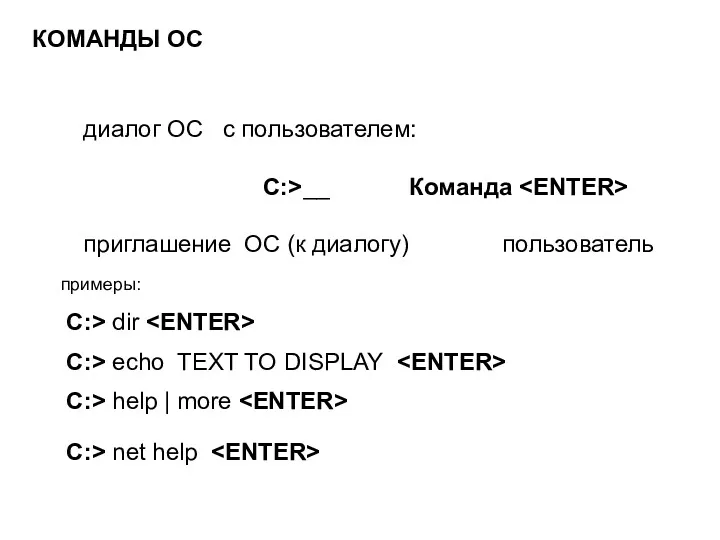 Команды ОС. Диалог ОС с пользователем
Команды ОС. Диалог ОС с пользователем Двоичное кодирование текстовой информации
Двоичное кодирование текстовой информации Функции VBA
Функции VBA Введение в курс информатики и ИКТ. (8 класс)
Введение в курс информатики и ИКТ. (8 класс)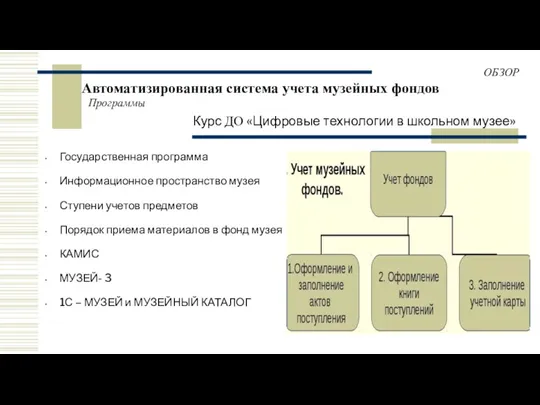 Автоматизированная система учета музейных фондов
Автоматизированная система учета музейных фондов Устройства ввода
Устройства ввода Инновационные технологии в журналистике
Инновационные технологии в журналистике Gadgets or new technologies in our life
Gadgets or new technologies in our life Занимательные задачки по информатике
Занимательные задачки по информатике Сетевые операционные системы
Сетевые операционные системы Файлы и папки
Файлы и папки Процедуры и функции в Паскале
Процедуры и функции в Паскале Мектеп сайтын жасау әдістемесі
Мектеп сайтын жасау әдістемесі ПрезентацияПоGpss №10
ПрезентацияПоGpss №10 Графический интерфейс в Python
Графический интерфейс в Python Мультимедийнная презентация у уроку информатики на тему Основы логики
Мультимедийнная презентация у уроку информатики на тему Основы логики Кодирование и обработка графической информации
Кодирование и обработка графической информации Объединение компьютеров в локальную сеть Организация работы пользователей в локальных компьютерных сетях
Объединение компьютеров в локальную сеть Организация работы пользователей в локальных компьютерных сетях Конспекты уроков 10 класс (1 четверть)
Конспекты уроков 10 класс (1 четверть) Презентация Использование ЦОР и ЭОР в учебном процессе
Презентация Использование ЦОР и ЭОР в учебном процессе ITK Lecture 6 - The Pipeline
ITK Lecture 6 - The Pipeline Устройства ввода информации. (7класс)
Устройства ввода информации. (7класс) Анализ современных подходов к разработке мобильных приложений на примере приложения: Дневник стрелка
Анализ современных подходов к разработке мобильных приложений на примере приложения: Дневник стрелка TNS Web Index. Аудитория интернет-проектов. Результаты исследования: Апрель 2016
TNS Web Index. Аудитория интернет-проектов. Результаты исследования: Апрель 2016 Виртуальная реальность
Виртуальная реальность Презентация по информатике для 8 класса Виды информации
Презентация по информатике для 8 класса Виды информации Интернет-банк РНКБ
Интернет-банк РНКБ