Содержание
- 2. Алгоритм всегда рассчитан на выполнение «неразмышляющим» исполнителем. Алгоритм не содержит ошибок, если он дает правильные результаты
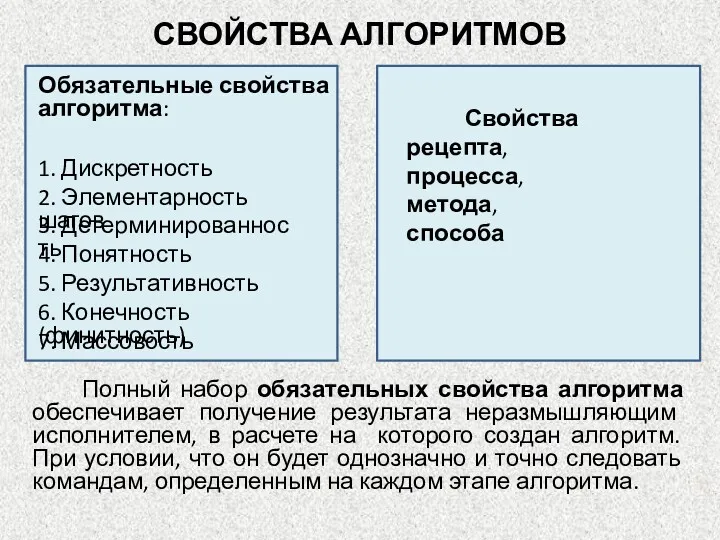
- 3. СВОЙСТВА АЛГОРИТМОВ Полный набор обязательных свойства алгоритма обеспечивает получение результата неразмышляющим исполнителем, в расчете на которого
- 4. • Получить решение поставленной задачи нередко можно разными способами, привлекая разные алгоритмы. • Как выбрать наиболее
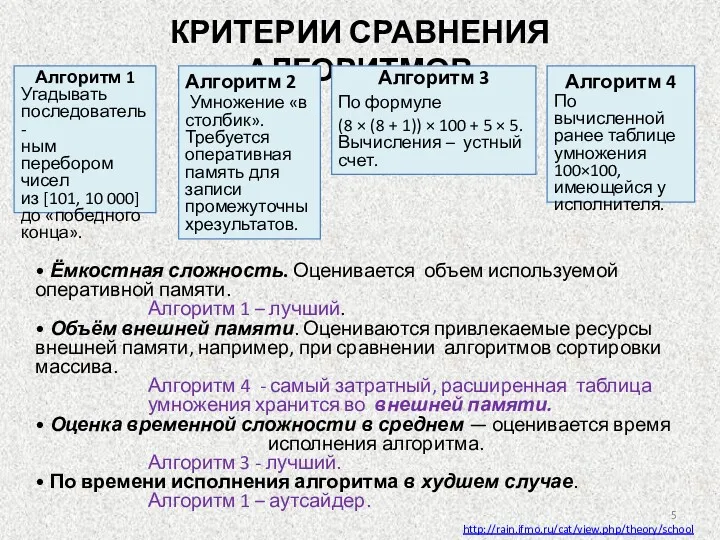
- 5. • Ёмкостная сложность. Оценивается объем используемой оперативной памяти. Алгоритм 1 – лучший. • Объём внешней памяти.
- 6. • Оценивать эффективность компьютерного алгоритма следует до написания и отладки компьютерной программы. • Нередко оценка временной
- 7. 1. Могилев А.В. Информатика / А. В. Могилев, Н. И. Пак, Е. К. Хеннер. — М.:
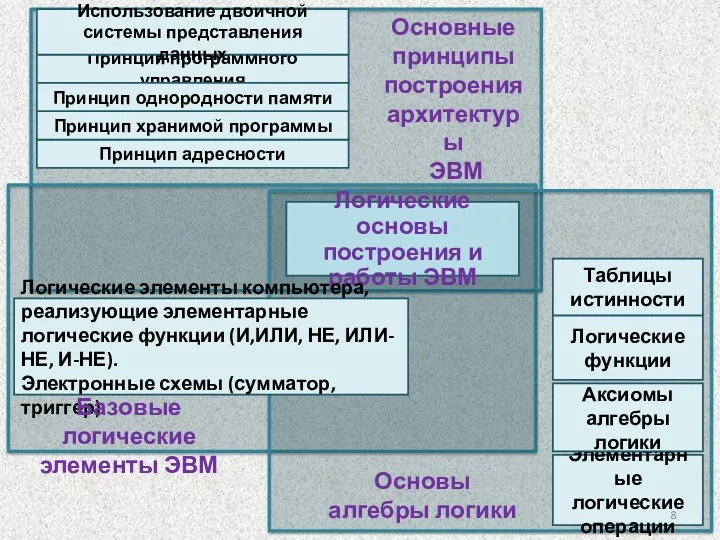
- 8. Таблицы истинности Логические основы построения и работы ЭВМ Принцип программного управления Логические элементы компьютера, реализующие элементарные
- 9. Логика – наука о формах и способах мышления Законы логики отражают в сознании человека свойства, связи
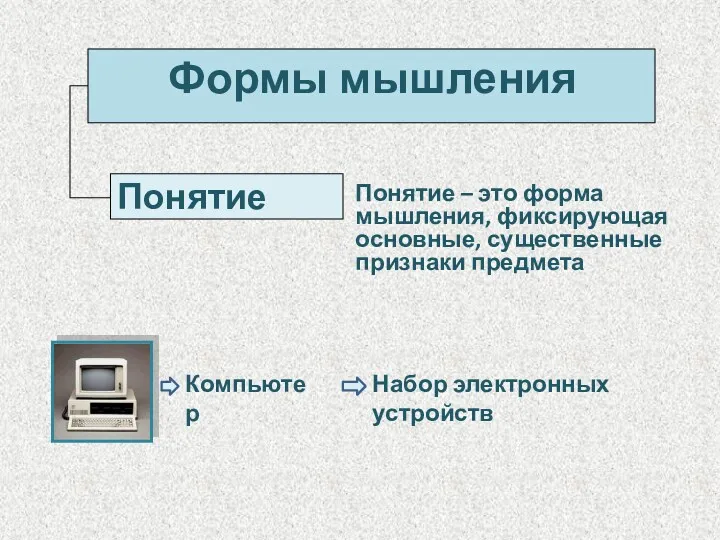
- 10. Понятие Понятие – это форма мышления, фиксирующая основные, существенные признаки предмета
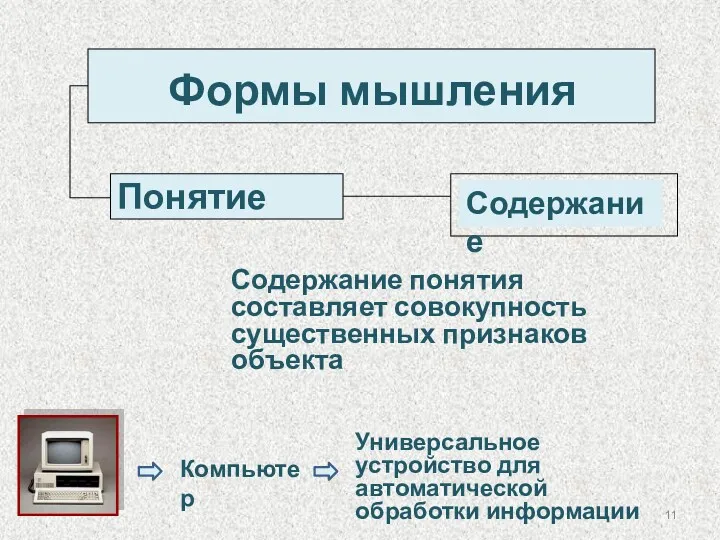
- 11. Формы мышления Понятие Содержание понятия составляет совокупность существенных признаков объекта Универсальное устройство для автоматической обработки информации
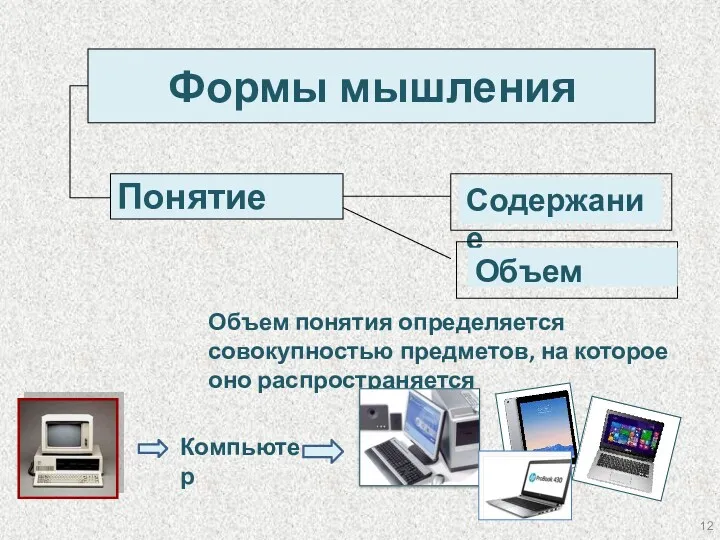
- 12. Формы мышления Понятие Объем понятия определяется совокупностью предметов, на которое оно распространяется Компьютер
- 13. Формы мышления Понятие Высказывание 2 х 2 =4 - математический язык Дважды два равно пять –
- 14. Формы мышления Понятие Высказывание Все углы треугольника равны Треугольник равносторонний Умозаключение – это форма мышления, с
- 15. Высказывание принимает одно из двух значений: (1) истина, (0) – ложь Алгебра высказываний служит для определения
- 16. Составное высказывание содержит высказывания, объединенные логическими операциями. Пример. Составное высказывание, состоящее из двух простых, соединённых союзом
- 17. Логическое умножение (конъюнкция) - объединение двух или более высказываний в одно при помощи операции «И». Конъюнкция
- 18. Логическое умножение (конъюнкция) Пример 1. На улице идет дождь На улице светит солнце Стоит теплая погода
- 19. Логическое сложение (дизъюнкция)- объединение двух или более высказываний в одно при помощи союза «ИЛИ» Дизъюнкция обозначается:
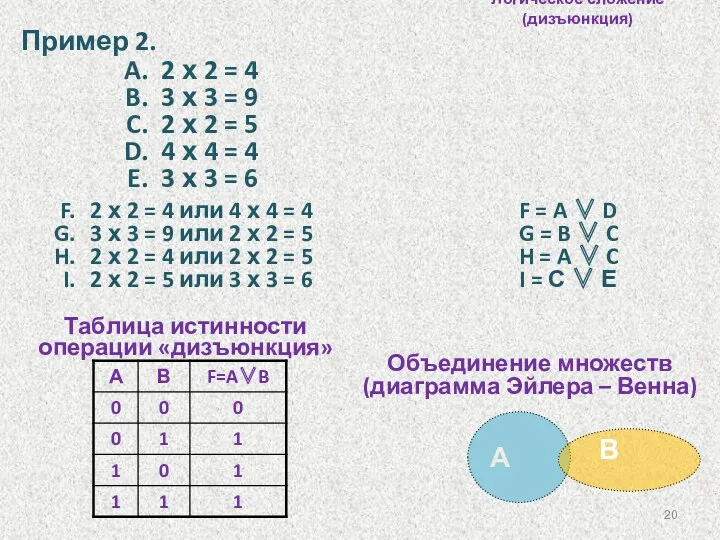
- 20. Логическое сложение (дизъюнкция) Пример 2. 2 х 2 = 4 3 х 3 = 9 2
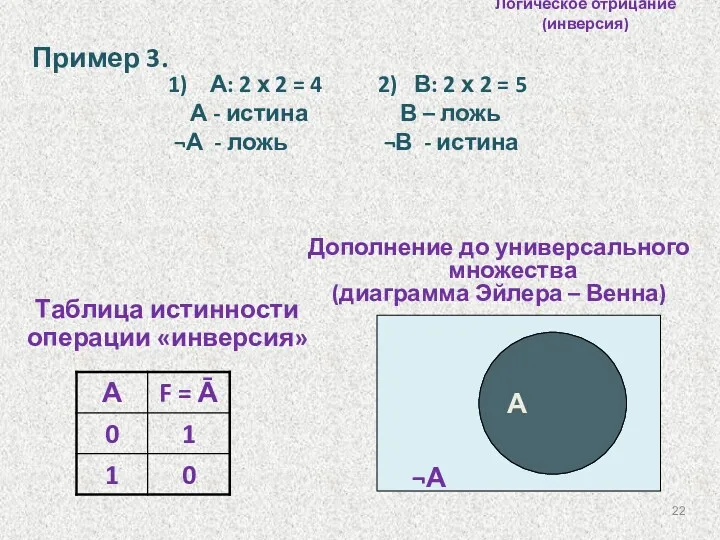
- 21. Логическое отрицание (инверсия) – присоединение частицы «не» к высказыванию Инверсия обозначается: ‾, ¬ Логическое отрицание (инверсия)
- 22. Логическое отрицание (инверсия) Пример 3. 2) В: 2 х 2 = 5 В – ложь ¬В
- 23. Импликация двух высказываний A и B - такое высказывание, которое ложно тогда и только тогда, когда
- 24. Эквиваленция двух высказываний A и B - такое высказывание, которое истинно тогда и только тогда, когда
- 25. Логической переменной называется переменная, значением которой может быть любое высказывание, например: x, у, x1, y1, xk,
- 26. Формулы А и B, зависящие от одного и того же набора переменных x1, х2, х3, …
- 27. ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ действия в скобках инверсия конъюнкция дизъюнкция импликация эквивалентность Пример. U ∨ (В ⇒
- 28. Пример 5. Даны простые высказывания: A: Процессор – устройство для обработки информации B: Сканер – устройство
- 29. Логические выражения и таблицы истинности Таблица истинности определяет истинность или ложность высказывания (логического выражения) при всех
- 30. ЛОГИЧЕСКИЕ ФУНКЦИИ Любое составное высказывание можно рассматривать как логическую функцию F(X1, X2, …, XN), аргументами которой
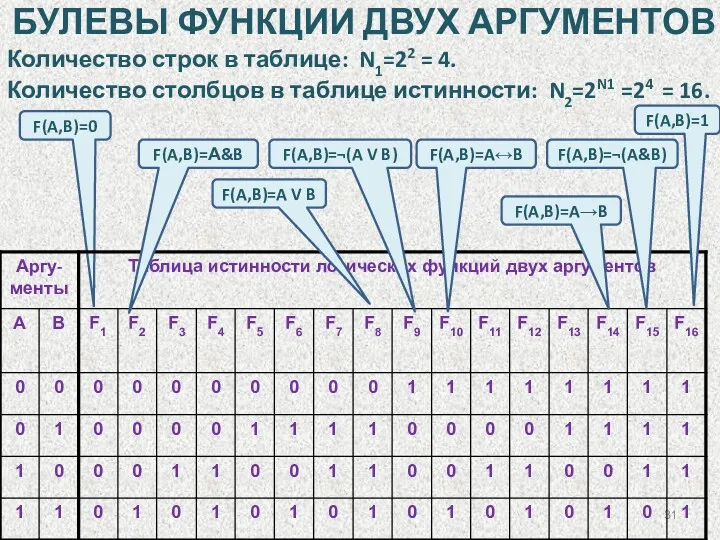
- 31. F(A,B)=0 БУЛЕВЫ ФУНКЦИИ ДВУХ АРГУМЕНТОВ Количество строк в таблице: N1=22 = 4. Количество столбцов в таблице
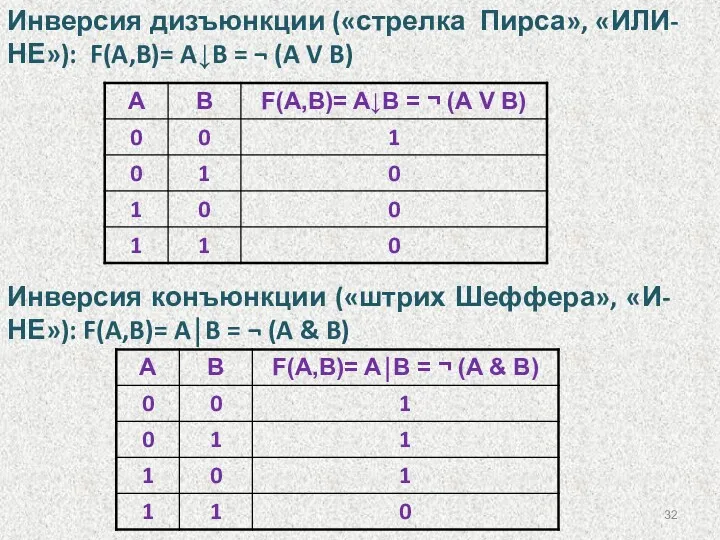
- 32. Инверсия дизъюнкции («стрелка Пирса», «ИЛИ-НЕ»): F(A,B)= A↓B = ¬ (A V B) Инверсия конъюнкции («штрих Шеффера»,
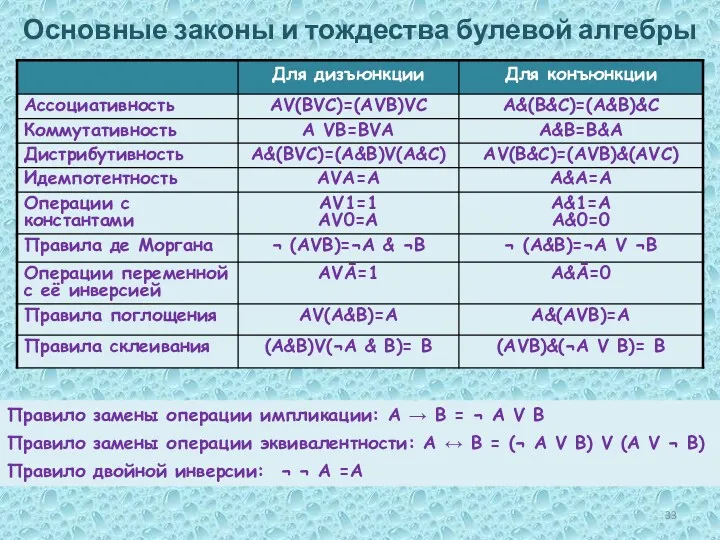
- 33. Основные законы и тождества булевой алгебры Правило замены операции импликации: A → B = ¬ A
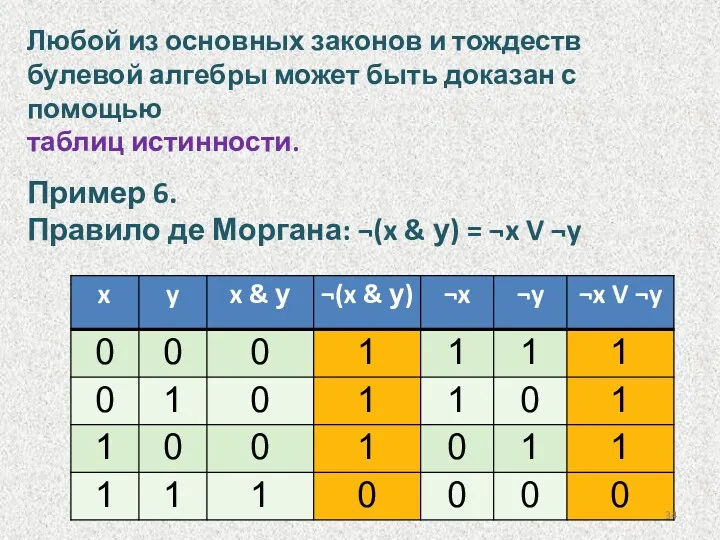
- 34. Любой из основных законов и тождеств булевой алгебры может быть доказан с помощью таблиц истинности. Пример
- 35. Законы алгебры логики можно доказать путем логических рассуждений. Пример 7. Доказательство первого закона поглощения: x V
- 36. Законы алгебры логики можно доказать путем тождественных преобразований. Пример 8. Доказательство первого закона поглощения x v
- 37. Формула А называется тавтологией (или тождественно истинной), если она истинна при любых значениях своих переменных. Пример
- 38. Формула А называется тождественно ложной, если она равна 0 при любых значениях своих переменных. Пример 10.
- 39. Пример 11. Определить x, если: ¬(x V a) V ¬(x V ¬a) = b ¬(x V
- 40. Пример 12. Какие формулы являются тавтологиями? ¬(a & ¬a) a → (b → a) (a &
- 41. 1) ¬(a & ¬a)
- 42. 2) a → (b → a)
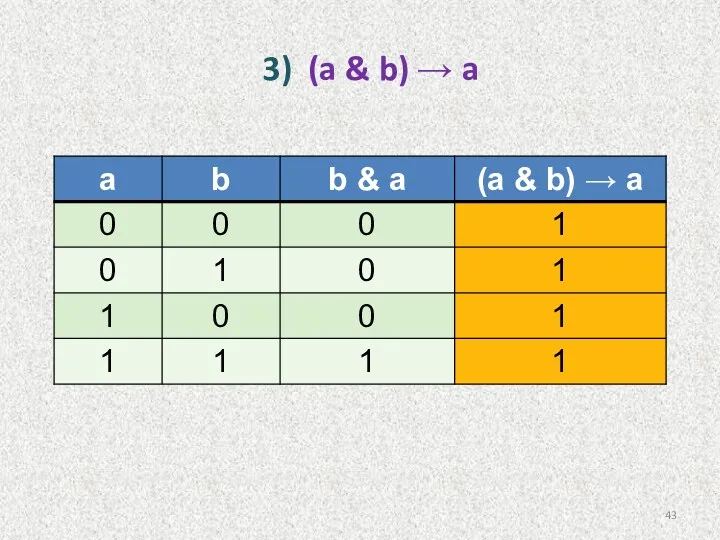
- 43. 3) (a & b) → a
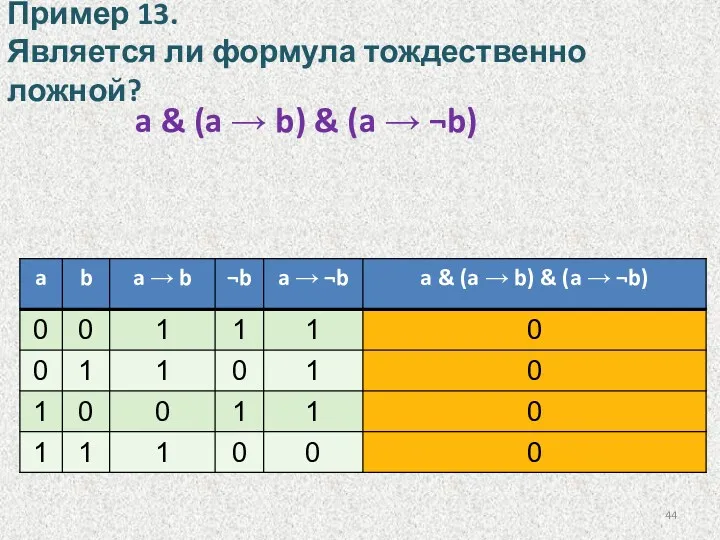
- 44. Пример 13. Является ли формула тождественно ложной? a & (a → b) & (a → ¬b)
- 45. Пример 14. Упростить: Любую формулу можно преобразовать к равносильной ей, в которой используются только операции НЕ,
- 46. Пример 15. Способ 1. Применим закон дистрибутивности: Способ 2. Перемножим скобки на основании закона дистрибутивности:
- 47. F1 = {если одно слагаемое делится на 3 и сумма делится на 3, то и другое
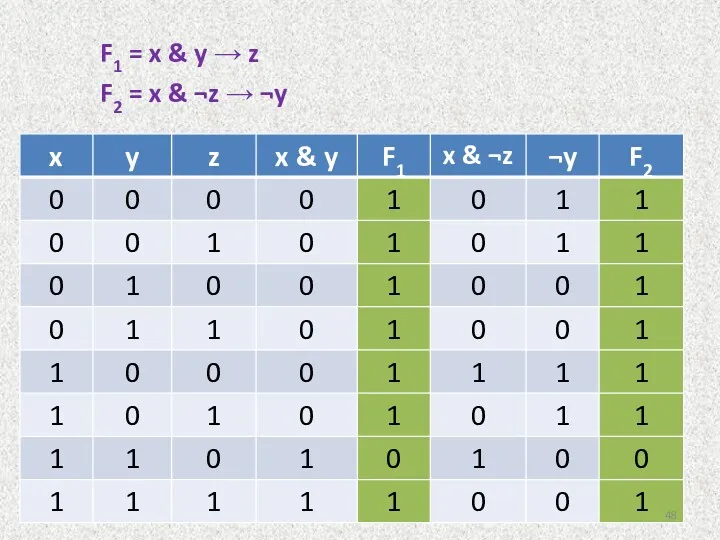
- 48. F1 = x & y → z F2 = x & ¬z → ¬y
- 49. Решение логических задач Выделить из условия задачи элементарные высказывания и обозначить их буквами. Записать условие задачи
- 50. Пример 17. На вопрос «Кто из трех студентов изучал логику?», был получен ответ: «Если изучал первый,
- 51. Логику изучал третий учащийся, а первый и второй не изучали. Обозначим: Р1 – , Р2 –
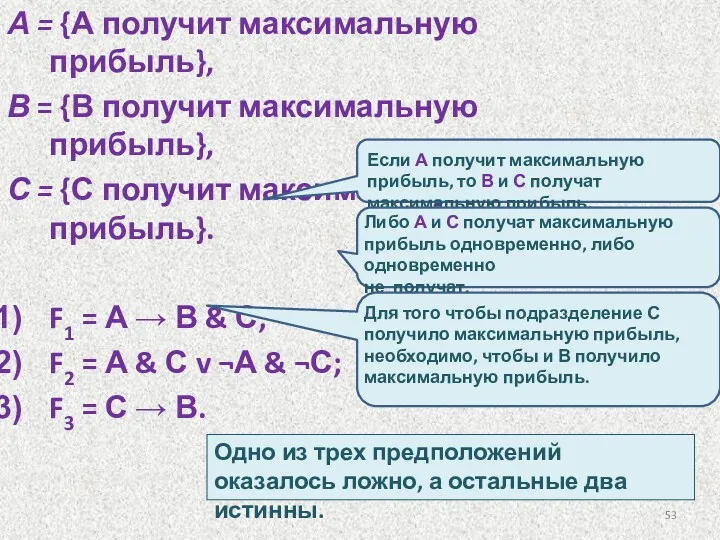
- 52. Пример 18. Три подразделения А, В, С фирмы стремились получить максимальную прибыль. Если А получит максимальную
- 53. А = {А получит максимальную прибыль}, В = {В получит максимальную прибыль}, С = {С получит
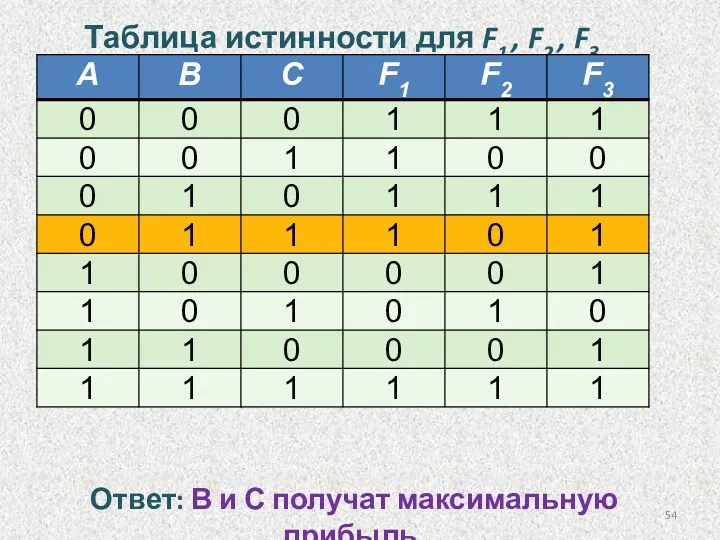
- 54. Таблица истинности для F1 , F2 , F3 Ответ: В и С получат максимальную прибыль.
- 56. Скачать презентацию



































 Стек протоколов TCP/IP
Стек протоколов TCP/IP Контейнеры. Векторы
Контейнеры. Векторы Корпоративные информационные системы
Корпоративные информационные системы Преступления в сети
Преступления в сети Поколения ЭВМ
Поколения ЭВМ Сокращение размерности пространства признаков при классификации
Сокращение размерности пространства признаков при классификации Excel и его объекты
Excel и его объекты С++ бағдарламалау тілі
С++ бағдарламалау тілі Создание личного кабинета на сайте Avon
Создание личного кабинета на сайте Avon Основы языка VB Урок 3: Функции
Основы языка VB Урок 3: Функции Устройство компьютера (10 класс)
Устройство компьютера (10 класс) 1С: Медицина. Больничная аптека 2.1 Поддержка ФГИС МДЛП
1С: Медицина. Больничная аптека 2.1 Поддержка ФГИС МДЛП Интеллектуалды жүйелер. Білім негізінде қазіргі кезде жобалау және интеллектуалды жүйелерді өңдеу
Интеллектуалды жүйелер. Білім негізінде қазіргі кезде жобалау және интеллектуалды жүйелерді өңдеу Языки и системы программирования
Языки и системы программирования Оформление цитат, списка литературы, библиографических ссылок
Оформление цитат, списка литературы, библиографических ссылок Платформы для дистанционного обучения
Платформы для дистанционного обучения Работа в научной электронной библиотеке eLibrary
Работа в научной электронной библиотеке eLibrary Modbus Plus
Modbus Plus Нейронные сети глубокого обучения
Нейронные сети глубокого обучения Контент-стратегии цифровой журналистики
Контент-стратегии цифровой журналистики История развития операционной системы Windows
История развития операционной системы Windows Универсальные поисковые системы
Универсальные поисковые системы Урок информатики и ИКТ в 7 классе по теме Сложные таблицы (УМК Л.Л.Босова)
Урок информатики и ИКТ в 7 классе по теме Сложные таблицы (УМК Л.Л.Босова) LDI Plus Presentation EN
LDI Plus Presentation EN Работа с базами данных научных публикаций
Работа с базами данных научных публикаций Информационно-справочная документация и её оформление
Информационно-справочная документация и её оформление База данных
База данных Системное программное обеспечение. Операционные системы
Системное программное обеспечение. Операционные системы