Слайд 2

Слайд 3
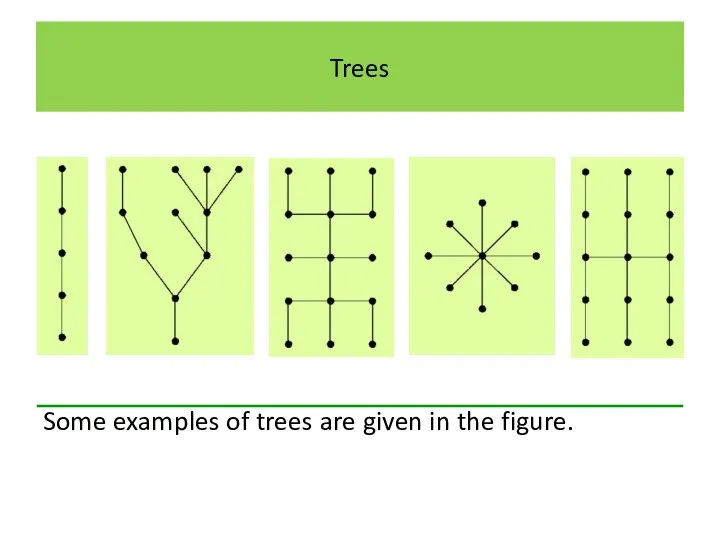
Trees
Some examples of trees are given in the figure.
Слайд 4

Слайд 5
Слайд 6

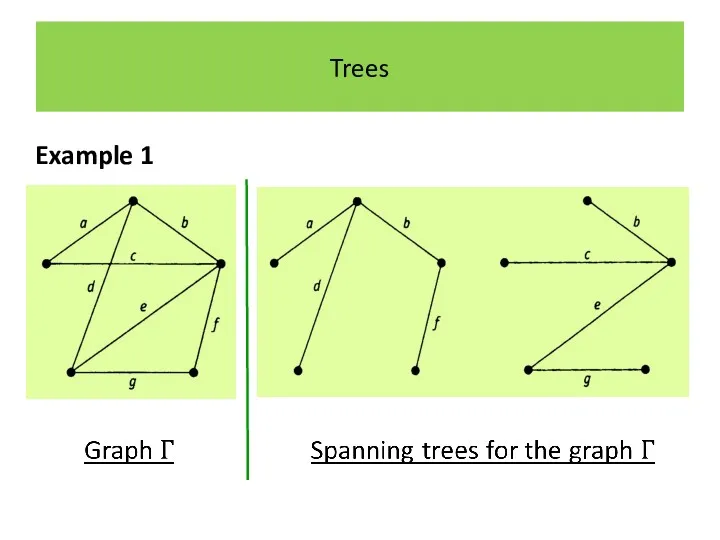
Trees
Theorem 1
Every connected graph contains a spanning tree.
Слайд 7

? Every connected graph contains a spanning tree.
Proof
Слайд 8

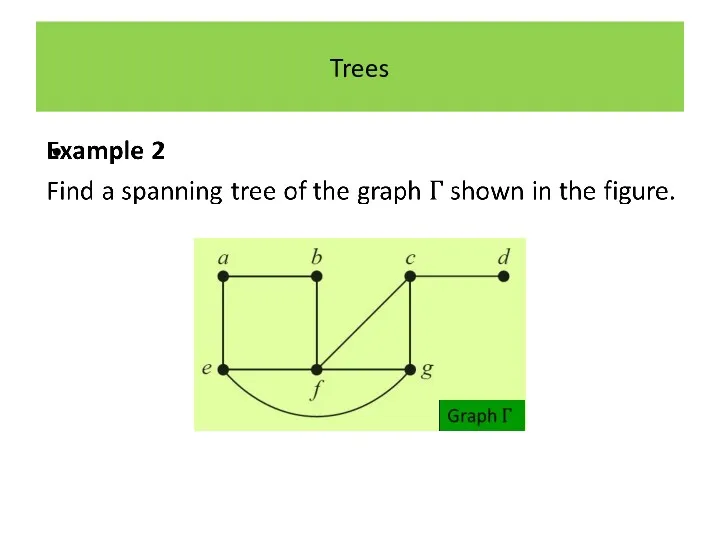
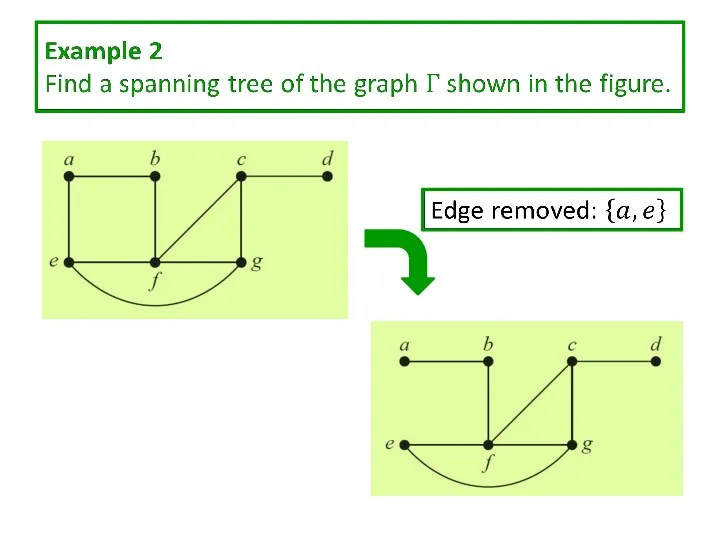
? Every connected graph contains a spanning tree.
Proof
Слайд 9
Слайд 10
Слайд 11
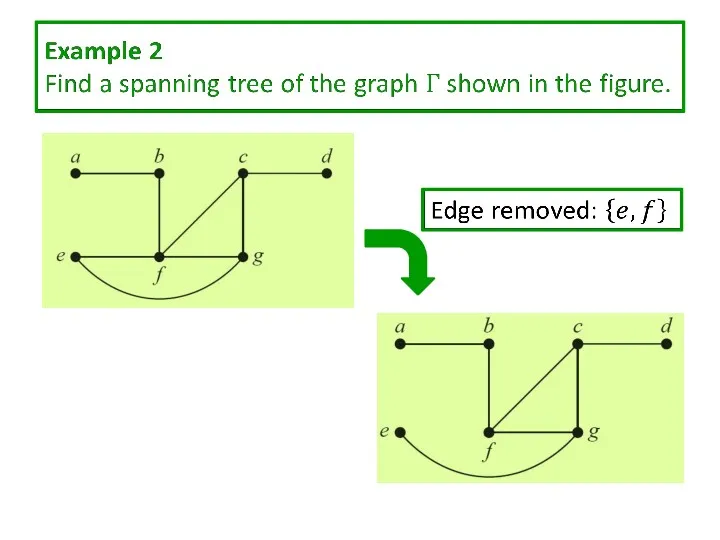
Слайд 12
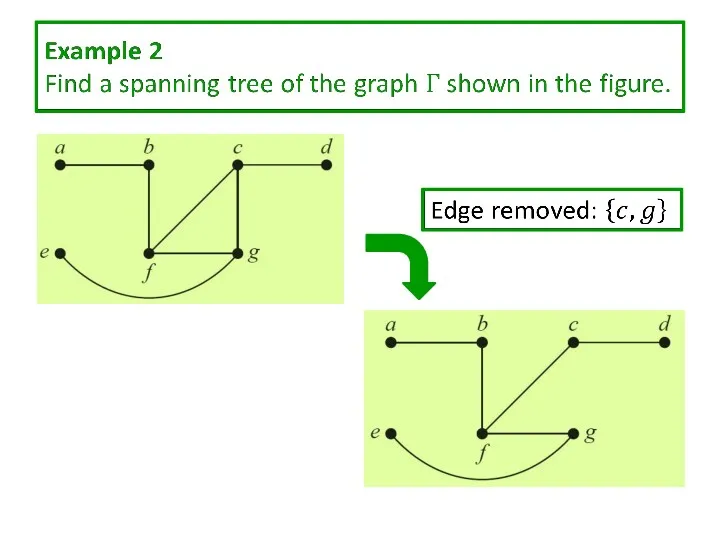
Слайд 13
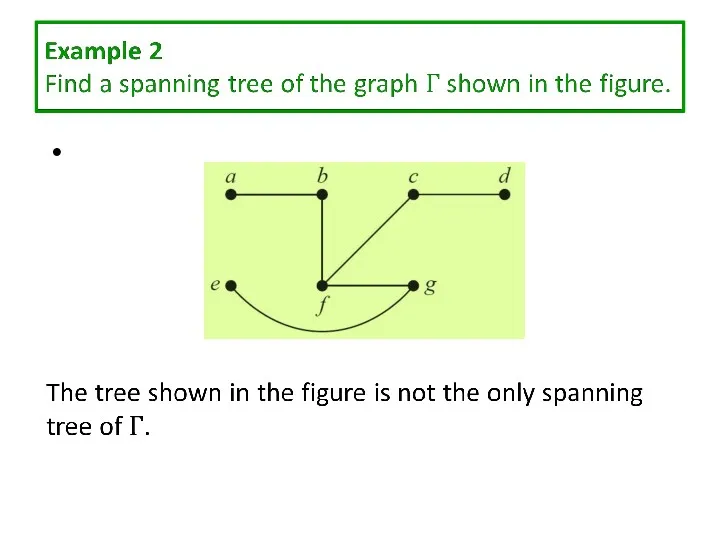
Слайд 14
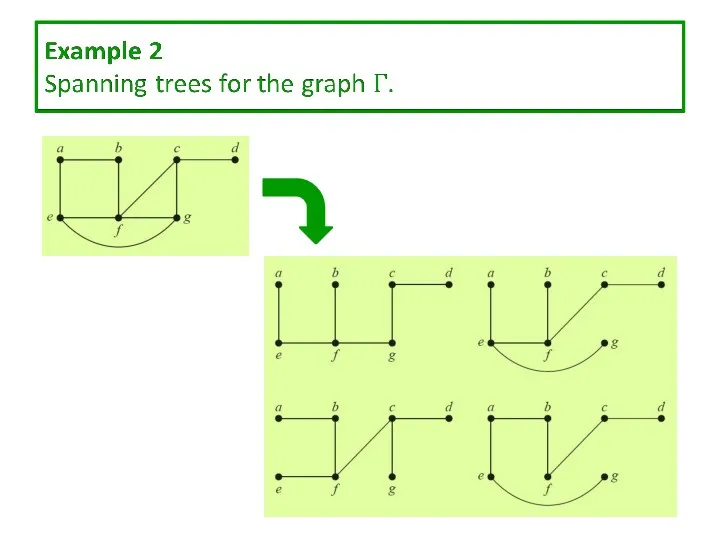
Слайд 15

Trees
Definition 3
A forest is a (not necessarily connected) graph each of
whose components is a tree.
Слайд 16
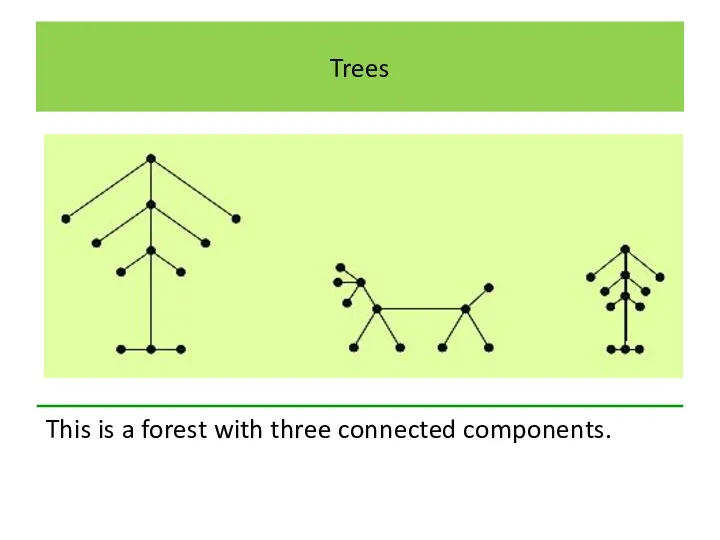
Trees
This is a forest with three connected components.
Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

Слайд 25

Слайд 26

Слайд 27

Слайд 28
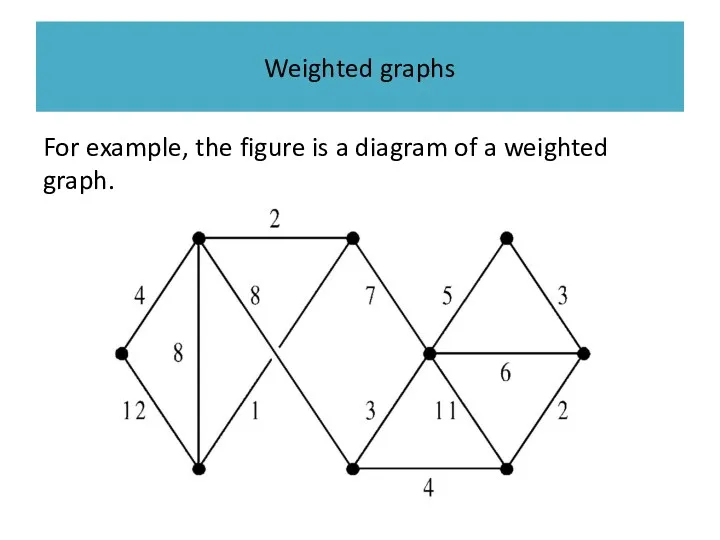
Weighted graphs
For example, the figure is a diagram of a weighted
graph.
Слайд 29

Слайд 30

Слайд 31

Слайд 32

Weighted graphs
The figure shows a weighted graph with two minimal spanning
trees, both of weight 22.
Слайд 33

An algorithm which produces a minimal spanning tree (Prim’s algorithm)
Слайд 34
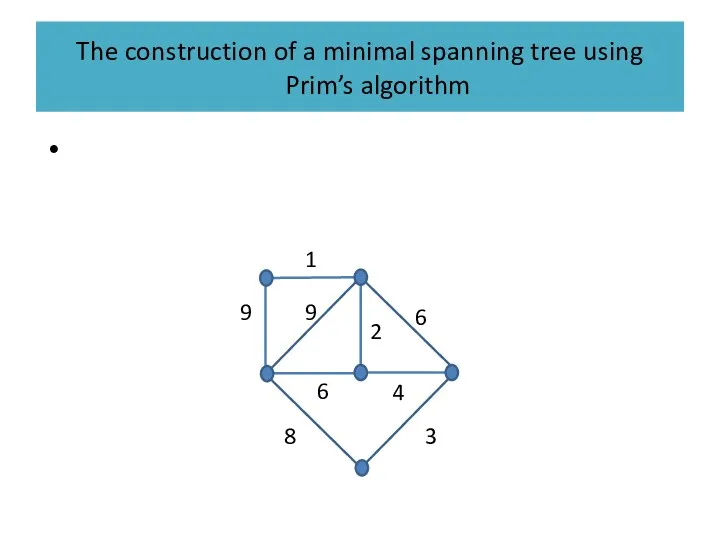
The construction of a minimal spanning tree using Prim’s algorithm
1
9
2
6
3
8
6
4
9
Слайд 35
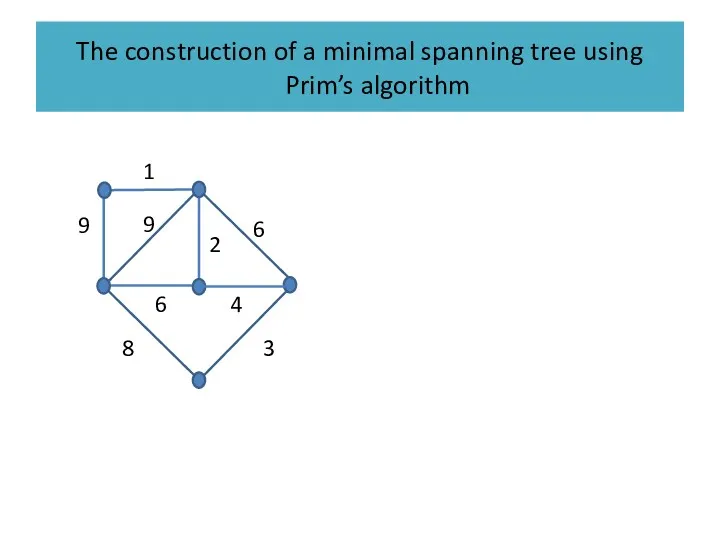
The construction of a minimal spanning tree using Prim’s algorithm
1
9
2
6
3
8
6
4
9
1
9
2
6
3
8
6
4
9
Слайд 36
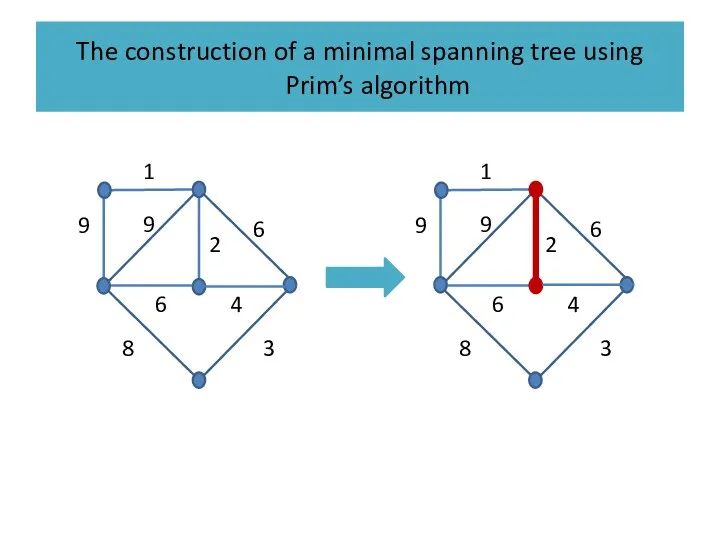
The construction of a minimal spanning tree using Prim’s algorithm
1
9
2
6
3
8
6
4
9
1
9
2
6
3
8
6
4
9
Слайд 37
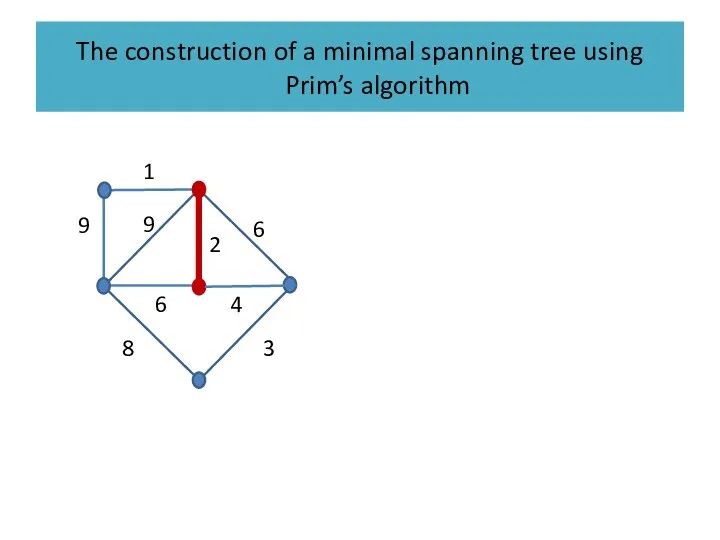
The construction of a minimal spanning tree using Prim’s algorithm
1
9
2
6
3
8
6
4
9
1
9
2
6
3
8
6
4
9
Слайд 38
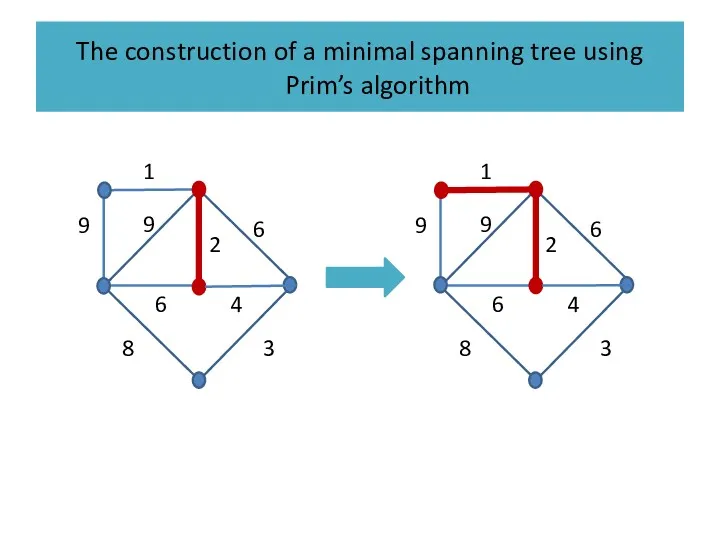
The construction of a minimal spanning tree using Prim’s algorithm
1
9
2
6
3
8
6
4
9
1
9
2
6
3
8
6
4
9
Слайд 39
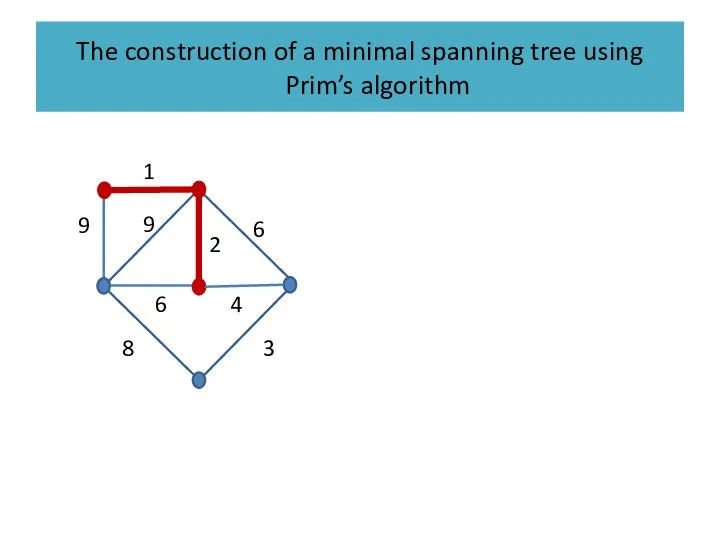
The construction of a minimal spanning tree using Prim’s algorithm
1
9
2
6
3
8
6
4
9
1
9
2
6
3
8
6
4
9
Слайд 40

The construction of a minimal spanning tree using Prim’s algorithm
1
9
2
6
3
8
6
4
9
1
9
2
6
3
8
6
4
9
Слайд 41
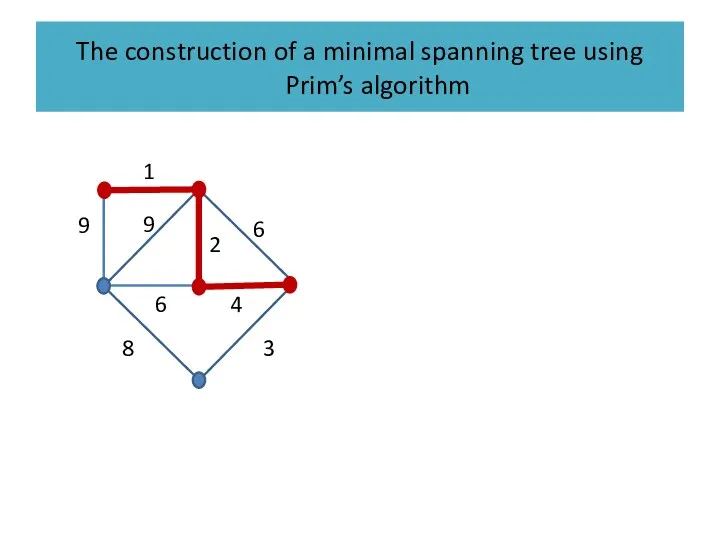
The construction of a minimal spanning tree using Prim’s algorithm
1
9
2
6
3
8
6
4
9
1
9
2
6
3
8
6
4
9
Слайд 42
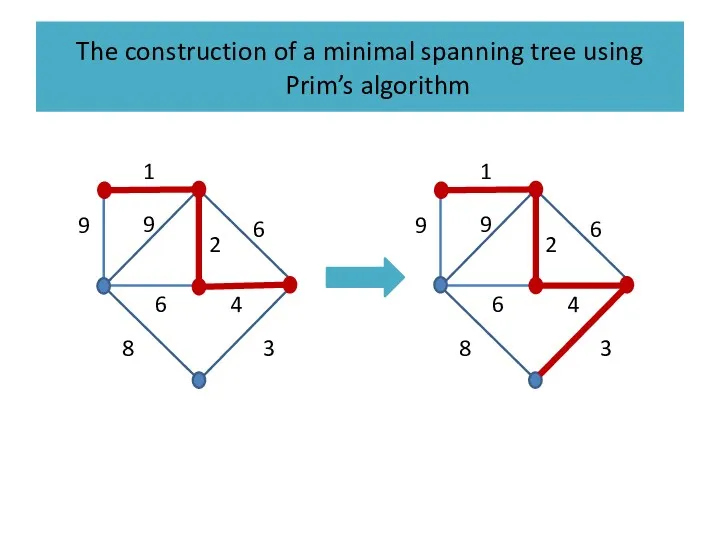
The construction of a minimal spanning tree using Prim’s algorithm
1
9
2
6
3
8
6
4
9
1
9
2
6
3
8
6
4
9
Слайд 43
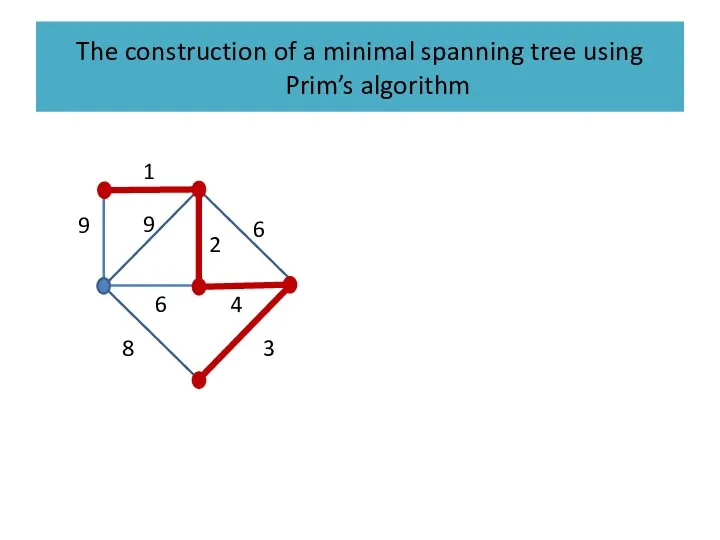
The construction of a minimal spanning tree using Prim’s algorithm
1
9
2
6
3
8
6
4
9
1
9
2
6
3
8
6
4
9
Слайд 44
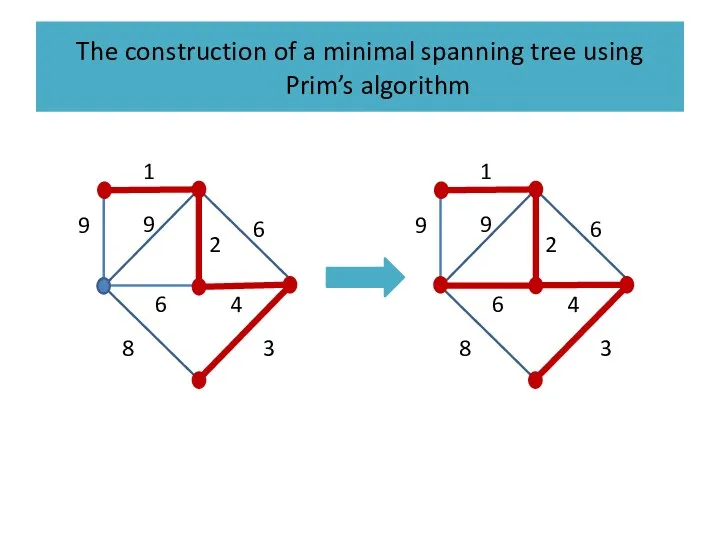
The construction of a minimal spanning tree using Prim’s algorithm
1
9
2
6
3
8
6
4
9
1
9
2
6
3
8
6
4
9
Слайд 45
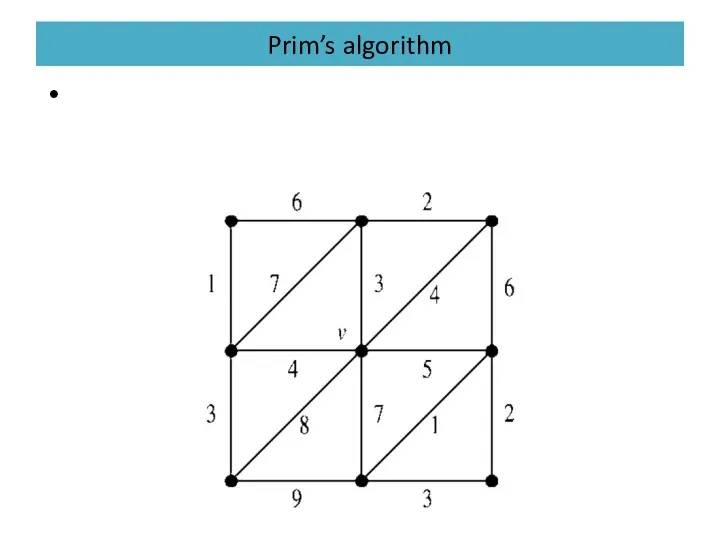
Слайд 46

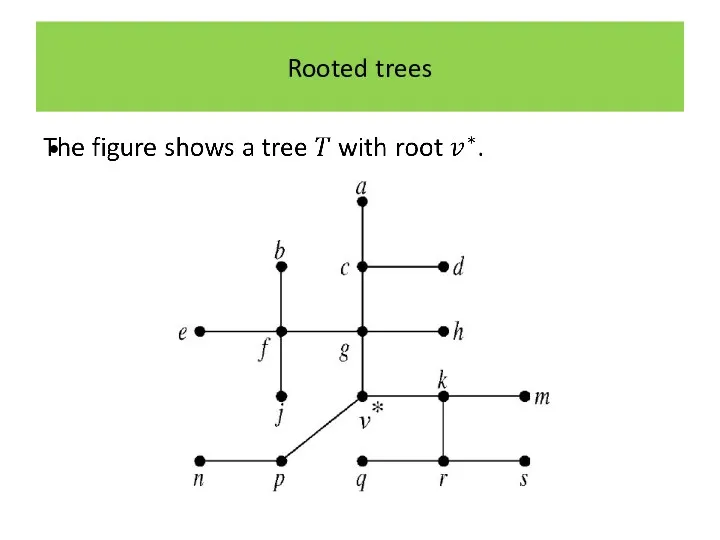
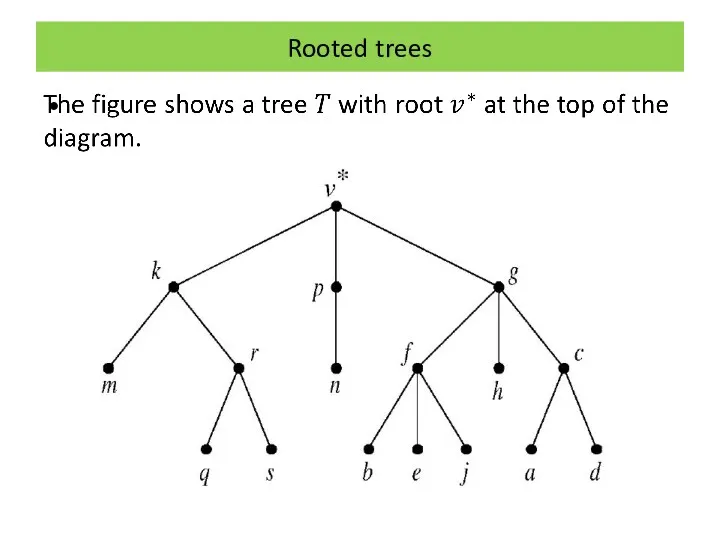
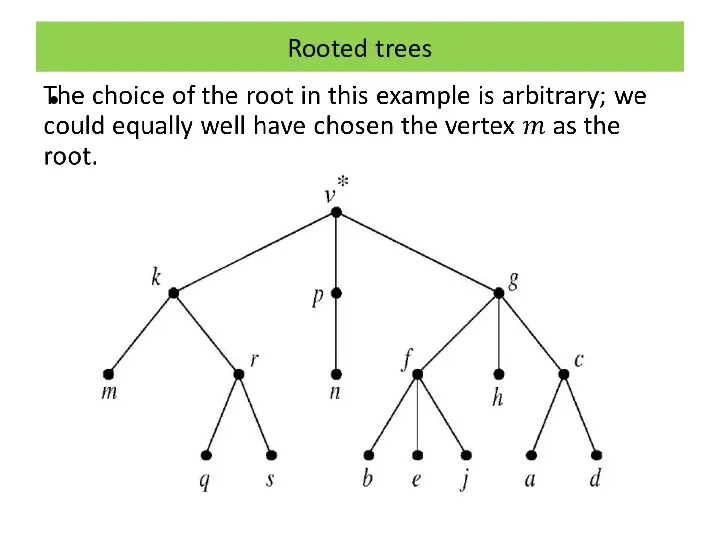
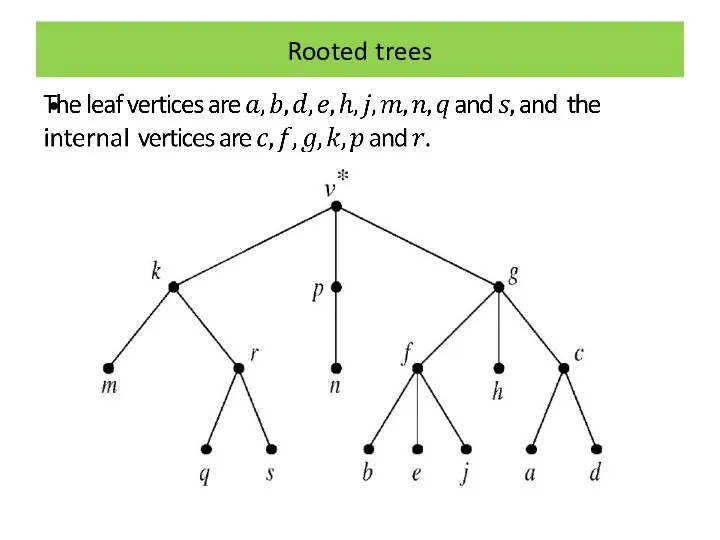
Rooted trees
Many of the applications of graph theory, particularly in computing,
use a certain kind of tree, called a ‘rooted tree’.
This is simply a tree where a particular vertex has been distinguished or singled out from the rest.
Слайд 47

Rooted trees
For example, family tree are graphs that represent genealogical charts.
Слайд 48
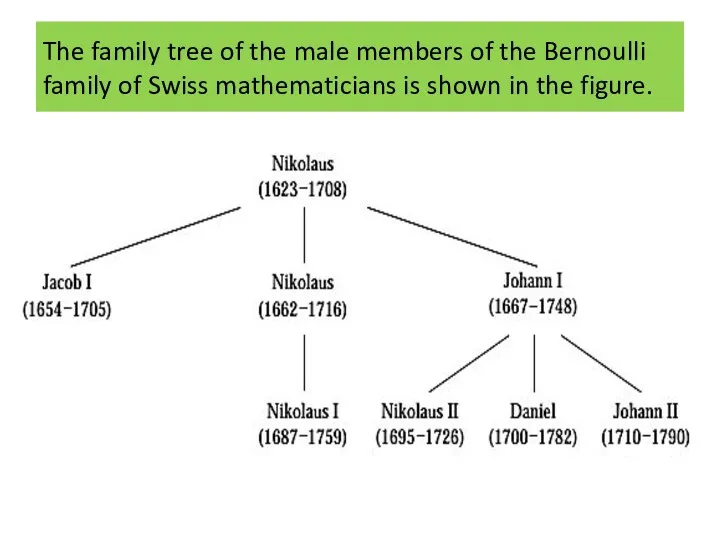
The family tree of the male members of the Bernoulli family
of Swiss mathematicians is shown in the figure.
Слайд 49

Rooted trees
Family trees use vertices to represent the members of a
family and edges to represent parent – child relationships.
The undirected graph representing a family tree (restricted to people of just one gender and with no inbreeding) is an example of a rooted tree.
Слайд 50
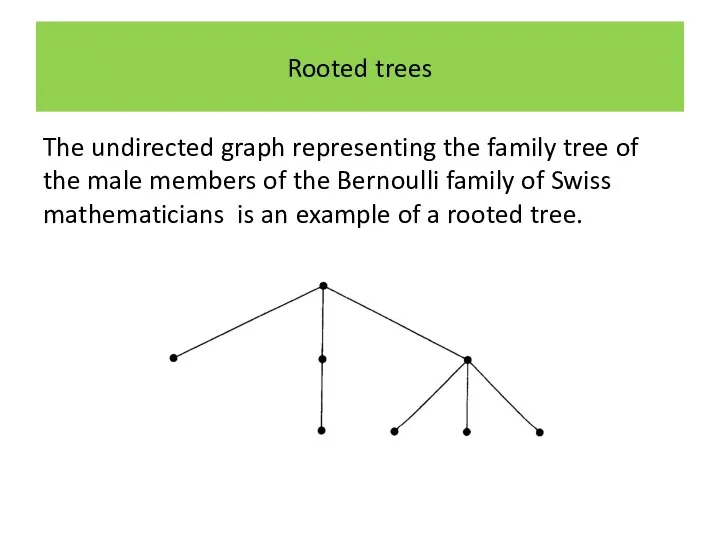
Rooted trees
The undirected graph representing the family tree of the male
members of the Bernoulli family of Swiss mathematicians is an example of a rooted tree.
Слайд 51
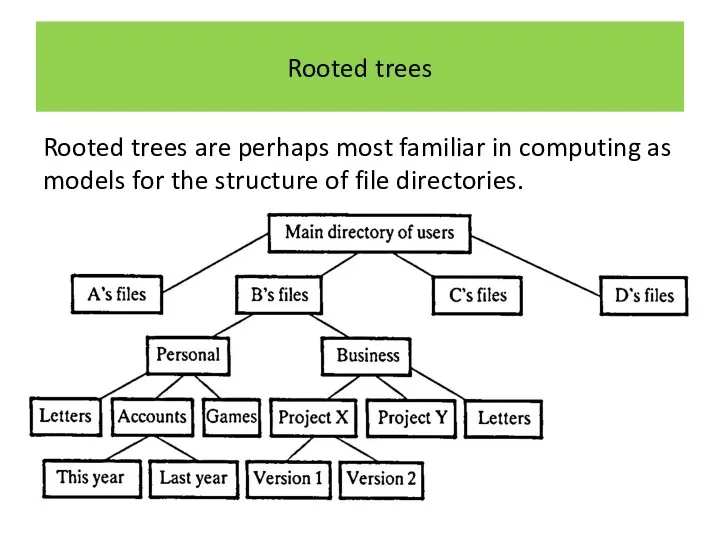
Rooted trees
Rooted trees are perhaps most familiar in computing as models
for the structure of file directories.
Слайд 52

Rooted trees
Some of the other important uses of rooted trees in
computing include the representation of data and the representation of algebraic expressions.
Слайд 53

Слайд 54
Слайд 55

Слайд 56
Слайд 57
Слайд 58
Слайд 59

Слайд 60
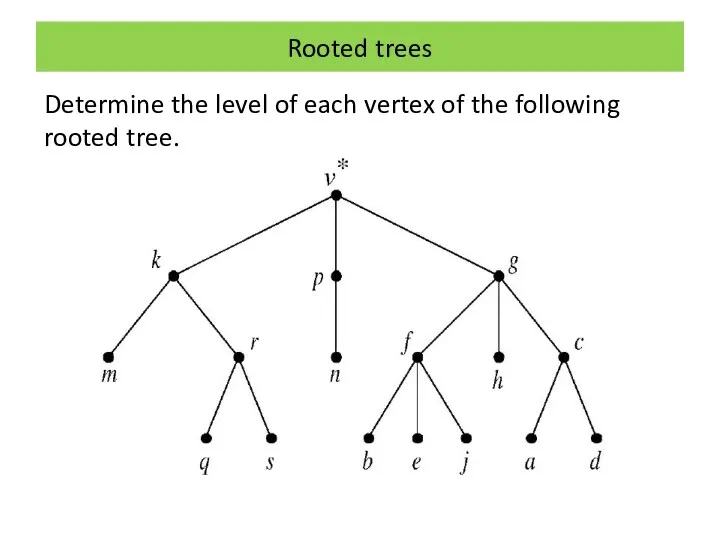
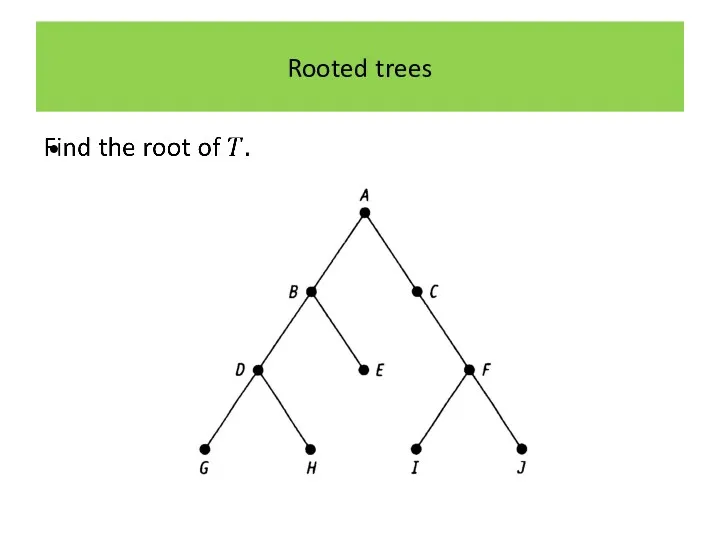
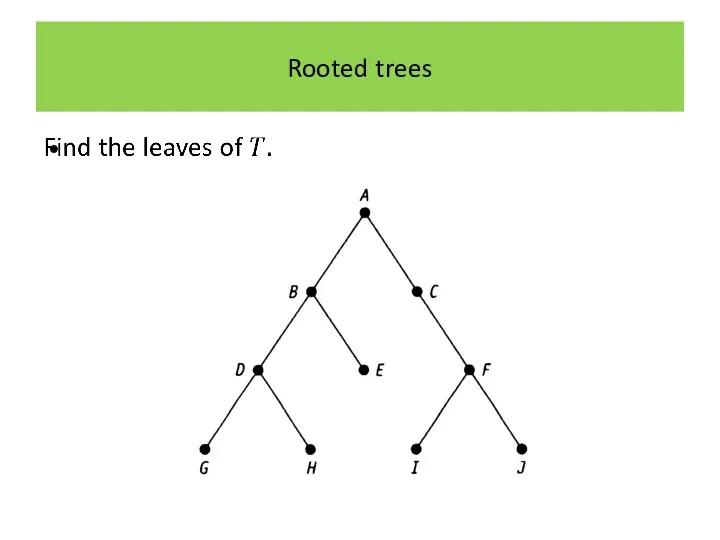
Rooted trees
Determine the level of each vertex of the following rooted
tree.
Слайд 61

Слайд 62

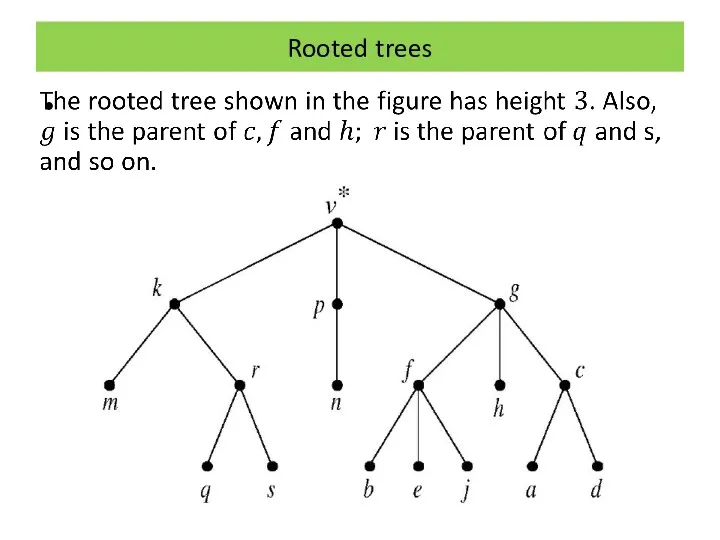
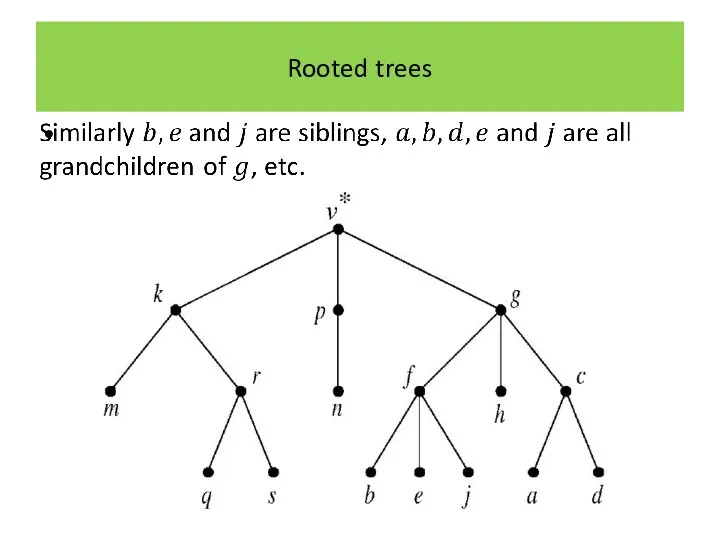
Rooted trees
It is clearly possible to define further terms such as
grandparent, grandchild, ancestor, descendant, etc.
Слайд 63
Слайд 64
Слайд 65

Rooted trees
Rooted trees can be used as models in such diverse
areas as
computer science,
biology,
management.
Слайд 66

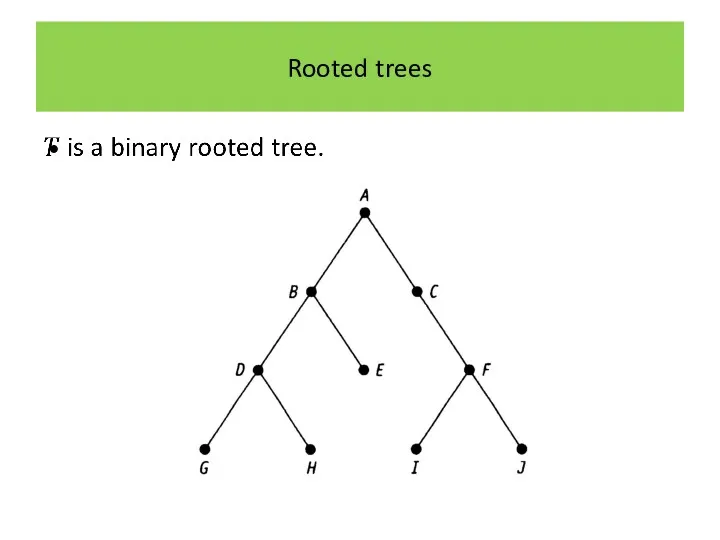
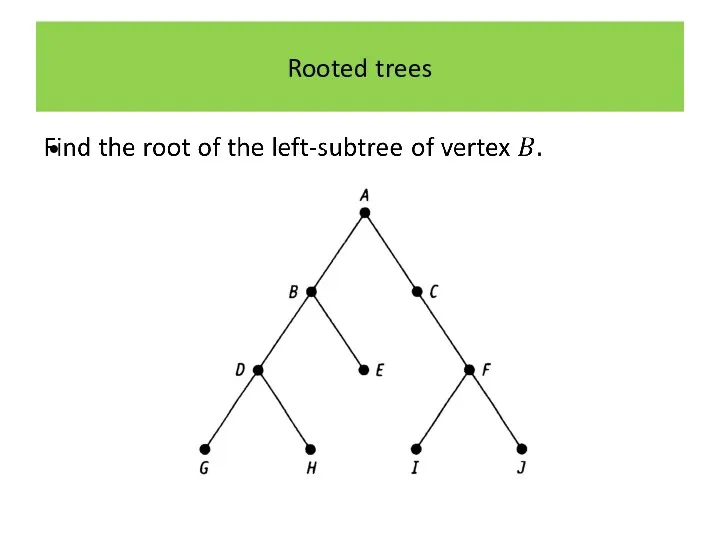
Rooted trees
Of particular importance in applications in computing are binary rooted
trees.
A binary rooted tree has a property that each vertex has at most two children.
In a binary rooted tree the two subtrees of a vertex are referred to as the left-subtree and the right-subtree of the vertex.
If a vertex has no left child its left-subtree is said to be the null tree (i.e. a tree with no vertices).
Similarly, if a vertex has no right child its right-subtree is said to be the null tree.
Слайд 67

Слайд 68

Слайд 69
Слайд 70
Слайд 71
Слайд 72







































































 Салыстыру және логикалық операторларды қолдану
Салыстыру және логикалық операторларды қолдану Параллельное программирование для ресурсоёмких задач численного моделирования в физике. Лекция 2
Параллельное программирование для ресурсоёмких задач численного моделирования в физике. Лекция 2 Анализ и мониторинг интернет-СМИ. Базы СМИ. Медиаисследования в интернете
Анализ и мониторинг интернет-СМИ. Базы СМИ. Медиаисследования в интернете CSS. Лекция 10
CSS. Лекция 10 Компьютерные словари и системы машинного перевода текстов
Компьютерные словари и системы машинного перевода текстов Інформаційні системи. Інтелектуальна власність та авторське право
Інформаційні системи. Інтелектуальна власність та авторське право Синхронизация в OpenMP
Синхронизация в OpenMP Counter-Strike: Global Offensive. Разработка компьютерных игр
Counter-Strike: Global Offensive. Разработка компьютерных игр Прийоми забезпечення технологічності програмних продуктів. Низхідне та висхідне програмування. Метод покрокової деталізації
Прийоми забезпечення технологічності програмних продуктів. Низхідне та висхідне програмування. Метод покрокової деталізації Z-передаточная функция и весовая последовательность цифрового блока. (Лекция 6)
Z-передаточная функция и весовая последовательность цифрового блока. (Лекция 6) Масиви. Введення даних у масив
Масиви. Введення даних у масив Қатты диск құрылысы. Жинақтауыштың негізгі түйіндері
Қатты диск құрылысы. Жинақтауыштың негізгі түйіндері Разработка модуля CMS Drupal для создания тестов и оценки знаний пользователей
Разработка модуля CMS Drupal для создания тестов и оценки знаний пользователей Засоби UML для моделювання в програмній інженерії
Засоби UML для моделювання в програмній інженерії Грошові перекази та інтернет- магазини
Грошові перекази та інтернет- магазини Интернет Вещей. Умный дом как пример технологии
Интернет Вещей. Умный дом как пример технологии Розвиток інформатики в Україні
Розвиток інформатики в Україні Сетевая журналистика
Сетевая журналистика Текстовый редактор Microsoft office Word
Текстовый редактор Microsoft office Word Welcome To Epson Printer Customer Care Center
Welcome To Epson Printer Customer Care Center Памятка для школьника. Как создать виртуальную экскурсию в программе Microsoft Office PowerPoint
Памятка для школьника. Как создать виртуальную экскурсию в программе Microsoft Office PowerPoint SAP HANA – платформа для бизнеса в реальном времени
SAP HANA – платформа для бизнеса в реальном времени Моделирование памяти. Информационные объекты MATRIX. Организация циклов
Моделирование памяти. Информационные объекты MATRIX. Организация циклов Вычисления в таблицах Excel
Вычисления в таблицах Excel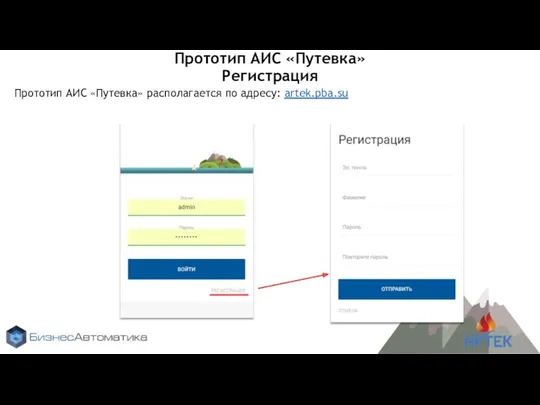 Прототип АИС Путевка. Регистрация
Прототип АИС Путевка. Регистрация Алгоритм построения орграфа Хаффмана (алгоритм сжатия)
Алгоритм построения орграфа Хаффмана (алгоритм сжатия) Поиск и сортировка информации в базах данных. ЕГЭ
Поиск и сортировка информации в базах данных. ЕГЭ Браузеры и поисковые системы
Браузеры и поисковые системы