Содержание
- 2. Методы защиты информации
- 3. Что такое криптология?
- 4. Криптография обеспечивает
- 5. Области применения криптографии
- 6. Периоды развития криптографии
- 7. Шифры и ключи Основное понятие в криптографии – шифр. Шифр – это преобразование исходного, секретного сообщения
- 8. Классы шифров Шифры простой замены шифр Цезаря, квадрат Полибия, шифр Плейфера, двойной квадрат. Шифры перестановки сциталь
- 9. Криптография базируется на следующих разделах математики: теория чисел линейная алгебра алгебраические структуры
- 10. Арифметика целых чисел использует множество целых чисел Z={ …, -3,-2,-1,0,1,2,3,…} бинарные операции: +, -, х
- 11. Деление целых чисел В арифметике целых чисел результатом деления а на n являются два числа q
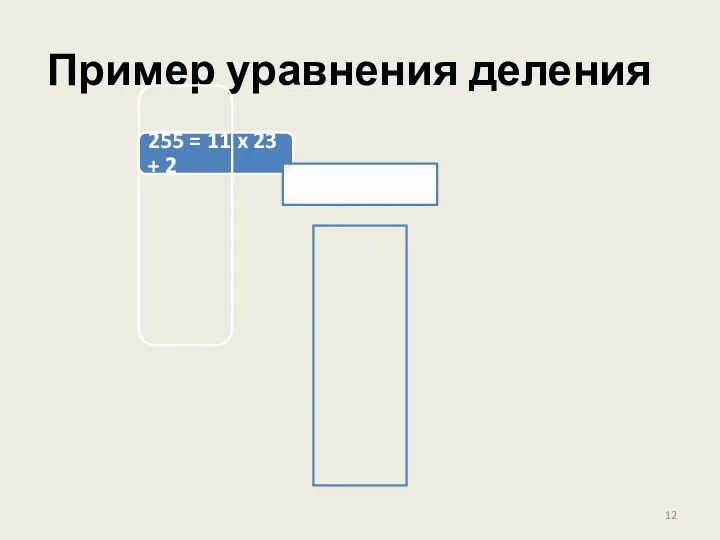
- 12. Пример уравнения деления 255 = 11 x 23 + 2
- 13. Ограничения на уравнения деления в криптографии Ограничение 1 делитель должен быть положительным целым числом ( n
- 14. Обозначение делимости Если в уравнении деления r = 0, то есть a = q x n,
- 15. Наибольший общий делитель Два положительных целых числа могут иметь много общих делителей, но только один наибольший
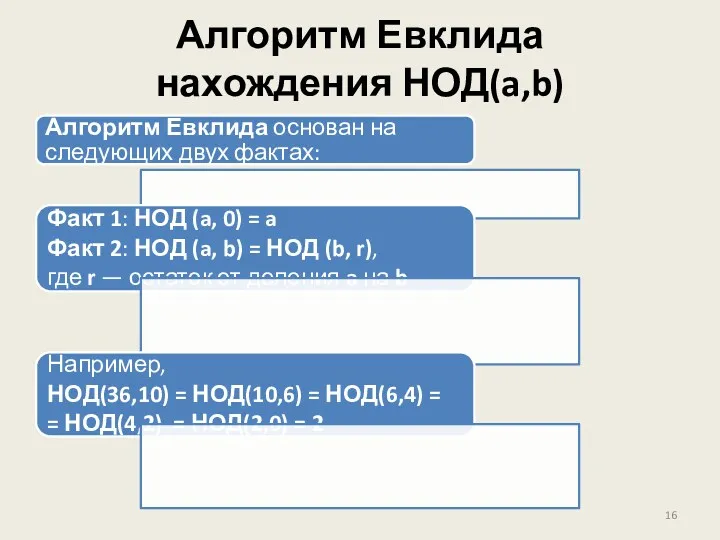
- 16. Алгоритм Евклида нахождения НОД(a,b) Алгоритм Евклида основан на следующих двух фактах: Факт 1: НОД (a, 0)
- 17. Алгоритм Евклида на языке псевдокода
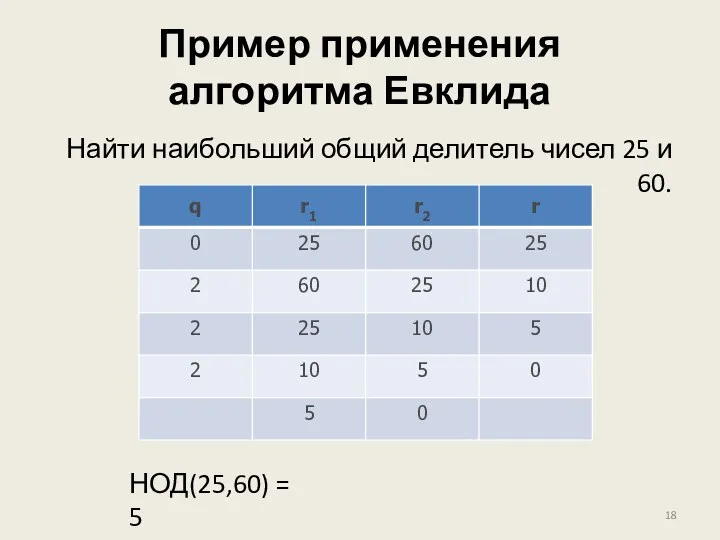
- 18. Пример применения алгоритма Евклида Найти наибольший общий делитель чисел 25 и 60. НОД(25,60) = 5
- 19. Расширенный алгоритм Евклида Позволяет найти для целых чисел a и b такие два целых числа s
- 20. Расширенный алгоритм Евклида на языке псевдокода
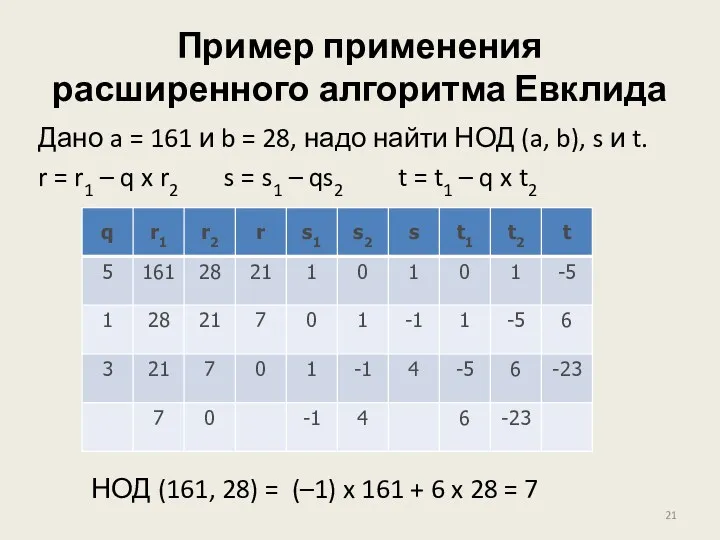
- 21. Пример применения расширенного алгоритма Евклида Дано a = 161 и b = 28, надо найти НОД
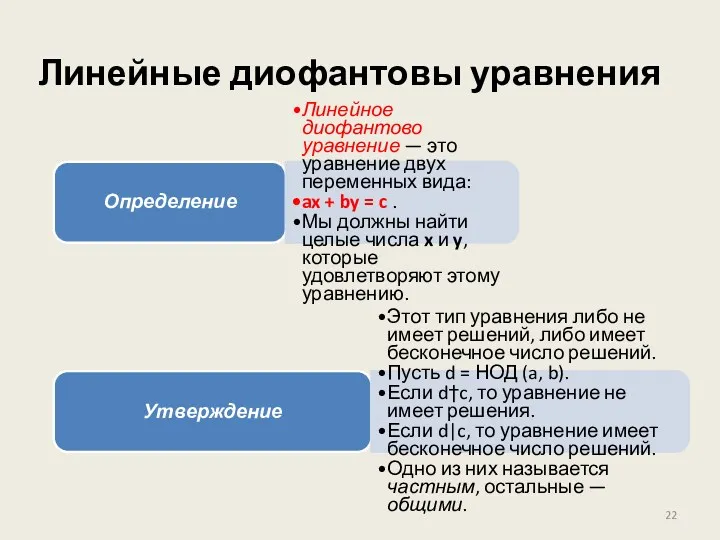
- 22. Линейные диофантовы уравнения Определение Линейное диофантово уравнение — это уравнение двух переменных вида: ax + by
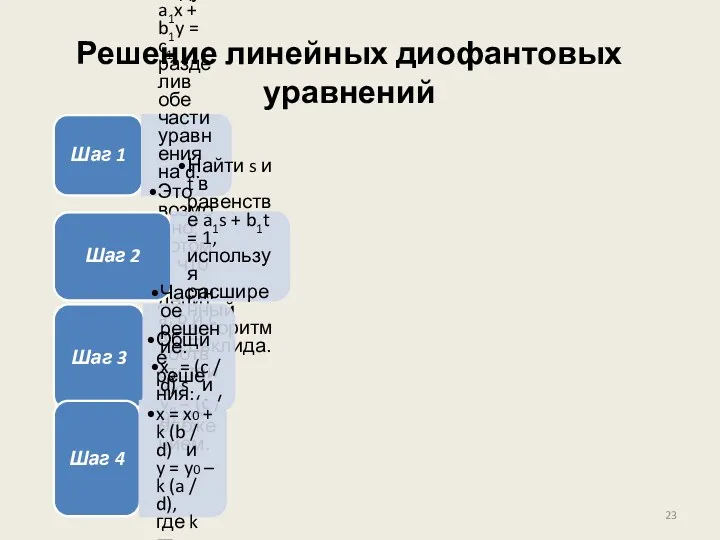
- 23. Решение линейных диофантовых уравнений Шаг 1 Если d|c, преобразуем уравнение к виду a1x + b1y =
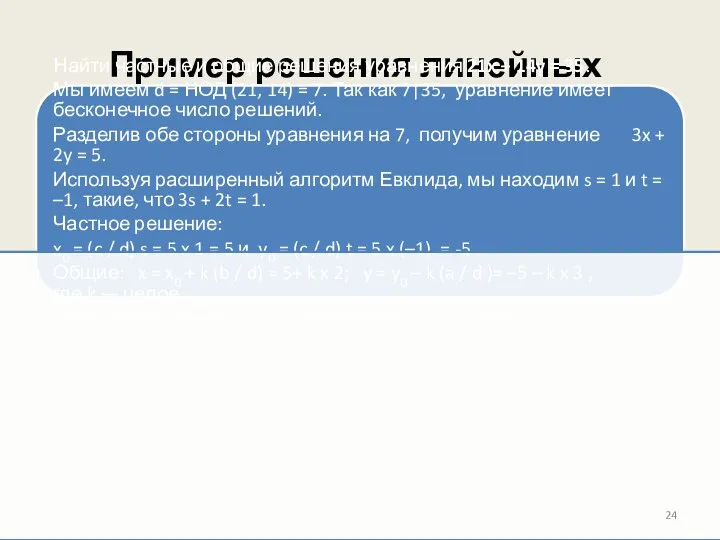
- 24. Пример решения линейных диофантовых уравнений Найти частные и общие решения уравнения 21x + 14y = 35.
- 25. Пример приложения диофантовых уравнений Мы хотим обменять денежный чек 100$ на некоторое число банкнот 20$ и
- 26. Операции по модулю Пусть a = q x n + r. Тогда говорят, что a равно
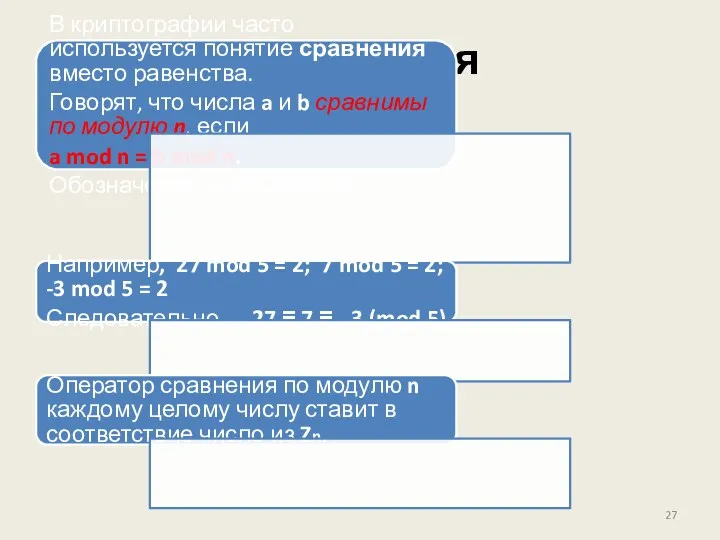
- 27. Сравнения В криптографии часто используется понятие сравнения вместо равенства. Говорят, что числа a и b сравнимы
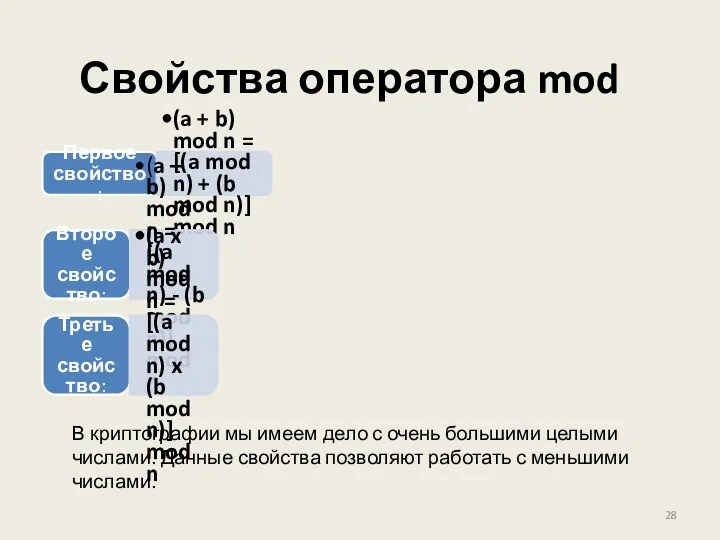
- 28. Свойства оператора mod Первое свойство: (a + b) mod n = [(a mod n) + (b
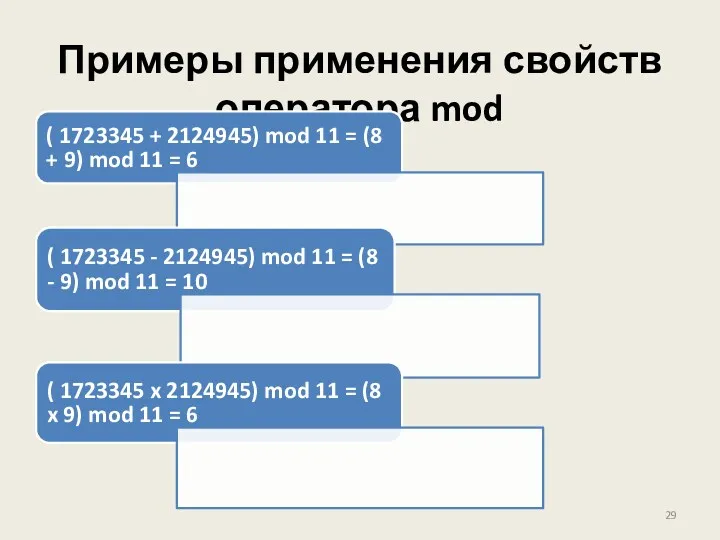
- 29. Примеры применения свойств оператора mod ( 1723345 + 2124945) mod 11 = (8 + 9) mod
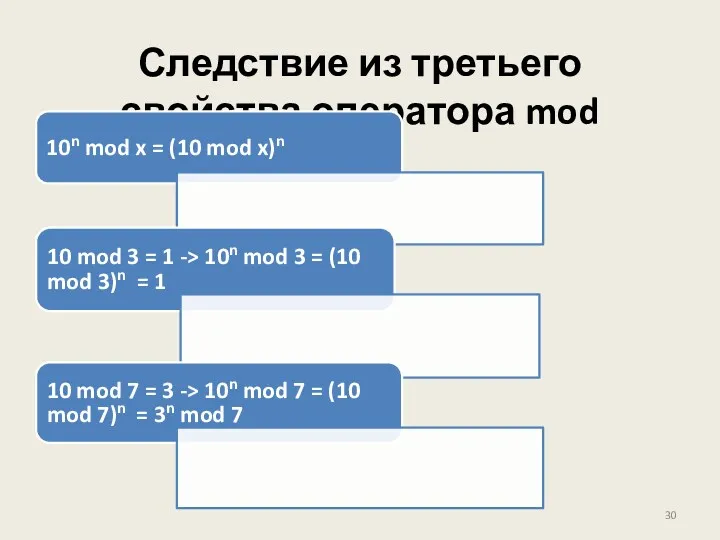
- 30. Следствие из третьего свойства оператора mod 10n mod x = (10 mod x)n 10 mod 3
- 31. Применение свойств оператора mod В арифметике остаток от целого числа, разделенного на 3, такой же, как
- 32. Аддитивная инверсия Определение Говорят, что в Zn два числа a и b аддитивно инверсны друг другу,
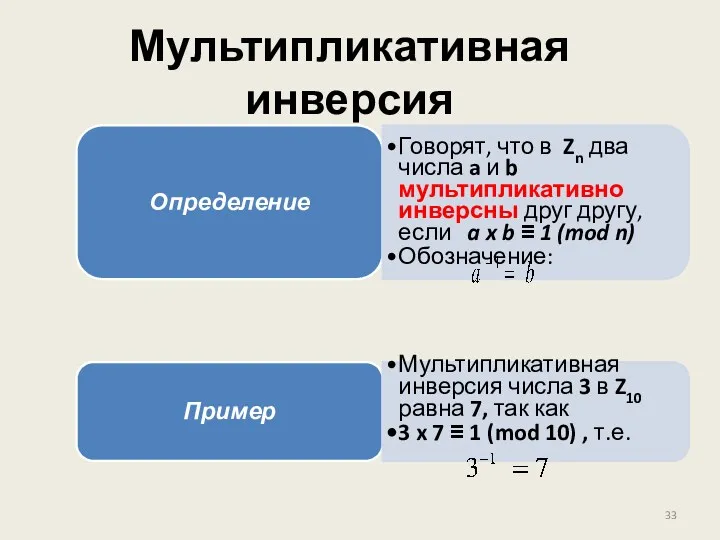
- 33. Мультипликативная инверсия Определение Говорят, что в Zn два числа a и b мультипликативно инверсны друг другу,
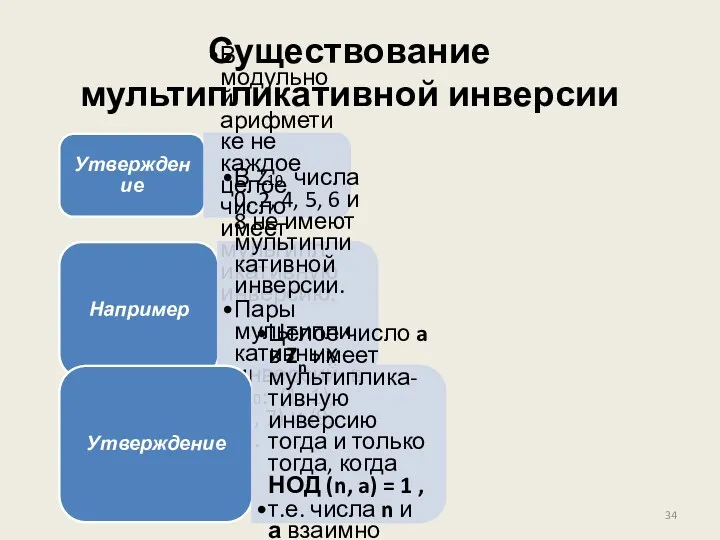
- 34. Существование мультипликативной инверсии Утверждение В модульной арифметике не каждое целое число имеет мультипликативную инверсию. Например В
- 35. Таблицы сложения и умножения в Z10
- 36. Различные множества для сложения и умножения В криптографии мы часто работаем с инверсиями. Если отправитель посылает
- 37. Множества Zn и Zn* Утверждение Каждый член Zn имеет аддитивную инверсию, но только некоторые члены имеют
- 38. Примеры множеств Zn и Zn*
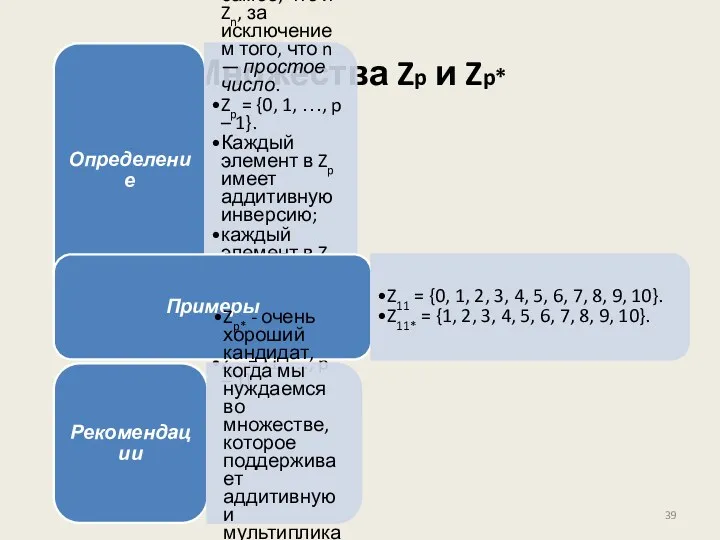
- 39. Множества Zp и Zp* Определение Множество Zp — то же самое, что и Zn, за исключением
- 40. Нахождение мультипликативной инверсии Расширенный алгоритм Евклида может найти мультипликативную инверсию b в Zn, когда инверсия существует,
- 41. Расширенный алгоритм Евклида для нахождения мультипликативной инверсии
- 42. Пример нахождения мультипликативной инверсии Найти мультипликативную инверсию числа 11 в Z26. НОД (11, 26) = 1
- 43. Линейные уравнения с одним неизвестным, содержащие сравнения
- 44. Решение линейных сравнений с одним неизвестным
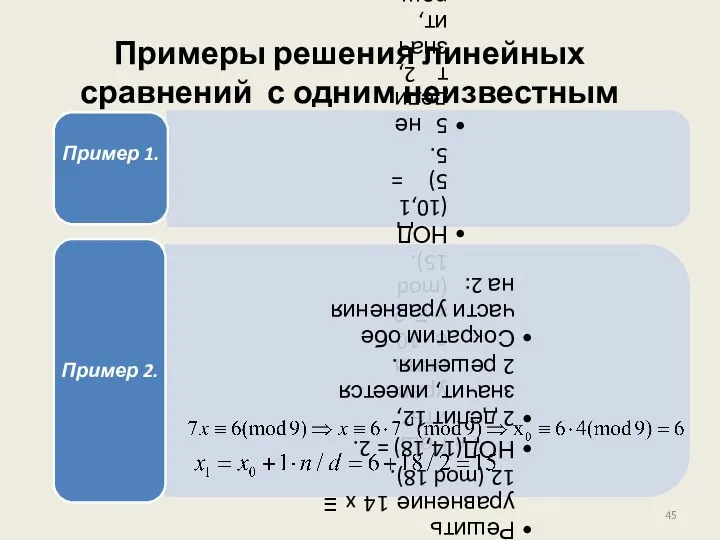
- 45. Примеры решения линейных сравнений с одним неизвестным
- 46. Матрицы вычетов
- 47. Сравнение матриц
- 48. Операции над матрицами вычетов
- 49. Примеры операций над матрицами вычетов A - матрица вычетов в Z26 . det (A) = 21
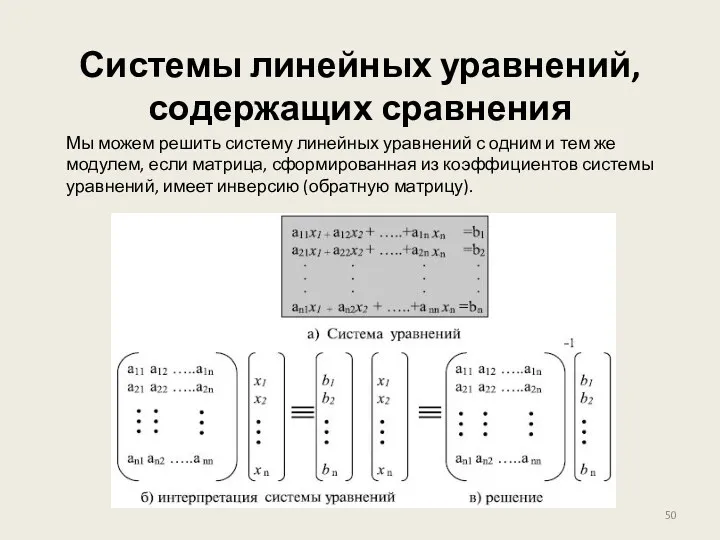
- 50. Системы линейных уравнений, содержащих сравнения Мы можем решить систему линейных уравнений с одним и тем же
- 51. Обзорные вопросы по лекции 1 Покажите различие между Z и Zn. Какое из этих множеств может
- 53. Скачать презентацию

































 Flight controls
Flight controls Искусственный интеллект
Искусственный интеллект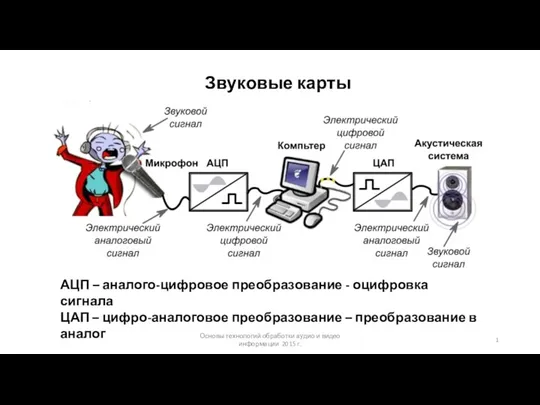 Звуковые карты
Звуковые карты Трёхмерная графика и 3D - моделирование
Трёхмерная графика и 3D - моделирование Методы исследования инфокоммуникаций
Методы исследования инфокоммуникаций Промышленные сети
Промышленные сети Теория автоматов и формальных языков. Абстрактный синтез
Теория автоматов и формальных языков. Абстрактный синтез Принципы управления, построения и алгоритмы функционирования элементов САУ и СА
Принципы управления, построения и алгоритмы функционирования элементов САУ и СА Безопасность в Интернете
Безопасность в Интернете Мультимедийная разработка учебного занятия
Мультимедийная разработка учебного занятия Животные и их дети
Животные и их дети BlaBlaCar. Communication Plan
BlaBlaCar. Communication Plan Операционные системы. Основные характеристики операционных систем. Внеаудиторная работа №6
Операционные системы. Основные характеристики операционных систем. Внеаудиторная работа №6 Двоичное кодирование
Двоичное кодирование Introducing the C# Class Types. Defining classes, objects and methods
Introducing the C# Class Types. Defining classes, objects and methods Операционные системы
Операционные системы Системы счисления
Системы счисления Ограничение и сортировка данных
Ограничение и сортировка данных Обзор компьютерной игры “Valorant”
Обзор компьютерной игры “Valorant” Электронный сервис Публичная кадастровая карта
Электронный сервис Публичная кадастровая карта Условный оператор 1
Условный оператор 1 Тема 4: Призначення, особливості та можливості СУБД Ms Access
Тема 4: Призначення, особливості та можливості СУБД Ms Access Тест по теме:Условный оператор Диск
Тест по теме:Условный оператор Диск Создание 3d-модели современного кабинета информатики
Создание 3d-модели современного кабинета информатики Функциональное и доменное тестирование
Функциональное и доменное тестирование Мобильное приложение: онлайн-магазин одежды
Мобильное приложение: онлайн-магазин одежды Подготовка к ОГЭ по информатике
Подготовка к ОГЭ по информатике Как работают чат-боты и кто их разрабатывает?
Как работают чат-боты и кто их разрабатывает?