Содержание
- 2. Решение: Поскольку один символ кодируется двумя байтами, из текста удалили 8 символов. Заметим, что лишние запятая
- 3. ОГЭ_ 2 Даны три кодовые цепочки: 10111101 1010110 10111000 Найдите среди них ту, которая имеет только
- 4. Решение: Проанализируем каждый вариант ответа: 1) «10111101» может означать как «КОА», так и «НОК». 2) «1010110»
- 5. ОГЭ_3 Напишите наименьшее целое число x, для которого истинно высказывание: НЕ (X
- 6. Решение: Логическое «И» ложно тогда, когда ложно одно из высказываний. Запишем выражение в виде (X >=
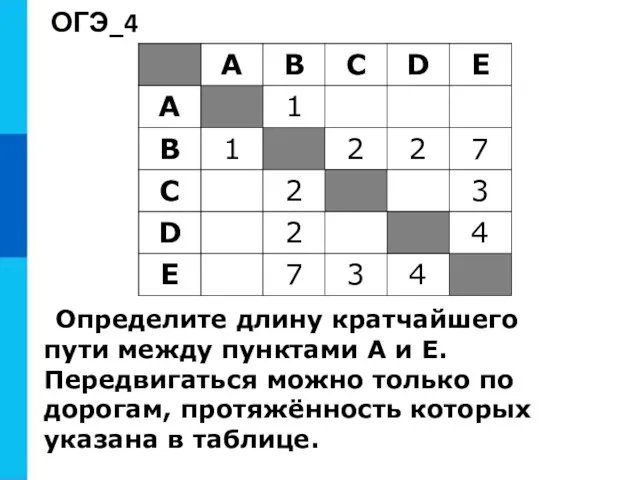
- 7. ОГЭ_4 Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость
- 8. Решение: Найдём все варианты маршрутов из A в E и выберем самый короткий. A—B: длина маршрута
- 9. ОГЭ_5 У исполнителя Альфа две команды, которым присвоены номера: 1. прибавь 1; 2. умножь на b
- 10. ОГЭ _7 Доступ к файлу slon.txt, находящемуся на сервере circ.org, осуществляется по протоколу http. Фрагменты адреса
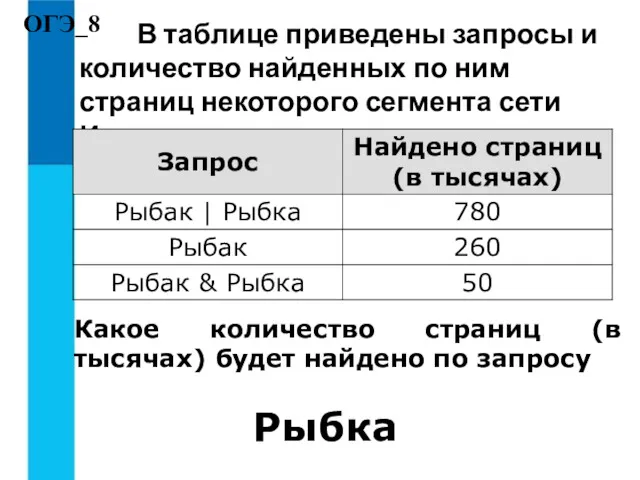
- 11. ОГЭ_8 В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. Какое
- 12. Решение: Представим таблицу в виде кругов Эйлера. Пусть Рыбак — круг 1, Рыбка — круг 3.
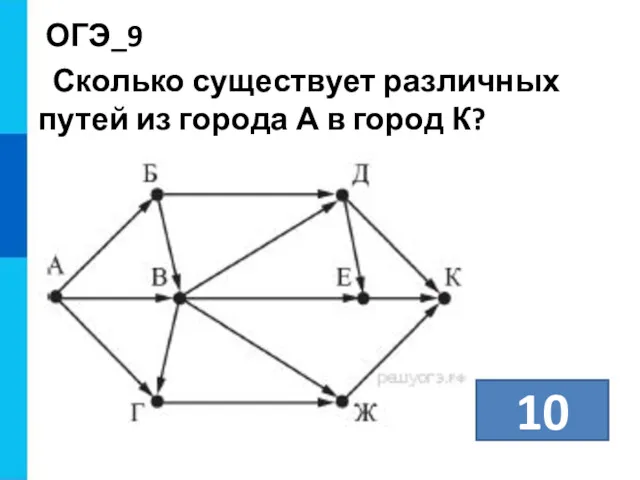
- 13. ОГЭ_9 Сколько существует различных путей из города А в город К? 10
- 14. ОГЭ_10 Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его
- 16. Скачать презентацию










 Базы данных
Базы данных Операции, линейный алгоритм. (Семинар 1-3)
Операции, линейный алгоритм. (Семинар 1-3) Инстаграм от 0 до 100 000
Инстаграм от 0 до 100 000 Информатика. Введение
Информатика. Введение Прикладной уровень стека TCP/IP
Прикладной уровень стека TCP/IP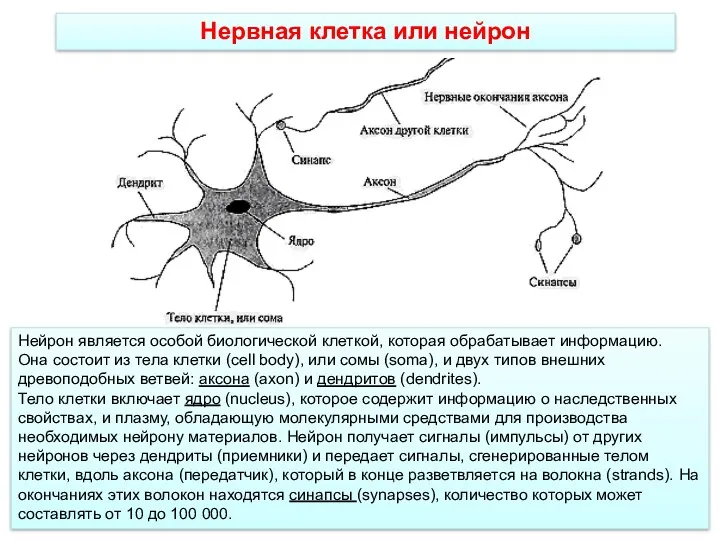 Нейронные сети
Нейронные сети Самая крупная партнерская сеть в нише онлайн-обучения
Самая крупная партнерская сеть в нише онлайн-обучения Использование сети Интернет террористическими и экстремистскими организациями
Использование сети Интернет террористическими и экстремистскими организациями Computer Science 686 Spring 2007. Intel EM64T and VT Extensions
Computer Science 686 Spring 2007. Intel EM64T and VT Extensions Установка операционной системы на ПК, серверах, а также правила настройки интерфейса пользователя
Установка операционной системы на ПК, серверах, а также правила настройки интерфейса пользователя Глобальная сеть
Глобальная сеть WORD.Работа с таблицей (меню и панель инструментов).
WORD.Работа с таблицей (меню и панель инструментов). Кодирование графической информации
Кодирование графической информации Методический материал по теме Лабораторные и практические работы как средство эффективной реализации аудиторной самостоятельной работы студентов
Методический материал по теме Лабораторные и практические работы как средство эффективной реализации аудиторной самостоятельной работы студентов ВКонтакте
ВКонтакте Объектные привилегии
Объектные привилегии Навигатор дополнительного образования детей Ульяновской области
Навигатор дополнительного образования детей Ульяновской области Первинний статистичний аналіз програмного забеспечення. (Лекція 10)
Первинний статистичний аналіз програмного забеспечення. (Лекція 10) Protecting the Network
Protecting the Network Подпрограммы
Подпрограммы Digital Twin. Занятие 2
Digital Twin. Занятие 2 Компьютерный дизайн
Компьютерный дизайн Архитектура ЭВМ. Операционные системы. Потоки исполнения - Thread
Архитектура ЭВМ. Операционные системы. Потоки исполнения - Thread Компьютерлік графика негіздері Және оның түрлері
Компьютерлік графика негіздері Және оның түрлері Эффективный госпаблик школы
Эффективный госпаблик школы Базовая модель угроз безопасности персональных данных при их обработке в информационных системах персональных данных
Базовая модель угроз безопасности персональных данных при их обработке в информационных системах персональных данных Добро пожаловать в Компьютерную Академию TOP
Добро пожаловать в Компьютерную Академию TOP Spring data. Familiar and consistent programming model for data access
Spring data. Familiar and consistent programming model for data access