Содержание
- 2. Что такое вычислительная математика? Вычислительная математика — часть информатики, использующая математические методы. Часто этот термин трактуют
- 3. Что такое вычислительная математика? В свою очередь, прикладная математика включает в себя теорию численных методов и
- 5. Методы решения математических задач На отрезке [-10, 10]. Найти целые корни уравнения
- 6. Аналитическое решение
- 7. Численное решение Находим целые корни уравнения на отрезке простым перебором всех целых чисел на данном отрезке
- 9. Методы решения математических задач Аналитические Численные Достоинства — решения точные Недостатки — не всегда можно получить
- 10. Основные задачи поиск корней уравнения, поиск значения производной в заданной точке, вычисление определенного интеграла, вычисление значений
- 11. Решение уравнений
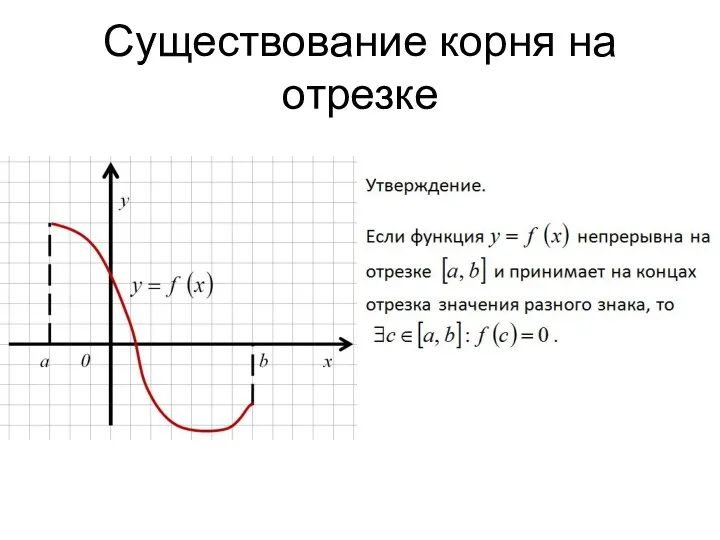
- 12. Существование корня на отрезке
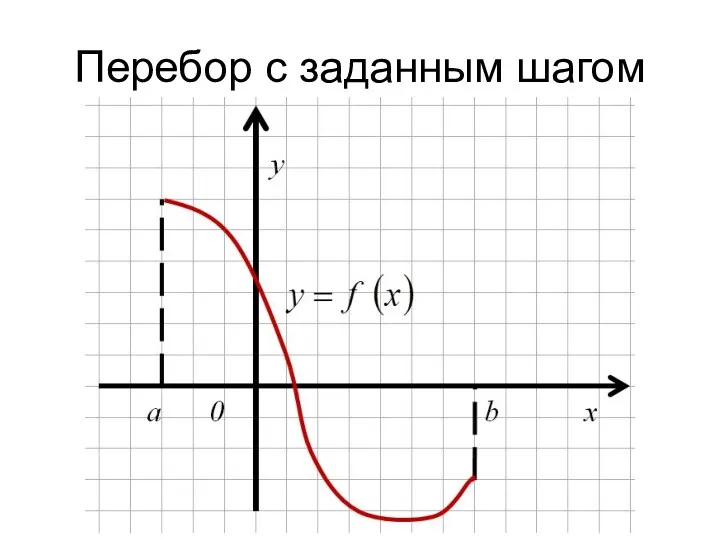
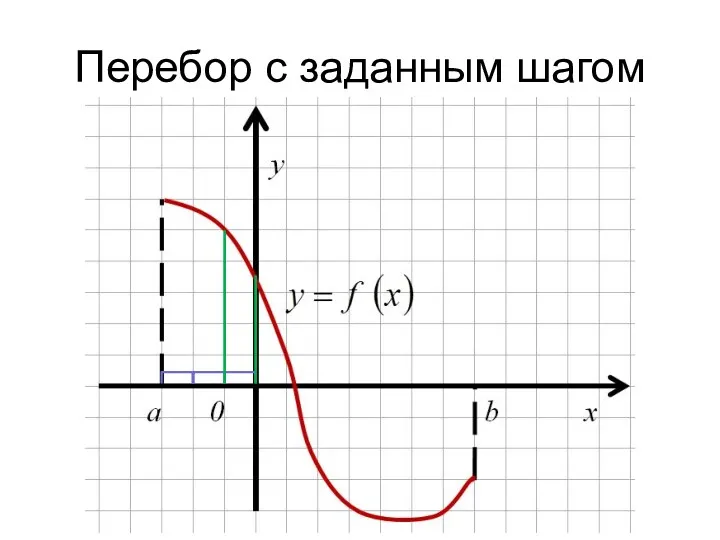
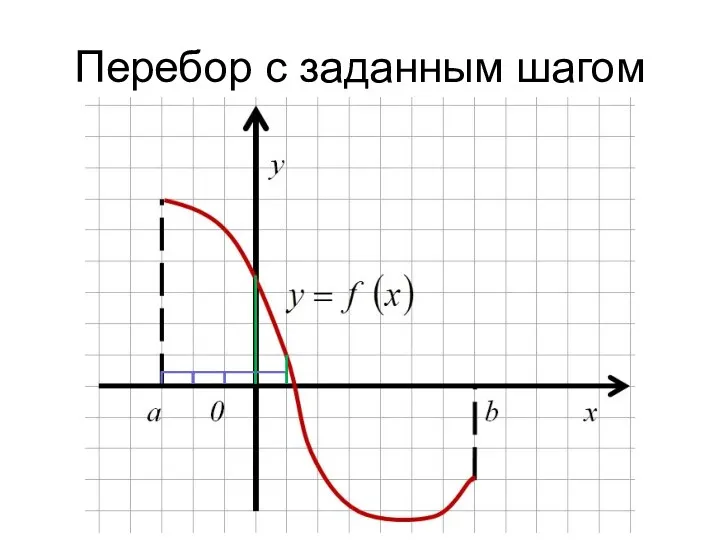
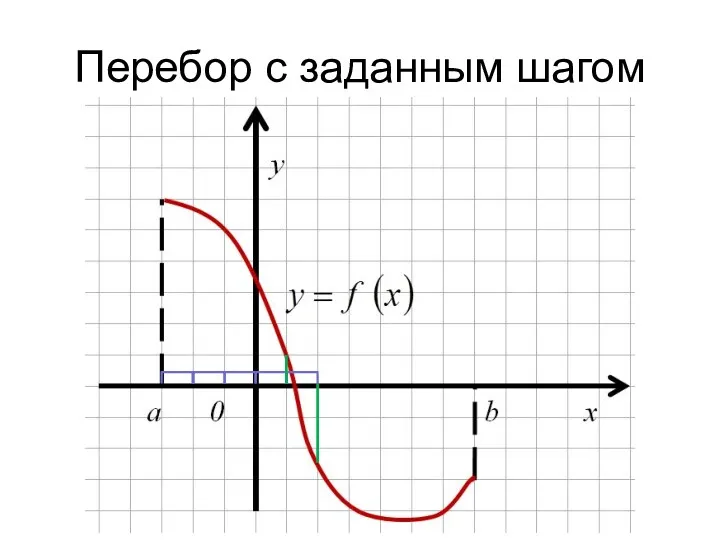
- 13. Перебор с заданным шагом
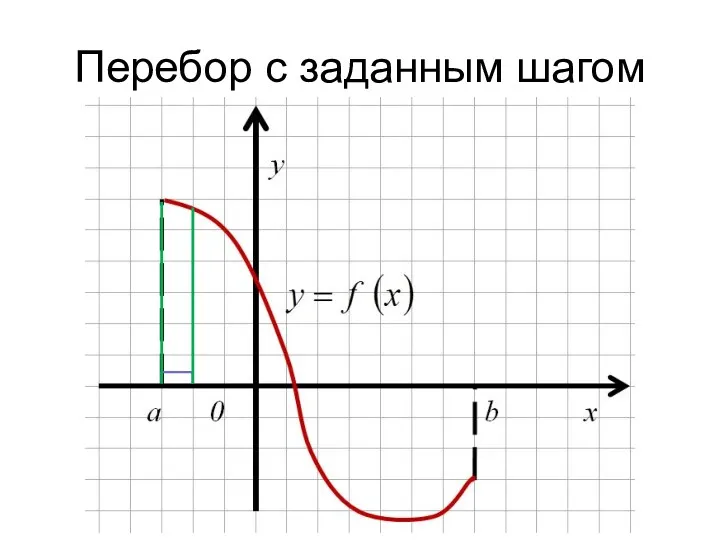
- 14. Перебор с заданным шагом
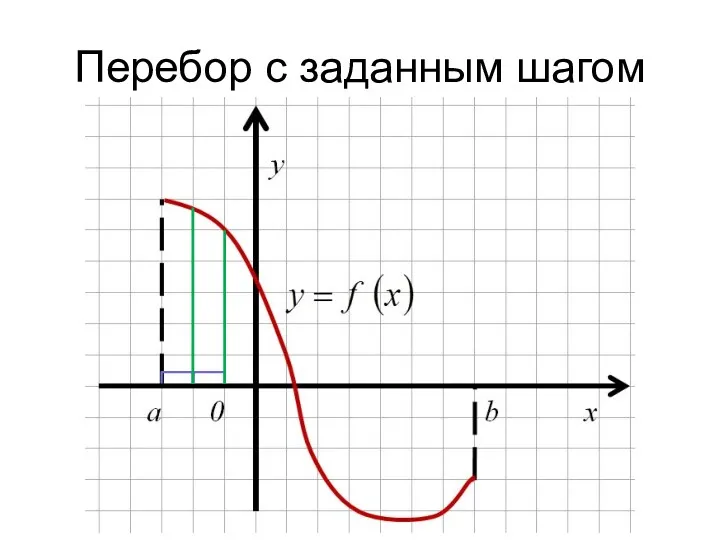
- 15. Перебор с заданным шагом
- 16. Перебор с заданным шагом
- 17. Перебор с заданным шагом
- 18. Перебор с заданным шагом
- 19. Уточнение корня на отрезке перебором с заданным шагом Покрываем отрезок [a, b] отрезками длиной ε ([a,
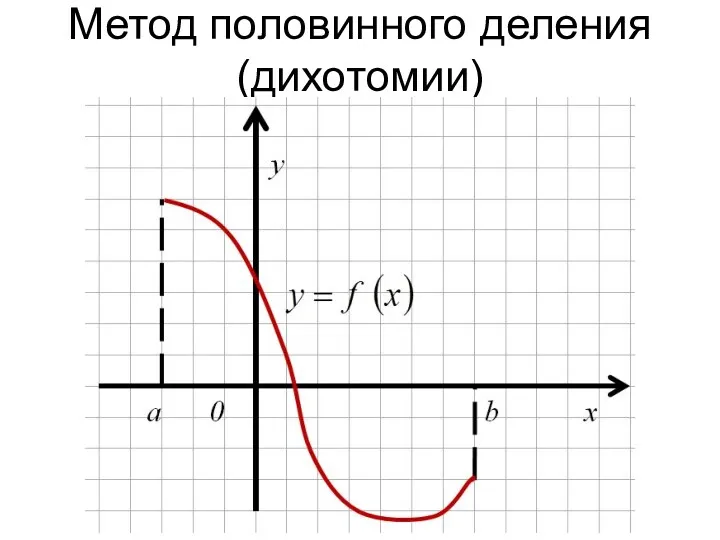
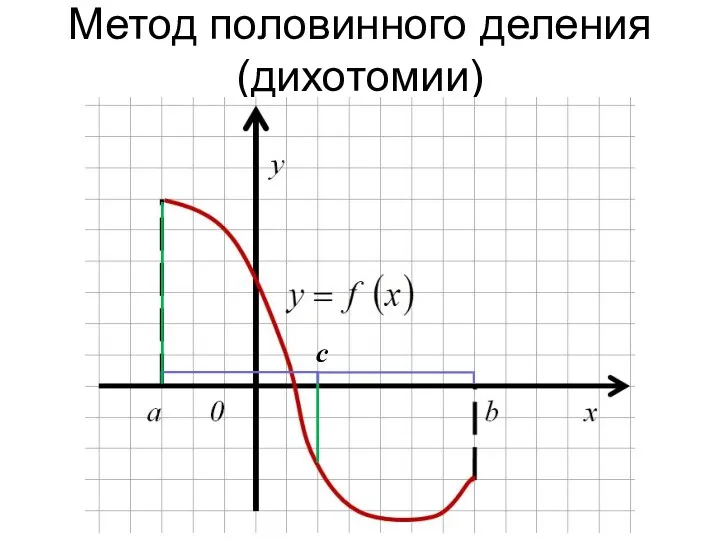
- 20. Метод половинного деления (дихотомии)
- 21. Метод половинного деления (дихотомии) c
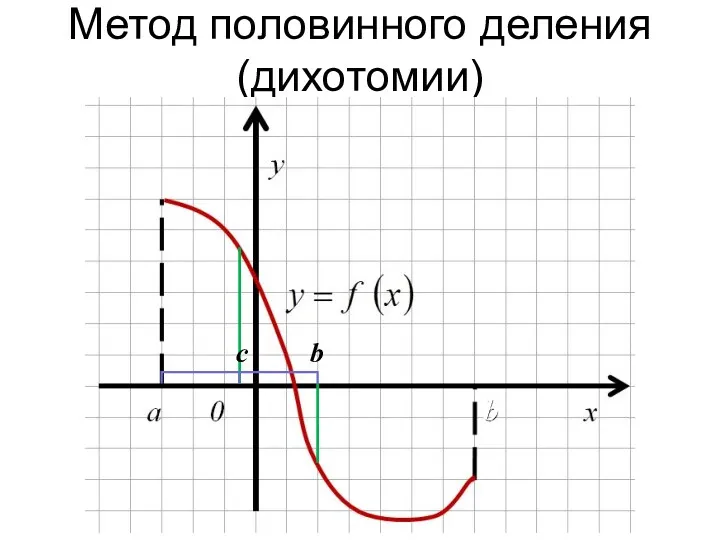
- 22. Метод половинного деления (дихотомии) c b b
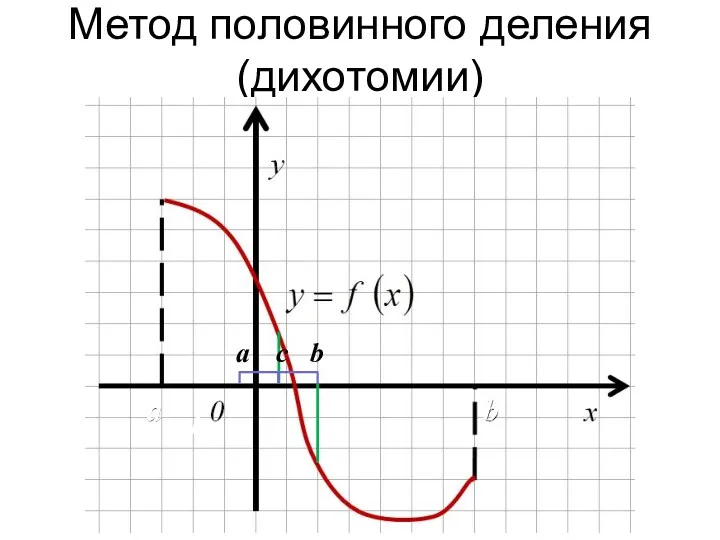
- 23. Метод половинного деления (дихотомии) a b b b a c
- 24. Уточнение корня на отрезке методом дихотомии Пока длина отрезка [a, b] больше ε, делим отрезок пополам
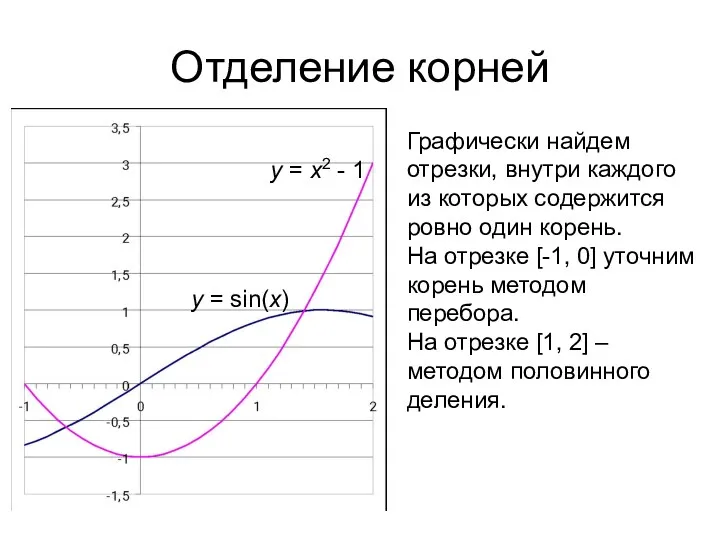
- 26. Отделение корней y = x2 - 1 y = sin(x) Графически найдем отрезки, внутри каждого из
- 27. Метод перебора program ex; uses crt; function f(x:real):real; begin f:=sqr(x)-1-sin(x) end; var y,x,a,b,c,eps,dx:real; n:integer; begin clrscr;
- 28. Метод перебора
- 29. Метод дихотомии program ex; uses crt; function f(x:real):real; begin f:=sqr(x)-1-sin(x) end; var y,x,a,b,c,eps,dx:real; n:integer; begin clrscr;
- 30. Метод дихотомии
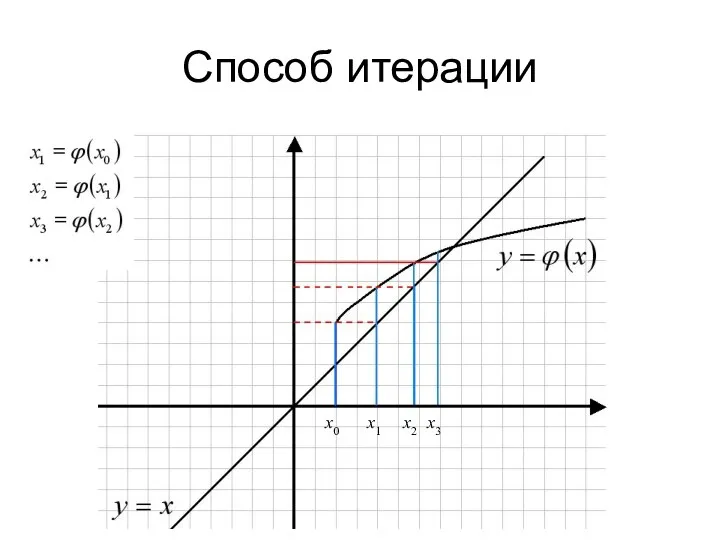
- 31. Способ итерации
- 32. Способ итерации Для применения способа итерации, получившего свое название от латинского слова iteratio – повторение, требуется
- 33. Способ итерации х0 х1 х2 х3
- 34. Условие применимости Теорема Если в некотором интервале, содержащем корень уравнения (*), следовательно и уравнения (**), выполняется
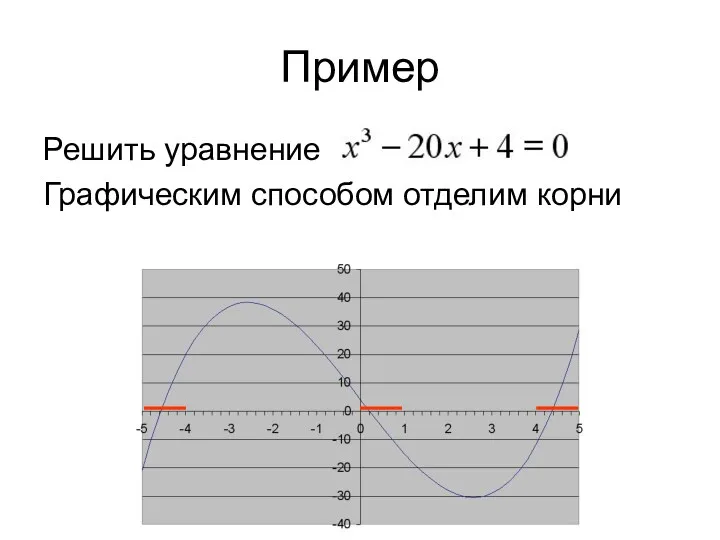
- 35. Пример Решить уравнение Графическим способом отделим корни
- 36. Пример Решить уравнение Преобразовать к виду (**) можно разными способами
- 37. Пример Второй способ непригоден ни на одном из интервалов, так как не удовлетворяет условию теоремы. Первый
- 38. Пример На интервалах (-5, -4) и (4, 5) первый способ не применим, зато примерим третий!
- 39. Пример Третий способ пригоден на интервалах (-5, -4) и (4, 5), так как удовлетворяет условию теоремы
- 41. Скачать презентацию



![Методы решения математических задач На отрезке [-10, 10]. Найти целые корни уравнения](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/371134/slide-4.jpg)




















 Квадратные уравнения
Квадратные уравнения Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Бифуркации и структурная устойчивость
Бифуркации и структурная устойчивость Классификация систем нечеткой логики
Классификация систем нечеткой логики Взаимно простые числа. Признак делимости на пр-е. НОК
Взаимно простые числа. Признак делимости на пр-е. НОК Транспортная задача. (Лекции 10,11)
Транспортная задача. (Лекции 10,11) Степенные ряды
Степенные ряды Геометрия Евклида
Геометрия Евклида Повторение. Решение задач и примеров
Повторение. Решение задач и примеров Многочлен и его стандартный вид
Многочлен и его стандартный вид Применение производной для нахождения наибольших и наименьших значений величин
Применение производной для нахождения наибольших и наименьших значений величин Платоновы тела
Платоновы тела Случаи вычитания 17 - 18 -
Случаи вычитания 17 - 18 - Математика. Задачи на космическую тему
Математика. Задачи на космическую тему Элементы теории вероятности и математической статистики
Элементы теории вероятности и математической статистики C_26
C_26 Математические основы доказательной медицины
Математические основы доказательной медицины Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. (Семинар 36)
Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. (Семинар 36) Внеклассное Математическое ассорти. 6 класс
Внеклассное Математическое ассорти. 6 класс Властивості коренів. Розв′язування задач
Властивості коренів. Розв′язування задач Доказательство теоремы
Доказательство теоремы Правильная четырехугольная пирамида. Задачи
Правильная четырехугольная пирамида. Задачи Презентации по математике
Презентации по математике Урок математики во втором классе
Урок математики во втором классе Графический метод решения системы двух линейных уравнений с двумя переменными. 7 класс
Графический метод решения системы двух линейных уравнений с двумя переменными. 7 класс Степенная функция и её свойства
Степенная функция и её свойства Задачи на повторение по геометрии. Подготовка к ГИА
Задачи на повторение по геометрии. Подготовка к ГИА Стандартный вид числа
Стандартный вид числа