Анализ временных рядов презентация

Лекция
Анализ временных рядов

Анализ временных рядов
временным рядом называют последовательность наблюдений, упорядоченных по времени
Аргумент (t) дискретно меняется через равные
промежутки.

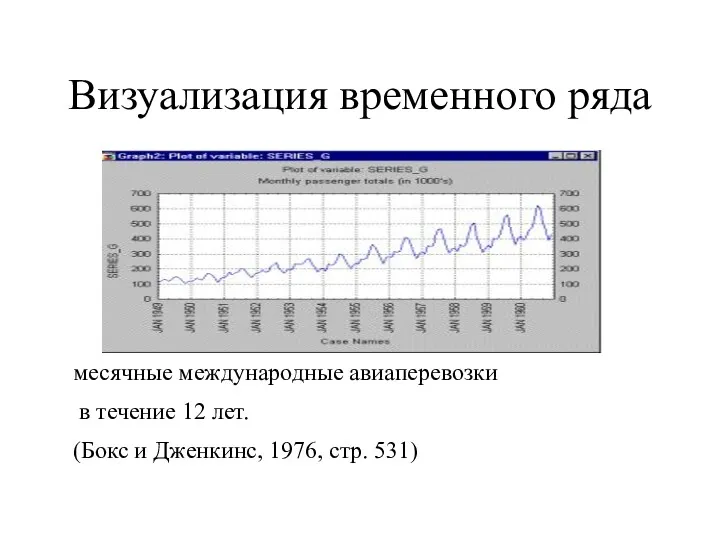
Визуализация временного ряда
месячные международные авиаперевозки
в течение 12 лет.
(Бокс и Дженкинс, 1976, стр. 531)

Модели временных рядов.
Такие модели объясняют поведение переменной, меняющейся с течением времени, исходя только из ее предыдущих значений. К этому классу относятся модели тренда, сезонности, тренда и сезонности (аддитивная и мультипликативная формы) и др.

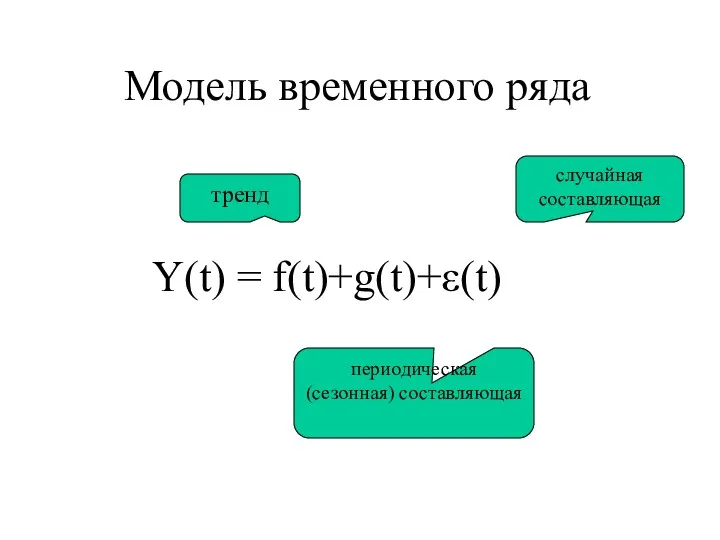
Модель временного ряда
Y(t) = f(t)+g(t)+ε(t)
случайная составляющая
периодическая (сезонная) составляющая
тренд

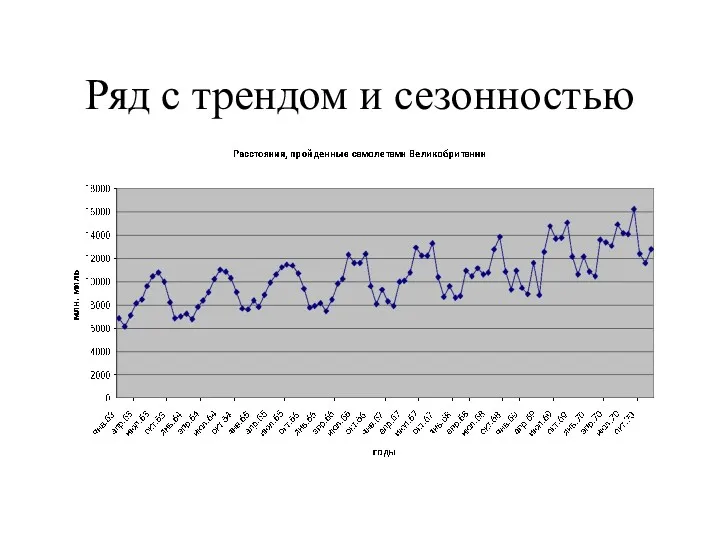
Ряд с трендом и сезонностью

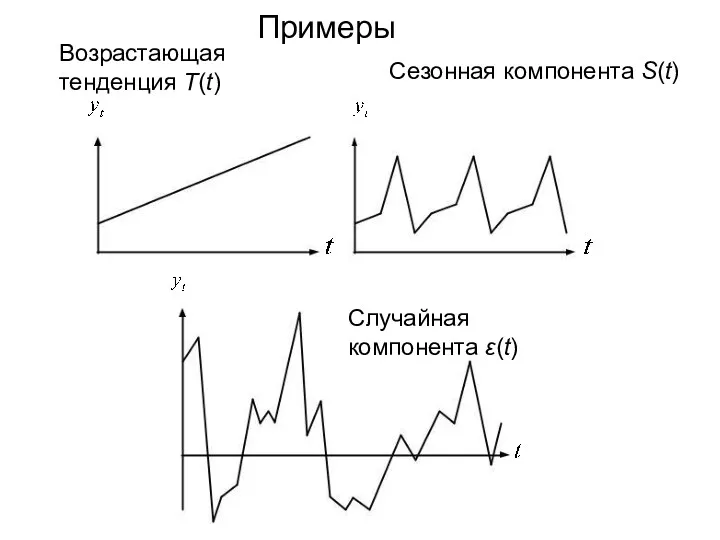
Примеры
Случайная компонента ε(t)
Сезонная компонента S(t)
Возрастающая тенденция T(t)

Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда.
Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда.

Стационарность ряда
Ряд называется слабо стационарным или просто стационарным, если средние, дисперсии и ковариации не зависят от времени t.

Стационарный случайный процесс
1.Математическое ожидание постоянно (стационарность в широком смысле).
2. Автокорреляционная функция зависит
только от разности аргумента.
В.Е. Гмурман. Теория вер. и мат. статистика. Стр. 386-449

Автокорреляция уровней временного ряда
Автокорреляция элементов временного ряда – корреляционная зависимость между последовательными элементами временного ряда.
Лаг – число периодов, по которым рассчитывается коэффициент автокорреляции между парами элементов ряда.
Автокорреляционная функция временного ряда – последовательность коэффициентов автокорреляции с лагами, равными 1, 2, 3 ….
Замечание. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции уменьшается. Для статистической достоверности используется правило: максимальный лаг не больше n/4.

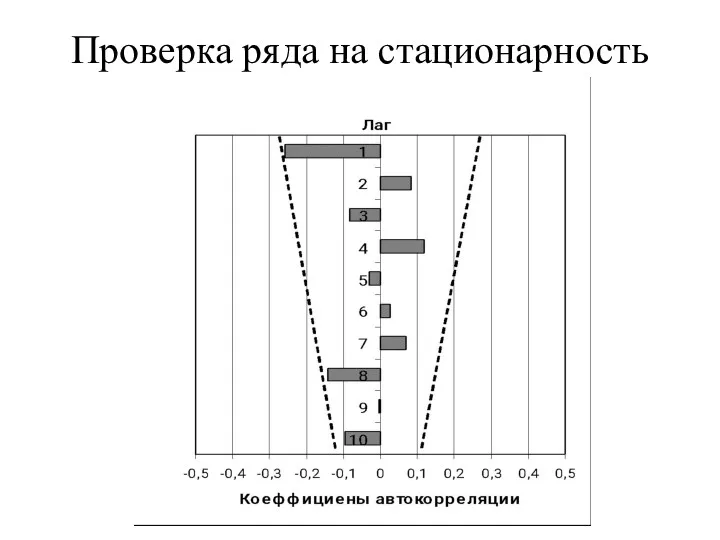
Проверка ряда на стационарность

Коэффициент автокорреляции остатков первого порядка определяется по формуле:
Критерий Дарбина-Уотсона и коэффициент автокорреляции остатков первого порядка связаны соотношением

Алгоритм выявления автокорреляции остатков на основе
критерия Дарбина-Уотсона:
1. Выдвигаются гипотезы:
Гипотеза H0 об отсутствии автокорреляции остатков.
Гипотеза H1 о наличии положительной автокорреляции в остатках.
Гипотеза H1* о наличии отрицательной автокорреляции в остатках.

2. По специальным таблицам определяются критические значения критерия Дарбина-Уотсона dL и dU для заданного числа наблюдений n (начиная со второго значения), числа независимых переменных k и уровня значимости α. По этим значениям числовой промежуток [0;4] разбивают на 5 отрезков.

Алгоритм проверки гипотезы о наличии автокорреляции остатков
2

Следующие тесты проверяют стационарность ряда. Это расширенный тест Дики–Фуллера (ADF). Еще один очень часто используемый тест, тест Филлипса–Перрона (PP). Оба теста проверяют нулевую гипотезу о нестационарности процесса при альтернативной гипотезе о том, что процесс стационарен. Тест Филлипса–Перрона учитывает возможность гетероскедастичности ошибок
Рассчитанная ADF-статистика сравнивается с N процентным (N=5%, 1%) уровнем значимости и на основе данного сравнения делается вывод о стационарности/нестационарности ряда.

ВЫЯВЛЕНИЕ СТРУКТУРЫ РЯДА:
Если наиболее высоким оказался коэффициент автокорреляции первого и/или второго порядка, исследуемый ряд содержит только тенденцию.
Если все коэффициенты автокорреляции оказались значимыми (высокими), то исследуемый ряд содержит только тенденцию.
Если наиболее высоким оказался коэффициент автокорреляции порядка t , ряд содержит циклические колебания с периодичностью в t моментов времени.

ОБНАРУЖЕНИЕ НЕСТАЦИОНАРНОСТИ
Визуальный анализ временного ряда. Возможно, временной ряд содержит видный на глаз временной тренд и сезонность (периодичную компоненту). Возможно, что разброс значений возрастает или убывает со временем (признак «случайного блуждания»). Это может служить указанием на зависимость среднего и, соответственно, дисперсии от времени. Во всех трех случаях ряд, скорее всего, не будет стационарным.

ИЗБАВЛЕНИЕ ОТ НЕСТАЦИОНАРНОСТИ
Выделить тренд и сезонность, т. е. неслучайную составляющую временного ряда.
Если ряд представляет «случайное блуждание», то взятие последовательных разностей делает ряд стационарным. На практике порядок разностей, как правило, не больше двух.

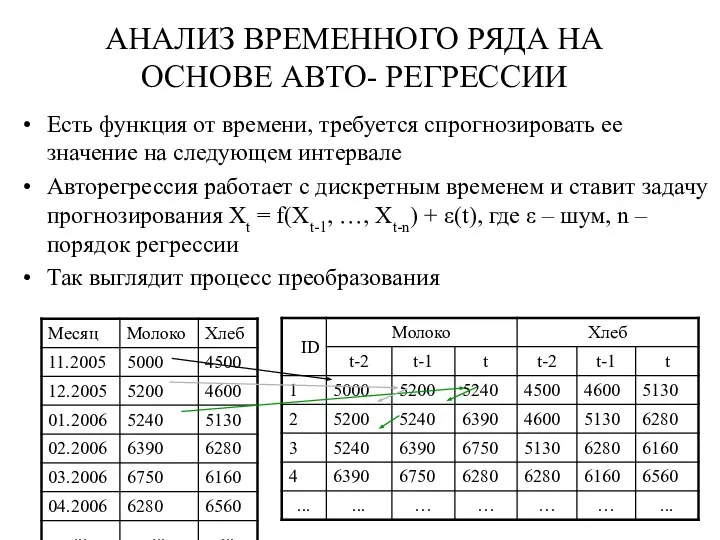
АНАЛИЗ ВРЕМЕННОГО РЯДА НА ОСНОВЕ АВТО- РЕГРЕССИИ
Есть функция от времени, требуется спрогнозировать ее значение на следующем интервале
Авторегрессия работает с дискретным временем и ставит задачу прогнозирования Xt = f(Xt-1, …, Xt-n) + ε(t), где ε – шум, n – порядок регрессии
Так выглядит процесс преобразования

АНАЛИЗ ВРЕМЕННОГО РЯДА
В случае линейной авторегрессии уравнение приобретает вид X(t) = a1X(t-1) + a2X(t-2) + ... + anX(t-n) + ε(t)
Для нахождения коэффициентов авторегрессии используется метод Юля – Уолкера (Yule – Walker, 1927 г.) минимизации среднеквадратичного отклонения между модельным и наблюдаемым временным рядом

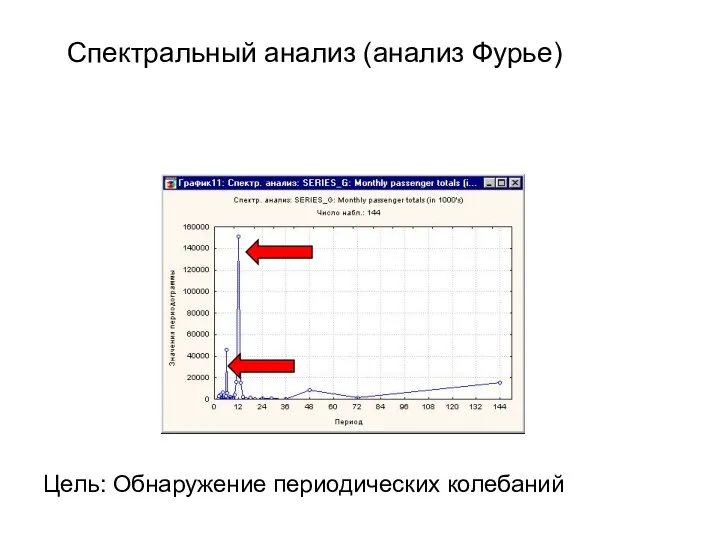
Спектральный анализ (анализ Фурье)
Цель: Обнаружение периодических колебаний

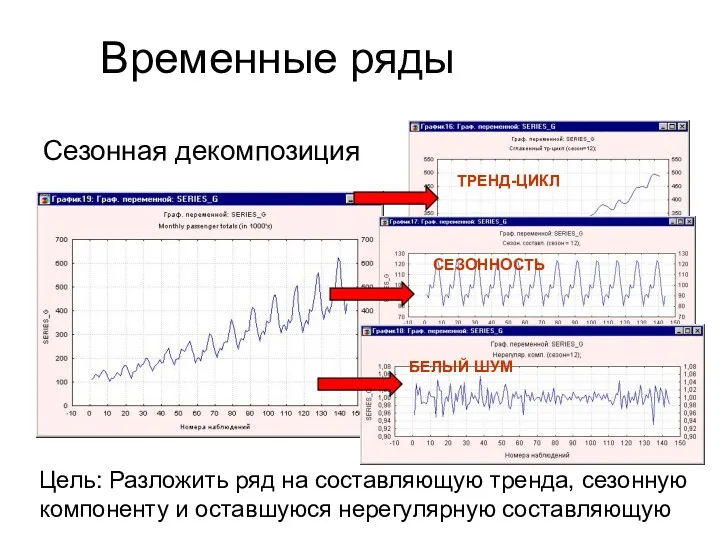
Временные ряды
Сезонная декомпозиция
Цель: Разложить ряд на составляющую тренда, сезонную
компоненту и оставшуюся нерегулярную составляющую
ТРЕНД-ЦИКЛ
СЕЗОННОСТЬ
БЕЛЫЙ ШУМ

Модели стационарных временных рядов
Модели Бокса-Дженкинса.
Модели авторегрессии и скользящего среднего ARMA(p,q)

ARMA(p,q)
процесс авторегрессии порядка p и скользящего среднего порядка q –ARMA(p,q)
авторегрессионный член порядка p
член скользящего среднего порядка q

Анализ стационарных временных рядов
Спецификация ARMA-моделей.
Оценивание модели.
Проверка адекватности модели.
Прогнозирование на основе построенной модели.

Спецификация ARMA-моделей.
Определение p и q.
Для этого можно построить графики автокорреляционной функции и частной автокорреляционной функции ряда для того, чтобы определить подходящие значения p и q. Автокорерляционные функции и частные автокорреляционные функции процессов AR(1), AR(2), MA(1), MA(2) и ARMA(1,1) легко опознать.

Спецификация ARMA-моделей (продолжение)
На этом этапе мы можем сформулировать несколько гипотез относительно возможных значениях порядков p и q. Для подходящих значений автокорреляционная функция остатков ARMA(p,q) – модели похожа на «белый шум».

Оценивание модели
В современные пакеты встроены различные методы оценивания ARIMA – моделей, такие как линейный или нелинейный МНК. полный или условный метод максимального правдоподобия.

Проверка адекватности модели
Необходимо проверить правильность предположений относительно параметров модели. Для этого
проверяем статистическую значимость коэффициентов модели должны достоверно отличатся от нуля
проверяем отсутствие автокорреляции в остатках ARMA(p,q) – модели

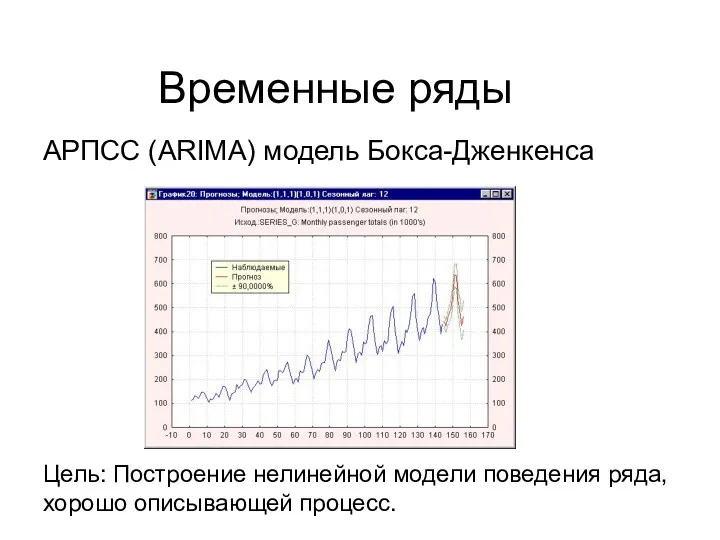
Временные ряды
АРПСС (ARIMA) модель Бокса-Дженкенса
Цель: Построение нелинейной модели поведения ряда,
хорошо описывающей процесс.

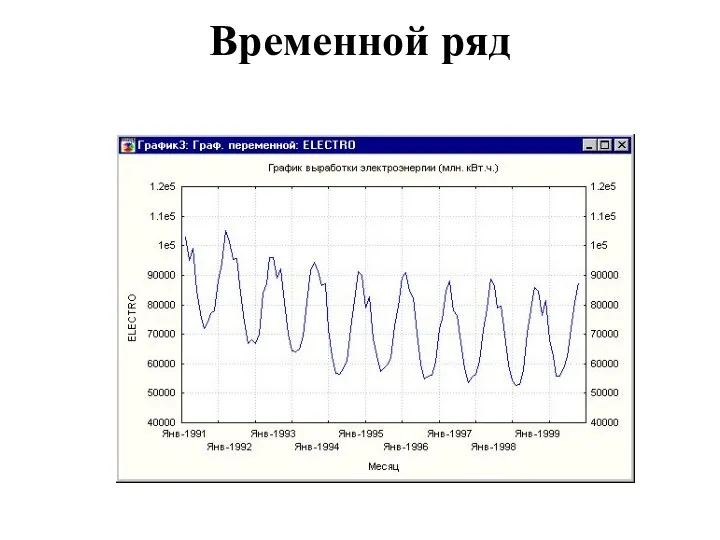
Временной ряд

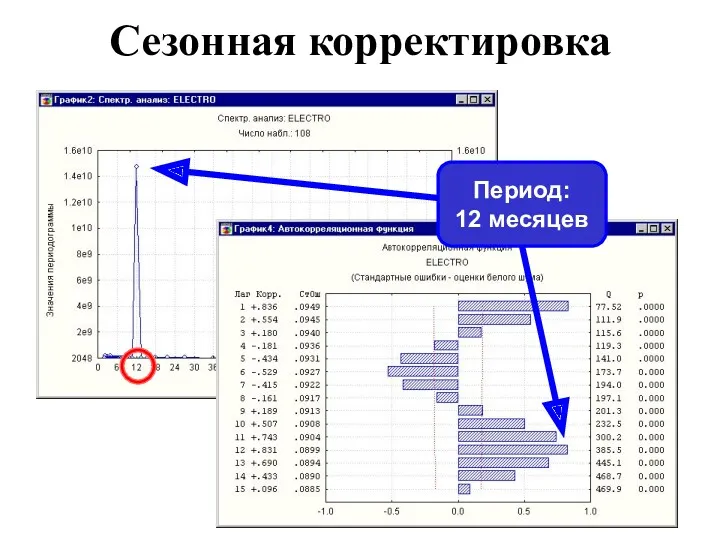
Сезонная корректировка
Период:
12 месяцев

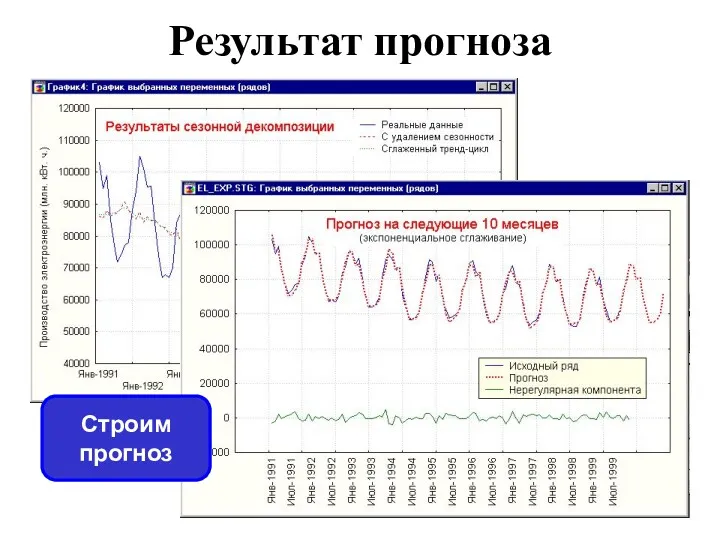
Результат прогноза
Строим
прогноз

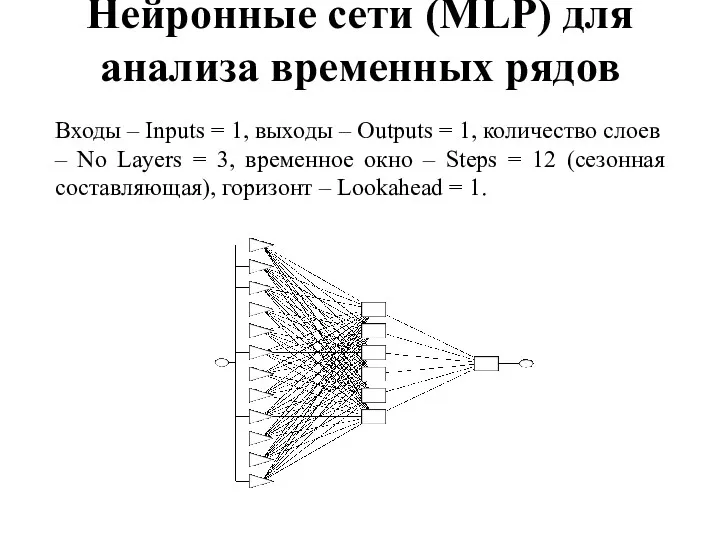
Нейронные сети (MLP) для анализа временных рядов
Входы – Inputs = 1, выходы – Outputs = 1, количество слоев – No Layers = 3, временное окно – Steps = 12 (сезонная составляющая), горизонт – Lookahead = 1.